научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 02, февраль 2012
УДК 519.6:681.51.011
МГТУ им. Н.Э. Баумана
Введение
При расчете систем автоматического управления для достижения наибольшей эффективности систем – минимума перерегулирования, минимальной длительности переходного процесса, минимума ошибки – возникает задача оптимизации, в частности, численной. Для таких задач имеется развитый математический аппарат [1-4] и различные программные среды, одна из которых – MatLab – популярна для математиков и инженеров. Если целевую функцию можно записать в явном формульном виде, как правило, никаких особых проблем при ее оптимизации не возникает – пользуются встроенными средствами MatLab, т.е. встроенной функцией fminsearchили встроенным пакетом с итерактивной оптимизацией OptimizationToolbox. Задача усложняется, если записать целевую функцию аналитически нельзя. Это имеет место, например, когда значение целевой функции определяется только численными методами и никак не подсчитывается аналитически. Такое происходит, в частности, когда моделируется переходный процесс в автоматической системе: параметры переходного процесса станут известны только после выполнения очередного акта имитационного моделирования. В таких случаях необходимо вручную писать на языке MatLabпрограмму, реализующую какой-либо алгоритм численной оптимизации.
Структура программного комплекса
Разработан комплекс таких программ, автоматизирована оптимизация переходного процесса. Для имитационного моделирования процесса используется встроенное средство моделирования систем – Simulink. После каждой реализации моделирования выходные данные передаются в рабочее пространство MatLab, где обрабатываются написанными программами (рис. 1).
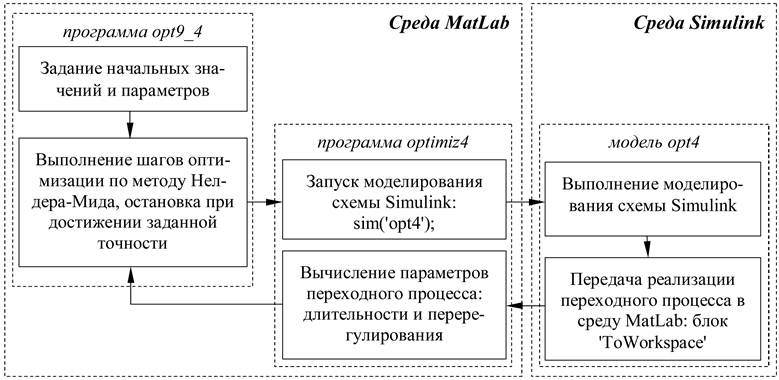
Рис. 1. Структура взаимодействия программ для оптимизации переходного процесса
Проводился сравнительный анализ методов численной оптимизации, в результате которого был выбран метод деформируемого многогранника. Также его называют симплекс-методом, методом Нелдера-Мида [1-6]. Специалисты характеризуют данный метод как один из самых эффективных и удобных для выполнения на ЭВМ. Его преимущество перед случайным поиском – существенно меньшее количество вычислений целевой функции. Как показал сравнительный анализ, меньшее в 3-4 раза и более того, в зависимости от конкретной задачи. Преимущество перед градиентными методами – отсутствие ограничений на вид целевой функции. Можно заметить, что встроенная функция MatLabfminsearchпо умолчанию использует именно метод Нелдера-Мида. Также особенностью является расширяемость программного комплекса, разработанного в пакете MatLab: если понадобится оптимизировать другую систему или изменить критерий оптимизации, требуемые модификации программ будут незначительными. Написанные программы достаточно объемны, приводятся в работе [6]. Взаимосвязь между программами показана на рис. 1.
Пример оптимизации
Для примера рассмотрим САУ, структурная схема которой приведена на рис. 2. Требуется подобрать такие параметры корректирующих звеньев ![]() ,
, ![]() и
и ![]() , чтобы при начальном рассогласовании
, чтобы при начальном рассогласовании ![]() рад перерегулирование не превышало 0,3 рад, а время переходного (время входа в трубку
рад перерегулирование не превышало 0,3 рад, а время переходного (время входа в трубку ![]() рад) не превышало 2 с.
рад) не превышало 2 с.

Рис. 2. Структурная схема САУ
Для проведения оптимизации необходимо задать начальные значения изменяемых параметров. Можно выбрать их наугад, но лучше воспользоваться для выбора какой-либо определенной закономерностью. Рассматривалось и использовалось два способа.
Первый заключается в построении ЛЧХ разомкнутой системы и ее последующей модификации за счет изменения параметров системы. Параметры подбирают, исходя из заданной динамической ошибки и необходимых запасов устойчивости, согласно теории частотного синтеза САУ [5-7].
Линеаризуем систему, убрав нелинейные блоки, и размыкаем главную обратную связь в точке измерения ошибки. Положим ![]() ,
, ![]() и
и ![]() . Рассчитанные характеристики приведены на рис. 3. Видно, что АЧХ весьма опущена. Это плохо тем, что при динамическом изменении
. Рассчитанные характеристики приведены на рис. 3. Видно, что АЧХ весьма опущена. Это плохо тем, что при динамическом изменении ![]() ошибка
ошибка ![]() будет велика, особенно на высоких частотах. АЧХ можно поднять, увеличив
будет велика, особенно на высоких частотах. АЧХ можно поднять, увеличив ![]() и уменьшив
и уменьшив ![]() на несколько порядков. Например, если изменяем только
на несколько порядков. Например, если изменяем только ![]() и требуем, чтобы частота среза равнялась 1 Гц,
и требуем, чтобы частота среза равнялась 1 Гц, ![]() следует увеличить на 68,3 дБ, или
следует увеличить на 68,3 дБ, или ![]() (рис. 3). При таком большом коэффициенте усиления система становится неустойчивой – присутствует ярко выраженная резонансная частота, генерируются гармонические колебания. Исходя из соображений устойчивости и уменьшения динамической ошибки, примем начальные значения для оптимизации:
(рис. 3). При таком большом коэффициенте усиления система становится неустойчивой – присутствует ярко выраженная резонансная частота, генерируются гармонические колебания. Исходя из соображений устойчивости и уменьшения динамической ошибки, примем начальные значения для оптимизации: ![]() ,
, ![]() ,
, ![]() . При этом частота среза составляет 0,6 Гц, запас по фазе 45о, запас по амплитуде 4,3 дБ (рис. 3).
. При этом частота среза составляет 0,6 Гц, запас по фазе 45о, запас по амплитуде 4,3 дБ (рис. 3).

Рис. 3. Логарифмические частотные характеристики следящей системы,
1 – исходной и 2 – скорректированной, ![]() – амплитудные,
– амплитудные, ![]() – фазовые
– фазовые
Второй подход состоит в наблюдении изменения переходного процесса системы при заданном изменении определенного параметра. Написана соответствующая программа, процесс наблюдения интерактивный. Это своего рода одномерная оптимизация «вручную» с равномерным поиском. Какой переходный процесс из всех наблюдаемых оказался качественнее, то значение параметра и принимают за лучшее (рис. 4). Затем можно исследовать другой параметр. Таким способом выясняется чувствительность системы к изменению параметра. Не исключено, что какой-либо из них на характеристики системы практически не влияет, и оптимизировать по нему бессмысленно. В нашем примере все три параметра оказались влияющими.
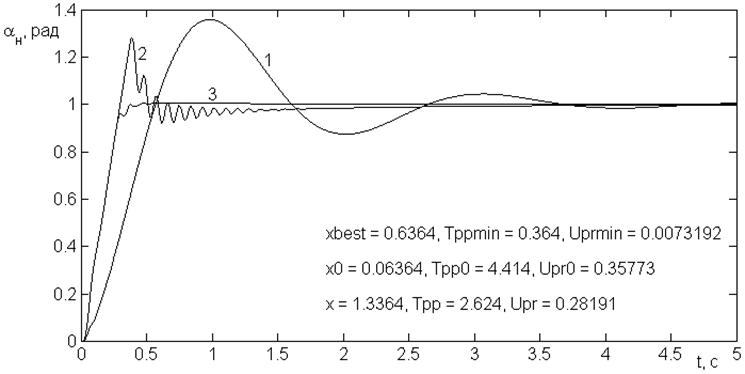
Рис. 4. Влияние параметра ![]() на переходный процесс:
на переходный процесс:
1 – ![]() с, 2 –
с, 2 – ![]() с, 3 –
с, 3 – ![]() с –наименьшие длительность и перерегулирование
с –наименьшие длительность и перерегулирование
Выбрав начальные значения, можно запускать непосредственную оптимизацию. Стоит заметить, скорее всего целевая функция окажется многомодальной. Чтобы надежнее найти глобальный минимум, надо задавать разные начальные значения и повторно проводить процесс. Как вариант, полученные в предыдущем акте оптимизации наилучшие значения использовать в качестве начальных для следующего акта.
Результаты оптимизации приведены на рис. 5. Как показало моделирование, перерегулирование ![]() и длительность переходного процесса
и длительность переходного процесса ![]() зависимы: при уменьшении
зависимы: при уменьшении ![]() как правило уменьшается и
как правило уменьшается и ![]() . При уменьшении
. При уменьшении ![]() не всегда уменьшается
не всегда уменьшается ![]() . В связи с этим минимизируемому
. В связи с этим минимизируемому ![]() был дан больший вес. Оптимизируемая величина yвычислялась по формуле:
был дан больший вес. Оптимизируемая величина yвычислялась по формуле:
![]() ,
,
где ![]() и
и ![]() – соответствующие весовые коэффициенты. В нашем случае принято:
– соответствующие весовые коэффициенты. В нашем случае принято: ![]() ,
, ![]() .
.
В ходе оптимизации получили значения: ![]() ,
, ![]() и
и ![]() с. При этом минимизируемые величины имеют значения: время переходного процесса
с. При этом минимизируемые величины имеют значения: время переходного процесса ![]() с и перерегулирование
с и перерегулирование ![]() рад. Как видно на рис. 4, длительность переходного процесса уменьшилась почти в пять раз при том, что перерегулирование практически свелось к нулю.
рад. Как видно на рис. 4, длительность переходного процесса уменьшилась почти в пять раз при том, что перерегулирование практически свелось к нулю.

Рис. 5. Результаты оптимизации: 1 – переходный процесс до оптимизации, 2 – после
Заключение
На данном примере демонстрируется оптимизация САУ на основе разработанного программного комплекса. Видно, что оптимизация достаточно эффективна: переходный процесс значительно улучшается согласно заданному критерию. Однако важно заметить, что в случае сложных САУ и многопараметрической оптимизации требуется тщательный подход. В частности, следует многократно искать решение для разных начальных значений параметров. В перспективе можно будет выработать определенные рекомендации для таких случаев. А также перенести комлекс со среды MatLabв другую программную среду. Поскольку хоть среда MatLabуниверсальна, но производительность вычислений у нее низка, и в случае сложных САУ оптимизация может выполняться долго.
Список литературы
1. Химмельблау Д. Прикладное нелинейное программирование: Пер. с англ. М. : Мир, 1975.
2. Методы оптимизации / Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. – М. : Глав. ред. физ.-мат. лит. изд-ва «Наука», 1978.
3. Методы оптимизации в примерах и задачах: Учеб. пособие / А.В. Пантелеев, Т.А. Летова. – 2-ое изд., исправл. – М.: Высш. шк., 2005.
4. Мэтьюз Джон Г., Финк Куртис Д. Численные методы. Использование MatLab. 3-е изд.: Пер. с англ. М. : Издательский дом «Вильямс», 2001.
5. Крутько П.Д., Максимов А.И., Скворцов Л.М. Алгоритмы и программы проектирования автоматических систем / под ред. П.Д. Крутько. М. : Радио и связь, 1988.
6. Максимов А.И., Аливер В.Ю. Численные методы в задачах проектирования автоматических систем. Ч. 2: учебное пособие – М. : Изд-во МГТУ им. Н. Э. Баумана, 2011.
7. Попов Е.П. Теория линейных систем автоматического регулирования и управления – М. : Глав. ред. физ.-мат. лит. изд-ва «Наука», 1978.
8. Кулешов В.С., Лакота Н.А. Динамика систем управления манипуляторами – М. : Энергия, 1971.
Публикации с ключевыми словами: MATLAB, методы оптимизации, численная оптимизация, системы автоматического регулирования, переходный процесс, перерегулирование
Публикации со словами: MATLAB, методы оптимизации, численная оптимизация, системы автоматического регулирования, переходный процесс, перерегулирование
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



