научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2011
МГТУ им. Н.Э. Баумана
- Введение.
Одна из основных проблем строительства в криолитозоне (на Дальнем Севере) состоит в том, что таяние вечномерзлого грунта, в результате теплового воздействия со стороны установленного на нем отапливаемого здания, ведет к проявлению опасных криогенных процессов и, в результате, к аварийной ситуации. К опасным криогенным процессам относятся, прежде всего, следующие процессы [1].
Пучение грунта – увеличение объёма грунта, в результате его промерзания. Неравномерное поднятие поверхности грунта при пучении ведет к повреждениям построенного на поверхности грунта здания (сооружения).
Осадка – уменьшение объема грунта деятельного слоя (т.е. верхнего слоя грунта, подверженного процессам сезонного промерзания и оттаивания), потеря им прочностных свойств и рост сжимаемости при оттаивании. Неравномерная деформация грунта при оттаивании ведет к повреждениям построенного на его поверхности сооружения.
Периодический процесс пучения и осадки, связанный с сезонным промерзанием и оттаиванием грунта, постепенно разрушает здание. При промерзании грунт смерзается с поверхностью фундамента, а затем при пучении деформирует ее. Это может привести к перемещению фундамента. В дальнейшем, при оттаивании грунт теряет свои прочностные свойства, существенно возрастает его сжимаемость (возникают просадки). Возможен также выпор такого грунта из-под подошвы фундамента.
Наледь – ледяное образование под зданием. В результате теплового воздействия здания на грунт, под зданием глубина промерзания значительно меньше, чем на открытой поверхности земли. Вследствие этого, возникают напорные воды, которые могут прорываться, и, вытекая через двери и окна здания, замерзая на поверхности земли, содавать наледь.
При резком замерзании грунта, в нем образуются морозобойные трещины – трещины шириной порядка 10-15 см, рассекающие поверхность грунта и уходящие на несколько метров в глубину. Со временем в такие трещины попадает вода, а ее замерзание приводит к их росту.
Просадка – сокращение объема вечномерзлого грунта (т.е. глубинного слоя грунта, находящегося под деятельным слоем и не подверженного процессам сезонного промерзания и оттаивания), потеря им прочностных свойств и рост сжимаемости в результате его оттаивания. Неравномерная деформация многолетнемерзлого грунта при оттаивании ведет к повреждениям установленного на его поверхности здания.
В случае, если здание установлено на склоне, возможно явление солифлюкции. Солифлюкция – это течение склона, вызванное его периодическим промерзанием и оттаиванием. Для пояснения рассмотрим произвольную фиксированную точку на поверхности склона. В результате замерзания и, соответственно, пучения грунта, эта точка перемещается вдоль вектора перпендикулярного поверхности склона. При дальнейшем таянии грунта, она, под действием силы тяжести, перемещается вертикально вниз и, в результате оказывается ниже по склону, чем была в начальный момент времени.
Очевидно, что все перечисленные опасные криогенные процессы, оказывающие разрушительное влияние на здание, связаны с замерзанием и оттаиванием грунта под зданием и определяются динамикой температурного поля грунта. Поэтому температура грунта под зданием является основным фактором, определяющим его прочность и устойчивость. В настоящей работе моделировалась динамика температурного поля грунтов основания здания, установленного полами по грунту в условиях сплошной мерзлоты в районах с сезонными промерзаниями и оттаиваниями почвы. Результаты моделирования позволяют анализировать опасные воздействия здания на грунт.
2. Постановка задачи
Рассмотрим здание, установленное непосредственно на поверхность грунта (без фундамента) и поставим задачу моделирования динамики температурного поля в прямоугольной области грунта под зданием, которую назовем расчетной областью. Будем считать, что здание отапливается и внутри него поддерживается постоянная температура (например, ![]() ). На рис.1 представлена часть расчетной области
). На рис.1 представлена часть расчетной области ![]()
![]() ,
, ![]() (прямоугольный параллелепипед), соответствующая первой координатной четверти (
(прямоугольный параллелепипед), соответствующая первой координатной четверти (![]() ). Плоскость
). Плоскость ![]() отвечает поверхности земли. Ось
отвечает поверхности земли. Ось ![]() направлена вглубь грунта. Закрашенный прямоугольник на верхней границе обасти соответствует зданию, расположенному над этой областью. Предполагается симметрия здания, состава грунта и пр. относительно координатных плоскостей xOzи yOz, поэтому моделирование динамики температурного поля достаточно провести в рассматриваемой четверти расчетной области. Область
направлена вглубь грунта. Закрашенный прямоугольник на верхней границе обасти соответствует зданию, расположенному над этой областью. Предполагается симметрия здания, состава грунта и пр. относительно координатных плоскостей xOzи yOz, поэтому моделирование динамики температурного поля достаточно провести в рассматриваемой четверти расчетной области. Область ![]() неоднородна и состоит из нескольких литологических слоев, т.е. областей грунта с различным составом и, как следствие, с различными физическими характеристиками. К физическим характеристикам литологических слоев относятся следующие величины:
неоднородна и состоит из нескольких литологических слоев, т.е. областей грунта с различным составом и, как следствие, с различными физическими характеристиками. К физическим характеристикам литологических слоев относятся следующие величины:
![]() – плотность сухого грунта,
– плотность сухого грунта,
![]() – удельная теплоемкость сухого грунта,
– удельная теплоемкость сухого грунта,
![]() – суммарная влажность грунта в долях к массе сухого грунта,
– суммарная влажность грунта в долях к массе сухого грунта,
![]() – коэффициент теплопроводности мерзлого грунта,
– коэффициент теплопроводности мерзлого грунта,
![]() – коэффициент теплопроводности талого грунта,
– коэффициент теплопроводности талого грунта,
![]() – доля незамерзшей воды по отношению к массе сухого грунта (см. ниже).
– доля незамерзшей воды по отношению к массе сухого грунта (см. ниже).
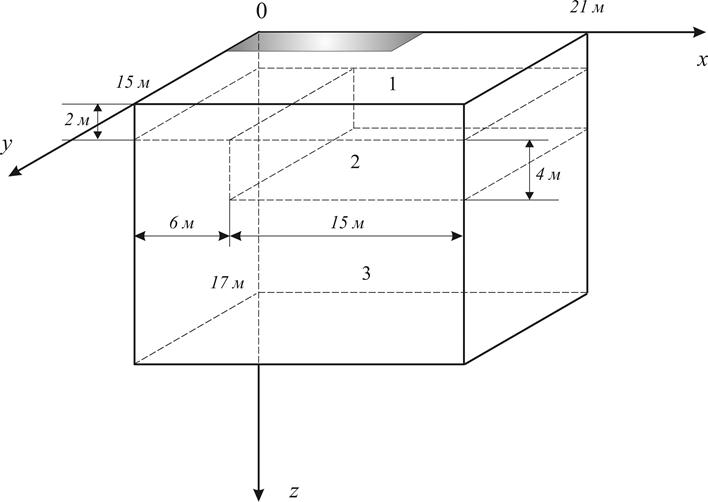
Рис. 1. Расчетная область
Для примера, на рис. 1 выделено 3 литологических слоя: ![]() ,
, ![]() и
и ![]() (соответственно, области 1, 2 и 3 на рис. 1), Принадлежность точки
(соответственно, области 1, 2 и 3 на рис. 1), Принадлежность точки ![]() , соответствующей области
, соответствующей области ![]() определяется следующими формулами:
определяется следующими формулами:
![]() ,
,
![]() , (1)
, (1)
![]() .
.
Верхняя граница области D(z=0) тоже, вообще говоря, не является однородной. Так, в качестве примера, на рис. 2 она разбита на три зоны: 1, 2 и 3. В зоне 2 (заполненный текстурой «кирпичная стена» прямоугольник) располагается здание. Зона 1 – зона прямого контакта грунта с атмосферой (отсутствие снежного покрова или тонкий снежный покров). Зона 3 – зона снежных надувов (сугробы).

Рис. 2. Верхняя граница расчетной области
Динамика температурного поля ![]() в области D, с учетом фазовых переходов – твердое тело-жидкость, описывается уравнением теплопроводности в виде
в области D, с учетом фазовых переходов – твердое тело-жидкость, описывается уравнением теплопроводности в виде
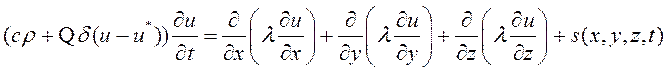 , (2)
, (2)
где ![]() – удельная теплоемкость;
– удельная теплоемкость;
![]() – плотность;
– плотность;
![]() – коэффициент теплопроводности;
– коэффициент теплопроводности;
![]() – температура среды;
– температура среды;
![]() – температура фазового перехода (отметим, что температура начала замерзания грунта, вообще говоря, чуть ниже нуля и зависит от разновидности грунта и концентрации порового раствора в нем[2],но здесь приближенно принимается
– температура фазового перехода (отметим, что температура начала замерзания грунта, вообще говоря, чуть ниже нуля и зависит от разновидности грунта и концентрации порового раствора в нем[2],но здесь приближенно принимается ![]() 0 °С);
0 °С);
![]() – теплота фазового перехода;
– теплота фазового перехода;
![]() – дельта-функция.
– дельта-функция.
![]() – мощность внутренних источников тепла.
– мощность внутренних источников тепла.
Внутренние источники тепла в задаче отсутствуют, поэтому![]() .
.
Начальное условие зададим, фиксировав распределение температуры в грунте в момент времени t=0 (на практике, такое распределение может быть найдено по результатам геотехнического мониторинга):
![]() . (3)
. (3)
Граничные условия зададим следующим образом. На границе ![]() с температурой
с температурой ![]() происходит конвективный теплообмен со средой, имеющей температуру
происходит конвективный теплообмен со средой, имеющей температуру ![]() . Плотность теплового потока
. Плотность теплового потока ![]() на этой границе задается через коэффициент теплоотдачи
на этой границе задается через коэффициент теплоотдачи ![]() в виде
в виде
![]() . (4)
. (4)
На границе ![]() поддерживается постоянная температура, равная температуре окружающей среды, имеющей температуру
поддерживается постоянная температура, равная температуре окружающей среды, имеющей температуру
![]() . (5)
. (5)
Боковые границы области ![]() теплоизолированы
теплоизолированы
 ,
,  ,
,
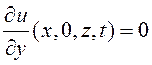 ,
,  . (6)
. (6)
Слагаемое ![]() в левой части уравнения (2) можно написать в следующем виде:
в левой части уравнения (2) можно написать в следующем виде:

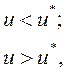 (7)
(7)
где![]() =0.49 ккал/(кг·оС) и
=0.49 ккал/(кг·оС) и ![]() =1.006 ккал/(кг·оС) – удельные теплоемкости льда и воды, соответственно,
=1.006 ккал/(кг·оС) – удельные теплоемкости льда и воды, соответственно, ![]() ккал/кг – удельная теплота фазового перехода льда. Формула для объемной теплоемкости (7) учитывает фазовые переходы в области отрицательных температур. Функцией
ккал/кг – удельная теплота фазового перехода льда. Формула для объемной теплоемкости (7) учитывает фазовые переходы в области отрицательных температур. Функцией ![]() описывается массовая доля (по отношению к массе сухого грунта) незамершей воды при температуре
описывается массовая доля (по отношению к массе сухого грунта) незамершей воды при температуре ![]() .
.
Вследствие вышесказанного плотность влажного грунта ![]() представляется выражением
представляется выражением
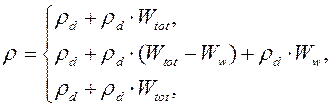
 (8)
(8)
где ![]()
![]() температура замерзания грунтовой воды; т.е. при
температура замерзания грунтовой воды; т.е. при ![]() вся влага находится в твердом состоянии (лед), при
вся влага находится в твердом состоянии (лед), при ![]() вся влага находится в жидком состоянии (вода); при
вся влага находится в жидком состоянии (вода); при ![]() часть влаги (
часть влаги (![]() ) находится в жидком состоянии, а часть влаги
) находится в жидком состоянии, а часть влаги ![]()
![]() в твердом состоянии.
в твердом состоянии.
Зависимость ![]() описывается интерполяционной формулой [3]
описывается интерполяционной формулой [3]
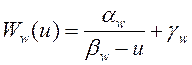 , (9)
, (9)
где постоянные коэффициенты ![]() и
и ![]() свои для каждого литологического слоя грунта и определяются по трем значениям функции
свои для каждого литологического слоя грунта и определяются по трем значениям функции ![]() при трех различных значениях температуры
при трех различных значениях температуры ![]() . Рис.3 иллюстрирует зависимости
. Рис.3 иллюстрирует зависимости ![]() от температуры. Кривые 1 и 2 соответствуют двум различным литологическим слоям.
от температуры. Кривые 1 и 2 соответствуют двум различным литологическим слоям.
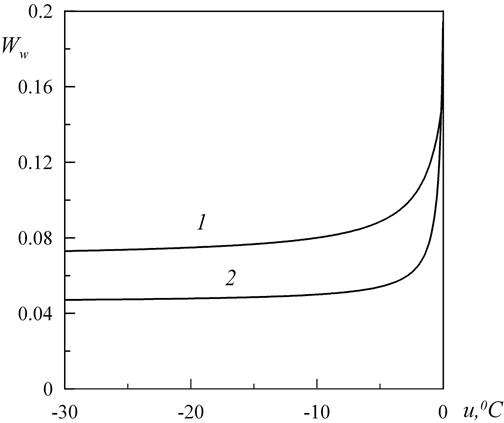
Рис. 3. Кривые незамершей воды
Коэффициент теплопроводности ![]() в уравнении (2) определяется так
в уравнении (2) определяется так

 (10)
(10)
Коэффициент теплоотдачи ![]() в формуле (4) записывается в виде
в формуле (4) записывается в виде
 , (11)
, (11)
где ![]() – коэффициент конвективного теплообмена,
– коэффициент конвективного теплообмена, ![]() – термическое сопротивление [3].
– термическое сопротивление [3].
Теплота фазового перехода ![]() при
при ![]() вычисляется по формуле [2]
вычисляется по формуле [2] ![]() .
.
3. Решение задачи методом контрольного объема
Краевая задача (2) – (6) решалась численно. Прежде всего, коэффициент в левой части уравнения (2) сглаживается и совершается переход к обычной задаче теплопроводности [4]. Дельта-функция ![]() заменяется некоторой функцией
заменяется некоторой функцией ![]() , которая отлична от нуля лишь внутри некоторого промежутка сглаживания
, которая отлична от нуля лишь внутри некоторого промежутка сглаживания ![]() . В результате вместо решения (2) ищется решение уравнения со сглаженным коэффициентом
. В результате вместо решения (2) ищется решение уравнения со сглаженным коэффициентом
 (12)
(12)
Для аппроксимации дельта-функции используются различные формулы, которые строятся с учетом выполнения условия сохранения теплового баланса на отрезке ![]() . В настоящей работе используются следующие формулы [4]:
. В настоящей работе используются следующие формулы [4]:
ступенчатая аппроксимация

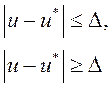 (13)
(13)
и параболическая аппроксимация
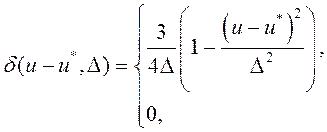
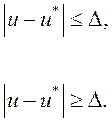 (14)
(14)
Можно убедиться в том, что для обеих формул (13) и (14) выполняется условие
 .
.
Параметр ![]() влияет на результаты расчетов, он зависит от используемой расчетной сетки и, как правило, определяется опытным путем в результате методических расчетов.
влияет на результаты расчетов, он зависит от используемой расчетной сетки и, как правило, определяется опытным путем в результате методических расчетов.
Задача теплопроводности ((12), (3) – (6)) решалась методом контрольного объема. Суть метода изложена ниже. В начале, для простоты изложения, рассматривается одномерная задача. Потом проводится обобщение на трехмерный случай. В качестве примера рассмотрим следующую задачу: найти численное решение ![]() уравнения теплопроводности
уравнения теплопроводности
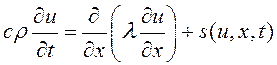 (15)
(15)
в ограниченной области ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию
![]() (16)
(16)
и граничным условиям
![]() ,
,
![]() , (17)
, (17)
где ![]() – температура среды,
– температура среды, ![]() – мощность внутренних источников тепла,
– мощность внутренних источников тепла, ![]() ,
, ![]() и
и ![]() – заданные функции.
– заданные функции.
Разобьем отрезок![]() на m участков, которые назовем контрольными объемами (КО) (рис.4а). Точки сетки
на m участков, которые назовем контрольными объемами (КО) (рис.4а). Точки сетки
![]() =
=![]() (18)
(18)
определяют границы КО; индекс левой границы КО соответствует его номеру: 1-ый, 2-ой, …, m-ый контрольные объемы (КО); ![]() ,
, ![]() -
- ![]() ый шаг сетки
ый шаг сетки ![]() или ширина
или ширина ![]() ого КО (в общем случае сетка предполагается неравномерной). Точки области
ого КО (в общем случае сетка предполагается неравномерной). Точки области ![]() , в которых будем искать решение задачи, назовем расчетными. В качестве внутренних расчетных точек выберем центры КО:
, в которых будем искать решение задачи, назовем расчетными. В качестве внутренних расчетных точек выберем центры КО: ![]() , i=1,…,m+1; добавим к этим точкам две граничные точки
, i=1,…,m+1; добавим к этим точкам две граничные точки![]() и
и ![]() , и назовем сеткой
, и назовем сеткой ![]() объединенное множество внутренних и граничных расчетных точек –
объединенное множество внутренних и граничных расчетных точек – ![]() (рис. 4б).
(рис. 4б).
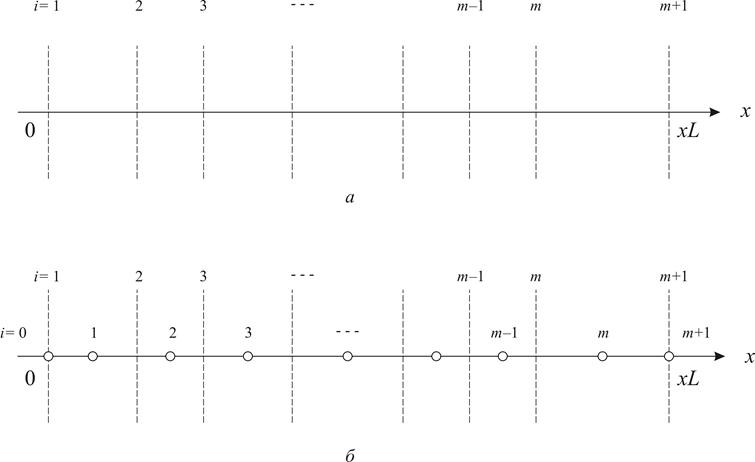
Рис. 4. Построение расчетной сетки
Фрагмент расчетной сетки ![]() , показан на рис. 5. Точки сетки обозначены заглавными буквами W, Р и Е: Р — рассматриваемая точка (Point), а Е и W – соответственно «восточная» (East) и «западная» (West) соседние с ней точки [5,6]. В скобках указаны индексы расчетных точек –
, показан на рис. 5. Точки сетки обозначены заглавными буквами W, Р и Е: Р — рассматриваемая точка (Point), а Е и W – соответственно «восточная» (East) и «западная» (West) соседние с ней точки [5,6]. В скобках указаны индексы расчетных точек – ![]() ,
, ![]() и
и ![]() , соответственно. Штриховыми линиями показаны грани КО. Для обозначения граней КО, содержащего точку Р, используются буквы
, соответственно. Штриховыми линиями показаны грани КО. Для обозначения граней КО, содержащего точку Р, используются буквы ![]() и
и ![]() . Расстояние между точками W и Р обозначим как
. Расстояние между точками W и Р обозначим как ![]() , а между точками Р и Е – как
, а между точками Р и Е – как ![]() . Ширину контрольного объема обозначим через
. Ширину контрольного объема обозначим через ![]() .
.

Рис. 5. Фрагмент расчетной сетки
Запишем уравнение (15) в виде
 . (19)
. (19)
Здесь
 (20)
(20)
– плотность теплового потока.
Проинтегрируем обе части равенства (19) по КО, содержащему точку ![]() , т.е. от
, т.е. от ![]() до
до ![]() :
:
 .
.
В результате получим
 , (21)
, (21)
где ![]() – известное значение температуры
– известное значение температуры ![]() в точке
в точке ![]() в момент времени
в момент времени ![]() ,
, ![]() – соответствует неизвестной температуре в точке
– соответствует неизвестной температуре в точке ![]() в момент времени
в момент времени ![]() ,
, ![]() . При интегрировании температуру внутри КО считаем постоянной и равной температуре
. При интегрировании температуру внутри КО считаем постоянной и равной температуре ![]() . Первые два слагаемых в правой части уравнения (21) отвечают плотностям входящего и выходящего потоков тепла, интеграл выражает суммарную мощность генерации тепла в КО.
. Первые два слагаемых в правой части уравнения (21) отвечают плотностям входящего и выходящего потоков тепла, интеграл выражает суммарную мощность генерации тепла в КО.
Для выражения ![]() и
и ![]() через температуры в расчетных точках используем кусочно-линейный профиль, изображенный штрихпунктирной линией на рис.5б. В результате получим
через температуры в расчетных точках используем кусочно-линейный профиль, изображенный штрихпунктирной линией на рис.5б. В результате получим

 . (22)
. (22)
Обозначим среднюю мощность генерации тепла в КО через ![]() . Линеаризуем
. Линеаризуем ![]() по температуре:
по температуре: ![]() . Тогда
. Тогда
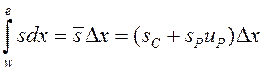 . (23)
. (23)
В случае, когда ![]() не зависит от температуры, имеем
не зависит от температуры, имеем ![]() ,
, ![]() .
.
Подставив (22) и (23) в выражение (21), получим дискретный аналог уравнения (19) в виде
![]() , (24)
, (24)
где
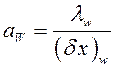 ,
, 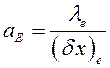 ,
,  ,
,
![]() ,
, ![]() .
.
При аппроксимации плотности теплового потока по формулам (22) используются значения коэффициента теплопроводности ![]() на гранях КО. В задаче же все необходимые величины задаются в расчетных точках – центрах КО. Если теплопроводность задана только в расчетной точке, то разумно предположить, что ее значение остается постоянным по всему КО, окружающему эту точку. Другими словами, каждый КО заполнен материалом с постоянной теплопроводностью (соответствующей ее значению в расчетной точке).
на гранях КО. В задаче же все необходимые величины задаются в расчетных точках – центрах КО. Если теплопроводность задана только в расчетной точке, то разумно предположить, что ее значение остается постоянным по всему КО, окружающему эту точку. Другими словами, каждый КО заполнен материалом с постоянной теплопроводностью (соответствующей ее значению в расчетной точке).
Если зависимость температуры от ![]() аппроксимировать кусочно-линейным профилем, изображенным на рис.5,б сплошной линией, то плотность теплового потока на грани
аппроксимировать кусочно-линейным профилем, изображенным на рис.5,б сплошной линией, то плотность теплового потока на грани ![]() может быть найдена по следующей формуле
может быть найдена по следующей формуле
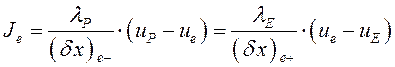 (25)
(25)
Исключив ![]() из этого выражения, получим
из этого выражения, получим
 (26)
(26)
Сравнивая вторую формулу в (22) с (26), запишем выражение для коэффициента ![]()
 (27)
(27)
Аналогично записывается формула для коэффициента ![]()
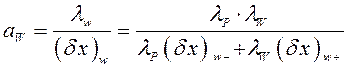 (28)
(28)
Из (25) можно также вывести формулу для ![]() :
:
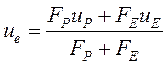 , (29)
, (29)
где  ,
,  .
.
В вычислительной схеме мы получаем температуры в расчетных точках и обычно не определяем температуры на гранях контрольных объемов. Когда необходимо получить температуру на грани, нужно использовать выражение (29).
Формула (28) используется для вычисления ![]() , когда индекс
, когда индекс ![]() точки P принимает значения от 2 до
точки P принимает значения от 2 до ![]() , а формула (27) – для
, а формула (27) – для ![]() . При
. При ![]() левая грань первого КО совпадает с точкой
левая грань первого КО совпадает с точкой ![]() , поэтому полагая
, поэтому полагая ![]() , получаем для
, получаем для ![]() выражение
выражение
 (30)
(30)
На правой границе области при ![]() правая грань
правая грань ![]() ого КО совпадает с точкой
ого КО совпадает с точкой ![]() , т.е. здесь
, т.е. здесь ![]() . Для коэффициента
. Для коэффициента ![]() получается формула
получается формула
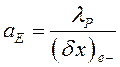 (31)
(31)
Введем новые обозначения для коэффициентов в уравнении (24):
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
С учетом построенной сетки (см. формулу (18) и рис.4 и рис.5) можем записать выражения для коэффициентов:
 ,
,  ,
, ![]() ;
;
 ,
, ![]() ;
;  ; (32)
; (32)
![]() ,
,
![]() ;
;
![]() ,
, ![]() .
.
Здесь ![]() – значение температуры в точке
– значение температуры в точке ![]() в предыдущий момент времени,
в предыдущий момент времени, ![]() и
и![]() – значения функций
– значения функций ![]() и
и![]() в точке
в точке ![]() в текущий момент времени.
в текущий момент времени.
Запишем уравнение (24) для каждой внутренней точки. В результате, для нахождения неизвестных значений ![]() получим следующую систему линейных алгебраических уравнений с трехдиагональной матрицей
получим следующую систему линейных алгебраических уравнений с трехдиагональной матрицей
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() , (33)
, (33)
![]()
![]() ,
,
![]()
![]() .
.
Система (33) решается методом прогонки [7]. После нахождения поля температуры делается следующий шаг по времени и вычисления продолжаются до нужного момента времени.
Полученную систему линейных алгеьраических уравнений будем решать методом прогонки. Прямой ход метода прогонки состоит в вычислении прогоночных. коэффициентов ![]() и
и ![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Обратный ход метода прогонки состоит в нахождении значений неизвестных
![]() ;
; ![]() ,
, ![]() .
.
В случае, если коэффициенты системы (33) зависят от температуры ![]() , нужно организовать итерационный процесс. Значения коэффициентов следует вычислять по значениям температуры из предыдущей итерации, и решая систему (33) с постоянными коэффициентами находить новые значения температуры. Итерации продолжаются до тех пор, пока максимальная невязка системы (33) не станет меньше некоторого заданного значения.
, нужно организовать итерационный процесс. Значения коэффициентов следует вычислять по значениям температуры из предыдущей итерации, и решая систему (33) с постоянными коэффициентами находить новые значения температуры. Итерации продолжаются до тех пор, пока максимальная невязка системы (33) не станет меньше некоторого заданного значения.
Достаточным условием применимости метода прогонки является преобладание по модулю диагональных элементов матрицы системы суммы модулей соседних элементов [7]. Коэффициенты ![]() ,
, ![]() ,
, ![]() положительны, в силу постановки задачи (см. формулы (32)). Нарушение указанных достаточных условий возможно лишь при положительных значениях коэффициента
положительны, в силу постановки задачи (см. формулы (32)). Нарушение указанных достаточных условий возможно лишь при положительных значениях коэффициента ![]() (см. выражение для коэффициента
(см. выражение для коэффициента ![]() в формулах (32)). Поэтому функцию
в формулах (32)). Поэтому функцию ![]() , если это необходимо, нужно линеаризовать так, чтобы величина
, если это необходимо, нужно линеаризовать так, чтобы величина ![]() была отрицательной, либо равной нулю.
была отрицательной, либо равной нулю.
Метод КО обобщается на случай трехмерной нестационарной краевой задачи для уравнения теплопроводности.
Уравнение теплопроводности
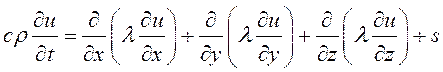 (34)
(34)
представляется в виде
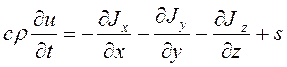 , (35)
, (35)
где 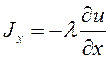 ,
, 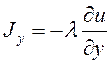 ,
,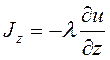 – плотности теплового потока в направлении осей
– плотности теплового потока в направлении осей ![]() ,
,![]() и
и ![]() , соответственно. Расчетная область
, соответственно. Расчетная область ![]() разбивается на множество КО. Центр каждого КО есть расчетная точка. Типичный контрольный объем
разбивается на множество КО. Центр каждого КО есть расчетная точка. Типичный контрольный объем ![]() представлен на рис.6.
представлен на рис.6.
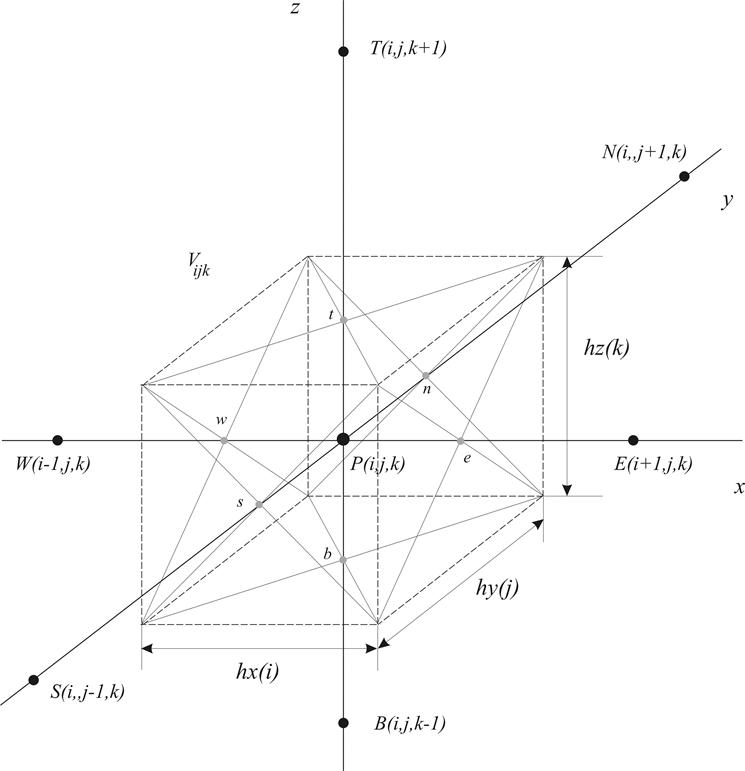
Рис.6. Типичный контрольный объем
Буквы W, Р , Е, S, N, B, T обозначают точки сетки, а именно: Р — рассматриваемая точка (Point), а W , Е, S, N, B и T – соответственно, «западная» (West) , «восточная» (East), «южная» (South), «северная» (North), «нижняя» (Bottom) и «верхняя» (Top) соседние точки. В скобках указаны индексы расчетных точек. Грани КО изображаются штриховыми линиями. Для обозначения граней КО, содержащего точку Р, используются буквы ![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() и
и ![]() . Проинтегрировав уравнение (35) по КО, получим
. Проинтегрировав уравнение (35) по КО, получим
 (36)
(36)
Здесь верхний индекс «0» обозначает известное значение температуры в начале шага по времени ![]() ,
, ![]() плотность теплового потока через грань КО, на которую указывает нижний индекс;
плотность теплового потока через грань КО, на которую указывает нижний индекс; ![]() площадь соответствующей грани, например,
площадь соответствующей грани, например, ![]() ;
; ![]() усредненный по объему источниковый член,
усредненный по объему источниковый член, ![]() объем КО.
объем КО.
Потоки тепла через грани КО ![]() и
и ![]() могут быть найдены по формулам
могут быть найдены по формулам
![]() ,
, ![]() . (37)
. (37)
Здесь ![]() проводимость между точками Р и Е, которая находится по значениям
проводимость между точками Р и Е, которая находится по значениям ![]() в этих точках. Проводимость
в этих точках. Проводимость ![]() можно вычислить по формуле (см. формулы (26) и (27))
можно вычислить по формуле (см. формулы (26) и (27))
 . (38)
. (38)
Равенства, подобные (37) и (38) , используются также для расчета соответствующих величин на других гранях. Источниковый член ![]() линеаризуется по температуре:
линеаризуется по температуре: ![]() . Если
. Если ![]() не зависит от температуры, то полагаем
не зависит от температуры, то полагаем ![]() ,
, ![]() . Подставив выражения для
. Подставив выражения для ![]() и
и ![]() в (36), получим дискретный аналог уравнения (34)
в (36), получим дискретный аналог уравнения (34)
![]() , (39)
, (39)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Уравнение вида (39) записывается для каждого КО, содержащего внутреннюю расчетную точку. С помощью граничных условий в приграничных КО выполняются преобразования, в результате которых, значения ![]() на границе не будут входить явным образом в систему уравнений. В итоге получается замкнутая система линейных алгебраических уравнений, которая может быть решена любым подходящим методом. Для решения системы в настоящей работе используется, метод переменных направлений [5, 6], основанный на методе прогонки.
на границе не будут входить явным образом в систему уравнений. В итоге получается замкнутая система линейных алгебраических уравнений, которая может быть решена любым подходящим методом. Для решения системы в настоящей работе используется, метод переменных направлений [5, 6], основанный на методе прогонки.
Суть метода переменных направлений проиллюстрируем на примере двумерной задачи. На рис. 7 изображена расчетная область в двухмерии. Через ![]() обозначен двумерный КО, другие обозначения подобны используемым на рис. 6.
обозначен двумерный КО, другие обозначения подобны используемым на рис. 6.
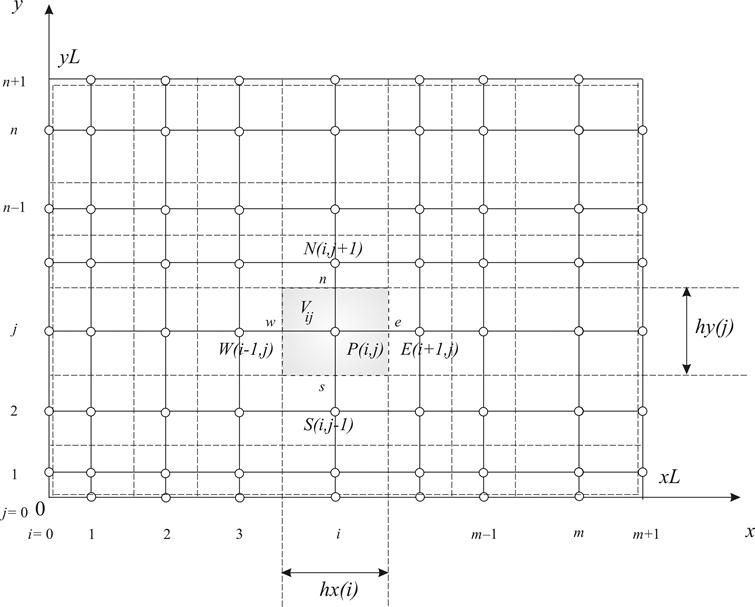
Рис. 7. Расчетная область двумерной задачи
Организуется следующий итерационный процесс. Если в дискретном аналоге нестационарного двумерного уравнения теплопроводности
![]() , (40)
, (40)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
в направлении оси ![]() предположить известными
предположить известными ![]() и
и ![]() (из предыдущей итерации), то в нем останутся только три неизвестные:
(из предыдущей итерации), то в нем останутся только три неизвестные: ![]() ,
, ![]() и
и ![]() . Построив такие уравнения с тремя неизвестными вдоль линии, параллельной оси
. Построив такие уравнения с тремя неизвестными вдоль линии, параллельной оси ![]() , получим
, получим
![]() ,
, ![]() , (41)
, (41)
где ![]() , а
, а ![]() обозначает значение
обозначает значение ![]() в соответствующей точке на предыдущей итерации. При этом, как сказано выше, с помощью граничных условий в приграничных КО выполняются преобразования, в результате которых значения
в соответствующей точке на предыдущей итерации. При этом, как сказано выше, с помощью граничных условий в приграничных КО выполняются преобразования, в результате которых значения ![]() на границе не входят в систему уравнений. В итоге получается система линейных алгебраических уравнений с трехдиагональной матрицей, которая решается методом прогонки.
на границе не входят в систему уравнений. В итоге получается система линейных алгебраических уравнений с трехдиагональной матрицей, которая решается методом прогонки.
Метод переменных направлений состоит в том, что вначале прогонка используется для всех линий, параллельных оси ![]() , а потом повторяется для всех линий, параллельных оси
, а потом повторяется для всех линий, параллельных оси ![]() . Рассчитанные новые значения
. Рассчитанные новые значения ![]() вдоль линии используются в качестве значений
вдоль линии используются в качестве значений ![]() при решении уравнений для соседней линии. Линии выбираются в произвольной последовательности. В настоящей работе сначала рассматривается линия вдоль оси
при решении уравнений для соседней линии. Линии выбираются в произвольной последовательности. В настоящей работе сначала рассматривается линия вдоль оси ![]() сразу над нижней границей
сразу над нижней границей ![]() . Затем все параллельные ей линии перебираются снизу вверх до верхней границы
. Затем все параллельные ей линии перебираются снизу вверх до верхней границы ![]() и в обратном направлении. После этого выполняется прогонка по всем линиям вдоль оси
и в обратном направлении. После этого выполняется прогонка по всем линиям вдоль оси ![]() слева направо и обратно. Такой алгоритм обеспечивает быстрое «проникновение» информации о граничных условиях во внутреннюю часть расчетной области.
слева направо и обратно. Такой алгоритм обеспечивает быстрое «проникновение» информации о граничных условиях во внутреннюю часть расчетной области.
В трехмерии добавляется направление вдоль оси ![]() .
.
4. Пример расчета
В качестве примера, был выполнен расчет динамики температурного поля грунтов основания здания рис.1 с размерами в горизонтальном сечении 20 м х 8 м. Координаты вершин здания (в метрах), соответственно, равны (0,0), (10,0), (10,4) и (0,4). Размеры области ![]() выбирались равными
выбирались равными ![]() =21 м,
=21 м, ![]() =15 м,
=15 м, ![]() =17 м. В расчетной области выделялось три литологических слоя (как на рис.1). Физические характеристики литологических слоев, необходимые для расчета, приведены в табл. 1 [3].
=17 м. В расчетной области выделялось три литологических слоя (как на рис.1). Физические характеристики литологических слоев, необходимые для расчета, приведены в табл. 1 [3].
Температура на нижней границе расчетной области ![]() (см. рис. 1) полагалась равной
(см. рис. 1) полагалась равной ![]() -1,4. На верхней границе области
-1,4. На верхней границе области ![]() выделялось 3 зоны (см. рис.2). В зоне 2 (где находится здание) физические характеристики остаются постоянными во времени. Условия в зонах 1 и 3 изменяются по интервалам времени – месяцам года (см. табл. 2). За начало отсчета принимается 01 января текущего года: момент начала эксплуатации здания. Через год эти условия повторяются, т.е. условия на верхней границе являются периодическими функциями времени с периодом
выделялось 3 зоны (см. рис.2). В зоне 2 (где находится здание) физические характеристики остаются постоянными во времени. Условия в зонах 1 и 3 изменяются по интервалам времени – месяцам года (см. табл. 2). За начало отсчета принимается 01 января текущего года: момент начала эксплуатации здания. Через год эти условия повторяются, т.е. условия на верхней границе являются периодическими функциями времени с периодом ![]() часов (1 год=8760 часов). Начальное распределение температуры по глубине представлено в табл. 3.
часов (1 год=8760 часов). Начальное распределение температуры по глубине представлено в табл. 3.
Таблица 1
Физические характеристики литологических слоев
Номер слоя | Характеристика | ||||||
rd, кг/м3 | сd, ккал/(кг·°С) | Wtot, доли | lM, ккал/(м·ч·°С) | lT, ккал/(м·ч·°С) | Ww (u), доли | ||
u,°С | WW (u) | ||||||
1 | 1390 | 0,22 | 0,25 | 1,3 | 1,15 | -0,3 | 0,14 |
-1,0 | 0,12 | ||||||
-10,0 | 0,08 | ||||||
2 | 1520 | 0,24 | 0,22 | 1,55 | 1,55 | -0,3 | 0,12 |
-1,0 | 0,08 | ||||||
-10,0 | 0,05 | ||||||
3 |
1500
| 0,23 | 0,27 | 2,35 | 2,15 | 0 | 0 |
0 | 0 | ||||||
0 | 0 | ||||||
Решение краевой задачи (2) – (6) методом контрольного объема осуществлялось с помощью программы, написанной на языке Visual Fortran. При этом область ![]() разбивалась сначала на блоки, а затем блоки дополнительно разбивались на более мелкие контрольные объемы (ячейки). Размеры блоков в метрах по направлениям осей следующие:
разбивалась сначала на блоки, а затем блоки дополнительно разбивались на более мелкие контрольные объемы (ячейки). Размеры блоков в метрах по направлениям осей следующие:
по оси ![]() : 3, 3, 2, 2, 2, 3, 3, 3;
: 3, 3, 2, 2, 2, 3, 3, 3;
по оси ![]() : 2, 2, 2, 3, 3, 3;
: 2, 2, 2, 3, 3, 3;
по оси ![]() : 2, 2, 2, 2, 3, 3, 3.
: 2, 2, 2, 2, 3, 3, 3.
Всего блоков 8x6x7=336.
Разбиение блоков на ячейки выполнялось следующим образом. В каждом блоке по всем трем направлениям ![]() ,
, ![]() и
и ![]() вводилась равномерная сетка: длины блоков по
вводилась равномерная сетка: длины блоков по ![]() ,
, ![]() и
и ![]() делились на 5 частей. Таким образом, в результате число контрольных объемов по
делились на 5 частей. Таким образом, в результате число контрольных объемов по ![]() ,
, ![]() и
и ![]() составило, соответственно, 40, 30 и 35, т.е. общее число элементов в расчетной области (это же число равняется числу внутренних расчетных точек в области
составило, соответственно, 40, 30 и 35, т.е. общее число элементов в расчетной области (это же число равняется числу внутренних расчетных точек в области ![]() ) равняется 40x30x35=42000. Минимальный безразмерный шаг по пространству
) равняется 40x30x35=42000. Минимальный безразмерный шаг по пространству ![]() = 0.4/L=0.019,
= 0.4/L=0.019, ![]() = 0.6/L=0.029; безразмерный шаг по времени
= 0.6/L=0.029; безразмерный шаг по времени ![]() =7.3/T=0.00083. Безразмерная полуширина сглаживания
=7.3/T=0.00083. Безразмерная полуширина сглаживания ![]() -функции
-функции ![]() =2.0/U=0.08.
=2.0/U=0.08.
Таблица 2
Физические характеристики на верхней границе расчетной области
Зо-ны | Характерис-тика | Месяц | |||||||||||
I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | ||
1 | Температура
| -24,6 | -23,8 | -19,2 | -9,5 | 3,7 | 13,1 | 18,0 | 12,4 | 4,6 | -4,6 | -16,4 | -22,4 |
| Термическое сопротивление R, м2·ч·°С/ккал | 2,6 | 2,7 | 2,8 | 3,0 | 1,7 | - | - | - | - | 1,3 | 2,1 | 2,3 |
| Коэффициент конвективного теплообмена | 13,8 | 12,3 | 12,3 | 12,0 | 12,1 | 12,6 | 13,4 | 13,0 | 14,3 | 13,4 | 13,5 | 12,7 |
2 | Температура
|
| |||||||||||
| Термическое сопротивление R, м2·ч·°С/ккал | R=1,8= const | |||||||||||
| Коэффициент конвективного теплообмена |
| |||||||||||
3 | Температура
| -24,6 | -23,2 | -19,2 | -9,5 | 3,7 | 13,1 | 18,0 | 12,4 | 4,6 | -4,6 | -16,4 | -22,4 |
| Термическое сопротивление R, м2·ч·°С/ккал | 4,4 | 4,4 | 4,7 | 5,0 | 2,82 | - | - | - | - | 2,14 | 3,57 | 3,59 |
| Коэффициент конвективного теплообмена | 13,8 | 12,3 | 12,3 | 12,0 | 12,1 | 12,6 | 13,4 | 13,0 | 14,3 | 13,4 | 13,5 | 12,7 |
Таблица 3
Начальное распределение температуры по глубине
Глубина, м | 1 | 3 | 5 | 7 | 9,5 | 12,5 | 15,5 |
°С | -0,1 | -0,4 | -1,0 | -1,2 | -1,4 | -1,4 | -1,4 |
5. Результаты расчетов
Ниже представлены результаты моделирования динамики температурного поля грунта в расчетной области. На вертикальных линиях, проходящих через точки наблюдения M1(1.5,1), M2(9,5) и М3(19.5,13.5) (см. рис.2), выведены на печать в определенных точках по глубине зависимости температуры ![]() в этих точках от времени
в этих точках от времени ![]() (рис.8–10). На рис.8 представлены изменения температуры за 5 лет на вертикальной прямой, проходящей через точку М1: 1 – в точке на глубине 1 м (
(рис.8–10). На рис.8 представлены изменения температуры за 5 лет на вертикальной прямой, проходящей через точку М1: 1 – в точке на глубине 1 м (![]() ); 2 – в точке на глубине 3 м (
); 2 – в точке на глубине 3 м (![]() ); 3 – в точке на глубине 5 м (
); 3 – в точке на глубине 5 м (![]() ) ; 4 – в точке на глубине 7 м (
) ; 4 – в точке на глубине 7 м (![]() ) и 5 – в точке на глубине 15.5 м (
) и 5 – в точке на глубине 15.5 м (![]() ). На рис.9–10 приведены зависимости от температуры через 5 лет. На рис.9 приведены зависимости в точках вертикальной прямой, проходящей через точку М2 (см. рис.2): 1–
). На рис.9–10 приведены зависимости от температуры через 5 лет. На рис.9 приведены зависимости в точках вертикальной прямой, проходящей через точку М2 (см. рис.2): 1– ![]() , 2 –
, 2 – ![]() , 3 –
, 3 – ![]() , 4 –
, 4 – ![]() , а на рис.10 – в точках вертикальной прямой, проходящей через точку М3 (рис.2): 1 –
, а на рис.10 – в точках вертикальной прямой, проходящей через точку М3 (рис.2): 1 – ![]() , 2 –
, 2 – ![]() , 3 –
, 3 – ![]() , 4 –
, 4 – ![]() .
.

Рис. 8. Зависимость температуры от времени в точках наблюдения (1.5,1,1), (1.5,1,3), (1.5,1,5), (1.5,1,7), (1.5,1,15.5) (кривые 1–5, соответственно)

Рис. 9. Зависимость температуры от времени в точках наблюдения (9,5,1), (9,5,3), (9,5,7), (9,5,15.5) (кривые 1–4, соответственно)
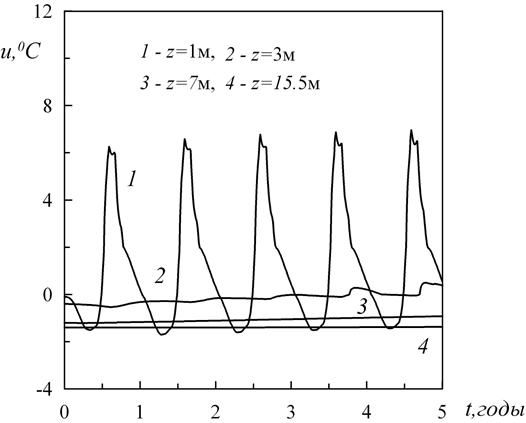
Рис. 10. Зависимость температуры от времени в точках наблюдения (19.5,13.5,1), (19.5,13.5,3), (19.5,13.5,7), (19.5,13.5,15.5) (кривые 1–4, соответственно)

Рис. 11. Распределение температуры по разрезу ![]() при
при ![]() , 3, 5, 15.5 (кривые 1–4, соответственно)
, 3, 5, 15.5 (кривые 1–4, соответственно)

Рис. 12. Распределение температуры по разрезу ![]() при
при ![]() , 3, 5, 7, 15.5 (кривые 1–5, соответственно)
, 3, 5, 7, 15.5 (кривые 1–5, соответственно)
Для исследования распределения температуры в расчетной области в фиксированный момент времени, строились соответствующие графики в разрезах, показанных на рис. 2. В качестве примера, на рис.11 представлены зависимости ![]() на указанных глубинах в разрезе
на указанных глубинах в разрезе ![]() (уравнение разреза:
(уравнение разреза: ![]() ) а на рис. 12 – зависимости
) а на рис. 12 – зависимости ![]() на разных глубинах в разрезе
на разных глубинах в разрезе ![]() (уравнение разреза:
(уравнение разреза: ![]() ). Приведенные на рис.11,12 зависимости температуры соответствуют по времени 5 годам после начала эксплуатации здания.
). Приведенные на рис.11,12 зависимости температуры соответствуют по времени 5 годам после начала эксплуатации здания.
6. Заключение.
Результаты моделирования позволяют наблюдать воздействие, оказываемое зданием на грунт, и анализировать возможность проявления опасных криогенных процессов, в результате такого воздействия.
Так например, по рис. 11 видно, что грунт под зданием через 5 лет после начала эксплуатации будет талым, в результате чего произойдет его осадка и здание окажется в аварийной ситуации. Рис. 8 демонстрирует, что на небольших глубинах, осадка произойдет существенно раньше, чем через 5 лет. Например, на глубине z=3 м (кривая 2) грунт расстаит уже в первый год эксплуатации здания.
Рис. 9–10 демонстрируют годовую периодичность процессов пучения и осадки грунта вблизи здания (точка М2) и на некотором расстоянии от него (точка М3). Периодический процесс пучения и осадки в точке М2 может привести к разрушительным последствиям.
Резкий спад температуры вдоль оси x на кривой 1 рис. 11 (обусловленный выходом за границу отапливаемого здания) указывает на возможность образования наледей.
По рис.8 видно, что в области грунта, расположенной непосредственно под зданием, по прошествии нескольких лет температура становится положительной даже на больших глубинах (примерно через 2 года − на глубине 5 м, соответствующей кривой 3, через 5 лет − на глубине 7 м, соответствующей кривой 4). Если, например, грунт незасоленный песчаный (температура начала замерзания грунта ![]() ), а кровля вечномерзлых грунтов расположена выше глубины 5 м, то возможно таяние многолетнемерзлых грунтов с образованием просадки примерно через 2 года после начала эксплуатации здания. По рис.11 видно, что распределение температуры вдоль оси x на фиксированной глубине под зданием не является постоянным (см., например, кривую 3, соответствующую глубине 5 м), что означает неравномерность просадки и перекос здания.
), а кровля вечномерзлых грунтов расположена выше глубины 5 м, то возможно таяние многолетнемерзлых грунтов с образованием просадки примерно через 2 года после начала эксплуатации здания. По рис.11 видно, что распределение температуры вдоль оси x на фиксированной глубине под зданием не является постоянным (см., например, кривую 3, соответствующую глубине 5 м), что означает неравномерность просадки и перекос здания.
Благодарности. Работа выполнена при финансовой поддержке ОАО «Газпром»
[1] Алексеев С.И. Основания и фундаменты. Часть 12. СПб. , 2007г. 113с.
[2] СНиП 2.02.04-88. Основания и фундаменты на вечномерзлых грунтах. М., 1990.
[3] РСН 67-87. Инженерные изыскания для строительства. Составление прогноза изменений температурного режима вечномерзлых грунтов численными методами. М., 1987.
[4] Самарский А.А., Вабищевич. Вычислительная теплопередача. М.: Едиториал УРСС, 2003. 784 с.
[5] Патанкар С.В. Численные методы решения задач теплообмена и динамики жидкости. М: Энергоатомиздат, 1984. 152 с. (Перевод с английского. Patankar S.V. Numerical heat transfer and fluid flow. New York: Hemisphere Publishing Corporation, 1980)
[6] Патанкар С.В. Численное решение задач теплопроводности и конвективного теплообмена при течении в каналах. М.: Издательство МЭИ, 2003. 312 с. (Перевод с английского. Patankar S.V. Computation of conduction and duct flow heat transfer. Innovative Research, Inc., 1991)
[7] Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989. 432 с.
Публикации с ключевыми словами: уравнение теплопроводности, фазовые переходы, основания фундаментов, криолитозона, криогенные процессы
Публикации со словами: уравнение теплопроводности, фазовые переходы, основания фундаментов, криолитозона, криогенные процессы
Смотри также:
- 77-30569/330390 Математическое моделирование управления нестационарным температурным полем в двухфазных средах
- Определение коэффициента теплопередачи термостабилизатора грунта в зависимости от скорости обдувающего ветра
- Алгоритмы численного анализа неклассических математических моделей термомеханики
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



