научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 03, март 2011
МГТУ им. Н. Э. Баумана
В классической механике под механическими связями принято понимать ограничения, которые накладываются на координаты и скорости механической системы. Математическим описанием таких связей служат системы равенств и неравенств, связывающие скорости, пространственные координаты элементов системы и время. В теоретических исследованиях по технологии машиностроения, где акценты смещены с динамических характеристик системы на ее статическое состояние, этому понятию дается более узкое толкование. Под механическими связями понимают совокупность соединений и сопряжений деталей, которые доставляют машине или механическому прибору геометрическую и функциональную тождественность.
Геометрическая тождественность – это пространственная взаимосвязь деталей, задаваемая конструкторской документацией и достигаемая взаимной координацией деталей. В данной работе рассматривается только это свойство механических систем. Процессы координации деталей и сборочных единиц при обработке, сборке и транспортировке исследуются в разделе технологии машиностроения, который называется теорией базирования [7].
Ограничимся обсуждением механических систем (машин, приборов, аппаратов, установок и пр.), элементы которых могут рассматриваться как твердые тела. Из теоретической механики известно, что любое свободное твердое тело в пространстве имеет шесть степеней свободы. Оно может перемещаться параллельно трех координатных осей и вращаться вокруг них. Для того чтобы зафиксировать твердое тело, на него необходимо наложить шесть геометрических связей. В технологии машиностроения эти связи называются опорными точками. Для размещения опорных точек требуется выбрать три поверхности детали или заменяющих их совокупности конструктивных элементов (пересечение поверхностей, оси или плоскости симметрии, технологическая разметка и пр.). Поверхность или иной конструктивный элемент, используемый для размещения опорных точек в процессе базирования, называется базой. В технологических исследованиях предложена развитая классификация баз [6], в данной работе будем рассматривать только базы, которые используются для координации деталей и сборочных единиц в составе изделия. Такие базы называются конструкторскими. Главной и высшей таксономией конструкторских баз является их разделение на основные и вспомогательные. Основные принадлежат элементу механической системы (детали или сборочной единице) и служат для определения его положения в составе изделия. Вспомогательные базы – это базы, предназначенные для определения положения присоединяемых элементов (деталей и сборочных единиц).
Таким образом, конструкторские базы представляют собой конструктивно реализованные координатные системы, предназначенные для ориентации и координации деталей в процессе сборки изделия. С точки зрения взаимной скоординированности составляющих элементов, изделие в целом можно рассматривать как совокупность деталей, связанных отношением базирования.
Отношение базирования влияет на важнейшие конструктивные и технологические свойства изделий. Например, от него зависят допустимые варианты декомпозиции на сборочные единицы. Это отношение определяет многие проектные решения, принимаемые на этапе разработки технологии сборки и ремонта машины или механического прибора. В многочисленных исследованиях отечественных и зарубежных авторов [8, 9] отношение базирования рассматривалось как бинарное, а для его описания использовался аппарат теории графов и математической логики. Подобная формализация оказалась недостаточной, поскольку, во многих случаях, это отношение имеет переменную местность. В данной работе предлагается новый способ описания базирования при помощи так называемых гиперсетей.
Обозначим через ![]() множество деталей изделия, а через B – отношение базирования, заданное на этом множестве. Пусть элементы
множество деталей изделия, а через B – отношение базирования, заданное на этом множестве. Пусть элементы ![]() подмножества
подмножества ![]() являются носителями вспомогательных конструкторских баз для некоторого элемента
являются носителями вспомогательных конструкторских баз для некоторого элемента ![]() . Запишем это утверждение в виде
. Запишем это утверждение в виде ![]() . Это означает, что положение собственной системы координат
. Это означает, что положение собственной системы координат ![]() задается в системе координат (СК), внешней относительно
задается в системе координат (СК), внешней относительно ![]() , и элементы этой СК принадлежат
, и элементы этой СК принадлежат ![]() . Так как положение каждой детали в пределах изделий определено, то
. Так как положение каждой детали в пределах изделий определено, то ![]() существует, возможно, не единственное подмножество
существует, возможно, не единственное подмножество ![]() такое, что
такое, что ![]() . Каждая
. Каждая ![]() связана с
связана с ![]() по крайней мере одной координатой, поэтому максимальная длина любого вектора
по крайней мере одной координатой, поэтому максимальная длина любого вектора ![]() не превосходит 7. Количество деталей в
не превосходит 7. Количество деталей в ![]() , распределение координатных связей по элементам и общее число опорных точек детали
, распределение координатных связей по элементам и общее число опорных точек детали ![]() зависят от конструкции изделия, принятых способов базирования и назначения самой детали
зависят от конструкции изделия, принятых способов базирования и назначения самой детали ![]() .
.
Все векторы вида ![]() обладают свойством перестановочности. Это значит, что если некоторый вектор
обладают свойством перестановочности. Это значит, что если некоторый вектор ![]() принадлежит B, то вектор, образованный из
принадлежит B, то вектор, образованный из ![]() перестановкой его элементов
перестановкой его элементов ![]() , также принадлежит B для любой подстановки
, также принадлежит B для любой подстановки ![]() порядка k+1, действующей на множестве
порядка k+1, действующей на множестве ![]() . Это следует из того, что элементы
. Это следует из того, что элементы ![]() образуют геометрически определенную группировку деталей, поскольку положение любой
образуют геометрически определенную группировку деталей, поскольку положение любой ![]() в системе координат, образованной деталями
в системе координат, образованной деталями ![]() , также является определенным.
, также является определенным.
Алгебраически и комбинаторные свойства объектов, для которых понятие системы координат является осмысленным, изучаются в теории матроидов. Свойство, аналогичное перестановочности векторов ![]() , постулируется в теории матроидов как присущее любым координатизуемым системам и называется аксиомой замены Штейница [1]. Из перестановочности векторов
, постулируется в теории матроидов как присущее любым координатизуемым системам и называется аксиомой замены Штейница [1]. Из перестановочности векторов ![]() следует один очень важный для технологии сборки вывод – разделение баз на основные и вспомогательные не является жестким и однозначным, оно зависит от принятой последовательности установки деталей. Поскольку порядок перечисления элементов
следует один очень важный для технологии сборки вывод – разделение баз на основные и вспомогательные не является жестким и однозначным, оно зависит от принятой последовательности установки деталей. Поскольку порядок перечисления элементов ![]() не имеет значения, то будем записывать их в нотации множеств
не имеет значения, то будем записывать их в нотации множеств ![]() и называть B-множествами.
и называть B-множествами.
Взаимная скоординированность элементов B-множеств достигается реализацией механических связей, поэтому необходимо предложить математическую модель, которая описывает соединения и сопряжения, существенные для отношения базирования. В [2] показано, что такой моделью может быть представление связей в виде гиперсети.
Гиперсетью называется вектор вида ![]() , где
, где
![]() — множество вершин;
— множество вершин;
![]() — множество ветвей;
— множество ветвей;
![]() — множество ребер;
— множество ребер;
P — отображения вида ![]() , ставящее в соответствие каждому элементу
, ставящее в соответствие каждому элементу ![]() множество его вершин
множество его вершин ![]() . Тем самым P определяет гиперграф
. Тем самым P определяет гиперграф ![]() на множестве вершин X;
на множестве вершин X;
F — отображение вида ![]() , сопоставляющее каждому элементу
, сопоставляющее каждому элементу ![]() множество
множество ![]() ветвей, причем семейство подмножеств
ветвей, причем семейство подмножеств ![]() содержит только связные части гиперграфа PS. Отображение F определяет гиперграф
содержит только связные части гиперграфа PS. Отображение F определяет гиперграф ![]() ;
;
W — отображение вида![]() , сопоставляющее каждому элементу
, сопоставляющее каждому элементу ![]() подмножество
подмножество ![]() его вершин, где
его вершин, где ![]() — множество вершин в PS, инцидентных ветвям
— множество вершин в PS, инцидентных ветвям ![]() . Тем самым отображение W определяет гиперграф
. Тем самым отображение W определяет гиперграф ![]() . Гиперграф PS называется первичной сетью гиперсети S, а гиперграф WS – ее вторичной сетью.
. Гиперграф PS называется первичной сетью гиперсети S, а гиперграф WS – ее вторичной сетью.
Изделию X сопоставим гиперсеть ![]() , в которой:
, в которой:
вершины из ![]() представляют детали;
представляют детали;
множество ветвей ![]() описывает механические связи, наложенные на детали;
описывает механические связи, наложенные на детали;
каждое ребро ![]() соответствует B-множеству деталей.
соответствует B-множеству деталей.
Отображение ![]() сопоставляет каждой ветви пару деталей, между которыми существует в изделии X механическая связь (соединение или сопряжение),
сопоставляет каждой ветви пару деталей, между которыми существует в изделии X механическая связь (соединение или сопряжение), ![]() . Таким образом, первичная сеть
. Таким образом, первичная сеть ![]() представляет собой граф механических связей. Вторичная сеть
представляет собой граф механических связей. Вторичная сеть ![]() гиперсети S связывает детали изделия таким образом, что отображение W каждому ребру
гиперсети S связывает детали изделия таким образом, что отображение W каждому ребру ![]() ставит в соответствие B-множество деталей. Поскольку в общем случае
ставит в соответствие B-множество деталей. Поскольку в общем случае ![]() , то вторичная сеть гиперсети S представляет собой гиперграф. Так как взаимная скоординированность деталей достигается наложением механических связей, то образами произвольных B-множеств являются связные подграфы первичной сети PS, т.е. условие связности элементов, составляющих семейство
, то вторичная сеть гиперсети S представляет собой гиперграф. Так как взаимная скоординированность деталей достигается наложением механических связей, то образами произвольных B-множеств являются связные подграфы первичной сети PS, т.е. условие связности элементов, составляющих семейство ![]() , выполняется.
, выполняется.

Рис. 1. Чертеж конструкции редуктора
На рис. 1 приведен чертеж конструкции редуктора, а на рис.2 изображена сопоставленная этому изделию гиперсеть. Напомним, что по правилам построения гиперсети деталям конструкции соответствуют вершины. На приведенных рисунках они обозначены одинаковыми номерами. Первичную сеть PS образуют все ребра, которые на рис.2 изображены прямыми линиями. Гиперребра вторичной сети изображены сплошными замкнутыми линиями (например, {11, 16, 21}) и жирными линиями. Таким образом, последние обозначают связи, которые входят как в первичную, так и во вторичную сети. Это дублирование необходимо, поскольку точное изображение всех связей чрезмерно усложнит рисунок и затруднит его восприятие.
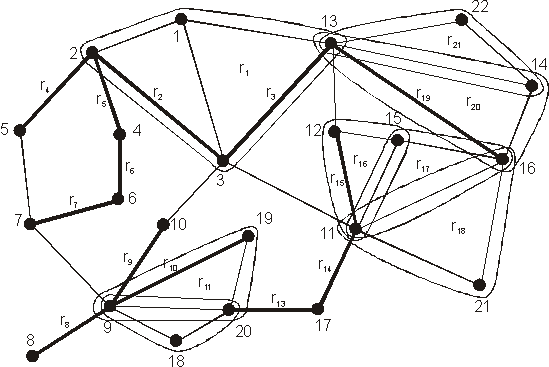
Рис. 2. Гиперсеть редуктора
Первичная сеть PS по сути дела представляет собой граф механических связей, свойства которого подробно обсуждались в многочисленных исследованиях по теории проектирования [3,7]. Эта структурная модель не дает точного описания отношения базирования B, поскольку она не способна выделить многоместные группировки детали, являющиеся B-множествами. Кроме того, некоторые механические связи не используются для достижения определенности базирования, а выполняют иные функции (устойчивость, кинематические связи и пр.). Адекватной структурной моделью отношения базирования является вторичная сеть WS.
Не рассматривая многочисленные конструктивные и технологические закономерности принятия решений при выборе схем базирования, будем считать, что такой выбор осуществлен, а его результаты зафиксированы в структуре вторичной сети WS.
Приведем несколько определений из теории гиперграфов [4], которые будут использованы для математического описания таких важных технологических категорий, как последовательность сборки и схема технологического членения (схема разузлования). В этих определениях вторичная сеть рассматривается как просто пример гиперграфа, лишенного фиксированного технологического содержания.
Определение 1:
Подграф ![]() гиперграфа
гиперграфа ![]() называется полновершинным суграфом, если
называется полновершинным суграфом, если ![]() . Иными словами,
. Иными словами, ![]() получается из WS удалением ребер, входящих
получается из WS удалением ребер, входящих ![]() . Такое удаление называется слабым. Подграф
. Такое удаление называется слабым. Подграф ![]() называется усеченным суграфом гиперграфа
называется усеченным суграфом гиперграфа ![]() , если
, если ![]() , где
, где ![]() . Удаление ребер вместе с инцидентными вершинами называется сильным.
. Удаление ребер вместе с инцидентными вершинами называется сильным.
Определение 2:
Стягиванием ребра ![]() в гиперграфе
в гиперграфе ![]() называется операция, состоящая из слабого удаления этого ребра и, в случае
называется операция, состоящая из слабого удаления этого ребра и, в случае ![]() , последующей замены всех вершин
, последующей замены всех вершин ![]() новой вершиной, инцидентной каждому ребру из
новой вершиной, инцидентной каждому ребру из ![]() , которые в WS были инцидентны, по крайней мере, одной вершине множества
, которые в WS были инцидентны, по крайней мере, одной вершине множества ![]() . Более формально: если
. Более формально: если ![]() — гиперграф, полученный из WS стягиванием ребра r, то
— гиперграф, полученный из WS стягиванием ребра r, то
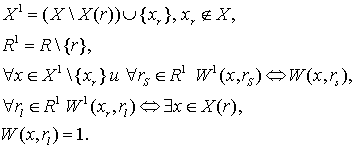
Стягивание ребра ![]() может повлечь за собой частичное или полное отождествление вершин во множествах
может повлечь за собой частичное или полное отождествление вершин во множествах ![]() для других ребер
для других ребер ![]() (но сами эти ребра не удаляются). Подобные отождествления допускаются лишь как индуцированные стягиванием ребра r, а не в качестве самостоятельных операций.
(но сами эти ребра не удаляются). Подобные отождествления допускаются лишь как индуцированные стягиванием ребра r, а не в качестве самостоятельных операций.
Определение 3:
Стягивание ребра будем называть нормальным, если степень ![]() стягиваемого ребра
стягиваемого ребра ![]() в гиперграфе
в гиперграфе ![]() равна 2.
равна 2.
Определение 4:
Все вершины исходного гиперграфа ![]() назовем s-вершинами. Кроме того, вершина
назовем s-вершинами. Кроме того, вершина ![]() , образованная отождествлением двух s-вершин, соединенных ребром кратности 2, называется s-вершиной.
, образованная отождествлением двух s-вершин, соединенных ребром кратности 2, называется s-вершиной.
В процессе сборки изделия происходит реализация механических связей, соединяющих устанавливаемую деталь (сборочную единицу) с «собранным фрагментом изделия» и доставляющих данному элементу определенность геометрического положения относительно системы координат этого фрагмента. Абстрагируясь от конкретных технологических приемов получения соединений и сопряжений, представим реализацию каждой механической связи в виде слабого удаления соответствующего ребра вторичной сети WS. Во всех дальнейших операциях установленные элементы выступают как некоторая «целостность». Это позволяет представить их в виде некоторой s-вершины сети WS, образованной отождествлением всех вершин, инцидентным стянутым гиперребрам.
Итак, процесс сборки изделия ![]() можно представить в виде последовательности стягиваний
можно представить в виде последовательности стягиваний
![]() вторичной сети
вторичной сети ![]() , причем для
, причем для ![]() должны выполняться условия:
должны выполняться условия:
1. ![]() ;
;
2. ![]() представляет собой одновершинный гиперграф, описывающий изделие в сборе;
представляет собой одновершинный гиперграф, описывающий изделие в сборе;
3. Каждое стягивание ребра является нормальным;
4. Для всех ![]() выполняется соотношение
выполняется соотношение ![]() .
.
Рассмотрим более подробно адекватность условия 3, поскольку обоснованность условий 1 и 3 является очевидной, а 4 с необходимостью следует из изложенного материала. Для установки некоторой детали ![]() необходимо, чтобы все детали из какой-либо совокупности
необходимо, чтобы все детали из какой-либо совокупности ![]() , образующей с
, образующей с ![]() B-множество, были скоординированы относительно друг друга. В этом случае они образуют внешнюю систему координат, определяющую положение
B-множество, были скоординированы относительно друг друга. В этом случае они образуют внешнюю систему координат, определяющую положение ![]() . По определению гиперсети В-множествам деталей соответствуют ребра вторичной сети WS, а скоординированность деталей из
. По определению гиперсети В-множествам деталей соответствуют ребра вторичной сети WS, а скоординированность деталей из ![]() означает, что все механические связи, наложенные на элементы из
означает, что все механические связи, наложенные на элементы из ![]() , реализованы. Иными словами, осуществлены операции слабого удаления ребер, описывающих эти связи, и отождествление вершин. Поэтому совокупности
, реализованы. Иными словами, осуществлены операции слабого удаления ребер, описывающих эти связи, и отождествление вершин. Поэтому совокупности ![]() соответствует одна вершина в некотором
соответствует одна вершина в некотором ![]() . Таким образом, ребро r, соединяющее в
. Таким образом, ребро r, соединяющее в ![]()
![]() и
и ![]() имеет степень 2, а установка
имеет степень 2, а установка ![]() на
на ![]() описывается нормальным стягиванием.
описывается нормальным стягиванием.
На рис. 3 показана вторичная сеть WS редуктора (см. рис.1), а на рис. 4 представлен фрагмент последовательности P(WS) нормальных стягиваний этой гиперсети.

Рис. 3. Вторичная сеть WS редуктора
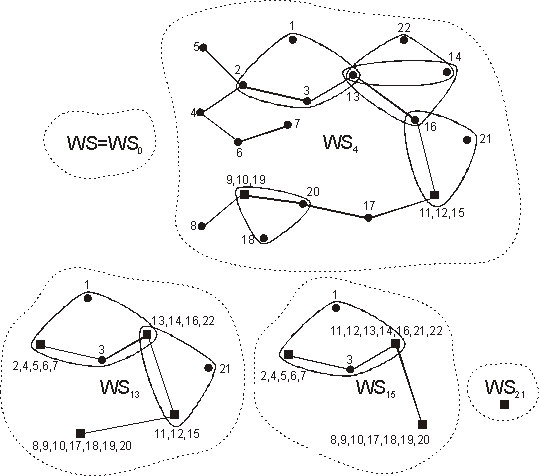
Рис. 4. Фрагмент последовательности нормальных стягиваний вторичной сети редуктора
На рис. 4 черными квадратами изображены составные вершины. Это вершины, состоящие из нескольких простых вершин, которые продуцирует процедура стягиваний вторичной сети. Так, гиперграф ![]() получается из вторичной сети
получается из вторичной сети ![]() нормальным стягиванием по ребрам {9,10}, {9,19}, {11,12} и {11,12,15}. Нормальные стягивания ребер гиперграфа
нормальным стягиванием по ребрам {9,10}, {9,19}, {11,12} и {11,12,15}. Нормальные стягивания ребер гиперграфа ![]() {2,5}, {2,4}, {4,6}, {6,7}, {8,{9,10,19}}, {{9,10,19},20}, {18,20}, {9,10,19} и {17,20} дает гиперграф
{2,5}, {2,4}, {4,6}, {6,7}, {8,{9,10,19}}, {{9,10,19},20}, {18,20}, {9,10,19} и {17,20} дает гиперграф ![]() и т.д. до реализации всех связей и генерации одновершинного гиперграфа.
и т.д. до реализации всех связей и генерации одновершинного гиперграфа.
Это первая статья цикла работ, посвященного моделированию механических связей при помощи гиперграфов. Автор надеется опубликовать продолжение исследований в следующих номерах данного электронного издания.
Список литературы
1. Айгнер М. Комбинаторная теория. – М.: Мир, 1982. – 558 с.
2. Божко А.Н. Выбор рациональной последовательности сборки изделия// Электронное научно-техническое издание «Наука и образование» – 2010. – ╧7
3. Божко А. Н., Бетин Е. А. Анализ стягиваемости гиперграфов// Информационные технологии. – 2005. – ╧5 – с. 6-12.
4. Зыков А.А. Гиперграфы// УМН. – 1974. – т. XXIX, вып. 6. – с. 89-153.
5. Исследования по прикладной теории графов/ Под ред. А.С. Алексеева. – Новосибирск: Наука, 1986. – 169с.
6. Маталин А.А. Технология машиностроения. – М.: Машиностроение, 1985. – 512 с.
7. Сборка и монтаж изделий машиностроения: справочник в 2-х томах / Под ред. В.С. Корсакова, В.К. Замятина. – М.: Машиностроение, 1983. – 480+360 с.
8. Своятыцкий Д.А. Моделирование процессов сборки в робототехнических комплексах. – Минск: Наука и техника, 1983.
9. Челищев Б.Е., Боброва И.В., Гонсалес-Сабатер А. Автоматизация проектирования технологии в машиностроении – М.: Машиностроение, 1987.
Публикации с ключевыми словами: гиперграф, гиперсеть
Публикации со словами: гиперграф, гиперсеть
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



