научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 09, сентябрь 2011
УДК 004.942
МГТУ им. Н.Э. Баумана
Еще со времен первых работ по теории систем во многих отраслях научного знания утвердилась и получила развитие так называемая структурная парадигма, когда свойства целого выводятся из характеристик элементов и связей между ними. Эта доктрина оказалась плодотворной не только в естественных науках и лингвистике. Опыт показал, что структурный подход имеет множество результативных применений в теории проектирования и технологии машиностроения [7, 8, 9].
Естественным средством для описания структур технических объектов служит аппарат теории графов, с помощью которого удалось решить несколько важных прикладных задач размерного анализа, синтеза кинематических схем, функционально-стоимостного анализа и др. Известны работы, в которых авторы предлагали различные графовые модели для проектирования сборочных процессов машин и механических приборов. Эти попытки были не вполне удачными, поскольку в процессе техногенеза элементы систем часто образуют сложные «ансамбли», которые не могут быть адекватно описаны бинарными отношениями. Многие свойства сложных технических объектов порождаются в результате взаимодействия множественных совокупностей составных частей, и на статическом уровне феномены такого рода представляются многоместными отношениями или отношениями переменной местности. Технологические процессы изготовления машин и приборов изобилуют примерами отношений такого сорта. Так, базирование и геометрические связи в процессе сборки в общем случае являются многоместными и в терминах графов принципиально не могут быть описаны без потери существенных данных.
В нескольких работах автора (см. [1, 2, 3]) предложена и обоснована гиперграфовая модель конструкции машин и механических приборов. Во многих проектных ситуациях эта структурная модель адекватно описывает совокупность позиционных механических связей, доставляющих деталям изделия определенность в процессе сборки.

Рис. 1. Промежуточный вал цилиндрического редуктора внутреннего зацепления
На рис. 1 показан пример простой конструкции, а на следующем рисунке – две ее структурные модели: граф механических связей (a) и гиперграф механических связей (b).

Рис. 2. Структурные модели редуктора
Развернутое определение, примеры применения и описание области адекватности гиперграфовой модели изделия можно найти в [1]. Поскольку данная работа является продолжением цикла статей, ограничимся самыми краткими формулировками исходных понятий, необходимыми для изложения результатов.
Поставим в соответствие изделию гиперграф механических связей ![]() , где множество вершин
, где множество вершин ![]() описывает детали машины или механического прибора, множество гиперребер
описывает детали машины или механического прибора, множество гиперребер ![]() представляет минимальные геометрически определенные группировки деталей, а
представляет минимальные геометрически определенные группировки деталей, а ![]() – инцидентор, который связывает гиперребра с входящими в него вершинами.
– инцидентор, который связывает гиперребра с входящими в него вершинами.
Гиперграф называется стягиваемым (s-гиперграфом), если существует последовательность ![]() , для элементов которой выполняются следующие требования:
, для элементов которой выполняются следующие требования:
1. ![]() ;
;
2. ![]() представляет собой одновершинный гиперграф;
представляет собой одновершинный гиперграф;
3. Для всех ![]() справедливо соотношение
справедливо соотношение ![]() ;
;
4. Каждый элемент последовательности ![]() получается из предыдущего
получается из предыдущего ![]() стягиванием ребра кратности 2,
стягиванием ребра кратности 2, ![]() . Такое стягивание называется нормальным.
. Такое стягивание называется нормальным.
В общем случае в стягиваемом гиперграфе существуют фрагменты, которые стягиваются независимо от своего окружения. Таковыми, в частности, являются все сборочные единицы и «образы», которые «пробегает» изделие в процессе общей сборки. Моделями таких фрагментов будут s-гиперграфы, которые являются подмножествами структуры, описывающей все изделие. Если определен гиперграф ![]() , задающий позиционные механические связи всего изделия, то каждый его s-подгиперграф полностью определяется набором своих вершин, как порожденный в
, задающий позиционные механические связи всего изделия, то каждый его s-подгиперграф полностью определяется набором своих вершин, как порожденный в ![]() . В этой ситуации s-подгиперграфы можно называть просто s-множествами, что существенно упрощает изложение материала.
. В этой ситуации s-подгиперграфы можно называть просто s-множествами, что существенно упрощает изложение материала.
Теорема 1. Если частично-упорядоченное множество ![]() имеет наибольший элемент (1), а всякое непустое подмножество – нижнюю грань, то
имеет наибольший элемент (1), а всякое непустое подмножество – нижнюю грань, то ![]() является полной решеткой [4].
является полной решеткой [4].
Доказательство.
Пусть A – непустое подмножество L. Верхний конус ![]() содержит единицу, т.е. множество
содержит единицу, т.е. множество ![]() – непусто. По условиям теоремы существует
– непусто. По условиям теоремы существует ![]() . Покажем теперь, что
. Покажем теперь, что ![]() . Если
. Если ![]() , то
, то ![]() для всех
для всех ![]() и, кроме того,
и, кроме того, ![]() для всех
для всех ![]() . Если же
. Если же ![]() для всех
для всех ![]() , то поскольку
, то поскольку ![]() , имеем
, имеем ![]() , чем и доказывается равенство
, чем и доказывается равенство ![]() . Если существует
. Если существует ![]() , то поскольку для каждого
, то поскольку для каждого ![]() справедливо соотношение
справедливо соотношение ![]()
![]() , имеем
, имеем ![]()
![]() . Если
. Если ![]() для всех
для всех ![]() , то
, то ![]() и, следовательно,
и, следовательно, ![]() . Таким образом,
. Таким образом, ![]() . Теорема доказана.
. Теорема доказана.
Пусть задан стягиваемый гиперграф ![]() . Обозначим через F(H) – множество всех s-подграфов гиперграфа
. Обозначим через F(H) – множество всех s-подграфов гиперграфа ![]() , пополненное пустым множеством
, пополненное пустым множеством ![]() . Упорядочим F(H) по теоретико-множественному включению
. Упорядочим F(H) по теоретико-множественному включению ![]() . Для любых двух s-подграфов
. Для любых двух s-подграфов ![]() и
и ![]() , принадлежащих F(H),
, принадлежащих F(H), ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() . Так как подграфы
. Так как подграфы ![]() – порожденные в H, то включение вершин
– порожденные в H, то включение вершин ![]() влечет за собой включение ребер
влечет за собой включение ребер ![]() .
.
В [2] доказана теорема, утверждающая, что если два s-подграфа ![]() s-гиперграфа H порождены своими множествами вершин
s-гиперграфа H порождены своими множествами вершин ![]() ,
, ![]() и имеют непустое пересечение
и имеют непустое пересечение ![]() , то подграф
, то подграф ![]() , порожденный этим пересечением, также является стягиваемым.
, порожденный этим пересечением, также является стягиваемым.
Если любым двум s-подграфам ![]() , имеющим пустое пересечение
, имеющим пустое пересечение ![]() вершин сопоставить
вершин сопоставить ![]() , то множество F(H) становится замкнутым относительно пересечения своих элементов. В этих условиях имеет место следующая теорема.
, то множество F(H) становится замкнутым относительно пересечения своих элементов. В этих условиях имеет место следующая теорема.
Теорема 2. Пусть ![]() – стягиваемый гиперграф. Частично-упорядоченное множество
– стягиваемый гиперграф. Частично-упорядоченное множество ![]() всех s-подграфов гиперграфа H, пополненное пустым множеством
всех s-подграфов гиперграфа H, пополненное пустым множеством ![]() , является полной решеткой.
, является полной решеткой.
Доказательство. Множество F(H) имеет наибольший элемент, которым служит гиперграф H. Для любых ![]()
![]() , если
, если ![]() , в противном случае –
, в противном случае – ![]() . Если
. Если ![]() – непустое подмножество F(H), то равенство
– непустое подмножество F(H), то равенство ![]() доказывает существование нижней грани для
доказывает существование нижней грани для ![]() . Все условия теоремы 1 выполнены, поэтому частично-упорядоченное множество
. Все условия теоремы 1 выполнены, поэтому частично-упорядоченное множество ![]() является полной решеткой.
является полной решеткой.
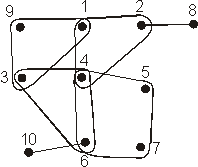
Рис. 3. Пример стягиваемого гиперграфа
На рис. 3 приведен пример стягиваемого гиперграфа H небольшой размерности, а на рис. 4 показана диаграмма Xaccе решетки ![]() всех его s-подграфов.
всех его s-подграфов.
Эта решетка не «праздно являет себя», она служит универсальной порождающей средой для генерации множества проектных решений в процессе технологической подготовки производства сборочных процессов. Приведем несколько простых интерпретаций, не требующих подробного изложения.
Любой путь в F(H) из минимального элемента (![]() ) в максимальный (H) представляет собой описание последовательности сборки, которую допускает изделие по условиям базирования. Множество всех таких путей образует исходное множество альтернатив в задаче выбора рациональной последовательности сборки в заданной технологической системе. Любая схема технологического членения изделия (т.е. разбиение конструкции на сборочные единицы) описывается деревом, вписанным в решетку F(H) и др.
) в максимальный (H) представляет собой описание последовательности сборки, которую допускает изделие по условиям базирования. Множество всех таких путей образует исходное множество альтернатив в задаче выбора рациональной последовательности сборки в заданной технологической системе. Любая схема технологического членения изделия (т.е. разбиение конструкции на сборочные единицы) описывается деревом, вписанным в решетку F(H) и др.
Исследования показали, что решетки F(H) очень богаты технологическим содержанием. Множество решеточных категорий (подрешетки, полурешетки, конгруэнции, морфизмы и др.) имеют содержательные технологические и конструктивные толкования. (Автор готовит к публикации отдельную статью, посвященную этой теме.)
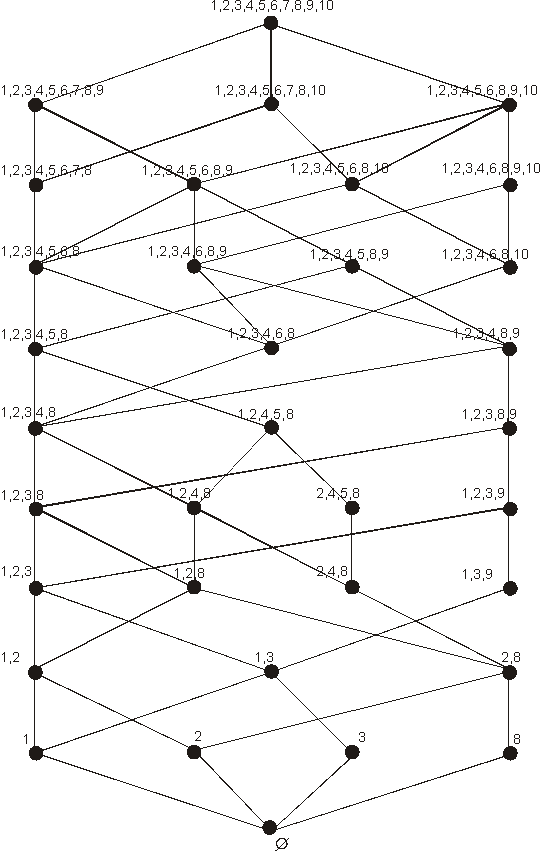
Рис. 4. Диаграмма Хассе решетки ![]()
Утверждение о решеточной организации множества всех собираемых фрагментов конструкции можно обосновать и иным способом. Обозначим через B(X) совокупность всех подмножеств множества X, включая и пустое множество. Множество B(X) иногда называют булеаном, а X – носителем. В алгебраической теории решеток доказывается теорема, гласящая, что для любого X его булеан B(X) является полной решеткой [4]. Эту решетку можно рассматривать как частично-упорядоченное множество ![]() , в котором отношение предшествования индуцируется теоретико-множественным включением
, в котором отношение предшествования индуцируется теоретико-множественным включением ![]() . Рассмотрим отображение
. Рассмотрим отображение ![]() , у которого
, у которого ![]() выполняются условия:
выполняются условия:
1. ![]() (экстенсивность);
(экстенсивность);
2. ![]() (монотонность);
(монотонность);
3. ![]() (идемпотентность).
(идемпотентность).
Отображение, обладающее свойствами 1-3, называется оператором замыкания, а элементы Y, для которых справедливо ![]() , называются замкнутыми [4].
, называются замкнутыми [4].
Теперь пусть X – множество деталей изделия, а отображение ![]() любому подмножеству
любому подмножеству ![]() ставит в соответствие
ставит в соответствие ![]() , где
, где ![]() – минимальный по составу независимо собираемый фрагмент изделия, включающий в себя Y.
– минимальный по составу независимо собираемый фрагмент изделия, включающий в себя Y.
Так как ![]() , то для отображения
, то для отображения ![]()
![]() очевидным образом выполняется свойство экстенсивности (1).
очевидным образом выполняется свойство экстенсивности (1).
Обоснуем монотонность. В самом деле, если для подмножеств деталей ![]() имеет место
имеет место ![]() , то минимальный собираемый фрагмент
, то минимальный собираемый фрагмент ![]() , включающий
, включающий ![]() , является собираемым фрагментом (возможно не минимальным), содержащим
, является собираемым фрагментом (возможно не минимальным), содержащим ![]() . Поэтому
. Поэтому ![]() .
.
Покажем идемпотентность. Для любого Y его образ ![]() является и минимальным и собираемым по определению, поэтому
является и минимальным и собираемым по определению, поэтому ![]() .
.
В такой интерпретации отображения ![]()
![]() -замкнутыми элементами в B(X) являются подмножества деталей, сборка которых может быть осуществлена независимо, и только они.
-замкнутыми элементами в B(X) являются подмножества деталей, сборка которых может быть осуществлена независимо, и только они.
Множество всех ![]() -замкнутых элементов
-замкнутых элементов ![]() называется частным по замыканию и обозначается
называется частным по замыканию и обозначается ![]() . В [4] доказывается теорема, утверждающая, что частное по замыканию
. В [4] доказывается теорема, утверждающая, что частное по замыканию ![]() оператора
оператора ![]() , действующего на решетке L, само является решеткой; причем нижние грани элементов в L совпадают с нижними гранями в
, действующего на решетке L, само является решеткой; причем нижние грани элементов в L совпадают с нижними гранями в ![]() , т.е. для любых
, т.е. для любых ![]() выполняется
выполняется ![]() .
.
Булеан B(X) множества деталей представляет собой решетку, поэтому частное ![]() по замыканию
по замыканию ![]() также является решеткой. Причем, для любых
также является решеткой. Причем, для любых ![]() , т.е. пересечение любых подмножеств, собираемых независимо, обладает этим свойством.
, т.е. пересечение любых подмножеств, собираемых независимо, обладает этим свойством.
Рассмотрим отображение ![]() , для которого выполняются требования 2 и 3 из определения оператора замыкания и, кроме того, справедливо соотношение
, для которого выполняются требования 2 и 3 из определения оператора замыкания и, кроме того, справедливо соотношение ![]() (интенсивность). Отображение с такими свойствами называется в теории решеток оператором козамыкания [4].
(интенсивность). Отображение с такими свойствами называется в теории решеток оператором козамыкания [4].
Будем считать, что интерпретация множеств ![]() осталась неизменной, а оператор козамыкания
осталась неизменной, а оператор козамыкания ![]() каждому множеству деталей Y ставит в соответствие максимальное по мощности подмножество
каждому множеству деталей Y ставит в соответствие максимальное по мощности подмножество ![]() , сборка которого может быть осуществлена независимо. Таковое всегда существует, поскольку семейство всех независимо собираемых подмножеств множества Y непусто (каждая деталь
, сборка которого может быть осуществлена независимо. Таковое всегда существует, поскольку семейство всех независимо собираемых подмножеств множества Y непусто (каждая деталь ![]() входит в это семейство). Если оператор замыкания
входит в это семейство). Если оператор замыкания ![]() добавляет детали, делающие сборку
добавляет детали, делающие сборку ![]() независимой, то оператор козамыкания удаляет «лишние» детали, нарушающие это свойство.
независимой, то оператор козамыкания удаляет «лишние» детали, нарушающие это свойство.
Подмножество ![]() , для которого
, для которого ![]() , называется козамкнутым, а совокупность всех козамкнутых элементов булеана B(X) – частным по козамыканию и обозначается
, называется козамкнутым, а совокупность всех козамкнутых элементов булеана B(X) – частным по козамыканию и обозначается ![]() . Известна теорема, гласящая, что частное по козамыканию полной решетки, также представляет собой решетку.
. Известна теорема, гласящая, что частное по козамыканию полной решетки, также представляет собой решетку.
Необходимо отметить, что в разных проектных ситуациях свойство собираемости множества деталей может получать толкования, отличающиеся от полной взаимной скоординированности по условиям базирования. Иногда любое связное подмножество деталей без обязательной взаимной координации считается собираемым. В некоторых операциях технологической подготовки производства собираемым считается группа деталей, расфасованных в специальную тару. Причем между элементами этой группы могут отсутствовать взаимная координация и механические связи [5, 6].
Для подобных случаев, когда понятие собираемости толкуется расширительно, а требования взаимной скоординированности ослабляются или снимаются, не подходит гиперграфовая формализация. Описания собираемых подмножеств при помощи операторов замыкания и козамыкания не зависят от толкования скординированности или связности подмножеств деталей, поэтому область адекватности решеток ![]() и
и ![]() больше, чем у решетки
больше, чем у решетки ![]() .
.
Список литературы
1. Божко А.Н. Моделирование механических связей изделия// Электронное научно-техническое издание «Наука и образование» – 2011. – ╧3.
2. Божко А.Н. Моделирование механических связей изделия. Условия стягиваемости// Электронное научно-техническое издание «Наука и образование» – 2011. – ╧5.
3. Божко А. Н., Бетин Е. А. Анализ стягиваемости гиперграфов// Информационные технологии. – 2005. – ╧5 – с. 6-12.
4. Гретцер Г. Общая теория решеток. –М.: Мир, 1982.
5. Маталин А.А. Технология машиностроения. – М.: Машиностроение, 1985.
6. Сборка и монтаж изделий машиностроения: справочник в 2-х томах / Под ред. В.С. Корсакова, В.К. Замятина. – М.: Машиностроение, 1983.
7. Своятыцкий Д.А. Моделирование процессов сборки в робототехнических комплексах. – Минск: Наука и техника, 1983.
8. Тимковский В.Г. Дискретная математика в мире станков и деталей. – М.:Наука, 1992.
9. Челищев Б.Е., Боброва И.В., Гонсалес-Сабатер А. Автоматизация проектирования технологии в машиностроении – М.: Машиностроение, 1987.
Публикации с ключевыми словами: сборка, гиперграф, нормальное стягивание вершин, последовательность сборки, алгебраическая структура, решетка, собираемость, оператор замыкания
Публикации со словами: сборка, гиперграф, нормальное стягивание вершин, последовательность сборки, алгебраическая структура, решетка, собираемость, оператор замыкания
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



