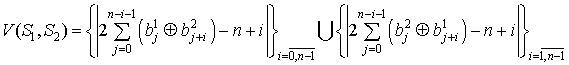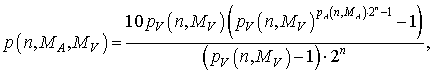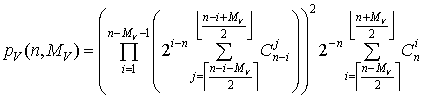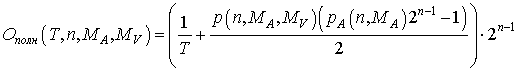научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2010
Актуальной задачей современной теории сигналов является поиск бинарных фазоманипулированных сигналов (кодов), у которых боковые лепестки автокорреляционной (АКФ) и взаимно корреляционной (ВКФ) функций имеют уровни меньшие либо равные заданным значениям (MA и MV соответственно). Такие сигналы можно представить в виде (1) [1, 2]:
| (1) |
где n > 2 – битовая длина такого сигнала, S(t) - огибающая сигнала, w0 – частота несущей, q = {0, p} – фаза.
Биты сигнала можно представить в виде бинарного множества коэффициентов ![]() , в котором
, в котором
 .
.
Множество уровней боковых лепестков АКФ задается формулой (2):
| (2) |
, где x ![]() y = x XOR y = (x + y) mod 2 - операция исключающего ИЛИ над битами x и y.
y = x XOR y = (x + y) mod 2 - операция исключающего ИЛИ над битами x и y.
Отсюда для кода, удовлетворяющего условию поиска по АКФ, необходимо выполнение неравенства (3):
| (3) |
для 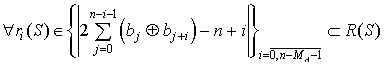 .
.
Вероятность удовлетворения произвольным кодом из диапазона ![]() условию поиска по АКФ можно оценить, используя формулу (4):
условию поиска по АКФ можно оценить, используя формулу (4):
| (4) |
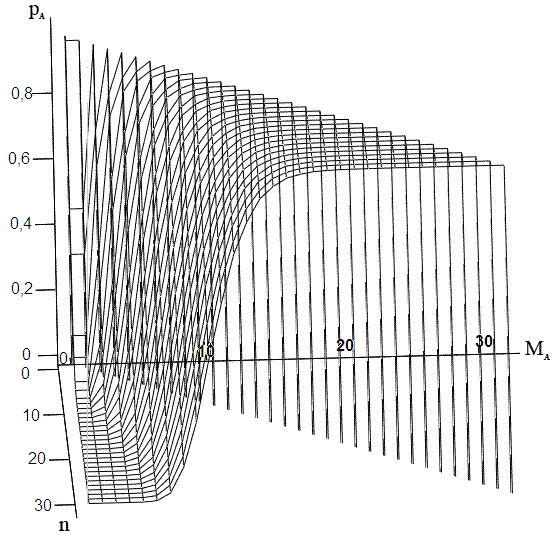
Вид зависимости (4) представлен на рис. 1.
|
Рис. 1. Зависимость оценочной вероятности нахождения кода рА по условию АКФ (вероятности возникновения состязательности) от длины кода n и максимально допустимого уровня бокового лепестка АКФ МА. |
Из соотношений (2) и (3) вытекают следующие тождества, позволяющие сократить время поиска по уровню бокового лепестка АКФ [3]:
| (5) |
где ![]() – зеркальное отображение бит последовательности S.
– зеркальное отображение бит последовательности S.
Как будет показано ниже, вероятность (4) является также вероятностью возникновения состязательности между единицами выполнения в параллельной среде.
Множество уровней лепестков ВКФ последовательностей ![]() и
и ![]() задается формулой (6):
задается формулой (6):
| (6) |
Для выполнения условия поиска по ВКФ должно выполняться неравенство (7):
| (7) |
для 
Из соотношений (5) следует, что вероятность значений всех бит кода, найденного по условию АКФ, равна 0.5. Таким образом, из формул (4) и (7) можно получить полную оценочную вероятность удовлетворения условий поиска кодов по АКФ и ВКФ – среднюю вероятность для кодов из диапазона перебора.
| (8) |
где
| (9) |
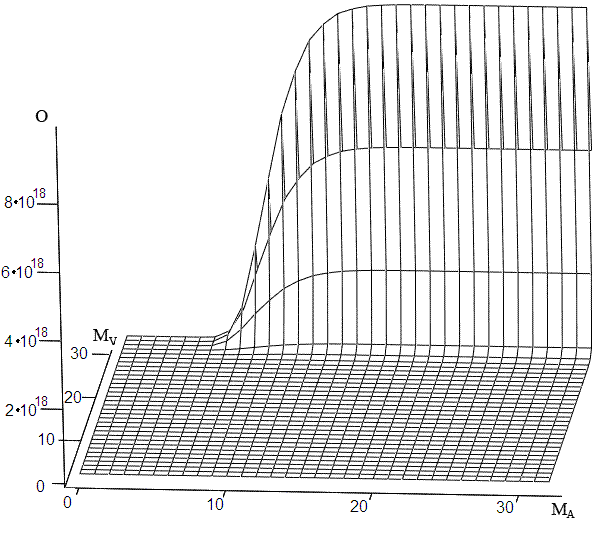
Вид функции (8) для 33-х битового кода представлен на рис. 2.
|
Рис. 2. Зависимость полной оценочной вероятности нахождения кода по условиям АКФ и ВКФ от максимально допустимых уровней АКФ и ВКФ – МА и МV. |
Архитектура параллельного пермутатора
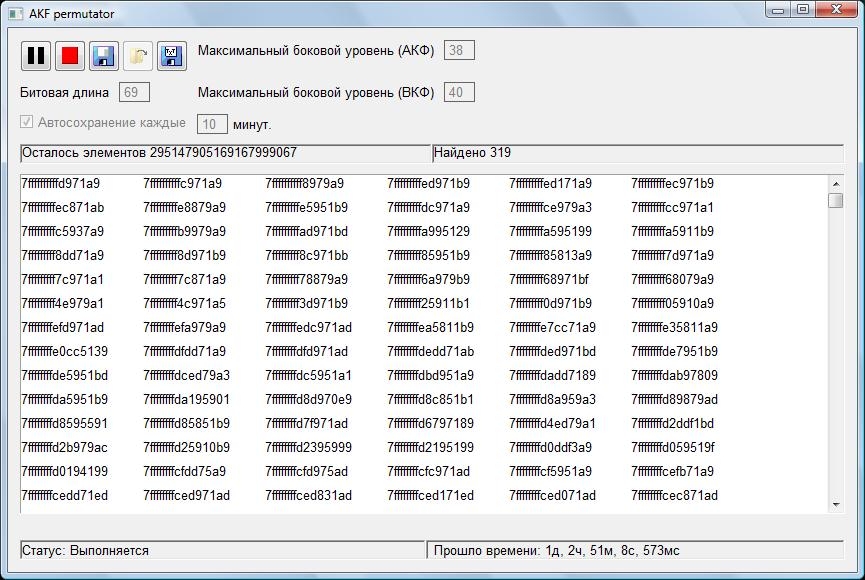
Приложение, задачей которого является перебор возможных кодов длиной от 3 до 999 бит и их анализ, разработано под операционную систему Windows и Intel-совместимые процессоры архитектуры x86, поэтому под единицами выполнения будут считаться потоки выполнения Windows.
Основными механизмами повышения скорости поиска в представленной программе (рис. 3) являются использование соотношений (5) для понижения количества итераций при переборе в ~2 раза, а также использование механизма параллельного перебора, дающего выигрыш в производительности прямо пропорциональный количеству процессоров в распространенных сегодня SMP-системах.
При запуске задачи ядро приложения (основной поток) инициализирует дескриптор вычислителя, структура которого зависит от количества процессоров, обнаруженных в системе. При обнаружении нескольких процессоров в основном потоке из отдельно создаваемой кучи выделяется собственная память потоков, инициализируемая элементами вектора, являющимися целочисленными переменными произвольной точности n, кратной 32 битам:
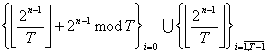 .
.
|
Рис. 3. Внешний вид разработанного пермутатора. |
Каждый поток, в качестве входного аргумента принимает дескриптор с параметрами поиска, а также свой индекс, перемножая его на  и, таким образом, получая нижнюю границу перебора. Поэтому при несоответствии проверяемого кода условию АКФ поток работает в своей области памяти, и условия состязательности не возникает. Следовательно, наиболее быстрым будет поиск со строгим условием по АКФ.
и, таким образом, получая нижнюю границу перебора. Поэтому при несоответствии проверяемого кода условию АКФ поток работает в своей области памяти, и условия состязательности не возникает. Следовательно, наиболее быстрым будет поиск со строгим условием по АКФ.
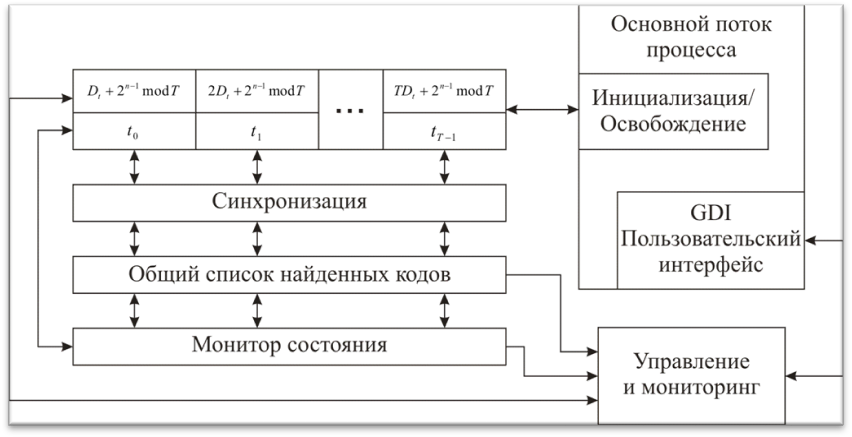
Системное управление потоками осуществляет первый созданный поток, который создается и завершается в последнюю очередь. По его состоянию определяется статус вычислителя. Грубая архитектура приложения представлена на рис. 4.
|
Рис. 4. Архитектура пермутатора. |
При поиске произвольный код из диапазона [0, 2n) с вероятностью pA удовлетворяет критерию поиска по максимально допустимой АКФ. В этом случае поток, владеющий кодом, начинает последовательный перебор кодов из списка найденных кодов.
Проверка соответствия кода условиям по АКФ (3) и ВКФ (7) производится посредством двух функций, реализующих проверку уровней боковых лепестков функции (со сдвигом – ConvolutionSh) и основного лепестка функции (без сдвига – ConvolutionNsh).
|
Рис. 5. Алгоритм проверки боковых лепестков корреляционной функции сигналов. |
Функция ConvolutionNsh проверки основного лепестка корреляционной функции заключается в простом поразрадном сложении битов сигналов по модулю 2 (операция исключающего ИЛИ) и подсчете бит результата.
Тогда проверка по формуле (3) соответствует одному вызову ConvolutionSh для lpSignal1 = lpSignal2. Проверка (7) является последовательным вызовом ConvolutionSh(lpSignal1, lpSignal2, …), ConvolutionSh(lpSignal2, lpSignal1) и ConvolutionNsh(lpSignal1, lpSignal2).
Список найденных кодов является разделяемой памятью, размером 1Мб, а также файлом, создаваемый при переполнении области списка, находящейся в ОЗУ. Разделяемый доступ требует использования механизмов синхронизации, которые, в свою очередь, создают условия возникновения состязательности между потоками. При этом, как видно из рис. 2, вероятность того, что произвольный код будет удовлетворять условиям АКФ и ВКФ с набором сигналов из общей памяти, при разумном выборе параметров поиска, будет минимальной. Поэтому для синхронизации рабочих потоков используется механизм, основанный на использовании критических участков кода со значением спин-счетчика, равным 4000 [4], а также на модели переменных условий (на вручную сбрасываемом событии). Функции, представленные здесь на языке C с использованием функционала Win32 SDK, реализуют вхождение в критические участки кода, различаемые по требуемому доступу к разделяемым ресурсам:
/*PCOMPDESCRIPTOR – тип указателя на структуру, которая описывает текущее состояние вычислителя.*/
/*Среди своих полей содержит:*/
/*CRITICAL_SECTION cs – критический участок кода со спин счетчиком, равным 4000.*/
/*HANDLE hEvent – автоматически сбрасываемое неименованное событие, создаваемое в несигнальном состоянии.*/
/*volatile DWORD dwThreadCounter – счетчик потоков, вошедших в критический участок кода для чтения (функцией LockRead).*/
/*volatile BOOL bSerialization – флаг сериализации – по умолчанию включен для SMP-систем, отключен для однопроцессорных систем.*/
/*LockWrite – вхождение в критический участок кода для записи.*/
BOOL LockWrite(PCOMPDESCRIPTOR lpComp)
{
if (lpComp->bSerialization)
{
EnterCriticalSection(&lpComp->cs);
if (lpComp->dwThreadCounter && WaitForSingleObject(lpComp->hEvent, INFINITE) == -1)
{
LeaveCriticalSection(&lpComp->cs);
return FALSE;
}else if (!lpComp->bSerialization)
/*Выход из критического участка кода, если во время ожидания была отключена сериализация*/
LeaveCriticalSection(&lpComp->cs);
}
return TRUE;
}
/* LockRead – вхождение в критический участок кода для чтения разделяемых ресурсов.*/
BOOL LockRead(PCOMPDESCRIPTOR lpComp)
{
if (lpComp->bSerialization)
{
EnterCriticalSection(&lpComp->cs);
lpComp->dwThreadCounter++;
LeaveCriticalSection(&lpComp->cs);
}
return TRUE;
}
/* UnlockWrite – выход из критического участка кода на запись.*/
VOID UnlockWrite(PCOMPDESCRIPTOR lpComp)
{
if (lpComp->bSerialization)
LeaveCriticalSection(&lpComp->lpCS);
}
/* UnlockRead – выход из критического участка кода на чтение.*/
BOOL UnlockRead(PCOMPDESCRIPTOR lpComp)
{
return !lpComp->bSerialization || (BOOL) InterlockedDecrement((volatile LONG*) &lpComp- >dwThreadCounter) || SetEvent(lpComp->hEvent);
}
В зависимости от режима работы пермутатора – однопоточном или многопоточном – необходимость в приведенном функционале может исчезать, Для включения либо отключения сериализации доступа к разделяемым ресурсам введена функция SetSerialization, вызов которой безопасен в том случае, если имеются потоки, владеющие критическим участком кода на чтение/запись:
BOOL SetSerialization(PCOMPDESCRIPTOR lpComp, BOOL bSerialize)
{
if (!bSerialize)
{
if (!lpComp->bSerialize)
return TRUE;
EnterCriticalSection(&lpComp->cs);
if (lpComp->dwThreadCounter && WaitForSingleObject(hEvent, INFINITE) == WAIT_FAILED)
{
LeaveCriticalSection(&lpComp->cs);
return FALSE;
}
lpComp->bSerialization = TRUE;
LeaveCriticalSection(&lpComp->cs);
return TRUE;
}else if (lpComp->bSerialization)
return TRUE;
else
{
if (!ResetEvent(lpComp->hEvent))
return FALSE;
lpComp->dwThreadCounter = 0;
return TRUE;
}
}
Исходя и схемы работы вычислителя, а также из (4) и (8) можно оценить сложность представленного алгоритма [5] с учетом параллельной обработки данных (10).
| (10) |
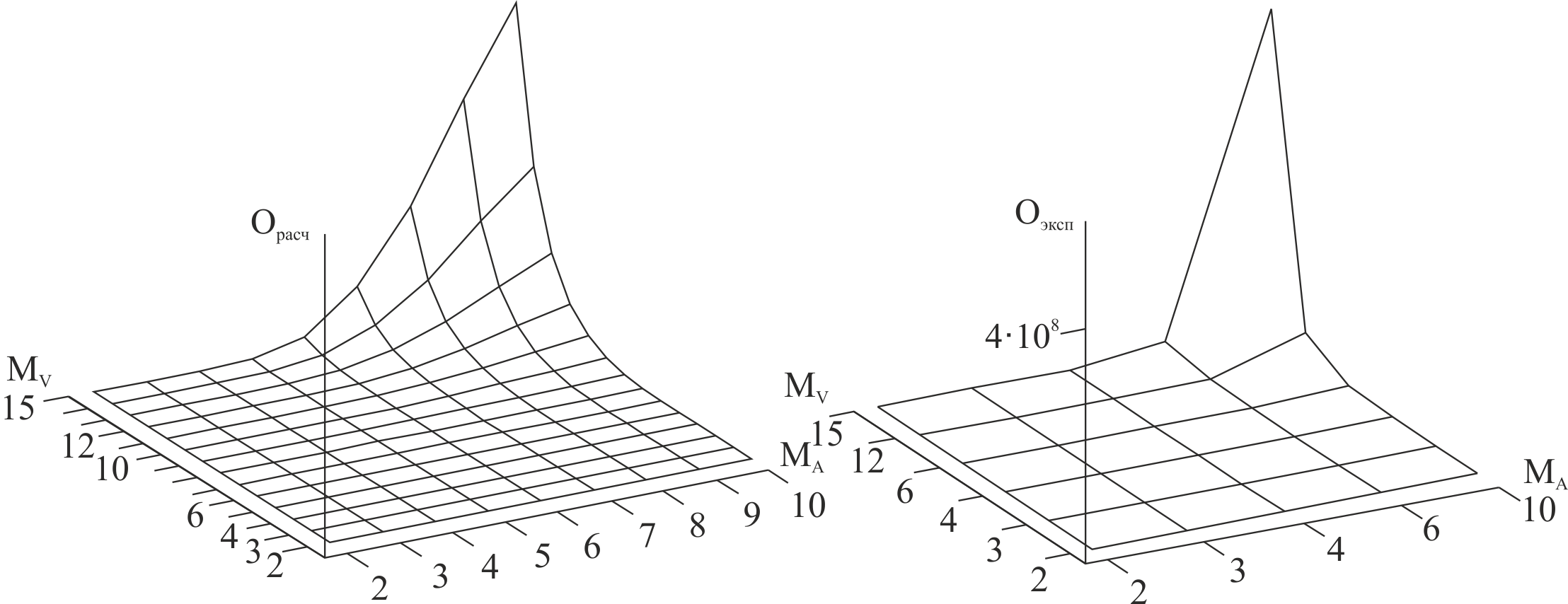
На рис. 6 приведен графический вид зависимости (10) для 33 битовых кодов. На рис. 7 слева приведена та же расчетная зависимость для MA и MV таких, что 2 ≤ MA ≤ 10, 2 ≤ MV ≤ 15. На рис. 7 справа показано время, выраженное в миллисекундах, потраченное представленным пермутатором для поиска всех 33 битовых кодов с АКФ и ВКФ с уровнями боковых лепестков меньших либо равных MA и MV таких, что ![]() на двухпроцессорной машине. Рис. 6 показывает соответствие полученного времени поиска кодов с расчетной сложностью алгоритма. Формула (10) также показывает выигрыш при использовании параллельных единиц выполнения, выраженный гиперболическим законом.
на двухпроцессорной машине. Рис. 6 показывает соответствие полученного времени поиска кодов с расчетной сложностью алгоритма. Формула (10) также показывает выигрыш при использовании параллельных единиц выполнения, выраженный гиперболическим законом.
|
Рис. 6. Расчетная сложность поиска 33 битовых сигналов на 8- процессорной ЭВМ с уровнем боковых лепестков АКФ и ВКФ меньшими либо равными MA и MV соответственно. |
|
Рис.7. Вид зависимостей, полученных теоретически (слева) и экспериментально (справа, в миллисекундах) сложности поиска 33-битовых кодов от максимально допустимых уровней MA и MV. |
Для 33 битового кода, максимальных уровней боковых лепестков АКФ 10 и ВКФ 6 получена зависимость времени вычисления в миллисекундах от количества используемых процессоров (рис. 8).
Рис. 8. Зависимость времени выполнения задачи от количества задействованных потоков для MA = 10, MV = 6. |
Заключение
Представленные эмпирические данные показывают хорошее соответствие с ожидаемыми значениями, полученными из представленных выражений, а также эффективность многопоточного синтеза при корректном использовании механизма параллельных вычислений. Хотя представленный продукт жестко привязан к архитектуре Wintel x86 (ядро реализовано на ассемблере для процессоров Intel), он, в принципе, является переносимым на другие платформы имеющие набор инструкций, близкий к семейству Intel P6, а также поддерживающие истинную многозадачность.
Список литературы
1. Шумоподобные сигналы. Анализ, синтез, обработка / В.Е. Грантмахер, Н.Е. Быстров, Д.В. Чеботарев. – СПб.: Наука и Техника, 2005. 400 с.
2. Свердлик М.Б. Оптимальные дискретные сигналы. М.: Советское радио, 1975. 200 с.
3. Чусов А. А. Поиск базиса кодов с наилучшими автокорреляционными свойствами /., Ковылин А. А.,. Родионов А.Ю., Злобин Д. В., Железняков Е. И. //Труды конференции «Вологдинские чтения», Владивосток: Издательство ДВГТУ, 2009 С. 70 - 71.
4. Харт Д. М. Системное программирование в среде Windows: пер. с англ. М.:: Вильямс, 2005. 792 с.
5. Кнут Д. Искусство программирования: в 3 т. Т. 1: Основные алгоритмы: пер. с англ. 3-е изд. перераб. и доп. М.: Вильямс, 2006. 720 с.
Публикации с ключевыми словами: многопотоковые вычисления, корреляционная функция
Публикации со словами: многопотоковые вычисления, корреляционная функция
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||
 ,
,