научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2010
МГТУ им. Н. Э. Баумана,
Постановка задачи
Требования к точности авиационных бесплатформенных инерциальных навигационных систем (ИНС) и высокий уровень погрешностей доступных на рынке чувствительных элементов – гироскопов и акселерометров – принуждают к разработке особых алгоритмов построения навигационного решения [1]. Эти алгоритмы часто содержат большое количество численных параметров, оптимальные значения которых существенным образом зависят от динамики носителя, на борту которого предполагается эксплуатация навигационной системы. Таким образом, отладка алгоритмов, повышение их надёжности и точности оказываются возможны лишь после изучения и обработки обширного массива показаний чувствительных элементов, полученных при их лётных испытаниях.
Высокая сложность и стоимость таких испытаний привели к идее имитационного моделирования сигналов инерциальных датчиков и приёмников спутниковых навигационных систем (СНС). В настоящее время на рынке представлено несколько продуктов для решения этой задачи: программные модули INS Toolbox и GPS Toolbox, разработанные фирмой GPSoft и предназначенные для подключения к математическому пакету Matlab [2]; программно-аппаратный комплекс CAST-3000/4000, предлагаемый компанией CAST Navigation [3]; виртуальная лаборатория NavLab Норвежского оборонного научно-исследовательского центра (FFI) [4]. Аналогичные инструменты имитационного моделирования обсуждаются и в публикациях [5, 6]. Все перечисленные системы имеют в своей структуре много общего. Они, как правило, включают средства генерации траектории летательного аппарата (с учётом его массогабаритных и аэродинамических характеристик) и соответствующих этой траектории идеализированных показаний гироскопов и акселерометров ИНС и приёмника СНС. Кроме того, системы моделирования содержат отдельный блок имитации погрешностей датчиков и их наложения на идеальные значения измеряемых величин.
Состоятельность такого моделирования и, следовательно, его польза для отладки навигационных алгоритмов всецело определяются точностью статистического описания ошибок чувствительных элементов навигационной системы. Погрешности гироскопов и акселерометров часто представляются как сумма постоянного смещения нуля, цветного шума с экспоненциально затухающей корреляционной функцией и белого шума. Учитываются также перекосы установки и неортогональности осей чувствительности, а для механических гироскопов, кроме того, дрейф от небаланса и неравножёсткости конструкции [3].
Такая модель погрешностей датчиков, несмотря на широкую распространённость, имеет свои изъяны. Во-первых, она предлагает единый способ описания ошибок гироскопов и акселерометров. Однако на нынешнем технологическом уровне вклад смещений нуля гироскопов в неточность выходной информации ИНС оказывается существенно выше, нежели смещений нуля акселерометров или неортогональности осей. Поэтому в некоторых аспектах модель погрешностей оказывается избыточной, в других, напротив, – недостаточной. В частности, она не позволяет описать медленное изменение смещения нуля гироскопов из-за нагрева конструкции и дрейфа параметров аналоговых электронных схем.
Во-вторых, рассмотренные системы имитационного моделирования предполагают ручной ввод всех параметров моделей ошибок датчиков. Ключевой вопрос об их идентификации в эксперименте остаётся открытым. Эта проблема приобретает особое значение, поскольку величины погрешностей чувствительных элементов в условиях движения носителя могут отличаться от тех же величин, измеренных в покое или указанных производителем в спецификации, что может быть связано с особым температурным режимом эксплуатации, вибрацией основания и т.п.
Предлагаемая в данной статье концепция полунатурного моделирования ИНС имеет своей целью построение замкнутого программного комплекса имитации показаний датчиков навигационной системы, свободного от названных недостатков. Она включает:
– имитацию пространственной траектории летательного аппарата, а также идеализированных сигналов гироскопов, акселерометров и приёмника СНС на этой траектории;
– выбор модели погрешностей чувствительных элементов, необходимой и достаточной для адекватного представления характеристик бесплатформенного инерциального измерительного блока низкого или среднего класса точности;
– проведение натурных испытаний ИНС в режиме коррекции от СНС на автомобиле;
– автоматизированное выявление статистических параметров погрешностей датчиков ИНС и СНС в соответствии с выбранной моделью по результатам натурных испытаний;
– генерацию сигналов ошибок датчиков как случайных процессов с полученными ранее статистическими параметрами и их наложение на идеальные показания.
Ценность такой методики, сочетающей численную имитацию траектории летательного аппарата с натурным экспериментом по определению погрешностей чувствительных элементов ИНС, состоит в создании без помощи специальных стендов тех условий движения и вибрации носителя, которые близки к условиям эксплуатации авиационных ИНС. Наиболее существенным отличием, влияющим на поведение погрешностей гироскопов и акселерометров, оказывается отличие спектров вибрации автомобиля и летательного аппарата. Тем не менее, если спектры не включают резонансные частоты датчиков, то и этим различием на практике можно пренебречь.
Построение траектории летательного аппарата
За основу средств имитации траектории выбрана модель динамики лёгкого самолёта с поршневым двигателем, рассматриваемого как твёрдое тело с шестью степенями свободы, движущееся над плоской невращающейся Землёй [7]. Главный вектор и главный момент сил, приложенные в центре масс самолёта, образуются активной силой ![]() и реакцией опор шасси
и реакцией опор шасси ![]() . Активная сила представляется как сумма подъёмной силы
. Активная сила представляется как сумма подъёмной силы ![]() , силы лобового сопротивления
, силы лобового сопротивления ![]() , боковой силы
, боковой силы ![]() , тяги двигателя
, тяги двигателя ![]() и силы тяжести
и силы тяжести ![]() ; момент активной силы – как сумма аэродинамических моментов крена
; момент активной силы – как сумма аэродинамических моментов крена ![]() , тангажа
, тангажа ![]() и рыскания
и рыскания ![]() :
:
![]()
Соответствующие аэродинамические коэффициенты выражаются через угол атаки ![]() , угол скольжения
, угол скольжения ![]() , углы отклонения элеронов
, углы отклонения элеронов ![]() , руля высоты
, руля высоты ![]() и руля направления
и руля направления ![]() по формулам:
по формулам:
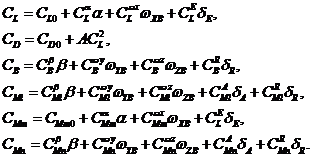
Здесь ![]() ,
, ![]() ,
, ![]() – угловые скорости самолёта относительно осей связанного трёхгранника
– угловые скорости самолёта относительно осей связанного трёхгранника ![]() , направленных соответственно к правому крылу, вперёд по продольной оси и вверх;
, направленных соответственно к правому крылу, вперёд по продольной оси и вверх; ![]() – параметр поляры. Все величины
– параметр поляры. Все величины ![]() и частные производные
и частные производные ![]() считаются постоянными.
считаются постоянными.
В аэродинамической модели учитываются ветровые возмущения. Вектор скорости самолёта относительно Земли ![]() отличается от его истинной воздушной скорости
отличается от его истинной воздушной скорости ![]() на вектор скорости ветра
на вектор скорости ветра ![]() , который задаётся как трёхмерный случайный процесс с заданной корреляционной функцией. Таким образом,
, который задаётся как трёхмерный случайный процесс с заданной корреляционной функцией. Таким образом,
![]() .
.
В расчёте углов атаки и скольжения принимает участие вектор ![]() .
.
Управление моделируемым движением самолёта осуществляется оператором при помощи джойстика либо автопилотом. Законы управления автопилота имеют вид:

где ![]() ,
, ![]() – углы крена и тангажа,
– углы крена и тангажа, ![]() ,
, ![]() – высота и её заданное значение,
– высота и её заданное значение, ![]() ,
, ![]() – приборная скорость и её заданное значение,
– приборная скорость и её заданное значение, ![]() – отклонение ручки управления двигателем. Передаточные числа
– отклонение ручки управления двигателем. Передаточные числа ![]() принимаются постоянными.
принимаются постоянными.
Координаты и скорости центра масс самолёта определяются в географическом трёхграннике ![]() , оси которого
, оси которого ![]() направлены соответственно на восток, на север и вверх по местной вертикали.
направлены соответственно на восток, на север и вверх по местной вертикали.
Угловые скорости самолёта рассчитываются на основе динамических уравнений Эйлера, углы ориентации – на основе уравнения Пуассона для матрицы перехода ![]() от связанного к географическому трёхграннику [1]:
от связанного к географическому трёхграннику [1]:
![]() ,
,
где
 .
.
Во избежание накопления вычислительных ошибок на каждом этапе расчёта выполняется ортогонализация матрицы ![]() .
.
В силу принятых допущений при расчёте траектории самолёта не делается различий между его абсолютными линейными и угловыми скоростями и теми, которые измеряются относительно географического трёхгранника. Тем не менее, на этапе формирования показаний гироскопов и акселерометров бортовой ИНС такое различение необходимо. Поэтому в рассмотрение вводятся матрицы абсолютной угловой скорости самолёта ![]() и абсолютной угловой скорости географического трёхгранника
и абсолютной угловой скорости географического трёхгранника ![]() . В этих терминах уравнение Пуассона приобретает вид [1]
. В этих терминах уравнение Пуассона приобретает вид [1]
![]() .
.
Сравнивая два выражения для ![]() , получим:
, получим:

Элементы матрицы ![]() , найденные из последнего соотношения, служат идеальными значениями показаний гироскопов ИНС.
, найденные из последнего соотношения, служат идеальными значениями показаний гироскопов ИНС.
Идеальные показания акселерометров (кажущиеся ускорения) рассчитываются как ускорения самолёта в географическом трёхграннике после вычитания вектора ускорения силы тяжести и введения кориолисовых поправок:

Здесь ![]() – относительные линейные скорости самолёта,
– относительные линейные скорости самолёта, ![]() – абсолютные угловые скорости географического трёхгранника,
– абсолютные угловые скорости географического трёхгранника, ![]() – угловая скорость Земли,
– угловая скорость Земли, ![]() – широта места. Поскольку акселерометры, как и гироскопы, установлены в бесплатформенной ИНС по осям связанного трёхгранника, то найденные значения кажущихся ускорений необходимо преобразовать к этим осям:
– широта места. Поскольку акселерометры, как и гироскопы, установлены в бесплатформенной ИНС по осям связанного трёхгранника, то найденные значения кажущихся ускорений необходимо преобразовать к этим осям:
 .
.
Программное обеспечение, реализующее модель динамики самолёта, написано для операционной системы Microsoft Windows с использованием библиотеки трёхмерной графики OpenGL. Графический интерфейс программы представлен на рис. 1.
|
Рис. 1. Графический интерфейс программы построения траектории летательного аппарата |
Моделирование погрешностей датчиков навигационной системы
Сигналы ошибок гироскопов и акселерометров ИНС, а также приёмника СНС представляются в виде случайных процессов с заданными статистическими характеристиками. Эти характеристики определяются по результатам натурных испытаний навигационной системы на автомобиле согласно особой методике оценивания погрешностей, изложенной в работах [8, 9]. В основе методики лежит тот факт, что сигналы обратной связи, вводимые в алгоритм ИНС при коррекции её показаний от СНС, содержат в себе информацию о собственных погрешностях чувствительных элементов ИНС. Таким образом, оценивание осуществляется компенсационным способом без привлечения процедур калмановской фильтрации, что повышает надёжность метода, уменьшает длительность переходных процессов и упрощает задачу автоматизации оценивания.
Погрешности гироскопов могут по выбору пользователя моделироваться одним из двух возможных способов. Первый способ предполагает так называемое волновое описание случайного процесса, при котором возмущения величины задаются последовательностью ![]() -функций Дирака [10]. Ошибка
-функций Дирака [10]. Ошибка ![]() в показаниях гироскопа образуется суммой кусочно-постоянного смещения нуля
в показаниях гироскопа образуется суммой кусочно-постоянного смещения нуля ![]() и белого шума
и белого шума ![]() :
:
![]() .
.
Возмущения сигнала ![]() задаются в виде
задаются в виде
![]() .
.
Импульсы ![]() -функций возникают в производной
-функций возникают в производной ![]() через равные интервалы времени
через равные интервалы времени ![]() , порождая ступенчатое изменение величины
, порождая ступенчатое изменение величины ![]() , а коэффициенты
, а коэффициенты ![]() определяют интенсивность каждого импульса.
определяют интенсивность каждого импульса.
Таким образом, статистическими характеристиками собственных погрешностей гироскопа являются: среднеквадратичное смещение нуля между запусками, за которое принимается начальное значение ![]() ; интервал
; интервал ![]() ; среднее значение интенсивности импульсов
; среднее значение интенсивности импульсов ![]() ; среднеквадратическое отклонение интенсивности импульсов
; среднеквадратическое отклонение интенсивности импульсов ![]() ; корень из спектральной плотности мощности белого шума
; корень из спектральной плотности мощности белого шума ![]() , где
, где ![]() – шаг дискретизации процесса моделирования по времени. Ненулевое значение
– шаг дискретизации процесса моделирования по времени. Ненулевое значение ![]() соответствует медленному изменению смещения нуля гироскопа (например, вследствие изменения температуры), а
соответствует медленному изменению смещения нуля гироскопа (например, вследствие изменения температуры), а ![]() – случайным его вариациям.
– случайным его вариациям.
На рис. 2 представлен пример оценок смещений нуля гироскопов горизонтальных каналов, полученных в рамках волновой модели при натурных испытаниях инерциального измерительного блока среднего класса точности Honeywell HG1700 [11].
|
Рис. 2. Оценки смещений нуля гироскопов, представленные волновой моделью |
Альтернативой волновой модели является более привычная непрерывная модель, согласно которой смещение нуля гироскопа образуется как сумма постоянной величины ![]() , линейного слагаемого
, линейного слагаемого ![]() и коррелированного шума
и коррелированного шума ![]() :
:
![]() .
.
Параметры ![]() и
и ![]() отыскиваются при обработке результатов испытаний методом наименьших квадратов и затем служат в качестве среднеквадратических отклонений при моделировании случайного линейного тренда в смещении нуля гироскопа. Для остаточного сигнала
отыскиваются при обработке результатов испытаний методом наименьших квадратов и затем служат в качестве среднеквадратических отклонений при моделировании случайного линейного тренда в смещении нуля гироскопа. Для остаточного сигнала ![]() задаётся экспоненциально затухающая корреляционная функция
задаётся экспоненциально затухающая корреляционная функция
![]() ,
,
где ![]() . Расчёт интервала корреляции
. Расчёт интервала корреляции ![]() осуществляется по формуле
осуществляется по формуле
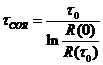 ,
,
величина ![]() предварительно выбирается такой, чтобы выполнялось условие
предварительно выбирается такой, чтобы выполнялось условие ![]() . Вычислительная сложность алгоритма составляет
. Вычислительная сложность алгоритма составляет ![]() , где
, где ![]() – длина массива данных
– длина массива данных ![]() ,
, ![]() .
.
На рис. 3 приведены оценки тех же смещений нуля гироскопов, что и на рис. 2, но представленные непрерывной моделью. Тонкой линией отмечен линейный тренд ![]() .
.
|
Рис. 3. Оценки смещений нуля гироскопов, представленные непрерывной моделью |
Смещения нуля акселерометров, как показано в работе [8], наблюдаемы лишь при поворотах автомобиля, на котором установлена испытываемая ИНС. Таким образом, для них практически невозможно выявление нестабильности в течение одного запуска. Поэтому модель погрешностей акселерометров ![]() включает только постоянное смещение нуля
включает только постоянное смещение нуля ![]() и белый шум
и белый шум ![]() :
:
![]() .
.
Такое упрощение модели допустимо, поскольку вклад погрешностей измерения ускорений в выходную ошибку ИНС по скорости существенно меньше, нежели погрешностей определения угловой скорости. Действительно, если принять типичные для инерциального измерительного блока Honeywell HG1700 значения ![]() ° / ч,
° / ч, ![]() м / с2, то из анализа решений уравнений ошибок ИНС [1] можем получить приближённые величины вклада каждой из погрешностей в амплитуду ошибки по скорости:
м / с2, то из анализа решений уравнений ошибок ИНС [1] можем получить приближённые величины вклада каждой из погрешностей в амплитуду ошибки по скорости:
![]() м / с,
м / с, ![]() м / с.
м / с.
Здесь ![]() – радиус Земли.
– радиус Земли.
Статистическими характеристиками погрешностей СНС по скорости служат задержка показаний ![]() , принимаемая детерминированной константой, и интенсивность аддитивного белого шума
, принимаемая детерминированной константой, и интенсивность аддитивного белого шума ![]() :
:
![]() .
.
Методика оценивания этих величин на основе измерения рассогласований ИНС и СНС по скорости рассмотрена в работе [9].
Погрешности датчиков, сымитированные с учётом найденных характеристик, накладываются на их идеальные показания, и могут служить тестовым материалом для отладки навигационных алгоритмов автономных и корректируемых бесплатформенных навигационных систем. На рис. 4 представлен пример вычисления скорости традиционным алгоритмом ИНС [1] по имитируемым показаниям гироскопов и акселерометров блока Honeywell HG1700 на модельной траектории полёта самолёта Cessna 172P. На участках взлёта, разворотов и посадки управление осуществлялось вручную, на прямолинейных отрезках – при помощи автопилота.
|
Рис. 4. Показания по скорости ИНС (толстая линия) и СНС (тонкая линия), полученные по имитируемым показаниям датчиков |
Используемая аэродинамическая модель может быть обобщена на случай высокоскоростных и высокоманёвренных самолётов с реактивной силовой установкой. Для этого необходимо учитывать нелинейность зависимости аэродинамических коэффициентов от углов атаки и скольжения, а также их изменение с увеличением числа Маха [7]. Соответственные изменения претерпевает и модель погрешностей чувствительных элементов ИНС. Она должна включить в себя ошибки показаний гироскопов и акселерометров, вызванные неточностью масштабных коэффициентов, а также неортогональностью и перекосами установки их осей чувствительности [1], то есть все те погрешности, которые нарастают пропорционально измеряемым ускорениям и угловым скоростям летательного аппарата. Условия натурных испытаний ИНС на автомобиле не позволяют уточнить те значения вводимых в модель дополнительных параметров, которые были получены при заводской калибровке ИНС. Поэтому их остаточные величины следует считать случайными константами со статистическими характеристиками, указанными в спецификации ИНС производителем.
Выводы
В статье предложен программный комплекс полунатурного моделирования показаний датчиков бесплатформенных ИНС. В отличие от существующих средств моделирования, описанный комплекс обеспечивает автоматизированную идентификацию параметров моделей ошибок гироскопов и акселерометров ИНС, а также приёмника СНС. Кроме того, общий вид моделей ошибок выбран таким, чтобы обеспечивать наиболее адекватное представление погрешностей чувствительных элементов навигационных систем низкого и среднего классов точности. Программный комплекс успешно апробирован при испытаниях инерциального блока Honeywell HG1700.
Литература
- Salychev O. S. Applied Inertial Navigation: Problems and Solutions. – M.: BMSTU Press, 2004. – 304 p.
- INS Toolbox 3.0 for MATLAB. URL: http://www.navtechgps.com/ (дата обращения 14.07.2010).
- CAST-3000 Complete EGI Integration. URL: http://www.castnav.com/ (дата обращения 14.07.2010).
- Gade K. NavLab, a Generic Simulation and Post-processing Tool for Navigation // European Journal for Navigation. – Vol. 2. – Number 4. – November 2004.
- Smith, M. J., Moore, T., Hill, C. J., Noakes, C. J., Hide C. Simulation of GNSS/IMU Measurements // ISPRS International Workshop. Working Group I/5: Theory, Technology and Realities of Inertial/GPS Sensor Orientation. 22 – 23 September 2003, Castelldefels, Spain.
- Hu, C.-Y., Tsai M.-L. The Implementation of an INS-GNSS Software Simulator // Proc. of the Asian Conference on Remote Sensing, 2007.
- Миеле А. Механика полета. Том 1. Теория траекторий полета. Пер. с англ. М.: Наука, 1965. – 408 с.
- Терешков В. М. Прямой метод оценивания погрешностей датчиков бесплатформенных ИНС // Вестник МГТУ им. Н. Э. Баумана. Сер. «Приборостроение». – ╧ 3. – 2010.
- Терешков В. М. Прямой метод оценивания погрешностей датчиков инерциально-спутниковой навигационной системы // Труды ФГУП «НПЦ АП». – ╧ 2. – 2010.
- Салычев О. С. Волновое описание возмущений в задачах оценки ошибок инерциальных систем навигации. – М.: Машиностроение, 1992. – 216 с.
- HG1700 Inertial Measurement Unit. URL: http://www.honeywell.com/ (дата обращения 14.07.2010).
Публикации с ключевыми словами: моделирование, идентификация, инерциальная навигация
Публикации со словами: моделирование, идентификация, инерциальная навигация
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||