научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2009
УДК 621. 436. 054
Программа выполняет моделирование действительных термодинамических процессов в цилиндре ДВС. В результате моделирования определяются индикаторный КПД, индикаторная работа и работа насосных ходов, расход газов во впускных и выпускных клапанах или окнах, в турбине и компрессоре, эффективная мощность, расход топлива, КПД и другие показатели эффективности двигателя. Программа позволяет определить ненаблюдаемые параметры процессов, например температуру газов в цилиндре, скорость газов в окнах, в клапанах.
Программа обеспечивает ряд условий, ускоряющих решение задачи: выполняется условие ре = const, которое одновременно означает Ре = const, что обычно при выполнении оптимизационных задач; одновременно с условием ре = const выполняется условие рmax=const.
Вычислительный цикл в программе равен продолжительности термодинамического цикла, численное интегрирование дифференциальных уравнений термодинамики выполняется методом Эйлера. По завершении каждого цикла проверяются условия сходимости: одно определяет выполнение условия ре= const, вторым является условие цикличности процессов двигателя по трем параметрам. Последнее условие позволяет принимать начальные условия, не придавая большого значения их точности.
Программа VIS использует математическую модель действительных термодинамических процессов в ДВС.
В состав математической модели входят основные уравнения термодинамики, алгебраические уравнения граничных условий, эмпирические коэффициенты и физические константы, балансовые уравнения, определяющие показатели эффективности цикла и двигателя.
В математической модели реализован термодинамический метод, в котором пространство цилиндра поршневого двигателя, трубопроводов и ресиверов его систем впуска и выпуска рассматривают в общем случае как открытую термодинамическую систему, состав рабочей газовой смеси которой непрерывно изменяется (процессы сгорания и газообмена), и как закрытую ТС в процессах сжатия и расширения. Принимают, что рабочая газовая смесь находится в идеально-газовом состоянии.
Внутреннюю энергию рабочей газовой смеси определяют с учётом зависимости теплоёмкости от температуры и состава газовой смеси.
Закон тепловыделения задают в математической модели эмпирическим уравнением Вибе, которое включает экспоненту с двумя эмпирическими коэффициентами. Уравнение в интегральной форме имеет вид:
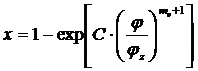 (1)
(1)
Граничные условия определяются условиями обмена массой и теплотой рассматриваемой простой термодинамической системы с окружающей средой и с другими частями сложной термодинамической системы. Они выражены уравнениями граничных условий и распределением термодинамических параметров состояния на границах.
Теплоотдачу в стенки деталей, образующих камеру сгорания, определяют по уравнению Ньютона-Рихмана при допущении о неизменности температуры стенки в продолжение цикла:
![]() .
.
Коэффициент теплоотдачи в стенки цилиндра по формуле Вошни:
![]() .
.
Газодинамические граничные условия представлены алгебраическими уравнениями и распределением термодинамических параметров состояния в граничных сечениях.
В расчетах расхода газов в клапанах и окнах учитывается обратное течение (заброс и обратный выброс) газов из цилиндра и в цилиндр. Принято допущение о том, что на участке канала от минимального сечения до выходного восстановления давления не происходит [1].
В состав математической модели входят эмпирические уравнения и коэффициенты. Многие из этих коэффициентов индивидуальны не только для определенной размерности двигателей, но и для отдельных двигателей. Поэтому, для того чтобы математическая модель адекватно описывала процессы, происходящие в цилиндре реального двигателя, необходима идентификация модели.
Программа позволяет рассчитывать площадь клапанной щели, которая принимается равной площади боковой поверхности круглого прямого усечённого конуса.
Для повышения точности расчета взамен расчетной используется экспериментальная диаграмма эффективных проходных сечений клапанов μƒ. Данная диаграмма получена в результате статических продувок крышек цилиндров с клапанами на специализированном газодинамическом стенде.
Одной из возможностей программы VIS является возможность определения мощности механических потерь. Механические потери удобно оценивать величиной среднего давления трения.
В математической модели предлагается использовать эмпирическое уравнение, учитывающее кроме скорости поршня давление в конце такта сжатия. Это можно объяснить следующим образом. Как известно, сила трения в кривошипно-шатунном механизме двигателя зависит не только от скорости движения пар трения, но и от давления между трущимися поверхностями. Скорости движения пар трения пропорциональны средней скорости поршня. Давление между трущимися поверхностями пропорционально давлению в цилиндре двигателя, которое определяется давлением в конце такта сжатия рс. Исходя из вышеизложенного, предлагается применять следующее уравнение:
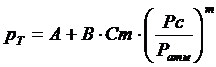 .
.
В этом уравнении три неизвестных: А, В и m. Для нахождения этих коэффициентов была решена систему из трех показательных уравнений, составленных для трех режимов работы двигателя. Для составления этих уравнений были использованы данные для двигателя 16ЧН26/26 из [2] и результаты испытания двигателя на стенде. Исходные данные для определения эмпирических коэффициентов в уравнении для определения давления механических потерь приведены в таблице.
|
n, об/мин |
Сm, м/с |
Рс, Па |
Ратм, Па |
Рт, Па |
|
1000 |
8,667 |
10149000 |
101000 |
215000 |
|
630 |
5,46 |
7804000 |
101000 |
200000 |
|
550 |
4,767 |
7348000 |
101000 |
195000 |
Данная система была решена Quasi-Newton (Квази-Ньютоновским) методом при помощи программы MathCAD. В результате уравнение для определения механических потерь имеет вид:
рт = 174796+1845.Сm.(pс/ро)0,2.
В программе VIS имеется возможность определения потерь давления во впускном устройстве компрессора. Эти потери включают в себя потери в воздушном фильтре, глушителе шума и в воздушных трубопроводах, если таковые имеются. Как известно [3], потери давления в газодинамической системе определяются выражением:
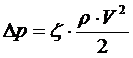 .
.
Коэффициент потерь ζ в первую очередь определяется аэродинамическим совершенством входного участка, и мало изменяется при изменении работы двигателя. Плотность воздуха на входе в компрессор ρ зависит только от температуры и давления атмосферного воздуха, и не изменяется при постоянных внешних условиях. Скорость воздуха V во входном участке компрессора прямо пропорциональна расходу воздуха через двигатель. Исходя из вышеизложенного, потери давления во входном устройстве определяются уравнением:
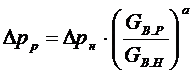 ,
,
где ![]() - потеря давления и расход воздуха на номинальном режиме,
- потеря давления и расход воздуха на номинальном режиме,
![]() - потеря давления и расход воздуха на расчетном режиме.
- потеря давления и расход воздуха на расчетном режиме.
Используя допущение о том, что коэффициент потерь ζ является постоянным, при смене режима работы двигателя, коэффициент а в уравнении для определения давления во впускном устройстве компрессора получен аналитическим путем. Запишем уравнение для расчета потерь давления на номинальном ![]() и
и ![]() расчетном режимах:
расчетном режимах:
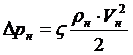 , (2)
, (2)
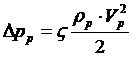 , (3)
, (3)
где: ζ, ρ, V – коэффициент потерь, плотность и скорость воздуха соответственно;
индексами «н» и «р» обозначены значения для номинального и расчетного режимов соответственно.
Разделив уравнение (3) на уравнение (2), и выразив из полученного ![]() , получим:
, получим:
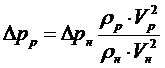 .
.
Выразив скорость из уравнения неразрывности потока, и произведя сокращения плотностей и площадей, окончательно имеем:
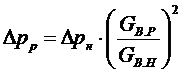 .
.
Исходя из вышеизложенного, коэффициент а в уравнении для расчета потерь давления во впускном устройстве компрессора принимается равным а=2.
Программа VIS позволяет рассчитывать параметры системы воздухоснабжения, в том числе потери давления в охладителе наддувочного воздуха. По результатам испытаний двигателя известны параметры надувочного воздуха за компрессором ТК и за ОНВ, что позволяет экспериментально получить гидравлические потери. В этом случае весь ОНВ рассматривается как одно местное сопротивление, коэффициент сопротивления которого определяется выражением:
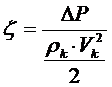 ;
;
где ![]() Р – потери полного давления в ОНВ;
Р – потери полного давления в ОНВ;
ρк – плотность воздуха за компрессором;
Vк – скорость воздуха в том же сечении.
Значения плотности и скорости воздуха во входной горловине патрубка ОНВ определяются по уравнениям состояния и неразрывности соответственно.
Коэффициент сопротивления зависит от режима течения, поэтому для применения значений ![]() на различных режимах работы двигателя необходимо знать число Рейнольдса Re.
на различных режимах работы двигателя необходимо знать число Рейнольдса Re.
Накопленный на ОАО «Коломенский завод» опыт показал, что в широком диапазоне изменения чисел Rе значение ζ остается постоянным. Поэтому потери давления в ОНВ на любом режиме можно определить через известный перепад давлений на номинальном (или каком-нибудь другом определенном) режиме.
На номинальном режиме работы двигателя известны:
массовый расход воздуха Qair н ;
давление воздуха за компрессором Рk н ;
температура воздуха за компрессором Тk н .
По известному значению ζ определяются гидравлические потери на номинальном режиме:

Для другого промежуточного режима работы двигателя:
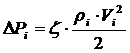 =
=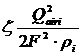 .
.
Таким образом, гидравлические потери на любом i режиме:
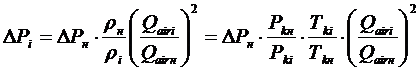 .
.
При расчете процесса сгорания в программе VIS используется уравнение Вибе (1). Как и иные эмпирические уравнения закона тепловыделения, оно представляет собой способ приближенного описания экспериментальной зависимости аналитической функцией. Уравнение Вибе содержит два эмпирических коэффициента – показатель качества сгорания mv и продолжительность сгорания ![]() . Уравнение также содержит постоянную С. Значения коэффициентов mv и
. Уравнение также содержит постоянную С. Значения коэффициентов mv и ![]() определяют обработкой индикаторных диаграмм и результатов стендовых испытаний двигателей [4]. Постоянную С находят из уравнения
определяют обработкой индикаторных диаграмм и результатов стендовых испытаний двигателей [4]. Постоянную С находят из уравнения ![]() , которое получается из (1), если φ=φZ, тогда х=xZ. Условное окончание сгорания определяется заданным значением доли выделившейся теплоты xZ. Хорошее совпадение с опытными данными можно получить, если постоянную С и продолжительность сгорания
, которое получается из (1), если φ=φZ, тогда х=xZ. Условное окончание сгорания определяется заданным значением доли выделившейся теплоты xZ. Хорошее совпадение с опытными данными можно получить, если постоянную С и продолжительность сгорания ![]() определить, принимая условно, что выделение теплоты заканчивается в точке xZ=0,95. В этом случае
определить, принимая условно, что выделение теплоты заканчивается в точке xZ=0,95. В этом случае ![]() .
.
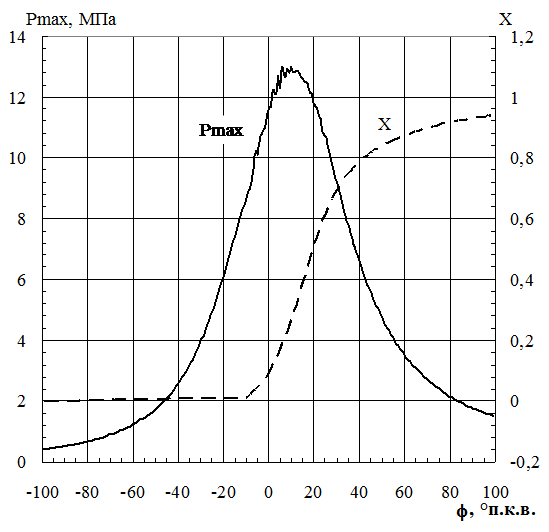
Для нахождения коэффициентов mv и ![]() проведен анализ индикаторной диаграммы, представленной на рис. 1. Диаграмма получена на двигателе 16ЧН26/26 на режиме с мощностью двигателя Ре=3330 кВт при частоте вращения коленчатого вала двигателя n=1000 об/мин. Условное окончание сгорания принято при значением доли выделившейся теплоты xZ=0,95. Как видно из рисунка 3.4, продолжительность сгорания при этом составляет
проведен анализ индикаторной диаграммы, представленной на рис. 1. Диаграмма получена на двигателе 16ЧН26/26 на режиме с мощностью двигателя Ре=3330 кВт при частоте вращения коленчатого вала двигателя n=1000 об/мин. Условное окончание сгорания принято при значением доли выделившейся теплоты xZ=0,95. Как видно из рисунка 3.4, продолжительность сгорания при этом составляет ![]() =110° п.к.в.
=110° п.к.в.
|
|
|
Рис. 1 Диаграмма давления газа в цилиндре Pmax и относительного количества сгоревшего топлива Х. |
Продолжительность сгорания можно найти, используя выражение, представленное в [5] (значения углов в рад.):
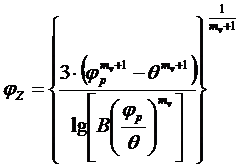 , (4)
, (4)
где θ=10° п.к.в. – угол опережения воспламенения топлива;
φр=16° п.к.в. – угол поворота коленчатого, считая от момента воспламенения до момента достижения давлением максимальной величины;
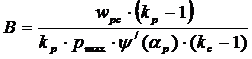 ,
,
где ![]() =118,7 кг/см2 рад – быстрота нарастания давления в момент нахождения поршня в в.м.т.
=118,7 кг/см2 рад – быстрота нарастания давления в момент нахождения поршня в в.м.т.
kp=1,351, kc=1,355 – отношение теплоемкостей в момент нахождения поршня в в.м.т. и в момент достижения давлением максимальной величины;
pmax=130 кг/см2– максимальное давление цикла;
![]() ,
,
где ε=13,5 – степень сжатия в цилиндре двигателя;
λ=0,224 – отношение радиуса кривошипа к длине шатуна;
α=6°п.к.в. – угол поворота коленчатого вала двигателя, считая от момента нахождения поршня в в.м.т. до момента достижения давлением максимальной величины.
Таким образом, из анализа индикаторной диаграммы значения всех членов уравнения (4), за исключением показателя качества сгорания mv, однозначно определяются на выбранном режиме работы двигателя. Зная величину условной продолжительности сгорания ![]() , методом подбора определяется величина mv=0,7. Таким образом окончательно принимается mv=0,7,
, методом подбора определяется величина mv=0,7. Таким образом окончательно принимается mv=0,7, ![]() =110° п.к.в.
=110° п.к.в.
Аналогичным образом была исследована индикаторная диаграмма, снятая на режиме работы двигателя n=404 об/мин и Ре=507 кВт. В результате анализа получена условная продолжительность сгорания ![]() =40° п.к.в. и показатель качества сгорания mv=0,4.
=40° п.к.в. и показатель качества сгорания mv=0,4.
Для расчета коэффициентов ![]() и mv на любом режиме в программе VIS используются зависимости, предложенные Вошни:
и mv на любом режиме в программе VIS используются зависимости, предложенные Вошни:
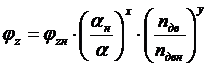 (5)
(5)
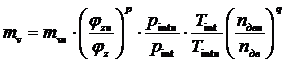 , (6)
, (6)
где: Tintн, φzн, mvн, nдвн, pintн, aн и Tint, φz, mv, nдв, pint, a – параметры двигателя на известном (номинальном) и расчетном режимах работы соответственно.
Для идентификации модели необходимо определить коэффициенты x, y, p, q. Для этого нужно решить систему минимум из двух показательных уравнений (5), составленных для разных режимов работы двигателя. Для определения коэффициентов p и q также необходимо решить систему минимум из двух показательных уравнений (6):
Для составления этих уравнений были использованы данные для двигателя 16ЧН26/26, полученные в результате обработки индикаторных диаграмм и из результатов испытаний двигателя на стенде.
Системы уравнений были решены Quasi-Newton (Квази-Ньютоновским) методом при помощи программы MathCAD. В результате получены следующие коэффициенты: x = -0,71, y = 1,04, p = -0,75, q = -0,82.
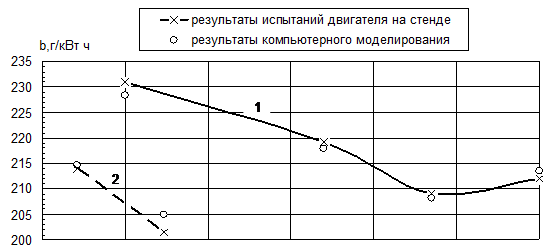
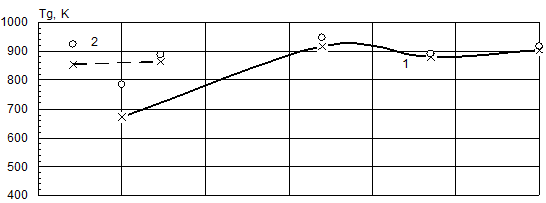
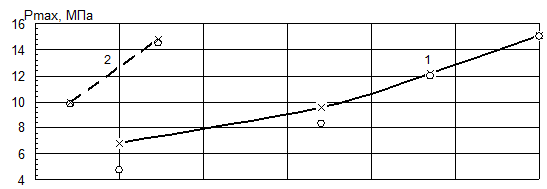
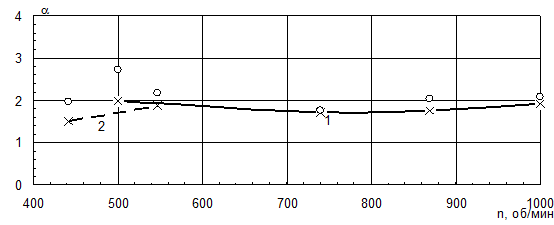
Для проверки правильности идентификации математической модели были рассчитаны четыре режима при работе двигателя по винтовой характеристике, и два – при работе по швартовной. Результаты расчета приведены на рис. 2. Для сравнения на рис. 2 нанесены результаты испытаний двигателя на стенде на соответствующих режимах. Как видно из графиков, приведенных на рисунке 2, наблюдается хорошая сходимость результатов расчета и опытных данных по удельному эффективному расходу топлива во всем диапазоне работы двигателя. По остальным параметрам в области высоких частот вращения коленчатого вала сходимость хорошая. При снижении частоты расхождение расчетных и экспериментальных данных увеличивается. Этому способствует не только неточность идентификации математической модели, но и относительная погрешность измерений, которая, как известно, минимальна при номинальной величине измеряемого параметра.
Таким образом можно сделать следующий вывод о том, что в результате идентификации математической модели подобраны эмпирические уравнения и коэффициенты, применение которых дает хорошую сходимость расчетных и экспериментальных данных.
|
|
|
Рис. 2 Результаты идентификации математической модели. 1 – винтовая характеристика, 2 – швартовная характеристика. |
Литература:
1. Иващенко Н. А., Ивин В. И. Термодинамическая оптимизация двигателя внутреннего сгорания в курсовых и дипломных работах и проектах. М.: Издательство МГТУ им. Н. Э. Баумана, 1999. 32 с.
2. Меден А. И. Исследование механических потерь в дизелях типа Д49. Диссертация на соискание ученой степени к. т. н. Коломна 1973 г.
3. Идельчик И. Е. Справочник по гидравлическим сопротивлениям. М.: Машиностроение, 1975. 559 с.
4. Вибе И.И. Новое о рабочем цикле двигателей. Москва – Свердловск, Машиздат.1962г. 272 с.
5. Петриченко Р.М., Оносовский В.В. Рабочие процессы поршневых машин. Л., Машиностроение. 1972 г. - 168 с.
Публикации с ключевыми словами: математическая модель, двигатель, эмпирические уравнения.
Публикации со словами: математическая модель, двигатель, эмпирические уравнения.
Смотри также:
- Математическая модель двигателя и трансмиссии, работающих в сотаве силовой установки транспортного средства
- Опыт создания лабораторного стенда для исследования рабочего процесса поршневого насоса
- 77-30569/362645 Выявление и анализ организационно-технологических факторов, влияющих на результативность технологических систем, организованных на основе концентрации обрабатывающих и сборочных процессов
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||