научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2009
УДК 004.3 +519.6
МГТУ им. Н.Э. Баумана
При разработке и/или анализе сложных программ достаточно часто возникает необходимость осуществить эквивалентное преобразование структуры уже имеющегося алгоритма [1-5 и др.]. Такие преобразования могут осуществляться с целью приведения алгоритмов к структурному виду, для последующего их распараллеливания, а также для распознавания типовых алгоритмических фрагментов при автоматическом анализе текстов программ.
В процессе преобразования выполняется эквивалентная замена одного фрагмента алгоритма другим. Эквивалентность преобразования предполагает, что алгоритмы, полученные после каждой замены, должны быть эквивалентны исходным в том смысле, что, сохраняя принципиальную разрешимость задачи, для каждого входа из одной и той же области определения результаты работы исходного и преобразованного алгоритмов должны совпадать.
В качестве модели алгоритма в настоящей работе будет использоваться графовая модель, предложенная в [5]. Эта модель отличается тем, что ее базис помимо вершин, соответствующих операторам обработки данных и ветвления, включает также вершины, соответствующие слиянию потоков управления. Такое слияние может быть вызвано завершением ветвления, замыканием циклической конструкции или выполнением оператора безусловной передачи управления.
Выполнение оператора ветвления приводит к тому, что множество возможных комбинаций значений данных для дальнейшей обработки делится на два: для элементов одного из них предикат условия принимает значение «истина», для элементов другого – «ложь». Слияние, в свою очередь, означает, что объединяемые множества комбинаций значений данных далее будут обрабатываться одинаково.
Следовательно, в зависимости от включенных во фрагмент операторов идентичность обработки будет интерпретироваться по-разному: для операторов ветвления – как совпадение множеств комбинаций значений данных, при которых происходит передача управления на соответствующие выходы фрагмента; для операторов изменения данных – как выполнение одинаковых преобразований данных. При наличии во фрагменте обоих типов оператор должны удовлетворяться оба критерия. При слиянии потоков управления обработки данных не выполняется, а потому отдельной трактовки идентичности обработки не требуется.
Для расширения класса решаемых задач базовый набор преобразований должен включать преобразования как логической, так и физической структур алгоритма. Для преобразования логической структуры, определяемой соответствием между результатом вычисления условия и определенной передачей управления, достаточно одного преобразования, которое позволит менять условие передачи управления и константы переходов на инверсные.
1. Инверсия условий передачи управления.
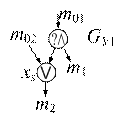
Данное преобразование может понадобиться для согласования условия выхода из цикла с типом цикла. В основу преобразования инверсии условий положим аксиому А2 из [5] – см. рис. 1.

Рис. 1. Эквивалентные куски уграфа при инверсии условия передачи управления
Очевидно, что преобразование, базирующееся на указанной аксиоме, приводит к изменению только логической структуры алгоритма, которая в данном случае определяется сопоставлением значения некоторого предиката pk значениям логических переменных
![]() ,
,
соответствующих альтернативным передачам управления (см. рис. 2, а).

Рис. 2. Преобразование «Инверсия условий передачи управления»:
а – модель исходного фрагмента; б – модель преобразованного фрагмента
Исходный GУ1 и полученный G¢У1 куски уграфа эквивалентны, если во всех возможных реализациях для этих кусков совпадают множества комбинаций значений данных, при которых осуществляются передачи управления на метки m1, m2:

где Z(m1), Z¢(m1), Z(m2), Z¢(m2) – множества комбинаций значений данных, при которых происходит передача управления на указанную метку в исходном и преобразованных фрагментах алгоритма.
Причем, если управление было передано на метку m0, то оно обязательно будет передано на метку m1 или на метку m2:
Z(m1) È Z(m2) = Z¢(m1) È Z¢(m2) = Z(m0), (2)
Z(m1) Ç Z(m2) = Z¢(m1) Ç Z¢(m2) = Æ, (3)
где Z(m0) – множество комбинаций значений данных, при которых происходит передача управления на метку m0. С учетом (1) – (2) для эквивалентности кусков уграфа достаточно выполнения любого равенства из условия (3).
В соответствии со схемами фрагментов
Z(m1) = {z(m0): bk1 « pk},
Z¢(m1) = {z(m0): b¢k1 « p¢k},
где pk, p¢k – предикаты условий вершин ветвлений исходного и полученного кусков уграфа; bk1, bk2, …Î {true, false} – логические переменные, совпадение значений которых с результатами вычисления предикатов условий приводит к осуществлению соответствующих переходов.
Совпадение множеств комбинаций значений данных, при которых происходит передача управления на указанные метки, для единственного входного потока обеспечивается тождественностью условий передачи управления на эти метки в обоих уграфах. Так для метки m1 получаем:
![]()
Из (4) окончательно получаем, что преобразование эквивалентно, если

Первое условие тривиально, оно означает, что куски уграфа эквивалентны, если предикаты условий и переменные переходов совпадают. Второе – определяет, что при изменении переменных переходов на инверсные, предикат также должен быть изменен на инверсный или, что то же самое, при изменении предиката на инверсный, переменные переходов также должны быть изменены на инверсные.
При изменении физической структуры может потребоваться поменять местами любые две из указанных вершин уграфа (управляющего графа) (см. таблицу 1).
Таблица 1
╧ | Переставляемые элементы алгоритма | Модель исходного фрагмента | Влияние на последовательность обработки данных | Примечание |
1 | Оператор изменения данных – оператор изменения данных |
| Меняет последовательность обработки данных | Возможность преобразования определяется отсутствием зависимости по данным. Структура алгоритма не меняется. |
2 | Оператор изменения данных – оператор ветвления |
| Меняет последовательность обработки данных | Предполагает внесение оператора изменения данных в ветвление или проверку условия выхода из цикла до изменения данных. |
3 | Оператор изменения данных – точка слияния |
| Не меняет последовательность обработки данных | Не структурирующее преобразование. |
4 | Оператор ветвления – оператор изменения данных |
| Меняет последовательность обработки данных | Вынесение оператора изменения данных из ветвления или изменение данных до выхода из цикла. |
5 | Оператор ветвления – оператор ветвления |
| Меняет последовательность обработки данных | Изменение последовательности ветвления потоков. |
Таблица 1 (окончание)
╧ | Переставляемые элементы алгоритма | Модель исходного фрагмента | Влияние на последовательность обработки данных | Примечание |
6 | Оператор ветвления – точка слияния |
| Не меняет последовательность обработки данных | Вынесение начала ветвления или условия выхода из цикла из конструкции ветвления. |
7 | Точка слияния – оператор изменения данных |
| Не меняет последовательность обработки данных | Расщепление потока управления в точке слияния. |
8 | Точка слияния – оператор ветвления |
| Не меняет последовательность обработки данных | Расщепление потока управления в точке слияния. |
9 | Точка слияния – точка слияния |
| Не меняет последовательность обработки данных | Изменение последовательности слияния потоков. |
Перестановка операторов или меток в большинстве случаев приводит к получению алгоритма, отличного от исходного, поэтому для каждого преобразования необходимо построить заменяющий фрагмент и сформулировать условия эквивалентности. Начнем со сравнительно простых преобразований.
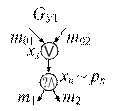
2. Изменения последовательности слияния потоков управления.
Данное преобразование (см. рис. 3) может применяться и к конструкциям ветвления и к конструкциям циклов и к их комбинациям.

Рис. 3. Преобразование «Изменения последовательности слияния потоков управления»
Преобразование не затрагивает операторов изменения данных и вычисления условий, а потому не влияет на результаты вычислений независимо от конструкций, к которым относятся соответствующие вершины слияния, т. е.:
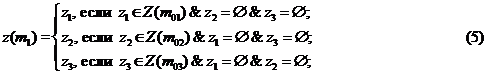

где z(m1), z¢(m1) – комбинации (n-ки) значений данных на выходе, полученные в процессе вычислений по исходному и преобразованному алгоритмам в конкретных реализациях; zi – комбинация значений данных на одном из входов фрагмента алгоритма (m01 или m02 или m03 в зависимости от реализации) в силу несовместности событий передачи управления на эти входы в конкретной реализации;Z(mk) – множества комбинаций значений данных в указанных точках алгоритма, полученных во всех возможных реализациях, причем Z(m01) È Z(m02) È Z(m03) = Z(m1).
Из (5) – (6) получаем, что
"zi Î{Z(m01), Z(m02), Z(m03)} z(m1) = z¢(m1),
т. е. преобразование эквивалентно на всех комбинациях исходных данных.
3. Вынесение начала ветвления или условия выхода из цикла из конструкции ветвления.
Преобразование (см. рис. 4) позволяет вынести начало ветвления или условие выхода из цикла – вершину xn из ветвления, завершающегося вершиной xs. Если дуга, проходящая через метку m02, замыкает цикл, то фрагмент всегда структурен.
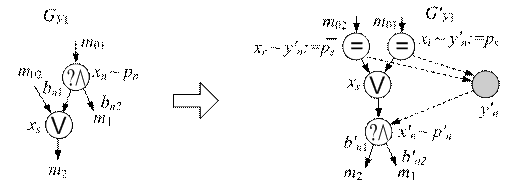
Рис. 4. Преобразование «Вынесение начала ветвления или условия выхода из цикла из конструкции ветвления»
Исходный GУ1 и полученный G¢У1 куски уграфа эквивалентны, если во всех возможных реализациях для этих кусков совпадают множества комбинаций значений данных, при которых осуществляются передачи управления на метки m1, m2:
![]()
где Z(m1), Z¢(m1), Z(m2), Z¢(m2) – множества комбинаций значений данных, при которых происходит передача управления на указанную метку в исходном и преобразованных фрагментах алгоритма.
Аналогично преобразованию 1, если управление было передано на метки m01 или m02, то оно обязательно будет передано на метку m1 или на метку m2:
Z(m1) È Z(m2) = Z¢(m1) È Z¢(m2) = Z(m01) ÈZ(m02), (8)
Z(m1) Ç Z(m2) = Z¢(m1) Ç Z¢(m2) = Æ, (9)
где Z(m01) и Z(m02) – множества комбинаций значений данных, при которых происходит передача управления на метки m01 или m02, причем события передачи управления на эти метки не совместны. С учетом (8) – (9) для эквивалентности кусков уграфа достаточно выполнения любого равенства из условия (7).
Множество комбинаций значений данных, при которых происходит передача управления на метку m1, в исходном и в преобразованном графе определяется следующим образом:
Z(m1) = {z(m01): pn « bn2}, (10)
Z(m1) = {z(m01): p¢n « b¢n2}È{z(m02): p¢n « b¢n2}, (11)
где pn, p¢n – предикаты условий вершин ветвления исходного и результирующего уграфов; bn1, bn2, …Î {true, false} – логические переменные, совпадение значений которых с результатами вычисления предикатов условий приводит к осуществлению соответствующих переходов.
Из (10–11) получаем, что
![]()
Откуда

Из (12) следует, что предикат p¢n для наборов Z(m01) и Z(m02) принимает различные значения, поэтому вычисление значений p¢n будем осуществлять в соответствующих ветвях алгоритма (см. вершины xr и xi) и записывать полученное значение в дополнительную память (вершина y¢n графа данных, соответствующая добавленной переменной).
4. Разделение потока управления в точке слияния, за которой следует оператор изменения данных.
Данное преобразование может использоваться как для ветвлений, при необходимости разделить ветви, так и для циклов, если необходимо вынести оператор изменения данных из цикла. Оно предполагает разделение обработки комбинаций значений данных, приходящих через входы m01 и m02. Обработка выполняется оператором изменения данных (см. рис. 5).

Рис. 5. Преобразование «Разделение потока управления в точке слияния,
за которой следует оператор изменения данных»
Исходный GУ1 и преобразованный G¢У1 куски уграфа эквивалентны, если любая комбинация данных исходных данных соответствующими фрагментами алгоритмов преобразуется одинаково:
![]() ,
,
где z(mk)ÎZ(mk), z¢(mk) ÎZ¢(mk) – комбинации значений данных на выходах исходного и преобразованного фрагментов соответственно;
Z(mk), Z¢(mk) – множество комбинаций значений данных, полученных в указанном месте алгоритма во всех возможных реализациях соответственно исходного и преобразованного фрагментов;
Z(m01), Z (m02) – множество комбинаций значений данных, поступающих на соответствующие входы, причем поступление данных на эти входы – события не совместные.
Соответствие комбинаций данных обеспечивается идентичными последовательностями преобразований для любых комбинаций данных.
Определим z(m1) и z¢(m1):


Откуда следует эквивалентность преобразования при любых исходных данных.
5. Разделение потока управления в точке слияния, за которой следует оператор ветвления.
Данное преобразование может использоваться как для ветвлений, при необходимости разделить ветви, так и для циклов, если необходимо вынести оператор ветвления из цикла. Оно предполагает разделение обработки комбинаций значений данных, приходящих через входы m01 и m02. Обработка выполняется оператором ветвления (см. рис. 6).
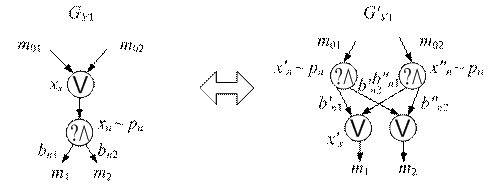
Рис. 6. Преобразование «Разделение потока управления в точке слияния, за которой следует оператор ветвления»
Исходный GУ1 и преобразованный G¢У1 куски уграфа эквивалентны, если во всех возможных реализациях для этих кусков совпадают множества комбинаций значений данных, при которых осуществляются передачи управления на метки m1, m2:

где Z(m1), Z¢(m1), Z(m2), Z¢(m2) – множества комбинаций значений данных, при которых происходит передача управления на указанную метку в исходном и преобразованных фрагментах алгоритма.
Аналогично преобразованиям 1 и 3, если управление было передано на метки m01 или m02, то оно обязательно будет передано на метку m1 или на метку m2:
Z(m1) È Z(m2) = Z¢(m1) È Z¢(m2) = Z(m01) ÈZ(m02), (14)
Z(m1) Ç Z(m2) = Z¢(m1) Ç Z¢(m2) = Æ, (15)
где Z(m01) и Z(m02) – множества комбинаций значений данных, при которых происходит передача управления на метки m01 или m02, причем события передачи управления на эти метки не совместны.
С учетом (14) – (15) для эквивалентности кусков уграфа достаточно выполнения любого равенства из условия (13).
Множество комбинаций значений данных, при которых происходит передача управления на метку m1, в исходном и в преобразованном графе определяется следующим образом:
Z(m1) = {z(m0): pn « bn1}, (16)
Z¢(m1) = {z(m01): pn « bn1}È{z(m02): pn « bn1},
где pn – предикат условия вершины ветвления уграфа;
bn1, bn2, …Î {true, false} – логические переменные, совпадение значений которых с результатами вычисления предикатов условий приводит к осуществлению соответствующих переходов.
С учетом того, что в (16) z(m0) Î Z(m01) ÈZ(m02) – элемент объединенного множества комбинаций значений данных, поступающих через оба входа, получаем, что преобразование эквивалентно при любых исходных данных.
6. Изменение последовательности ветвления потоков управления.
При преобразовании меняется порядок разделения множества комбинаций значений данных на входе на три множества, передаваемые на различные выходы (см. рис. 7), т. е. последовательность вычисления предикатов ветвлений, хотя сами данные во фрагменте не меняются.

Рис. 7. Преобразование «Изменение последовательности ветвления потоков управления»
Исходный GУ1 и полученный G¢У1 куски уграфа эквивалентны, если во всех возможных реализациях для этих кусков совпадают множества комбинаций данных, при которых осуществляются передачи управления на метки m1, m2 и m3:

где Z(mk), Z¢(mk) – множества комбинаций значений данных, при которых происходит передача управления на соответствующие метки в исходном и преобразованном фрагментах. С учетом того, что, как и в предыдущих случаях,
Z(m1) È Z(m2) È Z(m3) = Z(m0),
Z(m1) Ç Z(m2) = Z(m2) Ç Z(m3) = Z(m1) Ç Z(m3) = Æ,
для эквивалентности кусков уграфа достаточно выполнения любых двух равенств из условия (17).
Множество комбинаций значений данных, при которых происходит передача управления на метку m3 в исходном и в преобразованном фрагментах, определяется следующим образом:
Z(m3) = {z(m0): (pk « bk2)&(pn « bn2)},
Z¢(m3) = {z(m0): p¢kn « b¢n2},
где pr – предикат условия соответствующей вершины ветвления уграфа;
br1, br2, …Î {true, false} – логические переменные, совпадение значений которых с результатами вычисления предикатов условий приводит к осуществлению соответствующих переходов;
z(m0)Î Z(m0) – комбинация значений данных на входе фрагментов.
Откуда, переходя к тождественности условий передачи управления на метку m3, получаем условие эквивалентности кусков уграфа:
![]() ,
,
или окончательно:
 .
.
Аналогично для метки m1
Z(m1) = {z(m0) Î Z(m0): (pk « bk1)}, (18)
Z¢(m1) = {z Î Z(m0)\Z(m3): (pk « bk1)}, (19)
Для комбинаций значений данных Z(m3) в исходной схеме значение предиката pk « bk2. Но bk2 = ![]() , следовательно, для комбинаций значений данных Z(m3) условие pk « bk1 не выполняется и эти комбинации из Z(m0) в (3.27) можно исключить, записав вместо Z(m0) выражение Z(m0)\Z(m3).
, следовательно, для комбинаций значений данных Z(m3) условие pk « bk1 не выполняется и эти комбинации из Z(m0) в (3.27) можно исключить, записав вместо Z(m0) выражение Z(m0)\Z(m3).
Тогда выражения (18) и (19) становятся идентичными, подтверждая эквивалентность выполняемого преобразования.
7. Вынесение оператора изменения данных из ветвления или изменение данных до выхода из цикла.
В результате преобразования (см. рис. 8) происходит выделение структурной конструкции ветвления, включающей указанный оператор.
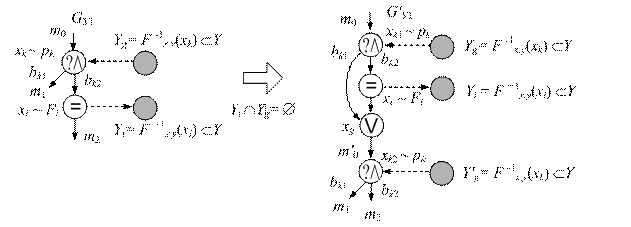
Рис. 8. Преобразование «Вынесение оператора изменения данных
из ветвления или изменение данных до выхода из цикла»
Исходный GУ1 и преобразованный G¢У1 куски уграфа на рисунке 8 эквивалентны, если любая комбинация данных соответствующими фрагментами алгоритмов обрабатывается одинаково. При наличии во фрагменте, как оператора изменения данных, так и оператора ветвления одинаковая обработка означает, что на выходах фрагментов совпадают как наборы значений, так и сами значения, т. е.:

где z(mk)ÎZ(mk), z¢(mk) ÎZ¢(mk) – комбинации значений данных на выходах исходного и преобразованного фрагментов соответственно;Z(mk), Z¢(mk) – множество комбинаций значений данных, полученных в указанном месте алгоритма во всех возможных реализациях исходного и преобразованного фрагментов, причем с учетом того, что, как и в предыдущих случаях,
Z(m1) È Z(m2) = Z(m0), Z(m1) Ç Z(m2) = Æ.
для выполнения второго условия выражения (20) достаточно выполнения одного любого равенства из этого условия.
Определим z(m1), z(m2) и z¢(m1) z¢(m2):
 ,
,
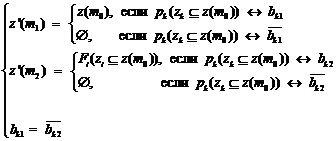 .
.
Т. е. при любых исходных данных комбинации на выходах фрагментов равны.
Теперь определим множество комбинаций значений данных, при которых управление передается на метку m1:
Z(m1) = {z(m0)ÎZ(m0): (pk (zk Í z(m0)) « bk1)}, (21)
Z¢(m1) = {z(m0)ÎZ(m0): (pk (z¢k Í z(m¢0)) « bk1)}, (22)
где zk Í z(m0) и z¢k Í z(m¢0) – аргументы предиката условия вершины ветвления в исходном и преобразованных фрагментах.
Из (21) – (22) следует, что Z(m1) = Z¢(m1), если zk = z¢k ,
т. е. после выполнения фрагмента операторов изменения данных, соответствующих вершине xi, значения аргументов предиката условия не меняются. Это возможно только, если множество результатов фрагмента операторов изменения данных Yi, соответствующих вершине xi, и множество аргументов предиката условия Yg не пересекаются: Yi Ç Yg = Æ.
Таким образом, данное преобразование получается ограниченно применимым. Однако его можно сделать тождественным, если повторно не вычислять предикат, запомнив предыдущее значение z¢¢k в дополнительной памяти y¢k (см. рис. 9).

Рис. 9. Тождественный вариант преобразования
В этом случае (22) будет записываться как
Z¢(m1) = {z(m0)ÎZ(m0): (pk (zk Í z(m0)) « bk1)},
и преобразование станет эквивалентным при любых исходных данных.
8. Внесение оператора изменения данных в ветвление или проверка условия выхода из цикла до изменения данных.
Внесение оператора изменения данных в ветвление или перенесение его за проверку условия выхода из цикла требует дублирования этого оператора и добавления его копий в обе ветви (см. рис. 10).

Рис. 10. Преобразование «Внесение оператора изменения данных в ветвление или проверка условия выхода из цикла до изменения данных»
Аналогично предыдущему преобразованию, исходный GУ1 и преобразованный G¢У1 куски уграфа эквивалентны, если любая комбинация данных соответствующими фрагментами алгоритмов обрабатывается одинаково. При наличии во фрагменте, как оператора изменения данных, так и оператора ветвления одинаковая обработка означает, что на выходах фрагментов совпадают как наборы значений, так и сами значения, т. е.:

где z(mk)ÎZ(mk), z¢(mk) ÎZ¢(mk) – комбинации значений данных на выходах исходного и преобразованного фрагментов соответственно;
Z(mk), Z¢(mk) – множество комбинаций значений данных, полученных в указанном месте алгоритма во всех возможных реализациях исходного и преобразованного фрагментов, причем с учетом того, что, как и в предыдущих случаях,
Z(m1) È Z(m2) = Z(m0),
Z(m1) Ç Z(m2) = Æ,
для выполнения второго условия выражения (23) достаточно выполнения одного любого равенства из этого условия.
Определим z(m1), z(m2) и z¢(m1) z¢(m2):
![]() ,
,
![]() .
.
Т. е. при любых исходных данных комбинации на выходах фрагментов равны.
Теперь определим множество комбинаций значений данных, при которых управление передается на метку m1:
Z(m1) = {z(m0)ÎZ(m0): (pk (zk Í z(m¢0)) « bk1)}, (24)
Z¢(m1) = {z(m0)ÎZ(m0): (pk (z¢k Í z(m0)) « bk1)}, (25)
где zk Í z(m¢0) и z¢k Í z(m0) – аргументы предикатов операторов ветвления в исходном и преобразованном фрагментах.
Из (23) – (25) следует, что
Z(m1) = Z¢(m1), если zk = z¢k ,
т. е. после выполнения фрагмента операторов изменения данных, соответствующих вершине xi, значения аргументов предиката условия не меняются. Это возможно только, если множество результатов фрагмента операторов изменения данных Yg, соответствующих вершине xi, и множество аргументов предиката условия Yj не пересекаются:
Yj Ç Yg = Æ.
Заключение.
Анализ полученных условий эквивалентности преобразований показал, что при их реализации возможны следующие варианты:
1) сохраняются все возможные последовательности обработки данных во всех возможных реализациях – такие преобразования эквивалентны на всем диапазоне допустимых комбинаций данных, т. е. тождественны;
2) меняется последовательность операций анализа данных в таких фрагментах алгоритма, в которых отсутствуют операторы изменения данных, – эквивалентность таких преобразований обеспечивается изменением предикатов условий;
3) меняется порядок обработки данных во фрагментах, включающих операторы изменения данных, – эквивалентность преобразований может быть достигнута:
а) ограничением области применимости преобразования фрагментами, операторы которых не зависят по данным,
б) сохранением в дополнительных ячейках памяти копий изменяемых значений.
Таким образом, преобразования типов 1, 2 и 3б применимы независимо от связей операторов по данным, т. е. универсальны. В то же время преобразования 1-го типа не требуют модификации операторов обработки данных в отличие от преобразований 2-го типа, предусматривающих изменение предикатов, или преобразований типа 3б, использующих дополнительную память и предполагающих добавление новых операторов изменения данных. Преобразования типа 3а с рассматриваемой точки зрения назовем ограниченно применимыми.
Окончательно получаем классификацию преобразований по условиям эквивалентности, представленную на рис. 11.

Рис. 11. Классификация структурирующих преобразований по условиям эквивалентности
С точки зрения использования ресурсов, универсальные преобразования, не использующие дополнительную память, эквивалентны по вычислительной сложности, но требуют дополнительной памяти при дублировании операторов.
Тождественные преобразования, использующие дополнительную память, увеличивают и вычислительную и емкостную сложность алгоритма. Тождественные преобразования со сформированными предикатами меняют вычислительную сложность алгоритма: уменьшают или увеличивают в зависимости от конкретных предикатов и могут потребовать дополнительной памяти для записи логических функций условий в программе.
Ограниченно применимые условные преобразования требуют дополнительной памяти для дублирования операторов программы.
Литература:
1. Мартынюк В.В. Об изменении порядка выполнения операторов в операторной схеме // ЦВТ и программирование. – М.: Советское радио, 1967. – Вып. 2. – С. 67-72.
2. Ершов А.П. Современное состояние теории схем программ // Проблемы кибернетики (М.). – 1973. – Вып. 27 (4). – С. 87-111.
3. Цейтлин Г.Е. Формальная трансформация структурированных алгоритмов сортировки // Программирование. – 1985. – ╧ 2. – С. 88-100.
4. Касьянов В.Н., Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение. – СПб.: БХВ – Петербург, 2003. – 1104 с.
5. Иванова Г.С. Формальная постановка задачи структуризации алгоритмов // Вестник Московского государственного технического университета им. Н.Э. Баумана. Приборостроение. – 2005. – ╧ 3(60). – C. 64-73.
6. Овчинников В.А., Иванова Г.С. Информационно-логическая модель алгоритма // Вестник Московского государственного технического университета им. Н.Э. Баумана. Приборостроение. – 2005. – ╧ 2(59). – C. 109-121.
7. Ершов А.П. Операторные алгоритмы. III (Об операторных схемах Янова) // Проблемы кибернетики (М.). – 1968. – Вып. 20. – С. 25-43.
Публикации с ключевыми словами: алгоритмы, преобразования агоритмов
Публикации со словами: алгоритмы, преобразования агоритмов
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||