научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#6 июнь 2008
Волкоморов С.В. (студент МГТУ им. Баумана, e-mail: s.volkomorov@gmail.com)
Кветкин Г.А. (аспирант МГТУ им. Баумана, e-mail: kvetkin.g@gmail.com)
Основополагающими элементами систем автоматического управления (САУ) подвижными объектами являются инерциальные навигационные системы, чувствительными элементами которых часто выступают кольцевые лазерные гироскопы. Объектом исследования настоящей работы является виброподвес (вибрационная подставка) кольцевого лазерного гироскопа, обеспечивающий функционирование прибора в области малых угловых скоростей основания.
1. Постановка задачи
В
области высоких частот углового вращения при работе кольцевого лазерного
гироскопа зависимость разницы частот волн ![]() приходящих
лазерных лучей, от угловой скорости вращения точки закрепления
приходящих
лазерных лучей, от угловой скорости вращения точки закрепления ![]() близка к линейной
зависимости. В области низких частот существует зона нечувствительности (см.
рис. 1). Для обеспечения функционирования гироскопа в области малых угловых
скоростей его основания используются принудительные колебания этого основания.
С этой целью в конструктивную схему виброподвеса кольцевого лазерного гироскопа
включают четыре упругих стойки (торсиона), соединенных пластиной из ситалла
(см. рис. 2). На упругих стойках располагаются пьезоэлементы, с помощью которых
создаются изгибные колебания торсионов и, как следствие, крутильные колебания
ситалловой пластины, на которой располагаются оптоэлектронные компоненты
гироскопа. Подобная схема реализована в ряде отечественных разработок,
например, приборах, типа, ГЛ-2 [1,2].
близка к линейной
зависимости. В области низких частот существует зона нечувствительности (см.
рис. 1). Для обеспечения функционирования гироскопа в области малых угловых
скоростей его основания используются принудительные колебания этого основания.
С этой целью в конструктивную схему виброподвеса кольцевого лазерного гироскопа
включают четыре упругих стойки (торсиона), соединенных пластиной из ситалла
(см. рис. 2). На упругих стойках располагаются пьезоэлементы, с помощью которых
создаются изгибные колебания торсионов и, как следствие, крутильные колебания
ситалловой пластины, на которой располагаются оптоэлектронные компоненты
гироскопа. Подобная схема реализована в ряде отечественных разработок,
например, приборах, типа, ГЛ-2 [1,2].
Целью исследования является определение амплитудно-частотной характеристики (АЧХ) виброподвеса при различных значениях конструктивных параметров торсионов.
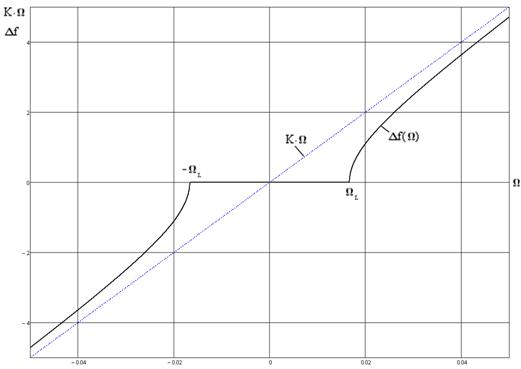
Рис. 1.
Зона нечувствительности лазерного гироскопа: 
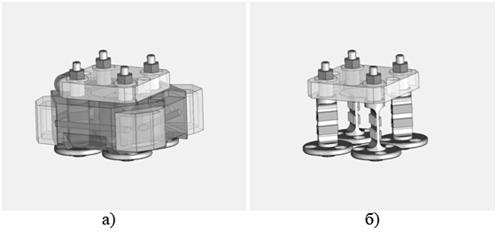
Рис. 2. Конструкция вибрационной подставки: а - вибрационная подставка в сборе; б ‑ вибрационная подставка без моноблока оптоэлектронных компонентов гироскопа.
На
основе анализа параметров существующих виброподвесов область исследования
ограничена по частоте значениями 500[Гц] – 700[Гц], а по амплитуде – значениями
![]() -
-![]() (угловых минут).
Исследованы три варианта конструкции виброподвеса, отличающиеся толщиной
рабочей части торсиона
(угловых минут).
Исследованы три варианта конструкции виброподвеса, отличающиеся толщиной
рабочей части торсиона ![]() :
:
![]() 1,7 [мм];
1,7 [мм];
![]() 1,9 [мм];
1,9 [мм];
![]() 2,1 [мм].
2,1 [мм].
В работе подготовка 3D модели виброподвеса выполняется с помощью программного комплекса Kompas, а для исследования используется программный комплекс конечно-элементного анализа ANSYS [3, 4].
2. Построение модели виброподвеса
Подготовка модели конструкции к импорту в программный комплекс ANSYS выполняется, как отмечалось выше, с помощью программного комплекса Kompas и состоит из следующих этапов:
· &n bsp; создание 3D-моделей отдельных деталей конструкции;
· &n bsp; создание сборочной 3D-модели и конвертация ее в формат, поддерживаемый программным комплексом ANSYS;
· &n bsp; импорт 3D-модели в ANSYS;
· &n bsp; задание числовых значений параметров модели (граничные условия, параметры силовых воздействий и т.п.).
Специфика разработки 3D модели виброподвеса заключается в разработке 3D моделей пьезоэлементов (пьезоактюаторов), с помощью которых создаются изгибные колебания торсионов. Поэтому остановимся на этом детальнее.
Пьезоактюатор (пьезодвигатель нано- и микроперемещений) функционирует на основе обратного пьезоэффекта - деформации пьезоэлемента при приложении внешнего электрического напряжения. Увеличение диапазона перемещений до десятков микрометров достигается при использовании блочного (составного) пьезоактюатора (см. рис. 3).
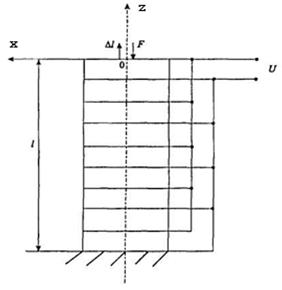
Рис. 3. Блочный пьезоактюатор при продольном пьезоэффекте: ![]() — длина пьезоактюатора;
— длина пьезоактюатора; ![]() — перемещение;
— перемещение; ![]() - входное напряжение;
- входное напряжение; ![]() - усилие.
- усилие.
Отметим, что применение простых и блочных пьезоактюаторов для нано- и микроманипуляторов позволяет решить задачи точного совмещения в микроэлектронике, нано-технологиях, астрономии и адаптивной оптике [6].
Изгибные колебания каждого из торсионов виброподвеса достигаются с помощью четырех пьезоэлементов, приклеиваемых к граням торсионов (см. рис. 4).
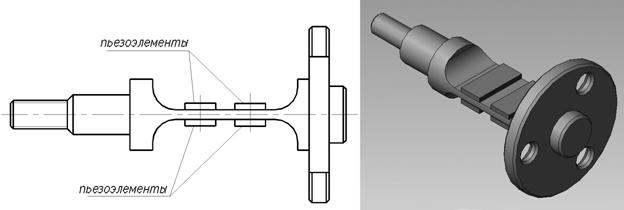
Рис. 4. Расположение пьезоэлементов на торсионе.
В простейшем случае силовое воздействие актюатора на торсионы моделируется путем приложения точечных сил (см. рис. 5). Как показывают наши исследования, в результате происходит сильное искажение физической картины деформации торсиона – имеет место «выпячивание» материала в точках воздействия (см. рис. 6).
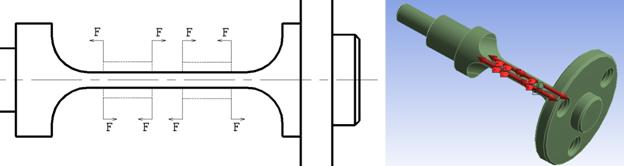
Рис. 5. Имитация действия пьезоэлемента точечными силовыми воздействиями.
В работе используется представление пьезоэлемента в виде параллелепипеда, приклеенного (без учета демпфирующих свойств клея) к граням торсиона. Усилия, создаваемые пьезоэлементами моделируются приложением эквивалентных давлений (см. рис. 7). Нами показано, что в этом случае физическая картина деформации торсиона не искажается.
3. Оптимизация конечно-элементной модели виброподвеса
Одним из наиболее важных этапов в конечно-элементном анализе является построение конечно-элементной сетки, покрывающей модель. В программном комплексе ANSYS имеется два основных метода построения сетки: построение произвольной сетки; построение упорядоченной сетки.
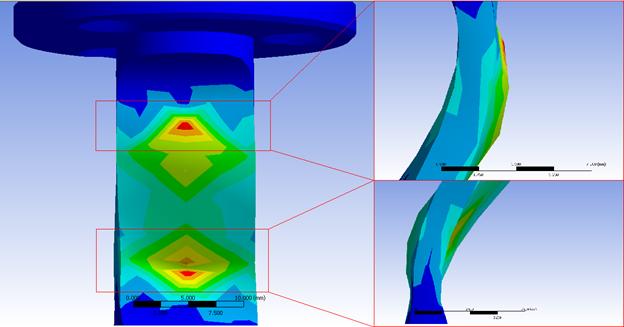
Рис. 6. Последствия представления действия пьезоэлемента точечными силовыми воздействиями.
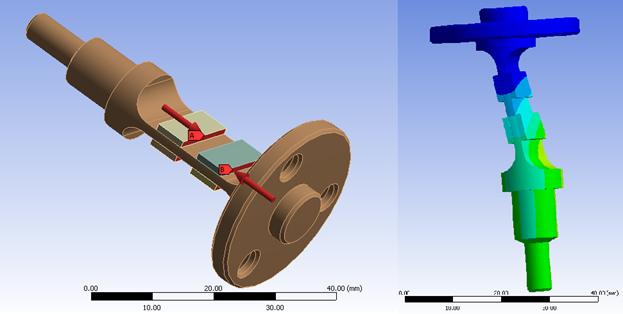
Рис. 7. Имитация действия пьезоэлемента приложением давления к граням заменяющего его параллелепипеда.
Произвольная сетка строится автоматически, при этом соседние конечные элементы могут существенно отличаться по размерам. В такой сетке при большом количестве конечных элементов число узлов преобладает над числом элементов: для плоских произвольных сеток отношение количеств узлами и конечных элементов равно, примерно, 2:1; для трехмерных произвольных сеток с четырехгранными элементами - 6:1.
Практика расчетов с применением метода конечных элементов показывает, что упорядоченная сетка является более предпочтительной, чем произвольная сетка, как с точки зрения быстродействия, так и с точки зрения точности вычислений.
Импорт в программный комплекс ANSYS 3D-модели анализируемого объекта, построенной при помощи стороннего программного продукта, иногда приводит к получению модели с особенностями геометрии, не позволяющими получить удовлетворительное качество конечно-элементной сетки. Такие особенности можно разделить на две следующие группы.
1) «Неопрятность» модели - представление окружностей в виде совокупности двух и более дуг, неоправданное разбиение плоских и криволинейных поверхностей на субповерхности (см. рис. 8) и т.д. «Неопрятность» модели приводит к возрастанию количества конечных элементов и, как следствие, к увеличению вычислительных затрат (без увеличения точности результатов). Методом борьбы с «неопрятностью» модели может служить ручное консолидирование избыточных объектов либо использование встроенной функции ANSYS Workbench – Insert Virtual Topology [3, 4].
2) Небольшие выступы на модели, приводящие к измельчению сетки в этой области. Иногда детализация конечно-элементной сетки на таких выступах оправдана, потому что они являются концентраторами напряжения. В противном случае, измельчение сетки должно устраняться выделением выступов в самостоятельные объекты и покрытием их отдельной конечно-элементной сеткой.
С целью уменьшения числа конечных элементов и регуляризации конечно-элементной сетки, при создании модели ситалловой пластины виброподвеса выступы на ее поверхности были выделены в самостоятельные объекты. Это позволило, во-первых, произвести покрытие таких выступов сеткой методом sweep (один из методов получения упорядоченной сетки) и, во-вторых, существенно снизить количество конечных элементов самой пластины за счет исключения мелкой сетки на границах выступов (см. рис. 9). Кроме этого, для оптимизации конечно-элементной сетки была применена функция Insert Virtual Topology, в результате чего поверхности с малой площадью в случае плавного перехода были присоединены к соседним поверхностям (см. рис. 9).
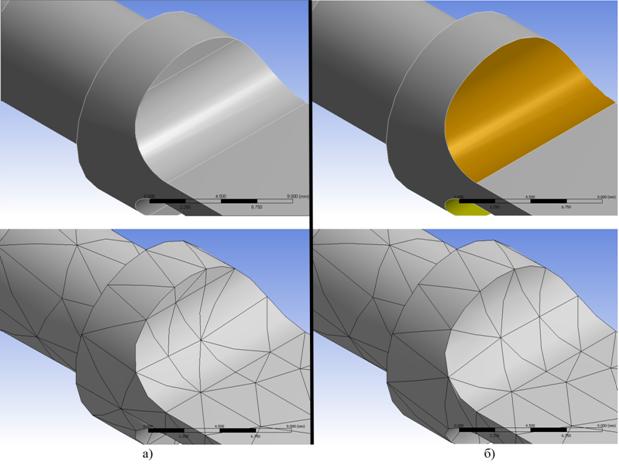
Рис. 8. Результат работы функции Insert Virtual Topology:
а – появление мелких конечных элементов на стыке избыточных субповерхностей;
б – слияние субповерхностей и результирующая сетка конечных элементов.
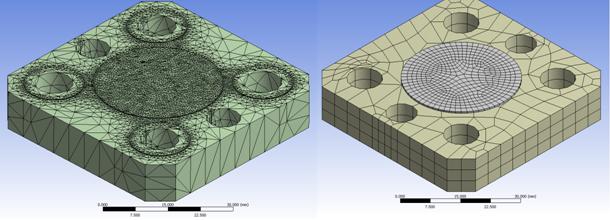
Рис. 9. Устранение избыточно мелкой сетки путем деления объемов на под-объемы.
В результате указанных мер было достигнуто уменьшение количества конечных элементов более чем втрое по сравнению с неоптимизированной моделью (~15 тысяч элементов вместо ~60 тысяч).
4. Моделирование демпфирующих свойств материала торсионов
Поскольку исследования выполнялись в областях резонансных частот торсионов, особое внимание было уделено моделированию демпфирующих свойств материала торсионов. Ввиду малой угловой амплитуды колебаний (~5’) мы пренебрегли сопротивлением воздуха и рассматривали только потери энергии на внутреннее трение в материале торсиона.
Рассеяние энергии в материале при циклической нагрузке в значительной мере и, обычно, нелинейно зависит от амплитуды колебаний, определяющей напряжения в материале, и в диапазоне исследования практически не зависит от частоты колебаний. На этом основании в модели используется коэффициент демпфирования колебаний определяемый с помощью экспериментальных зависимостей логарифмического декремента затуханий от напряжений в материале торсионов (бронза Бр.АЖ9-4) при колебаниях чистого изгиба [5].
С
помощью модального анализа (Modal
Analysis) было найдено, что
первая собственная мода виброподвеса соответствует задаваемым крутильным
колебаниям. Для этой формы колебаний с точностью до масштабного коэффициента
найдены максимальные напряжения в торсионах. Масштабные коэффициенты
рассчитаны, исходя из требуемой амплитуды крутильных колебаний ситалловой
пластины (5’). Затем на основе линейной аппроксимации зависимости ![]() (см рис. 10) для области полученных
напряжений, получены значения логарифмических декрементов затухания
(см рис. 10) для области полученных
напряжений, получены значения логарифмических декрементов затухания ![]() (см. табл. 1).
(см. табл. 1).
Таблица 1. К моделированию демпфирующих свойств материала торсионов.
|
Параметр |
Вариант расчета |
||
|
Толщина
торсиона |
1,7 |
1,9 |
2,1 |
|
Максимальное
напряжение |
66,2 |
60,9 |
60,3 |
|
Логарифмический
декремент затухания |
10,8е- 4 |
10е- 4 |
9,8е- 4 |
|
Относительный
коэффициент демпфирования |
1,71e-4 |
1,6e-4 |
1,56е- 4 |
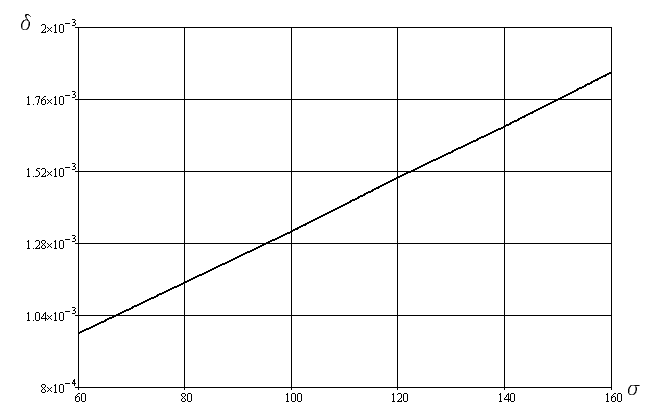
Рис. 10. Зависимость ![]() логарифмического
декремента затухания от максимального напряжения [МПа] в материале.
логарифмического
декремента затухания от максимального напряжения [МПа] в материале.
Для задания диссипации в среде ANSYS
требуется указать относительный коэффициент демпфирования ![]() (см. табл. 1). Здесь
(см. табл. 1). Здесь ![]() - коэффициент затухания,
где
- коэффициент затухания,
где ![]() – частота
демпфированных колебаний;
– частота
демпфированных колебаний;![]() – критическое значение коэффициента
затухания, при котором колебательный процесс не возникнет.
– критическое значение коэффициента
затухания, при котором колебательный процесс не возникнет.
Для нахождения ![]() рассмотрим уравнение гармонических
колебаний тела:
рассмотрим уравнение гармонических
колебаний тела:
![]()
Здесь ![]() - квадрат собственной частоты колебаний.
Решения уравнения (1) ищется в виде
- квадрат собственной частоты колебаний.
Решения уравнения (1) ищется в виде ![]() . После подстановки получим:
. После подстановки получим:
![]() .
.
Колебания возникнут, если мнимая часть
показателя степени не равна нулю. Критическим называется минимальное значение коэффициента![]() , при котором колебания
отсутствуют, т.е.
, при котором колебания
отсутствуют, т.е. ![]() .
.
Частота полученных колебаний ![]()
Для случаев небольшого демпфирования (![]() ) можно принять, что
) можно принять, что ![]() .
.
Таким образом, ![]() .
.
5. Результаты работы и их обсуждение
Основным результатом работы являются амплитудно-частотные характеристики виброподвеса, представленные на рис. 11.
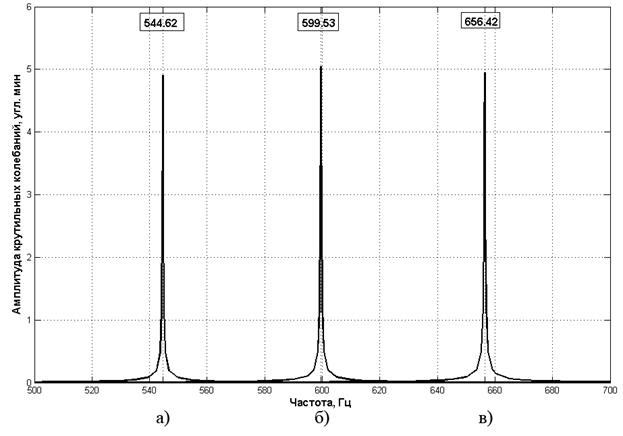
Рис. 11. АЧХ виброподвеса: а – h=1,7 [мм]; б – h=1,9 [мм]; в – h=2,1 [мм].
Для их получения использовалась функция ANSYS «Гармонический анализ» (Harmonic Response), а также метод суперпозиции мод (Mode Superposition), основанный на кластерном выборе частот (в окрестности собственной частоты вычисления производятся значительно чаще, чем для остального диапазона частот). Полученные расчетные значения собственных частот соответствуют экспериментальным данным, что говорит об адекватности используемой модели.
Изображение виброподвеса в рабочем режиме приведено на рис. 12.

Рис. 12. Виброподвес в нагруженном состоянии. Цветом показаны смещения относительно положения покоя.
Отметим, что несовпадение собственных частот при использовании различных толщин рабочей части торсионов имеет важное конструктивное значение. В реальной конструкции лазерного гироскопа используется три виброподвеса (см. рис. 13), по одному на каждую из осей координат. Разнесение собственных частот виброподвесов в этом случае необходимо во избежание одновременного возникновения у них резонанса.

Рис. 13. Лазерные гироскопы на раме.
В дальнейших исследованиях мы планируем использовать более точную модель пьезоэлемента – не в виде одной пластины, а в виде некоторого набора узких пластин. Предполагается также учет демпфирующих свойств клея, которым пьезоэлементы приклеиваются к граням торсионов.
Литература
1. Бакин Ю.В., Болотнов С.А., Людомирский М.Б., Алексейченко А.А. Лазерные гироскопы с призмами полного внутреннего отражения //Вестник МГТУ им. Н.Э.Баумана. Сер. «Приборостроение». -2007, N1, с. 97-104.
2. Болотнов С.А., Вереникина Н.М., Алексейченко А.А. Бесплатформенная инерциальная навигационная система на лазерных гироскопах //Вестник МГТУ им. Н.Э.Баумана. Сер. «Приборостроение». -2007, N3, с. 37-43.
3. Басов К.А. ANSYS: Справочник пользователя. -М.: ДМК Пресс, 2005, -640 с.
4. Каплун А.Б., Морозов Е.М., Олферьева М.А. ANSYS в руках инженера: Практическое руководство. -М.: Едиториал УРСС, 2003, -272 с.
5. Писаренко Г.С., Яковлев А.П., Матвеев В.В. Вибропоглощающие свойства конструкционных материалов. -Киев: «Наукова думка», 1971, -375 с.
6. Афонин С.М., Афонин П.С. Моделирование характеристик пьезоэлектрических блочных актюаторов для нано- и микроманипуляторов // Нано- и микросистемная техника. 2006. ╧11. C. 25-30.
Публикации с ключевыми словами: виброподвес, лазерный гироскоп, оптимизация сетки конечных элементов
Публикации со словами: виброподвес, лазерный гироскоп, оптимизация сетки конечных элементов
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



