научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#6 июнь 2008
УДК 621.31(075.8)
С. А.
Васюков,
МГТУ им. Н. Э. Баумана, кафедра ФН-7
(“Электротехника и промышленная электроника”)
Цилиндрические электростатические подвесы, работающие в среде с жидким диэлектриком, могут применяться в качестве органа точного центрирования подвижных систем разнообразных чувствительных элементов: акселерометров, наклономеров, гравиметров.
В настоящее время опубликовано много работ, посвященных расчету силовых характеристик и уводящих моментов сферических электростатических подвесов. Особо следует отметить монографию Мартыненко Ю. Г. [1], где достаточно полно проанализированы силовые характеристики сферического электростатического подвеса для различных конфигураций электродных систем. Публикации же по силовым характеристикам цилиндрических подвесов практически отсутствуют.
Расчет силовых характеристик цилиндрического подвеса имеет свою специфику, так как требует дополнительного учета ряда моментов. Необходимо рассматривать не только линейные, но и угловые смещения ротора, желательно учесть технологический разброс в зазорах левого и правого подвесов. Существуют особенности выбора закона управления потенциалами на электродах подвеса [2], при которых минимизируется наведенный потенциал ротора. В связи с этим, непосредственный перенос опыта и методик расчета сферических подвесов на цилиндрические не представляется возможным.
В представленной работе поставлена задача расчета силовых и моментных характеристик цилиндрического электростатического подвеса и определения условий, при которых возможна линеаризация характеристик. Также требуется оценить влияние неидентичности зазоров левого и правого подвесов на глубину перекрестных связей в силовых характеристиках. Для статических силовых характеристик необходимо определить предельные величины линейных и угловых смещений, при которых подвес сохраняет свои восстанавливающие свойства.
В акселерометрах, относящихся к классу поплавковых маятниковых приборов и работающих в компенсационном режиме, подвижная система, рис. 1, содержит два цилиндрических поплавка, которые служат для обеспечения гидростатической разгрузки. Поверхности поплавков используются в качестве роторов электростатических подвесов, выполняющих функции дополнительных прецизионных элементов центрирования подвижной системы.

Рис. 1. Цилиндрический электростатический подвес
Величины максимальных сил и моментов, развиваемых электростатическим подвесом, напрямую зависят от габаритных размеров поплавков и электродной системы. Однако эти размеры во многом определены условиями, заданными при проектировании прибора.
При
определенных габаритных размерах подвеса, ключевыми параметрами, влияющими на
величины максимальных сил и моментов остаются зазоры электрод-ротор ![]() и
и ![]() , а также предельная напряженность
электрического поля в жидкости
, а также предельная напряженность
электрического поля в жидкости ![]() , с которой непосредственно связана величина
максимального опорного напряжения на электродах подвеса.
, с которой непосредственно связана величина
максимального опорного напряжения на электродах подвеса.
Для уменьшения
вероятности электрического пробоя в жидкости при начальном всплытии
чувствительного элемента (ЧЭ) рекомендуется установка в приборах специальных страховочных
упоров, с которых происходит всплытие ротора. Обычно в качестве упоров
применяют камниевые опоры, рис. 1. Общий ход оси подвижной системы в упорах в
радиальном направлении ограничивается величиной ![]() , а в осевом направлении -
, а в осевом направлении - ![]() . Типовое значение общего
хода цапфы в камниевой опоре лежит в диапазоне 5…10 мкм, т.е. составляет от 7
до 30% от рекомендуемых зазоров электрод-ротор.
. Типовое значение общего
хода цапфы в камниевой опоре лежит в диапазоне 5…10 мкм, т.е. составляет от 7
до 30% от рекомендуемых зазоров электрод-ротор.
Необходимо учитывать, что из-за конструктивных особенностей приборов с цилиндрическим электростатическим подвесом (ЦЭСП) не удается обеспечить полное равенство зазоров левого и правого подвесов. Очевидно, что неидентичность зазоров отражается на силовых и моментных характеристиках.
Расчетная схема подвеса приведена на рис. 2. Взвешиваемое тело цилиндрической формы окружено системой электродов, представляющих собой тонкие металлизированные площадки, расположенные на внутренней поверхности корпуса. В принятой модели межэлектродные промежутки, располагающиеся на одной с электродами поверхности, также металлизированы и объединены в один электрод, который назовем внешним проводящим экраном. Экран изолирован от остальных электродов и его потенциал в дальнейшем принимаем равным нулю.
Присвоим ротору индекс i =
0, электродам i = 1, ….,
10, экрану i = 11. Обозначим
![]() - потенциал и
заряд i –го проводника.
- потенциал и
заряд i –го проводника.

Рис. 2. Расчетная схема цилиндрического подвеса
Тогда для системы проводников, составляющих электростатический подвес, можно записать
 j=0,..., n
(1)
j=0,..., n
(1)
где ![]() - коэффициенты
электростатической индукции, которые связывают заряды тел qi с их потенциалами
- коэффициенты
электростатической индукции, которые связывают заряды тел qi с их потенциалами ![]() . В работе [3] были получены базовые коэффициенты
электростатической индукции как функции геометрических размеров подвеса, а
также нормированных линейных
. В работе [3] были получены базовые коэффициенты
электростатической индукции как функции геометрических размеров подвеса, а
также нормированных линейных ![]() и угловых
и угловых ![]() смещений ротора. В силу ограниченности
объема данной статьи приведем лишь общую структуру базовых коэффициентов, не
раскрывая детально их отдельные составляющие
смещений ротора. В силу ограниченности
объема данной статьи приведем лишь общую структуру базовых коэффициентов, не
раскрывая детально их отдельные составляющие
 (2)
(2)
Обозначим ![]() произвольное,
малое линейное смещение оси ротора. Тогда выражение для проекции силы на
направление
произвольное,
малое линейное смещение оси ротора. Тогда выражение для проекции силы на
направление ![]() примет
вид [4]
примет
вид [4]
 (3)
(3)
Естественно предположить, что если бы мы взяли в качестве малого смещения
угловое перемещение ![]() ,
то в результате получили бы выражение для момента сил электрического поля
,
то в результате получили бы выражение для момента сил электрического поля
 (4)
(4)
Выражения (3) и (4) позволяют установить зависимость центрирующей силы и
момента подвеса от потенциалов на его электродах, которые изменяются при регулировании,
а также от параметров перемещений ротора, входящих в эти формулы через
коэффициенты ![]() .
.
Если воспользоваться преобразованиями координат, то можно на основе базовых
коэффициентов построить полный набор коэффициентов ![]() и определить проекции сил в ЦЭСП
на координатные оси. Здесь следует отметить, что, в силу симметрии подвеса, достаточно
найти выражения сил и моментов, действующих в какой-либо одной плоскости,
например xOz. Остальные проекции легко находятся
перестановкой индексов.
и определить проекции сил в ЦЭСП
на координатные оси. Здесь следует отметить, что, в силу симметрии подвеса, достаточно
найти выражения сил и моментов, действующих в какой-либо одной плоскости,
например xOz. Остальные проекции легко находятся
перестановкой индексов.
Введем коэффициенты неидентичности левого с1 и правого с2 подвесов. Если номинальный зазор при центральном положении ротора равен h, то с введенными коэффициентами, зазоры левого и правого подвесов представим в виде
![]()
![]() (5)
(5)
С учетом (5), обобщенные выражения сил и моментов, действующих в плоскости xOz, примут вид

 (6)
(6)

Проекция момента на ось z принималась равной нулю, так как в рассматриваемой модели поверхность цилиндра предполагалась идеальной.
Соотношения (6) являются функциями потенциалов на электродах, смещений ротора из центра подвеса, а также потенциала ротора.
Проанализируем силовые характеристики цилиндрического подвеса на постоянном токе. Управление в подвесах на постоянном токе осуществляется по законам [2]
![]() (7)
(7)
Здесь i, j – номера пар диаметрально противоположных электродов.
Для
цилиндрического подвеса номера пар (i, j) принимают значения (1, 2), (3, 4), (5, 6), (7, 8), (9,
10). Коэффициенты ![]() равны
плюс или минус единица. Потенциал
равны
плюс или минус единица. Потенциал ![]() является положительной величиной и
представляет собой начальную уставку или опорное напряжение на электродах.
Приращение потенциала
является положительной величиной и
представляет собой начальную уставку или опорное напряжение на электродах.
Приращение потенциала ![]() в
статическом режиме пропорционально напряжению на выходе датчика перемещений
в
статическом режиме пропорционально напряжению на выходе датчика перемещений ![]() и не превышает по абсолютной
величине потенциала уставки:
и не превышает по абсолютной
величине потенциала уставки:
 (8)
(8)
Здесь ![]() - коэффициент усиления
следящей системы, подключенной к паре электродов (i,
j).
- коэффициент усиления
следящей системы, подключенной к паре электродов (i,
j).
Коэффициенты![]() и
и ![]() подбираются таким образом, чтобы минимизировать
потенциал ротора. В работе [2] были рассмотрены несколько вариантов распределения
уставок с точки зрения минимизации потенциала ротора. Рассмотрим вариант, для
которого
подбираются таким образом, чтобы минимизировать
потенциал ротора. В работе [2] были рассмотрены несколько вариантов распределения
уставок с точки зрения минимизации потенциала ротора. Рассмотрим вариант, для
которого
![]() (9)
(9)
Проанализируем сначала случай малых смещений (работа подвеса в линейной зоне) при котором потенциалы на электродах не выходят на насыщение.
Примем ![]() т.е. по абсолютной
величине опорное напряжение на всех электродах подвеса одинаковое. Подставляя (7),
(8), (9) в (6), получим проекцию силы ЦЭСП на ось x:
т.е. по абсолютной
величине опорное напряжение на всех электродах подвеса одинаковое. Подставляя (7),
(8), (9) в (6), получим проекцию силы ЦЭСП на ось x:
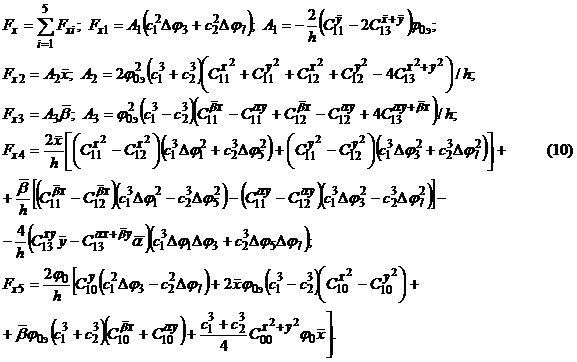
Проведем анализ отдельных составляющих силовой характеристики.
Составляющая ![]() пропорциональна
приращению потенциалов на электродах левого подвеса
пропорциональна
приращению потенциалов на электродах левого подвеса ![]() и правого подвеса
и правого подвеса ![]() , причем оси электродов,
формирующих эти приращения, совпадают с осью x. Раскроем
выражения
, причем оси электродов,
формирующих эти приращения, совпадают с осью x. Раскроем
выражения ![]() и
и ![]() . Для этого воспользуемся
соотношением (10), а также обобщенными выражениями для датчиков перемещений
цилиндрического подвеса, полученными в [2]:
. Для этого воспользуемся
соотношением (10), а также обобщенными выражениями для датчиков перемещений
цилиндрического подвеса, полученными в [2]:  (11)
(11)
где ![]() - напряжения емкостных датчиков,
подключенных к парам электродов (1, 2), (3, 4), (5, 6), (7, 8), (9, 10)
соответственно.
- напряжения емкостных датчиков,
подключенных к парам электродов (1, 2), (3, 4), (5, 6), (7, 8), (9, 10)
соответственно.
Подставляя в (8) выражения (11), получим следующие значения приращений потенциала:
![]() (12)
(12)
Здесь ![]() где
где
![]() - коэффициенты
усиления в канале регулирования, которые содержат составляющие от датчика
- коэффициенты
усиления в канале регулирования, которые содержат составляющие от датчика ![]() и от дополнительного
усилителя
и от дополнительного
усилителя ![]() радиального
канала. Используя выражение (12), запишем соотношение для составляющей
радиального
канала. Используя выражение (12), запишем соотношение для составляющей ![]() в статическом режиме:
в статическом режиме:
![]() (13)
(13)
Из (13) видно, что![]() имеет
не только полезную составляющую, пропорциональную
имеет
не только полезную составляющую, пропорциональную ![]() , но и перекрестную связь по
, но и перекрестную связь по ![]() , глубину которой можно оценить
коэффициентом
, глубину которой можно оценить
коэффициентом

При отклонении зазоров подвесов в разные стороны от номинального зазора
на 5 % коэффициент перекрестной связи ![]() принимает значение 14,9 %, если же подвесы
сделаны некачественно и отклонение составляет 10 %, то
принимает значение 14,9 %, если же подвесы
сделаны некачественно и отклонение составляет 10 %, то ![]() .
.
При ![]() перекрестная
связь исчезает и
перекрестная
связь исчезает и![]() можно
представить в виде
можно
представить в виде
![]()
где ![]() . Сила и перемещение здесь
имеют разные знаки, можно говорить о том, что
. Сила и перемещение здесь
имеют разные знаки, можно говорить о том, что![]() стремится ликвидировать смещение. В связи с
этим составляющую
стремится ликвидировать смещение. В связи с
этим составляющую ![]() будем
называть стабилизирующей.
будем
называть стабилизирующей.
В противоположность ![]() , составляющая
, составляющая ![]() всегда имеет положительную крутизну по
всегда имеет положительную крутизну по ![]() , т.е. является
дестабилизирующей составляющей. Естественно, одним из условий устойчивости
подвеса является преобладание стабилизирующей составляющей над дестабилизирующей,
т.е. должно выполняться соотношение
, т.е. является
дестабилизирующей составляющей. Естественно, одним из условий устойчивости
подвеса является преобладание стабилизирующей составляющей над дестабилизирующей,
т.е. должно выполняться соотношение ![]() . Если учесть, что
. Если учесть, что ![]() , где
, где ![]() - величина линейной зоны подвеса, на границе
которой
- величина линейной зоны подвеса, на границе
которой ![]() , то при
, то при
![]()
 (14)
(14)
Из (14) видно, что дестабилизирующая составляющая увеличивается с ростом
линейной зоны ![]() ;
с этой точки зрения наиболее выгодным является подвес с нулевой линейной зоной
(релейное управление).
;
с этой точки зрения наиболее выгодным является подвес с нулевой линейной зоной
(релейное управление).
Коэффициенты электростатической индукции, входящие в выражение (14),
сложным образом зависят от таких параметров подвеса как зазор, линейных и угловых
размеров электродов, их взаимного расположения и.т.п. и проследить аналитическую
зависимость ![]() оп
этих параметров не представляется возможным. Учитывая это, оценим влияние зазора
оп
этих параметров не представляется возможным. Учитывая это, оценим влияние зазора
![]() (как одного из
основных параметров, определяющих максимальную силу подвеса) на величину
(как одного из
основных параметров, определяющих максимальную силу подвеса) на величину ![]() для конкретных
типоразмеров опытного образца прибора с цилиндрическим подвесом (см. рис. 2):
для конкретных
типоразмеров опытного образца прибора с цилиндрическим подвесом (см. рис. 2):
![]()
Воспользовавшись
соотношениями для коэффициентов электростатической индукции, полученными в [3],
определим, что при зазоре ![]() и
и ![]() , коэффициент
, коэффициент ![]() . С ростом зазора коэффициент
. С ростом зазора коэффициент ![]() возрастает (правда незначительно):
возрастает (правда незначительно):

Слагаемое ![]() представляет собой
перекрестную связь по углу
представляет собой
перекрестную связь по углу ![]() , которая возникает при неидентичности
зазоров подвесов. Оценим ее вклад коэффициентом
, которая возникает при неидентичности
зазоров подвесов. Оценим ее вклад коэффициентом 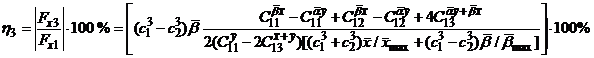
При ![]() коэффициент
коэффициент ![]() , т.е. является довольно
незначительной величиной.
, т.е. является довольно
незначительной величиной.
Составляющие ![]() и
и ![]() характеризуют собой нелинейности,
нелинейные перекрестные связи и перекрестные связи через потенциал ротора. При
малых отклонениях ротора из центра подвеса их величина не превышает десятых
долей процента.
характеризуют собой нелинейности,
нелинейные перекрестные связи и перекрестные связи через потенциал ротора. При
малых отклонениях ротора из центра подвеса их величина не превышает десятых
долей процента.
Учитывая численные оценки, можно утверждать, что при работе подвеса в линейной зоне при смещениях оси ротора не более 10% от зазора, можно пользоваться линеаризованными силовыми характеристиками, которые представим в виде
![]() (15)
(15)
В выражении
(15) ![]() при
одинаковых зазорах опор (
при
одинаковых зазорах опор (![]() ).
).
Перейдем теперь
к вычислению моментной характеристики ![]() . Также как и силовая характеристика
. Также как и силовая характеристика ![]() , она содержит пять
характерных составляющих:
, она содержит пять
характерных составляющих:

(16)
Стабилизирующую составляющую в статическом режиме с учетом (12) запишем в виде
![]()
она содержит перекрестную связь по ![]() , исчезающую при
, исчезающую при ![]() . Соотношения между
отдельными составляющими в (16) представляют собой величины того же порядка,
что и в (10), поэтому правомерно применение линеаризованной моментной характеристики
. Соотношения между
отдельными составляющими в (16) представляют собой величины того же порядка,
что и в (10), поэтому правомерно применение линеаризованной моментной характеристики
![]() (17)
(17)
В выражении
(17) перекрестная связь по ![]() исчезает при одинаковых зазорах опор.
исчезает при одинаковых зазорах опор.
Рассмотрим
теперь случай больших смещений ротора. Составляющие перемещения по осям x и y,
рис. 2, выраженные через абсолютное значение смещения d
и направление смещения ![]() можно
записать как
можно
записать как
![]() .
.
Угол рассогласования между вектором силы и направлением смещения будет равен

Очевидно, что
полезная составляющая силы противоположна направлению смещения. Действительно,
для возвращения ротора в центр подвеса необходимо, чтобы сила и смещение имели
разные знаки. Назовем полезную составляющую восстанавливающей силой, и будем
вычислять ее как ![]() .
Сила будет восстанавливающей в том диапазоне смещений, где
.
Сила будет восстанавливающей в том диапазоне смещений, где ![]() .
.
Проекции сил ![]() и
и ![]() будем рассчитывать по обобщенным
выражениям (6). Силовые характеристики цилиндрического подвеса в функции нормированного
смещения
будем рассчитывать по обобщенным
выражениям (6). Силовые характеристики цилиндрического подвеса в функции нормированного
смещения ![]() приведены
на рис. 3. Коэффициенты усиления по осям x и y выбирались
так, чтобы линейная зона подвеса была в пределах 10% от зазора h, опорное напряжение на электродах
приведены
на рис. 3. Коэффициенты усиления по осям x и y выбирались
так, чтобы линейная зона подвеса была в пределах 10% от зазора h, опорное напряжение на электродах ![]() . Анализ характеристик показывает
равножесткость при смещениях в любом направлении. Назовем диапазоном действия
восстанавливающей силы предельное смещение ротора, при котором сила и
перемещение имеют противоположные знаки. Для рассматриваемого случая диапазон
действия восстанавливающей силы
. Анализ характеристик показывает
равножесткость при смещениях в любом направлении. Назовем диапазоном действия
восстанавливающей силы предельное смещение ротора, при котором сила и
перемещение имеют противоположные знаки. Для рассматриваемого случая диапазон
действия восстанавливающей силы ![]() .
.

Рис. 3. Силовые характеристики цилиндрического подвеса
Рассмотрим,
каким образом величина линейной зоны подвеса влияет на вид силовой
характеристики. На рис. 4 приведены силовые характеристики при смещении в плоскости
![]() с линейными
зонами от 4 до 10% от зазора. Максимальная сила при уменьшении линейной зоны
растет, однако диапазон восстанавливающей силы не меняется.
с линейными
зонами от 4 до 10% от зазора. Максимальная сила при уменьшении линейной зоны
растет, однако диапазон восстанавливающей силы не меняется.
На рис. 5,
показано изменение силовых характеристик для трех значений зазора, при
сохранении одного и того же значения опорного напряжения на электродах. Также
наблюдается изменение максимальной силы при сохранении диапазона восстанавливающей
силы (все характеристики пересекаются в одной точке при ![]() ).
).
Полученные
результаты позволяют надлежащим образом выбрать размер упоров ![]() .
.

Рис. 4. Влияние размера линейной зоны на силовые характеристики подвеса

Рис. 5. Влияние зазора электрод-ротор на силовые характеристики подвеса
В реальных
образцах приборов с цилиндрическим подвесом смещение оси ограничено упорами.
Общий ход оси в упорах ![]() не
превышает
не
превышает ![]() . При
столь малой величине
. При
столь малой величине ![]() диапазон
действия восстанавливающей силы для цилиндрического подвеса менее существенен,
чем для сферического.
диапазон
действия восстанавливающей силы для цилиндрического подвеса менее существенен,
чем для сферического.
При наличии
упоров, более информативными, на наш взгляд являются характеристики,
построенные только в диапазоне смещений от нуля до ![]() (максимальное смещение оси). Обычно
подвесы проектируют для работы при больших жесткостях, линейная зона подвеса
при этом много меньше
(максимальное смещение оси). Обычно
подвесы проектируют для работы при больших жесткостях, линейная зона подвеса
при этом много меньше ![]() .
На рис. 6 приведены силовые характеристики для подвеса с линейной зоной
.
На рис. 6 приведены силовые характеристики для подвеса с линейной зоной ![]() , что при зазоре
, что при зазоре ![]() соответствует предельному
смещению в 0.2 мкм. Характеристики построены в функции нормированного смещения
соответствует предельному
смещению в 0.2 мкм. Характеристики построены в функции нормированного смещения ![]() .
.

Рис. 6. Силовые характеристики при смещениях, ограниченных упорами
Рассмотрим теперь,
как влияет угловое смещение оси на силовые характеристики подвеса. Как было
показано ранее, при идентичных опорах в выражении (15) ![]() и угловая жесткость силовой
характеристики
и угловая жесткость силовой
характеристики ![]() .
Однако это справедливо до тех пор, пока суммарное линейное x
и угловое
.
Однако это справедливо до тех пор, пока суммарное линейное x
и угловое ![]() смещение
(напомним, что напряжение датчика перемещения зависит от их линейной
комбинации) не выведет подвес из линейной зоны. Начиная с этого момента, при
росте линейного смещения или угла стабилизирующая составляющая силовой
характеристики не изменяется, а дестабилизирующая составляющая растет. При
наличии упоров максимальное линейное смещение
смещение
(напомним, что напряжение датчика перемещения зависит от их линейной
комбинации) не выведет подвес из линейной зоны. Начиная с этого момента, при
росте линейного смещения или угла стабилизирующая составляющая силовой
характеристики не изменяется, а дестабилизирующая составляющая растет. При
наличии упоров максимальное линейное смещение ![]() , а максимальное угловое смещение
, а максимальное угловое смещение ![]() . На рис. 7 показано, что
пока угловое смещение не выходит за пределы некоторой величины (порядка
. На рис. 7 показано, что
пока угловое смещение не выходит за пределы некоторой величины (порядка ![]() ), подвес сохраняет свои
восстанавливающие способности во всем диапазоне возможных смещений (от нуля до
), подвес сохраняет свои
восстанавливающие способности во всем диапазоне возможных смещений (от нуля до ![]() ).
).

Рис. 7. Влияние малых угловых смещений на силовые характеристики подвеса
Однако
дальнейший рост ![]() ,
рис.8, вызывает появление в зоне малых линейных смещений участка
характеристики, где
,
рис.8, вызывает появление в зоне малых линейных смещений участка
характеристики, где ![]() .
На этом участке подвес теряет свои восстанавливающие свойства.
.
На этом участке подвес теряет свои восстанавливающие свойства.

Рис. 8. Влияние больших угловых смещений на силовые характеристики подвеса
Как можно
объяснить это явление? При преобладании углового смещения и выходе подвеса из
линейной зоны на парах электродов Э3, Э4 и Э7, Э8 (в данном случае мы рассматриваем
смещения в плоскости ![]() )
устанавливаются предельные значения потенциалов
)
устанавливаются предельные значения потенциалов ![]() и 0. Их фазировка становится такой, что
стабилизирующие составляющие сил левой и правой опор компенсируют друг друга.
Дестабилизирующие составляющие зависят только от величины линейного смещения,
они складываются. Это и приводит к появлению участка, где
и 0. Их фазировка становится такой, что
стабилизирующие составляющие сил левой и правой опор компенсируют друг друга.
Дестабилизирующие составляющие зависят только от величины линейного смещения,
они складываются. Это и приводит к появлению участка, где ![]() .
.
То же
происходит и с моментными характеристиками, рис. 9. При росте линейного
смещения x, начиная с некоторого его значения на
моментных характеристиках появляется участок ![]() . Возникает вопрос, существуют ли такие
комбинации линейных и угловых смещений при которых подвес полностью теряет свои
восстанавливающие свойства (
. Возникает вопрос, существуют ли такие
комбинации линейных и угловых смещений при которых подвес полностью теряет свои
восстанавливающие свойства (![]() ). Моделирование показывает, что не существуют.
На рис. 10 вся область возможных линейных и угловых смещений разбита на три
подобласти.
). Моделирование показывает, что не существуют.
На рис. 10 вся область возможных линейных и угловых смещений разбита на три
подобласти.

Рис. 9. Влияние больших угловых смещений на восстанавливающий момент

Рис. 10. Области устойчивости силовых и моментных характеристик
1. ![]() (подобласть 1). Здесь
суммарное линейное и угловое смещение не выводят подвес (или хотя бы одну его
опору) из линейной зоны и восстанавливающие способности полностью сохраняются.
(подобласть 1). Здесь
суммарное линейное и угловое смещение не выводят подвес (или хотя бы одну его
опору) из линейной зоны и восстанавливающие способности полностью сохраняются.
2. ![]() (подобласть 2). Подвес
обладает восстанавливающими свойствами по угловому смещению, но не обладает по
линейному смещению.
(подобласть 2). Подвес
обладает восстанавливающими свойствами по угловому смещению, но не обладает по
линейному смещению.
3. ![]() (подобласть 3). Есть
восстанавливающие свойства по силе, и нет по моменту.
(подобласть 3). Есть
восстанавливающие свойства по силе, и нет по моменту.
Значит ли это, что при начальном центрировании из подобластей 2 и 3 подвес будет неустойчивым? Для того чтобы установить, теряет ли при этом подвес устойчивость, было проведено моделирование процессов всплытия ротора из разных начальных точек.
Вначале
осуществлялось всплытие ротора из зоны 1, рис. 10, где и по силе, и по моменту
подвес обладает восстанавливающей способностью ![]() . Переходные процессы по линейному и угловым
смещениям оси ротора показаны на рис. 11 а, б.
. Переходные процессы по линейному и угловым
смещениям оси ротора показаны на рис. 11 а, б.

Рис. 11. Переходные процессы всплытия ротора из зон 1, 2, 3 (рис. 10)
В течение всего времени переходного процесса происходит уменьшение как линейной, так и угловой координаты до полного центрирования.
При всплытии из
зоны 2 ![]() на
начальной стадии переходного процесса по линейной координате, рис. 11 в,
имеется участок медленного роста линейного смещения. Угловое же смещение, рис.
11 г, уменьшается, причем значительно быстрее, чем растет линейное смещение.
Это приводит к тому, что рабочая точка переходит в подобласть 1 и подвес снова приобретает
восстанавливающие свойства.
на
начальной стадии переходного процесса по линейной координате, рис. 11 в,
имеется участок медленного роста линейного смещения. Угловое же смещение, рис.
11 г, уменьшается, причем значительно быстрее, чем растет линейное смещение.
Это приводит к тому, что рабочая точка переходит в подобласть 1 и подвес снова приобретает
восстанавливающие свойства.
При всплытии из
зоны 3 ![]() на
начальной стадии переходного процесса наблюдается рост угловой координаты,
рис. 11 е, с последующим восстановлением центрирующих свойств.
на
начальной стадии переходного процесса наблюдается рост угловой координаты,
рис. 11 е, с последующим восстановлением центрирующих свойств.
Таким образом, моделирование подтверждает, что подвес сохраняет восстанавливающие свойства при всплытии из областей 2 и 3.
В последнее время начали широко применяться подвесы, в которых вместо аналоговых систем регулирования используются импульсные или дискретные системы. Рассмотрим импульсные законы управления электростатическими подвесами, потенциалы, на электродах которых регулируются по принципу ШИМ (широтно-импульсной модуляции). В работе [2] показано, что минимальный наведенный потенциал ротора обеспечивается при законе управления
 (18)
(18)
Приращение
длительности ![]() импульсов
ШИМ на паре диаметрально противоположных электродов пропорционально напряжению
датчика перемещений и формируется в виде
импульсов
ШИМ на паре диаметрально противоположных электродов пропорционально напряжению
датчика перемещений и формируется в виде
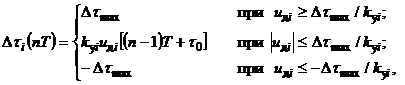 (19)
(19)
где ![]() - фиксированный промежуток времени,
обеспечивающий оптимальное функционирование импульсного датчика перемещения [2].
- фиксированный промежуток времени,
обеспечивающий оптимальное функционирование импульсного датчика перемещения [2].
Величина ![]() не должна достигать
половины периода квантования или превышать ее, так как в противном случае
импульсы на электродах вырождаются в постоянный уровень, что нарушает работу
датчиков перемещения.
не должна достигать
половины периода квантования или превышать ее, так как в противном случае
импульсы на электродах вырождаются в постоянный уровень, что нарушает работу
датчиков перемещения.
Смысл
коэффициентов ![]() тот
же, что и в подвесах на постоянном токе. Рассмотрим вариант распределения
уставок на электродах подвеса [2], наиболее полно минимизирующий наведенный
потенциал ротора
тот
же, что и в подвесах на постоянном токе. Рассмотрим вариант распределения
уставок на электродах подвеса [2], наиболее полно минимизирующий наведенный
потенциал ротора
![]() (20)
(20)
При смещении ротора из центра подвеса приращения длительностей импульсов на электродах в соответствии с (11), (18), (19) и (20) составляют
![]()
Временные диаграммы потенциалов на радиальных электродах при произвольном смещении оси ротора приведены на рис. 12, а на осевых – на рис. 13.
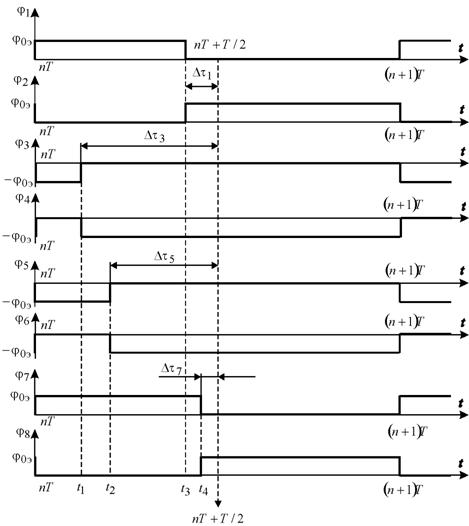
Рис. 12. Временные диаграммы импульсов на радиальных электродах

Рис. 13. Временные диаграммы импульсов на осевых электродах
Разобьем период регулирования на ряд однородных участков и вычислим значения сил и моментов для каждого из них. Далее, проводя осреднение на периоде, окончательно получим
 (21)
(21)
И, наконец,
приведем, рис.14, осредненные силовые характеристики импульсного
цилиндрического подвеса при произвольных (в том числе и больших) смещениях.
Здесь прослеживается та же, что и для сферических подвесов, тенденция уменьшения
области действия восстанавливающей силы (![]() ) по сравнению с подвесами на постоянном
токе.
) по сравнению с подвесами на постоянном
токе.
Анализ силовых и моментных характеристик, проведенных в данной главе, показывает, что при выполнении надлежащих мер по минимизации потенциала ротора и при малых смещениях ротора из центра подвеса дестабилизирующая составляющая в силовых характеристиках на порядок меньше стабилизирующей составляющей, вклад нелинейных членов также мал. В этих условиях возможна линеаризация силовых характеристик, что значительно упрощает исследование устойчивости “в малом” и качества подвесов.
При больших смещениях и на этапе начального всплытия ротора использование линеаризованных силовых характеристик приводит к большим погрешностям. В этом случае необходимо исследовать полную нелинейную модель подвеса с учетом перекрестных связей и наведенного потенциала ротора.

Рис. 14. Силовые характеристики импульсного подвеса
СПИСОК ЛИТЕРАТУРЫ
1. Мартыненко Ю. Г. Движение твердого тела в электрических и магнитных полях. М.: Наука, 1988.
2. С. А. Васюков, Г. Ф. Дробышев. Алгоритмы управления потенциалами на электродах электростатического подвеса//Вестник МГТУ им. Н. Э. Баумана. Сер. Приборостроение.-2007.-╧2.-С. 69-81.
3. С. А. Васюков, Г. Ф. Дробышев. Математическая модель цилиндрического электростатического подвеса как системы заряженных проводников //Вестник МГТУ им. Н. Э. Баумана. Сер. Фундаментальные науки.-2007.-╧ 1.-С.72-87 .
4. Тамм И. Е. Основы теории электричества. М.: Наука, 1966.
Публикации с ключевыми словами: электростатический подвес, силовая характеристика, цилиндрический ротор
Публикации со словами: электростатический подвес, силовая характеристика, цилиндрический ротор
Смотри также:
- О влиянии законов управления потенциалами на силовые характеристики сферического электростатического подвеса
- Об одном способе улучшения статической и динамической равножесткости в трехосном электростатическом подвесе
- Об одном способе повышения стабильности центрирования ротора электростатического подвеса
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



