научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#1 январь 2008
Харламов В.В.
Научный руководитель: к.ф.-м.н., доцент Храпов П.В.
Кафедра ФН1, МГТУ им. Н.Э. Баумана, Москва, Россия.
Согласно современным историческим сведениям, сплайны (от англ. spline – длинная узкая полоса дерева или металла; рейка) использовались судостроителями еще в XVI веке. Перед ними стояла следующая задача: через опорные точки, расположение которых известно, требуется провести непрерывную гладкую кривую. Задача решалась путем закрепления в этих точках гибкой деревянной рейки, которая, изгибаясь, принимала требуемую форму. Для разрешения проблем подобного рода методами прикладной математики применяется интерполяция [2].
Определение. Интерполяцией называется приближенное или точное нахождение значений какой-либо величины по известным отдельным значениям этой величины или значениям других величин, связанных с данной.
Форма физического сплайна (отклонение y) определяется уравнением Эйлера [1] для момента изгиба M(x) вдоль рейки:
![]()
где E – модуль Юнга, зависящий от свойств материала рейки, I – момент инерции, определяемый формой кривой, R(x) – радиус кривизны.
Для малых отклонений (y’ << 1) справедливо приближенное равенство
![]()
Уравнение Эйлера принимает вид
![]()
Момент изгиба между точками закрепления изменяется линейно. Подставляя M(x) = Ax+B в уравнение Эйлера, получаем:
![]()
и после двойного интегрирования
![]()
Таким образом, форма сплайна задается кубическим полиномом.
Определение. Сплайном порядка m называется функция, которая является многочленом степени m на каждом из частичных интервалов [xi-1, xi] (i = 1, 2, …, n), принимает заданные значения yi в узлах xi (i = 0, 1, 2, …, n) и имеет непрерывные производные до (m – 1)-го порядка включительно.
Кубический сплайн имеет в узловых точках непрерывные производные до второго порядка включительно. По аналогии с физическими сплайнами обычно используется серия кубических сплайновых сегментов, причем каждый сегмент проходит через две точки.
Цель данной работы – разработка программы, строящей стереоизображение замкнутой сплайновой кривой, проходящей через заданные узловые точки с заданными радиус-векторами P0,…, Pn (см. рис. 1).
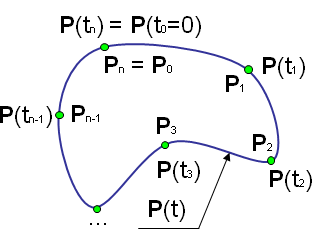
Рис. 1
Векторное параметрическое уравнение сплайновой кривой на i-м частичном интервале имеет вид
P(t) = Ai + Bi(t - ti-1) + Ci(t - ti-1)2 + Di(t - ti-1)3, (1a)
где ti-1 ≤ t ≤ ti (i = 1, …, n), n – число сплайновых сегментов
Значения параметра в узловых точках задаются следующим образом: t0 = 0, а разность ti - ti-1 (i = 1, …, n) принимается равной расстоянию между соответствующими узловыми точками.
Коэффициенты многочлена на каждом интервале определяют из условий в узлах:
- условие прохождения кривой через узловые точки:
P(ti-1) = Pi-1 = Ai; (1b)
- условия непрерывности первой и второй производных в узловых точках:
P’(ti - 0) = P’(ti + 0); (1c)
P”(ti - 0) = P”(ti + 0); (1d)
- циклические концевые условия (требование замкнутости кривой):
P’(t0) = P’(tn); (1e)
P”(t0) = P”(tn). (1f)
Из (1a):
P(ti) = Ai + Bihi + Cihi2 + Dihi3, (2)
где hi = ti - ti-1, i = 1, …, n;
P’(t) = Bi + 2Ci(t - ti-1) + 3Di(t - ti-1)2; (3)
P”(t) = 2Ci + 6Di(t - ti-1). (4)
Из (3) и (1с):
P’(ti - 0) = Bi + 2Cihi + 3Dihi2 = P’(ti + 0) = Bi+1. (5)
Из (4) и (1d):
P”(ti - 0) = 2Ci + 6Dihi = P”(ti + 0) = 2Ci+1. (6)
Из (6): Di = (Ci+1 – Ci)/(3hi). (7)
Из (1b), (2) и (7):
Bi = (Pi – Pi-1)/hi – Cihi – Dihi2 =
= (Pi – Pi-1)/hi – Cihi - hi2(Ci+1 – Ci)/(3hi) =
= (Pi – Pi-1)/hi – hi(2Ci + Ci+1)/3. (8)
Подставим (7) и (8) в (5):
(Pi – Pi-1)/hi – hi(2Ci + Ci+1)/3 + 2Cih + 3hi2(Ci+1 – Ci)/(3hi) =
= (Pi+1 – Pi)/hi+1 – hi+1(2Ci+1 + Ci+2)/3; =>
=> hiCi/3 + (2hi/3 + 2hi+1/3)Ci+1 + hi+1Ci+2/3 = (Pi+1 – Pi)/hi+1 - (Pi – Pi-1)/hi. (*)
Из (1e) и (3):
B1 = Bn + 2Cnhn + 3Dnhn2. (9)
Подставим (7) и (8) в (9):
(P1 – P0)/h1 – h1(2C1 + C2)/3 = (Pn - Pn-1)/hn –
– hn(2Cn + Cn+1)/3 + 2Cnhn + 3hn2(Cn+1 – Cn)/(3hn); =>
=> 2h1C1 + h1C2 + hnCn + 2hnCn+1 = 3(P1 - P0)/h1 – 3(Pn - Pn-1)/hn. (**)
Из (1f) и (4):
2C1 = 2Cn + 6Dnhn. (10)
Подставим (7) в (10):
2C1 = 2Cn + 6hn(Cn+1 – Cn)/(3hn), => C1 – Cn+1 = 0. (***)
Уравнения (*), (**) и (***) образуют систему линейных алгебраических уравнений (СЛАУ) с n + 1 уравнениями и неизвестными. Из нее находятся коэффициенты Ci, затем коэффициенты Ai, Bi, Di находятся из уравнений (1b), (8), (7). Полученная СЛАУ не является системой специального вида, и к ней неприменимы специальные методы решения. В разработанной демонстрационной программе эта система уравнений решается методом Гаусса с выбором главного элемента [3].
По уравнению (1a) после нахождения его коэффициентов можно для любого допустимого значения параметра t найти координаты соответствующей точки сплайна. Изображение сплайновой кривой строится по точкам методом линейной аппроксимации.
Следующий шаг – создание стереоизображения. Во многих приложениях важно увеличение восприятия трехмерной глубины сцены. Бинокулярное зрение дает очень сильное восприятие глубины, потому что система глаз-мозг смешивает в одно два различных изображения, видимых каждым глазом. Стереография пытается создать изображение с характеристиками, аналогичными настоящему бинокулярному зрению.
Один из методов создания стереоизображений называется цветовым анаглифом [1]. Суть его в том, что создаются двумя разными цветами два изображения – одно для левого и другое для правого глаза. При просмотре через соответствующие светофильтры левый глаз видит только левое изображение, а правый – только правое. Система глаз-мозг объединяет оба плоских изображений в одно трехмерное.
На рис. 2 показана схема хода лучей при просмотре стереоизображения, а также приведены расчетные схемы и зависимости, необходимые для вычисления координат точек стереоизображения.
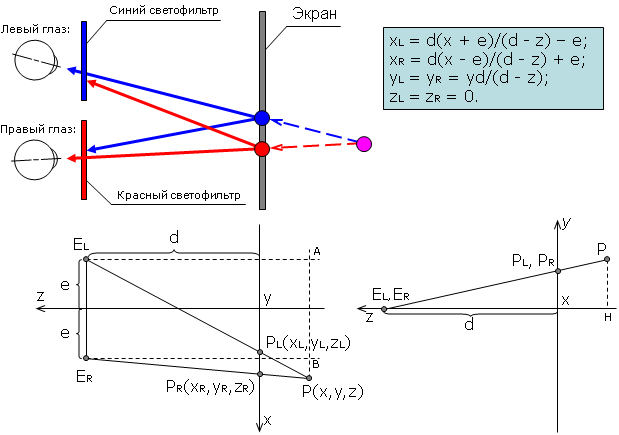
Рис. 2
Здесь P – точка видимого трехмерного изображения, PR и PL – точки на экране, предназначенные для наблюдения правым и левым глазами соответственно. Приведенные зависимости позволяют для каждой найденной точки P сплайновой кривой определить экранные координаты соответствующих ей точек PR и PL стереоизображения, которое, так же как и сплайн, строится методом линейной аппроксимации.
Демонстрационная программа написана на языке C++ с использованием графической библиотеки OpenGL и предназначена для функционирования в операционной системе MS Windows XP [3]. Программа позволяет интерактивно задавать узловые точки сплайна, а также осуществлять вращение кривой для удобства просмотра.
Замечание: для наблюдения стереоизображения необходимы анаглифические очки с красным и синим светофильтрами.
Пример работы программы приведен на рис. 3.

Рис. 3
Кубические сплайны являются мощным и удобным средством получения гладких интерполяционных кривых. Кусочные сплайны из многочленов невысокого порядка не требуют больших вычислительных затрат и не вызывают численных отклонений, свойственных многочленам высокого порядка. Кубический сплайн удобен еще и тем, что это кривая наименьшего порядка, допускающая точки перегиба. К недостаткам кубических сплайнов можно отнести необходимость учитывать влияние направления и величины касательных векторов, а также невозможность локальной коррекции сплайновых кривых [1].
Литература
1. Роджерс Д., Адамс Дж. Математические основы машинной графики: Пер. с англ. – М.: Мир, 2001.
2. Самарский А. А., Гулин А. В. Численные методы: учебное пособие для вузов. – М.: Наука. Гл. ред. физ-мат. лит., 1989.
3. Черносвитов. А. Visual C++ 7: учебный курс. – СПб.: Питер, 2001.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



