научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#3 март 2008
УДК[681.78.01: 681.3] (075.8)
Ю.А.Лушин
К наиболее распространенным методам измерения оптических передаточных функций (ОПФ) можно отнести:
-метод непосредственного сканирования;
-метод электронного Фурье анализатора;
- метод оптического Фурье-анализатора.
Все указанные методы предполагают необходимость заполнения всего входного зрачка контролируемой системы коллимированным потоком излучения. При этом аберрационное качество коллимирующей оптической системы должно быть не хуже качества контролируемой [10], что является сложной технической и экономической проблемой.
Ниже рассмотрен зонный способ измерения некогерентных оптических передаточных функций (ОПФ) приемных систем оптико-электронных приборов (ОЭП) с крупногабаритной оптикой без использования уникальных крупногабаритных коллимирующих оптических систем.
Как известно [1,2,6,7,11], некогерентная оптическая передаточная функция оптической системы (ОС) может быть представлена как функция автоковариации входного зрачка:
![]() H(νх ,νу)
= Р(λƒ'νх
, λƒ'νу)
* Р*(λƒ'νх
, λƒ'νу)
(1),
H(νх ,νу)
= Р(λƒ'νх
, λƒ'νу)
* Р*(λƒ'νх
, λƒ'νу)
(1),
где H(νх ,νу) – ненормированная ОПФ ОС;
Р(λƒ'νх , λƒ'νу) – функция зрачка ОС;
Р*(λƒ'νх , λƒ'νу) – комплексно сопряженная функция зрачка ОС;
* - символическое обозначение операции корреляции;
λ – длина волны оптического излучения;
ƒ' – заднее фокусное расстояние ОС;
νх , νу – пространственные частоты вдоль осей ОХ и ОУ соответственно.
Функция зрачка представляет собой комплексную функцию пропускания, которая описывается выражением [6,7,10]:
![]() Р(ξ,η)=
[τ(ξ,η)]½ exp[jкW(ξ,η)]
Р(ξ,η)=
[τ(ξ,η)]½ exp[jкW(ξ,η)] ![]() (2),
(2),
где τ(ξ,η) – коэффициент пропускания входного зрачка по интенсивности;
W(ξ,η) – волновая монохроматическая аберрация оптической системы- определяет степень отклонения реальной части волнового фронта от сферы сравнения, измеряемой вдоль радиуса идеальной.монохроматической волны;
к – волновое число.
Для упрощения дальнейших выкладок будем рассматривать одномерную некогерентную ОПФ.
Пусть имеется произвольная некогерентная ОС, входной зрачок которой изображен на рисунке 1. Впишем входной зрачок в прямоугольник со сторонами Dξ и Dη по осям Оξ и Оη соответственно. Разделим входной зрачок на N равных частей вдоль осей Оξ и Оη. Пусть входной зрачок описывается функцией Р(ξ,η). В дискретных координатах функцию зрачка можно рассматривать как сумму зональных зрачковых функций:
Р(ξ,η)
= ![]() Рiℓ(ξ,η)=
Рiℓ(ξ,η)= 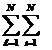 [τЁℓ(ξ,η)]½ exp[jкWЁℓ(ξ,η)] (3),
[τЁℓ(ξ,η)]½ exp[jкWЁℓ(ξ,η)] (3),
где Рiℓ (ξ , η) – функция элементарной области входного зрачка оптической системы ;
i ,ℓ -дискретные координаты элементарной области входного зрачка
оптической системы ;
i = 1,2,3, ... N;
ℓ = 1,2,3, ... N;
ξ = λf'νх , η = λf'νу;
τЁℓ(ξ,η) - коэффициент пропускания по интенсивности элементарной области входного зрачка;
WЁℓ(ξ,η) - волновая аберрация элементарной части волнового фронта.
Подставив (3) в (1), получим выражение для одномерной ОПФ, представляющей собой функцию автоковариации входного зрачка по координате Оνх :
H(νх ,0) = ![]() [
[![]() Рiℓ(ξ)*
Рiℓ(ξ)*![]() Р*iℓ(ξ)] =
Р*iℓ(ξ)] = ![]() [
[![]() Рi(ξ)*
Рi(ξ)*![]() Р*i(ξ)]ℓ (4).
Р*i(ξ)]ℓ (4).
Раскроем выражение (4), опуская для упрощения записи аргументы функции зрачка :
H(νх ,0) = ![]() [(Р1+Р2+…+РN) * (Р1*+Р2*+…
+РN*)]ℓ =
[(Р1+Р2+…+РN) * (Р1*+Р2*+…
+РN*)]ℓ =
= ![]() [
(Р1*Р1*+Р2*Р2*+…+
РN* РN*)+
[
(Р1*Р1*+Р2*Р2*+…+
РN* РN*)+
+Р1*Р2*+Р1*Р3*+… +Р1*РN*+
+Р2*Р1*+Р2*Р3*+Р2< /sub>*Р4*…+Р2*РN*+
+………………………….+
+РN*Р1*+РN*Р2*+…+РN*РN-1*]ℓ (5).
Преобразуем выражение (5) в такой вид, когда ОПФ может быть представлена в виде совокупности функций автоковариации. Для этого рассмотрим выражение :
(Рi+Рк)*(Рi+Рк) *=Рi*Рi*+Рк*Рк*+Р i*Рк*+Рк*Рi* (6).
Выражение (6) в символичной форме определяет ненормированную ОПФ системы, когда входной зрачок представляет собой совокупность двух элементарных пространственных областей. Выражение (6) перепишем в виде :
(Рi+Рк)*(Рi+Рк)* – (Рi*Рi*+ Рк*Рк*) =Рi*Рк*+Рк*Рi* (7).
Представим члены вида Рi*Рк*+Рк*Рi* в выражении (5) в виде левой части выражения (7):
H(νх ,0) = ![]() [
[![]() Рi*Рi*-(N-1)
Рi*Рi*-(N-1)![]() Рi*Рi+
Рi*Рi+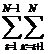 (Рi+Рк)*(Рi+Рк)*]ℓ
=
(Рi+Рк)*(Рi+Рк)*]ℓ
=
=![]() [
[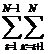 (Рi+Рк)*(Рi+Рк)*-
(N-2)
(Рi+Рк)*(Рi+Рк)*-
(N-2)![]() Рi*Рi*]ℓ =
Рi*Рi*]ℓ =
=![]() [
[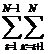 Hiĸ(νх ,0) - (N-2)
Hiĸ(νх ,0) - (N-2)![]() Hii(νх ,0)]ℓ (8),
Hii(νх ,0)]ℓ (8),
где Hiĸ(νх ,0)= (Рi+Рк)*(Рi+Рк)*- одномерная ОПФ системы, когда её входной зрачок представляет собой совокупность двух элементарных зон, являющимися элементами одной строки.
Hii(νх ,0) = Рi*Рi*-одномерная ОПФ системы, когда её входной зрачок представляет собой одну элементарную область зрачка контролируемой ОС.
Нормированная ОПФ системы определяется выражением :
![]()
![]()
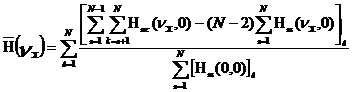 (9).
(9).
Полученное выражение описывает ОПФ аберрационной ОС в виде совокупности зонных ОПФ, являющимися функциями автокорреляции элементарных частей входного зрачка ОС.
На основании (8), способ измерения
ОПФ крупногабаритных ОС без использования уникальных крупногабаритных
коллимирующих устройств заключается в следующем : входной зрачок аберрационной
ОС заполняется последовательно сначала одним, а затем двумя одинаковыми не
перекрывающимися пучками коллимированного модулированного излучения, несущими
информацию о тест объекте. Пучки перемещаются дискретно коллениарно друг другу
вдоль оси пространственных частот измеряемой ОПФ, а также совместно друг с
другом перпендикулярно этой оси в определенные фиксированные положения с шагом,
равным размеру выходного зрачка ![]() коллимированного излучения. По
измеренным зонным ОПФ по формуле (9)рассчитывают ОПФ контролируемой оптической
системы.
коллимированного излучения. По
измеренным зонным ОПФ по формуле (9)рассчитывают ОПФ контролируемой оптической
системы.
Зонный способ измерения ОПФ поясняется схемой, приведенной на рисунке 1.
Число необходимых положений коллимирующих пучков (число циклов измерения одномерной ОПФ) определяется по формуле :
![]() (10)
(10)
Так для N=3,число циклов измерения составит n=18;
для N=4, число циклов измерения составит n=40;
для N=5, число циклов измерения составит n=75;
для N=6, число циклов измерения составит n=126.
Как следует из приведенных расчетов, для уменьшения трудоемкости измерения ОПФ крупногабаритных оптических систем,число N должно выбираться в пределах N=3-6.
Рассмотрим простейший пример вычисления ОПФ зонным способом. Пусть имеется дифракционно ограниченная ОС, входной зрачок которой представляет квадрат со стороной А. Коэффициент пропускания зрачка по интенсивности постоянен в пределах зрачка и равен 1. Входной зрачок представлен на рисунке 2.
Представим входной зрачок в виде совокупности 9 зон, разделив его по осям ОХ и ОУ на три равные части. Размер каждой зоны по осям ОХ и ОУ составит а=А/3.
Для определения одномерной ОПФ в данном случае необходимо вычислить ОПФ каждой строки разбиения зрачка, просуммировав полученные результаты в соответствии с выражением (9) по оси ОУ.
Как известно[6,7], нормированная одномерная ОПФ некогерентной дифракционно ограниченной ОС с прямоугольным входным зрачком определяется выражением :
![]()
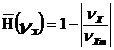 (11),
(11),
где νхm=![]()
![]() - максимальная пространственная частота ОС.
- максимальная пространственная частота ОС.
Для рассматриваемого примера выражение (9) примет вид:
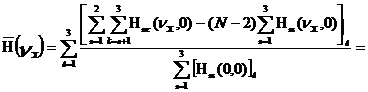

![]()
![]()
![]()
![]()
![]()
![]()
![]() (12).
(12).
Из выражения (12) следует, что для вычисления одномерной ОПФ ОС необходимо: :
1. последовательно определить функции автоковариации входного зрачка, сначала представляющего собой совокупность двух элементарных зон, а затем каждой элементарной зоны зрачка в отдельности;
2. просуммировать по пространственным частотам функции автоковариации двойных зон и вычесть из полученного выражения сумму функций автоковариации одинарных зон;
3. пронормировать полученное выражение на сумму значений функций автоковариации одинарных зон на нулевой пространственной частоте.
Нетрудно показать,что функции автоковариации совокупности двух зон (зонные ОПФ) определяются выражениями:
![]() H12(νх ,0)ℓ=(Р1+Р2)ℓ*(Р1+Р2)ℓ*=
H12(νх ,0)ℓ=(Р1+Р2)ℓ*(Р1+Р2)ℓ*= 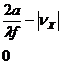
![]()
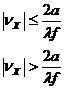
![]() H23(νх ,0)ℓ=(Р2+Р3)ℓ*(Р2+Р3)ℓ*=
H23(νх ,0)ℓ=(Р2+Р3)ℓ*(Р2+Р3)ℓ*= 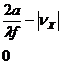
![]()
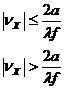
![]() H13(νх ,0)ℓ=(Р1+Р3)ℓ*(Р1+Р3)ℓ*=
H13(νх ,0)ℓ=(Р1+Р3)ℓ*(Р1+Р3)ℓ*= 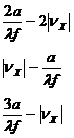
![]()
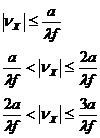
![]() H11(νх)= H22(νх)=
H11(νх) =
H11(νх)= H22(νх)=
H11(νх) = 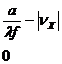
 (13).
(13).
Нормирующий член в выражении (12):
![]()
![]() [H11(0)+H22(0)+H11(0)] = 9
[H11(0)+H22(0)+H11(0)] = 9![]() (14).
(14).
В соответствии с выражением (12) с учетом (13) и (14) получим:
![]()
![]()
![]()
![]()

![]()
![]()

![]()
![]()
 (15),
(15),
где ![]() .
.
С учетом симметричности на рисунке 3 представлены правые части графиков зонных ОПФ. Таким образом, вычисленная зонным способом ОПФ оптической системы, как следует из выражений (15), полностью совпадает с известным исходным выражением (11), что подтверждает правильность полученного выражения (9), определяющего алгоритм вычисления ОПФ некогерентной оптической системы зонным способом.
Для оптической системы обладающей аберрациями, функция зрачка представляет собой комплексную функцию пропускания, которая описывается выражением (2). Оптическая передаточная функция в общем виде описывается выражением [2,8,10]:
![]()
![]() expjФ
expjФ![]() =
= ![]() [cosФ
[cosФ![]() + jsinФ
+ jsinФ![]() ]
]![]()
![]()
![]()
![]() (16),
(16),
где![]()
![]() - модуляционная передаточная функция
оптической системы,
- модуляционная передаточная функция
оптической системы,![]()
Ф![]() - функция передачи фазы.
- функция передачи фазы.![]()
С учетом выражения (16) выражение (9) примет вид:
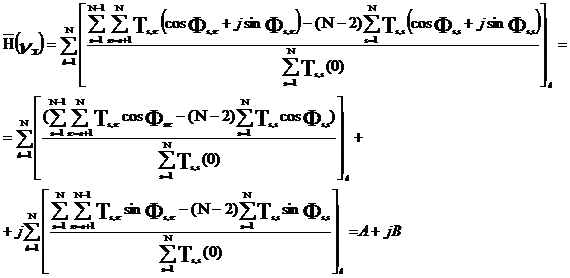
![]() (17),
(17),
В выражении (17):
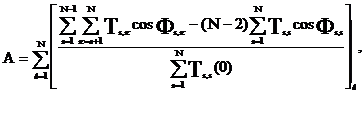
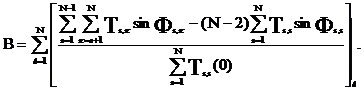
![]()
В выражении (17) для упрощения записи аргументы функций опущены.
![]() Модуляционная передаточная
функция и функция передачи фазы аберрационной оптической системы вычисляются по
известным формулам:
Модуляционная передаточная
функция и функция передачи фазы аберрационной оптической системы вычисляются по
известным формулам:
![]()
![]() (18),
(18),
![]()
![]() (19).
(19).
Выражения (17),(18),(19) определяют алгоритм вычисления ОПФ крупногабаритной оптической системы по измеренным зонным модуляционным передаточным функциям и функциям передачи фазы
-
Основными методическими погрешностями
измерения ОПФ являются несоосность коллимирующих устройств и отступление от
плоскостности выходящего волнового фронта (дефокусировка). Максимально
допустимая величина несоосности коллимирующих устройств была рассчитана из
условия допустимого снижения точности измерения ОПФ не более 10% на
пространственных частотах ![]() max,
max,
где -![]() - пространственная частота
некогерентной ОС;
- пространственная частота
некогерентной ОС;
-![]() max - максимальная пространственная
частота некогерентной ОС.
max - максимальная пространственная
частота некогерентной ОС.
Максимальная допустимая несоосность, определяемая как несоосность двух крайних коллимированных пучков излучения, определяется выражением:
![]()
![]()
![]() (20),
(20),
где ![]() - максимальная допустимая
несоосность коллимированных пучков в секундах;
- максимальная допустимая
несоосность коллимированных пучков в секундах;
![]() - длина волны в микрометрах;
- длина волны в микрометрах;
D –диаметр входного зрачка контролируемой ОС в метрах.
Так, например, для длины волны ![]() =10мкм и диаметра входного зрачка
контролируемой ОС –D=1,0 м, максимальная
допустимая несоосность коллимирующих устройств не должна превышать 2,6 угловых
секунды, что
=10мкм и диаметра входного зрачка
контролируемой ОС –D=1,0 м, максимальная
допустимая несоосность коллимирующих устройств не должна превышать 2,6 угловых
секунды, что
реально достижимо на практике.
Допустимая величина продольной дефокусировки тест-объекта относительно передней фокальной плоскости коллиматора определяется выражением:
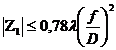 (21),
(21),
где Z1 - допустимая величина продольной дефокусировки тест-объекта относительно передней фокальной плоскости коллиматора в мм;
λ – длина волны в мкм;
f – переднее фокусное расстояние коллиматора в мм;
D – диаметр входного зрачка контролируемой ОС в мм.
Представленный в данной статье зонный способ измерения и вычисления оптических передаточных функций приемных систем оптико-электронных приборов (ОЭП) с крупногабаритной оптикой позволяет:
- объективно оценить качество приемных систем ОЭП на этапе выходных испытаний без использования уникальных крупногабаритных коллимирующих устройств,
- осуществлять юстировку приемных систем ОЭП,
- контролировать на одной установке без переналадки и изменения ее параметров широкий класс приемных систем ОЭП, существенно отличающихся размерами входных зрачков,
-значительно уменьшить стоимость контрольно-юстировочной аппаратуры за счет исключения из нее уникальных высококачественных крупногабаритных коллиматоров.
- СПИСОК ЛИТЕРАТУРЫ
1. Борн М., Вольф Э., Основы оптики, - М.: Наука, 1970, 422 с.
2. Гудмен Дж., Введение в Фурье оптику. – М.: Мир, 1970.
3. Криксунов Л.З. и др. Частотно-временные и пространственно-частотные характеристики модулирующих устройств. М.: Машиностроение, 1976, 132 с.
4. Левшин В.Л., Пространственная фильтрация в оптических системах пеленгации. М.: Советское радио, 1971, 200 с.
5. Марешаль А., Франсон М. Структура оптического изображения. – М.: Мир, 1964, 296 с.
6. Мосягин Г.М., Немтинов В.Б., Лебедев Е.Н. Теория оптико-электронных систем. М.: Машиностроение, 1990. 431 с.
7. Мосягин Г.М., Немтинов В.Б., Преобразование сигналов в оптико-электронных приборах систем управления летательными аппаратами. М.: Машиностроение, 1980. 175 с.
8. О'Нейл Э., Введение в статистическую оптику.. – М.: Мир, 1966, 254 с.
9. Папулис А., Теория систем и преобразований в оптике. М.: Мир, 1971, 496 с.
10.Шульман М.Я., Измерение передаточных функций оптических систем. Л.: Машиностроение. Ленингр. отд-ние, 1980, 208 с., ил.
11.Юу Ф.Т.С., Введение в теорию дифракции, обработку информации и голографию. М.: Сов. Радио, 1979, 304с.
Рисунок 1 Зонный способ измерения некогерентной оптической передаточной функции оптической системы
1 – входной зрачок контролируемой оптической системы;
2,3 – коллимирующие устройства;
4 – направляющая опора;
5 – анализирующее устройство.
Рисунок 2 Входной зрачок оптической системы
Рисунок 3 Зонные ОПФ
В рамках скалярной теории дифракции предложен и теоретически обоснован
зонный способ измерения оптических передаточных функций крупногабаритных оптических систем, позволяющий объективно оценить качество приемных систем оптико-электронных приборов на этапе выходных испытаний без использования уникальных крупногабаритных коллимирующих устройств.
Within the limits of the scalar diffraction theory it is offered and theoretically proved zone way of measurement of optical transfer functions of the large-sized optical systems, allowing objectively estimation quality of receiving systems of optical-electronic devices at a stage of target tests without use unique large-sized collimating equipment.
Юрий Андреевич Лушин родился в 1951 г., окончил МВТУ им. Н.Э. Баумана в 1974 г. Канд. тех. наук, доцент кафедры “Лазерные и оптико-электронные системы” МГТУ им. Н.Э. Баумана. Автор 30 научных публикаций в области проектирования и производства оптико-электронных приборов управления.
Yury Andreevich Lushin was born in 1951, graduated from N. Bauman Moscow State Technical University in 1974, Dr. Ph., associated professor of sub-faculty "Laser and optical-electronic systems", is the author of 30 scientific publications in the field of development and manufacturing of optical-electronic control devices.
Публикации с ключевыми словами: оптические системы, оптические сигналы
Публикации со словами: оптические системы, оптические сигналы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



