научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#3 март 2008
DOI: 10.7463/0308.0082725
УДК 519.6
Карпенко А.П.
(д.ф.-м.наук, профессор МГТУ им.Н.Э.Баумана, телефон: 263-65-26, E-mail: karpenko@nog.ru)
Федорук В.Г.
(к.т.н., доцентМГТУим.Н.Э.Баумана, телефон: 263-65-26, E-mail: fedoruk@comcor.ru)
1. Введение
Рассматривается один из важнейших частных случаев общей задачи принятия решений - задача непрерывной конечномерной многокритериальной оптимизации в условиях определенности, которую условно можно записать в виде
![]() .
.
Здесь ![]() - множество допустимых значений вектора параметров
- множество допустимых значений вектора параметров ![]() ; вектор
; вектор ![]() - решение задачи;
- решение задачи; ![]() - векторный критерий оптимальности, где общее количество частных критериев mне превышает 10.
- векторный критерий оптимальности, где общее количество частных критериев mне превышает 10.
Выбор критериального языка постановки задачи обусловлен тем, что многокритериальный язык является в настоящее время наиболее полно разработанным. Отметим, что наряду с критериальным языком постановки задачи возможен язык бинарных отношений, а также язык функций выбора [1].
Решение современных многокритериальных задач возможно только в рамках соответствующих автоматизированных систем (MultiCriteriaDecisionMakingSystems - MCDM-систем) с использованием «человекомашинных процедур» [2]. Различают прямые человекомашинные процедуры, адаптивные человекомашинные процедуры, человекомашинные процедуры поиска удовлетворительных решений [3].
Основной идеей прямых человекомашинных процедур является поиск решения путем подбора лицом, принимающим решения (ЛПР), некоторых параметров задачи (например, весов частных критериев оптимальности). Примером программных систем, реализующих прямой метод является система SIGMOP[4]. Прямые процедуры могут быть эффективными только при малом количестве частных критериев (два-три). При большем количестве критериев для ЛПР становится сложно оценивать влияние на решение каждого из весовых множителей. К числу прямых методов относится также метод ELECTRE[5].
В основе адаптивных человекомашинных процедур лежит предположение, что ЛПР может непосредственно сравнивать решения (в критериальном пространстве). Одной из наиболее известных человекомашинных процедур оценки решений является процедура Дайера-Джиофриона [6]. Другим известным методом данного класса является метод Зайонца-Валлениуса [4].
Примером процедур поиска удовлетворительного решения является процедура STEM[5].
В работе рассматриваются адаптивные человекомашинные методы решения задачи многокритериальной оптимизации, основанные на предположении существования «функции предпочтений ЛПР» ![]() , которая определенна на множестве
, которая определенна на множестве ![]() и выполняет его отображение во множество действительных числе R:
и выполняет его отображение во множество действительных числе R:
![]() .
.
При этом задача многокритериальной оптимизации сводится к задаче выбора вектора ![]() такого, что
такого, что
![]() .
.
Часто вместо термина «функция предпочтений» используют термин «функция полезности», иногда – термин «функция потерь» (в этом случае в последней формуле операция максимизации заменяется операцией минимизации).
Предполагается, что при предъявлении ЛПР вектора параметров X, а также соответствующих значений всех частных критериев оптимальности ![]() это лицо может оценить соответствующее значение функции предпочтений
это лицо может оценить соответствующее значение функции предпочтений ![]() .
.
В данной и двух последующих работах указанной серии работ рассматриваются методы аппроксимации функции предпочтений ЛПР, которые лежат в основе предлагаемых в последующих работах адаптивных методов многокритериальной оптимизации. Конечной целью работ является включение соответствующего программного обеспечения в состав программной системы «Парето» [7].
Основное содержание данной работы посвящено методам аппроксимации функции предпочтений ЛПР на основе насыщенных и не насыщенных планов первого порядка.
2. Постановка задачи
Пусть ![]() - n-мерный вектор параметров задачи (вектор варьируемых параметров). Будем полагать, что
- n-мерный вектор параметров задачи (вектор варьируемых параметров). Будем полагать, что ![]() , где
, где ![]() - n-мерное арифметическое пространство (пространство параметров),
- n-мерное арифметическое пространство (пространство параметров), ![]() .
.
Параллелепипедом допустимых значений вектора параметров будем называть не пустой параллелепипед
![]()
![]()
где ![]() ,
,![]() ,…,
,…,![]() ,
,![]() - ограничивающие функции.
- ограничивающие функции.
На вектор X может быть дополнительно наложено ![]() ограничений, формирующих множество
ограничений, формирующих множество
![]() .
.
Множеством допустимых значений вектора параметров Xявляется замкнутое множество
![]()
![]() .
.
Отметим, что параллелепипед П имеет, в основном, «технологический» смысл – определяет диапазоны изменения случайных чисел, формирующих расчетную сетку во множестве ![]() при решении однокритериальной задачи глобальной условной оптимизации, к которой сводится исходная задача многокритериальной оптимизации. Кроме того, параллелепипед П обеспечивает ограниченность и замкнутость множества
при решении однокритериальной задачи глобальной условной оптимизации, к которой сводится исходная задача многокритериальной оптимизации. Кроме того, параллелепипед П обеспечивает ограниченность и замкнутость множества ![]() .
.
Пусть ![]() - векторный критерий оптимальности, определенный на параллелепипеде П, и ЛПР стремится минимизировать каждый из частных критериев оптимальности
- векторный критерий оптимальности, определенный на параллелепипеде П, и ЛПР стремится минимизировать каждый из частных критериев оптимальности ![]() . Будем полагать, что
. Будем полагать, что ![]() , где
, где ![]() - m-мерное арифметическое пространство (пространство критериев),
- m-мерное арифметическое пространство (пространство критериев), ![]() .
.
Множество, в которое векторный критерий оптимальности ![]() отображает множество
отображает множество ![]() , обозначим
, обозначим ![]() и назовем критериальным множеством (множеством достижимости).
и назовем критериальным множеством (множеством достижимости).
Также обозначим ![]() и будем писать
и будем писать ![]() , если
, если ![]() и среди равенств и неравенств
и среди равенств и неравенств ![]() ,
, ![]() имеется хотя бы одно строгое. Вектор
имеется хотя бы одно строгое. Вектор ![]() из критериального множества доминирует по Парето вектор
из критериального множества доминирует по Парето вектор ![]() из того же множества, если
из того же множества, если ![]() .
.
Не формально, множество Парето ![]() поставленной задачи многокритериальной оптимизации можно определить как совокупность векторов
поставленной задачи многокритериальной оптимизации можно определить как совокупность векторов ![]() , среди которых нет доминируемых. Формально, множество Парето определяется следующим образом:
, среди которых нет доминируемых. Формально, множество Парето определяется следующим образом:
![]() .
.
Если ![]() , то будем говорить, что вектор X - эффективный по Парето вектор. Множество векторов, которое порождает множество Парето, обозначается
, то будем говорить, что вектор X - эффективный по Парето вектор. Множество векторов, которое порождает множество Парето, обозначается ![]() и называется эффективным по Парето множеством.
и называется эффективным по Парето множеством.
3. Метод скалярной свертки
Не будем фиксировать способ свертки – это может быть аддитивная свертка, мультипликативная свертка, свертка Джоффриона и другие свертки [1].Обозначим операцию свертки ![]() , где
, где ![]() - вектор весовых множителей,
- вектор весовых множителей, ![]()
![]() - множество допустимых значений этого вектора. Иногда функцию
- множество допустимых значений этого вектора. Иногда функцию ![]() в литературе называют суперкритерием.
в литературе называют суперкритерием.
Таким образом, при каждом фиксированном векторе ![]() метод скалярной свертки сводит решение многокритериальной задачи к решению однокритериальной задачи глобальной условной оптимизации
метод скалярной свертки сводит решение многокритериальной задачи к решению однокритериальной задачи глобальной условной оптимизации
![]() . (1)
. (1)
Отметим, что в силу ограниченности и замкнутости множества ![]() решение задачи (1) существует.
решение задачи (1) существует.
При использовании аддитивной свертки имеет место следующая известная теорема.
Теорема 1. Если для некоторого вектора весовых множителей ![]() и вектора параметров
и вектора параметров ![]() имеет место равенство
имеет место равенство
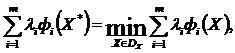 (2)
(2)
то вектор ![]() принадлежит множеству эффективных по Парето векторов.
принадлежит множеству эффективных по Парето векторов.
Для произвольной скалярной свертки точка ![]() , полученная в результате решения задачи (2), вообще говоря, не принадлежит множеству Парето. В этой связи обратим внимание на то, что ЛПР не всегда выбирает решение, принадлежащее множеству Парето [3],
, полученная в результате решения задачи (2), вообще говоря, не принадлежит множеству Парето. В этой связи обратим внимание на то, что ЛПР не всегда выбирает решение, принадлежащее множеству Парето [3],
Обычно в методе скалярной свертки используют нормализованные частные критерии, приводя их к одному масштабу, например, следующим образом:
![]() .
.
Здесь
![]() ,
, ![]() -
-
соответственно, минимальное и максимальное во множестве ![]() значения частного критерия оптимальности
значения частного критерия оптимальности ![]() .
.
Будем полагать далее, что все частные критерии тем или иным способом нормализованы и сохраним за нормализованными частными критериями оптимальности обозначения ![]() .
.
4. Функция предпочтений ЛПР
Если при каждом ![]() решение задачи (1) единственно (а при использовании численных методов это всегда имеет место), то условие (1) ставит в соответствие каждому из допустимых векторов
решение задачи (1) единственно (а при использовании численных методов это всегда имеет место), то условие (1) ставит в соответствие каждому из допустимых векторов ![]() единственный вектор
единственный вектор ![]() и соответствующие значения частных критериев оптимальности
и соответствующие значения частных критериев оптимальности ![]() . Это обстоятельство позволяет полагать, что отношение предпочтения ЛПР определено не на множестве
. Это обстоятельство позволяет полагать, что отношение предпочтения ЛПР определено не на множестве ![]() , а на множестве
, а на множестве ![]() :
:
![]() .
.
В результате задача многокритериальной оптимизации сводится к задаче выбора вектора ![]() такого, что
такого, что
![]() . (3)
. (3)
Обычно размерность пространства критериев во много раз меньше размерности пространства параметров (![]() ), что чрезвычайно важно с точки зрения программной реализации метода.
), что чрезвычайно важно с точки зрения программной реализации метода.
Отметим следующие обстоятельства. Если используется аддитивная свертка (2) и множество достижимости ![]() является выпуклым, то выражение (1) задает взаимно однозначное отображение множества
является выпуклым, то выражение (1) задает взаимно однозначное отображение множества ![]() во множество
во множество ![]() . В этих условиях для любого
. В этих условиях для любого ![]() вектор
вектор ![]() , являющийся решением задачи (1), принадлежит эффективному по Парето множеству
, являющийся решением задачи (1), принадлежит эффективному по Парето множеству ![]() . Если вместо аддитивной свертки используется свертка Джоффриона, реализующая принцип лексикографического упорядочения, то для получения того же результата не требуется выпуклость множества достижимости [1].
. Если вместо аддитивной свертки используется свертка Джоффриона, реализующая принцип лексикографического упорядочения, то для получения того же результата не требуется выпуклость множества достижимости [1].
Величину ![]() будем считать лингвистической переменной со значениями представленными в Табл. 1, где термы есть символы нормальных нечетких подмножеств универсального множества
будем считать лингвистической переменной со значениями представленными в Табл. 1, где термы есть символы нормальных нечетких подмножеств универсального множества ![]() . Напомним, что нормальность нечеткого множества
. Напомним, что нормальность нечеткого множества ![]() означает, что его высота
означает, что его высота ![]()
![]() . Здесь
. Здесь ![]() - функция принадлежности нечеткого множества
- функция принадлежности нечеткого множества ![]() . Ядро (центр)
. Ядро (центр) ![]() нечеткого множества
нечеткого множества ![]() есть величина
есть величина ![]() =
=![]() .
.
Заметим, что выбор девяти градаций лингвистической переменной ![]() является общепринятым и далеко не случаен. Дело в том, что, как показывают многочисленные психофизиологические исследования, человек обычно использует не более девяти вербальных оценок относительной значимости (предпочтительности). Отметим также, что, как показывают те же исследования, оценки на основе лингвистической шкалы надежнее, чем числовые оценки [3].
является общепринятым и далеко не случаен. Дело в том, что, как показывают многочисленные психофизиологические исследования, человек обычно использует не более девяти вербальных оценок относительной значимости (предпочтительности). Отметим также, что, как показывают те же исследования, оценки на основе лингвистической шкалы надежнее, чем числовые оценки [3].
Таблица 1. Допустимые значения функции предпочтений ЛПР, как лингвистической переменной
Функция предпочтений |
|
”Очень-очень плохо” | 1 |
”Очень плохо” | 2 |
”Плохо” | 3 |
”Не совсем удовлетворительно” | 4 |
”Удовлетворительно” | 5 |
”Не совсем хорошо” | 6 |
”Хорошо” | 7 |
”Очень хорошо” | 8 |
”Отлично” | 9 |
В данной работе полагается, что задача многокритериальной оптимизации сведена к задаче отыскания вектора ![]() , обеспечивающего максимальное значение четкой дискретной функции
, обеспечивающего максимальное значение четкой дискретной функции ![]() :
:
![]() . (4)
. (4)
5. Аппроксимация функции предпочтений ЛПР на основе симплекс-планов
Напомним, что симплексом ![]() в пространстве
в пространстве ![]() называется многогранник с M=m+1 вершинами
называется многогранник с M=m+1 вершинами ![]() .
.
Симплекс-план представляет собой насыщенный план первого порядка, т.е. план, предназначенный для оценки коэффициентов линейной регрессии относительно m факторов. Поскольку вершины симплекса Sне лежит ни в одной из ![]() -мерных гиперплоскостей, спектр симплекс-плана имеет Mлинейно независимых строку [8].
-мерных гиперплоскостей, спектр симплекс-плана имеет Mлинейно независимых строку [8].
Построить в пространстве ![]() симплекс
симплекс ![]() - значит определить матрицу координат его вершин. Если первую вершину
- значит определить матрицу координат его вершин. Если первую вершину ![]() правильного симплекса
правильного симплекса ![]() совместить с началом координат, положить длины всех его ребер равными единицы, а сам симплекс сориентировать таким образом, чтобы все его ребра, выходящие из вершины
совместить с началом координат, положить длины всех его ребер равными единицы, а сам симплекс сориентировать таким образом, чтобы все его ребра, выходящие из вершины ![]() , составляли одинаковые углы с координатными осями, то матрица координат вершин симплекса будет иметь следующий вид
, составляли одинаковые углы с координатными осями, то матрица координат вершин симплекса будет иметь следующий вид
 ,
,
где ![]() ,
, ![]() .
.
Если вершина ![]() правильного симплекса
правильного симплекса ![]() находится в точке
находится в точке ![]() , а длина всех его ребер равна
, а длина всех его ребер равна ![]() , то приведенная выше матрица приобретает вид
, то приведенная выше матрица приобретает вид
 .
.
В экстремальных экспериментах на основе симплекс-планов основной операций является операция отражения вершины симплекса [8]. В результате отражения вершины ![]() симплекса
симплекса
![]() (5)
(5)
относительно центра тяжести остальных вершин получаем новый симплекс
![]()
![]() , (6)
, (6)
где
![]() -
-
вектор координат центра тяжести остальных вершин симплекса ![]() (за исключением отраженной вершины
(за исключением отраженной вершины ![]() ).
).
Значения функции ![]() в вершинах симплекса (5) обозначим
в вершинах симплекса (5) обозначим ![]() ,
, ![]() .
.
Легко показать, что коэффициенты линейной функции ![]() , проходящей через точки
, проходящей через точки ![]()
![]() , определяются невырожденной системой Mлинейных алгебраических уравнений (СЛАУ)
, определяются невырожденной системой Mлинейных алгебраических уравнений (СЛАУ)
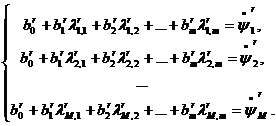 (7)
(7)
Здесь ![]() , а
, а ![]() -матрица
-матрица
Λ=
называется планом эксперимента. Совокупность различных строк этой матрицы называется спектром плана. План эксперимента отличается от спектра плана в случае, когда имеет место дублирование опытов [8]. Отметим, что i-я строка ![]() матрицы Λ представляет собой значения компонентов вектора
матрицы Λ представляет собой значения компонентов вектора ![]() , полученные в
, полученные в ![]() -ом эксперименте.
-ом эксперименте.
Линейная функция ![]() , проходящая через вершины
, проходящая через вершины ![]()
![]() симплекса (6), определяется невырожденной СЛАУ, аналогичной СЛАУ (7).
симплекса (6), определяется невырожденной СЛАУ, аналогичной СЛАУ (7).
Уравнение гиперплоскости, проходящей через общие точки симплексов (5), (6), будем искать в виде ![]() . Из условия прохождения этой гиперплоскости через точки
. Из условия прохождения этой гиперплоскости через точки ![]() , где
, где ![]() , имеем следующую невырожденную СЛАУ для определения коэффициентов
, имеем следующую невырожденную СЛАУ для определения коэффициентов ![]() :
:
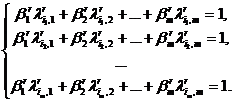
Здесь ![]() .
.
Если построены функции ![]() ,
, ![]() ,
, ![]() , то будем считать, что в полупространстве
, то будем считать, что в полупространстве
![]()
функцию предпочтений ![]() аппроксимирует функция
аппроксимирует функция ![]() , а в полупространстве
, а в полупространстве
![]() -
-
функция ![]() - см. Рис.1. Здесь
- см. Рис.1. Здесь ![]() a – вещественное число.
a – вещественное число.
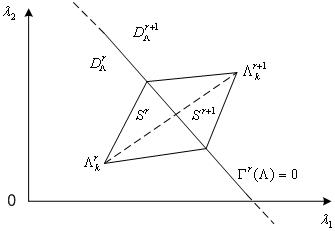
Рис. 1. К аппроксимации функции предпочтений на симплексах ![]() ,
, ![]() :
: ![]()
Аналогично, если путем отражения соответствующих вершин последовательно построены симплексы ![]() ,
, ![]() ,…,
,…,![]() и функции
и функции ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() ,
, ![]() ,…,
,…,![]() , то будем полагать, что в полупространстве
, то будем полагать, что в полупространстве
![]()
функцию предпочтений ![]() аппроксимирует функция
аппроксимирует функция ![]() , в области
, в области
![]() -
-
функция ![]() и т.д. (см. Рис.2). Здесь
и т.д. (см. Рис.2). Здесь ![]() - общее количество симплексов.
- общее количество симплексов.

Рис. 2. К аппроксимации функции предпочтений на симплексах ![]() ,
, ![]() ,
, ![]() :
: ![]()
Приведенная схема аппроксимации учитывает тот факт, что с ростом количества итераций ЛПР обычно оценивает свою функцию предпочтений более точно.
Наряду с рассмотренным правильным симплексом при аппроксимации функции предпочтений могут использоваться неправильные симплексы, полученные путем сжатия и растяжения текущего симплекса.
В результате сжатия симплекса ![]() в направлении
в направлении ![]() получаем новый симплекс
получаем новый симплекс
![]()
![]()
где ![]() - коэффициент сжатия,
- коэффициент сжатия, ![]() - вектор координат центра тяжести остальных вершин симплекса
- вектор координат центра тяжести остальных вершин симплекса ![]() (за исключением сжимаемой вершины
(за исключением сжимаемой вершины ![]() ).
).
В результате растяжения симплекса ![]() в направлении
в направлении ![]() получаем новый симплекс
получаем новый симплекс
![]()
![]()
где ![]() - коэффициент растяжения,
- коэффициент растяжения, ![]() - как и ранее, вектор координат центра тяжести остальных вершин симплекса
- как и ранее, вектор координат центра тяжести остальных вершин симплекса ![]() .
.
В этом случае в число симплексов, на которых строится кусочно-линейная аппроксимация функции предпочтений, включаются только симплексы, предшествующие операциям отражения, а также последний (по порядку построения) симплекс. В примере, приведенном на Рис. 3, аппроксимацию функции предпочтений нужно строить на симплексах ![]() ,
, ![]() ,
, ![]() .
.

Рис. 3. К аппроксимации функции предпочтений на симплексах ![]() ,
, ![]() ,
, ![]()
6. Аппроксимация функции предпочтений на основе регрессионных планов первого порядка
Линейная по параметрам регрессионная модель функции предпочтений имеет вид
![]() ,
,
где ![]() -
- ![]() -мерный вектор-столбец неизвестных коэффициентов,
-мерный вектор-столбец неизвестных коэффициентов, ![]() -
- ![]() -мерный вектор-столбец базисных функций
-мерный вектор-столбец базисных функций ![]() ,
, ![]() - скалярная аддитивная помеха. В случае полиномиальной регрессии в качестве базисных функций используются полиномы и
- скалярная аддитивная помеха. В случае полиномиальной регрессии в качестве базисных функций используются полиномы и
![]() ,
,
![]() ,
,
![]() ,….
,….
Аппарат классического регрессионного анализа [8] исходит из того, что выполнены следующие предпосылки.
1) Аддитивная помеха ![]() есть случайная величина с нулевым математическим ожиданием
есть случайная величина с нулевым математическим ожиданием ![]() и постоянной дисперсией
и постоянной дисперсией ![]() .
.
2) Значения помехи ![]() в различных наблюдениях не коррелированны.
в различных наблюдениях не коррелированны.
3) Ошибка измерения факторов ![]() равна нулю.
равна нулю.
4) Помеха ![]() подчиняется нормальному распределению с параметрами
подчиняется нормальному распределению с параметрами ![]() ,
, ![]() .
.
5) Векторы-столбцы значений базисных функций в матрице ![]() (см. ниже) линейно независимы.
(см. ниже) линейно независимы.
Указанные требования к помехе ![]() необходимы для статистического анализа результатов регрессионного анализа, т.е. для оценки точности найденных коэффициентов регрессии и оценки точности и адекватности регрессионной модели в целом.
необходимы для статистического анализа результатов регрессионного анализа, т.е. для оценки точности найденных коэффициентов регрессии и оценки точности и адекватности регрессионной модели в целом.
Численные значения базисных функций в ![]() опытах обозначим в виде
опытах обозначим в виде ![]() -матрицы
-матрицы
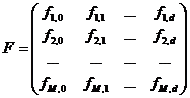 ,
,
где ![]() =
=![]() - значения базисных функций, полученные в
- значения базисных функций, полученные в ![]() -ом опыте.
-ом опыте.
Для определения вектора неизвестных параметров B обычно используется метод наименьших квадратов (МНК), в соответствии с которым параметры ![]() находятся из условия минимума суммы квадратов отклонений измеренных значений выходной переменной
находятся из условия минимума суммы квадратов отклонений измеренных значений выходной переменной ![]() от таких же значений, полученных с помощью регрессионной модели:
от таких же значений, полученных с помощью регрессионной модели:
![]() .
.
Приравнивая нулю первые частные производные левой части этого выражения, получим СЛАУ для определения вектора неизвестных B
![]() ,
,
которая называется системой нормальных уравнений. Здесь симметричная ![]() матрица
матрица ![]() называется информационной матрицей (Фишера) [8],
называется информационной матрицей (Фишера) [8], ![]() -мерный вектор-столбец
-мерный вектор-столбец ![]() ;
; ![]() - значение выходной переменной (отклика) в i-ом эксперименте.
- значение выходной переменной (отклика) в i-ом эксперименте.
Можно показать [8], что если справедливы сформулированные выше предпосылки, то полученные оценки коэффициентов ![]() обладают следующими свойствами:
обладают следующими свойствами:
1) эти оценки являются несмещенными;
2) дисперсия оценки коэффициента ![]() равна
равна ![]() , где
, где ![]() - соответствующий диагональный элемент матрицы, обратной к информационной матрице.
- соответствующий диагональный элемент матрицы, обратной к информационной матрице.
В тех же условиях возможен статистический анализ результатов: 1)проверка значимости оценок коэффициентов регрессии; 2)проверка адекватности регрессионной модели и функции отклика; 3)анализ работоспособности регрессионной модели.
В данном разделе мы рассматриваем планы первого порядка, предназначенные для получения линейных регрессий вида
![]() . (8)
. (8)
Для нахождения оценок неизвестных коэффициентов регрессии ![]() каждый из факторов
каждый из факторов ![]() должен варьироваться в этом случае, по крайней мере, на двух уровнях.
должен варьироваться в этом случае, по крайней мере, на двух уровнях.
Обычно от «натуральных» факторов ![]() переходят к стандартизованным факторам
переходят к стандартизованным факторам ![]() ,
, ![]() ,
, ![]() , где
, где ![]() - основной (базовый) уровень фактора
- основной (базовый) уровень фактора ![]() , а
, а ![]() - шаг варьирования этого фактора. Гиперпараллелепипед
- шаг варьирования этого фактора. Гиперпараллелепипед ![]() ,
, ![]() при этом называется областью планирования эксперимента [8].
при этом называется областью планирования эксперимента [8].
Для нормированных факторов регрессионная модель (8) имеет вид
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() ;
; ![]() ,
, ![]() .
.
Основной проблемой при использовании регрессионных моделей является проблема выбора плана, на основе которого строится регрессия. Этот выбор следует производить между двумя следующими крайними вариантами [8].
1) Планы, близкие к насыщенным планам по количеству точек в спектре. Эти планы требуют небольшого количества испытаний, однако имеют низкую помехозащищенность (если план насыщенный – то сглаживания вообще нет).
2) Планы, близкие к планам, реализующим полный факторный эксперимент (ПФЭ) ![]() . Эти планы требуют большого количества испытаний, но зато обладают высокой помехозащищенностью.
. Эти планы требуют большого количества испытаний, но зато обладают высокой помехозащищенностью.
С учетом сделанных замечаний естественным является выбор, там, где это возможно, плана дробного факторного эксперимента (ДФЭ) ![]() .
.
Ниже приводится библиотека планов для задачи многокритериальной оптимизации, содержащей от 2 до 10 частных критериев оптимальности. Информационная матрица Фишера ![]() , соответствующая каждому из этих планов, является диагональной с диагональными элементами, равными количеству опытов
, соответствующая каждому из этих планов, является диагональной с диагональными элементами, равными количеству опытов ![]() (а, значит, решить соответствующую СЛАУ не представляет труда).
(а, значит, решить соответствующую СЛАУ не представляет труда).
m=2. План ПФЭ ![]() : число опытов M=4; число степеней свободы
: число опытов M=4; число степеней свободы ![]() (см. Табл.2).
(см. Табл.2).
Таблица 2. План ПФЭ ![]() , m=2
, m=2
Номер опыта i |
|
|
|
|
|
| |
1 | 1 | -1 | -1 |
2 | 1 | 1 | -1 |
3 | 1 | -1 | 1 |
4 | 1 | 1 | 1 |
m=3. План ПФЭ ![]() : число опытов M=8; число степеней свободы
: число опытов M=8; число степеней свободы ![]() 4 (см. Табл.3).
4 (см. Табл.3).
Таблица 3. План ПФЭ ![]() , m=3
, m=3
Номер опыта i |
|
|
|
|
|
|
|
| |
1 | 1 | -1 | -1 | -1 |
2 | 1 | 1 | -1 | -1 |
3 | 1 | -1 | 1 | -1 |
4 | 1 | 1 | 1 | -1 |
5 | 1 | -1 | -1 | 1 |
6 | 1 | 1 | -1 | 1 |
7 | 1 | -1 | 1 | 1 |
8 | 1 | 1 | 1 | 1 |
m=4. Ненасыщенный план ДФЭ ![]() : p=1; число опытов M=8; число степеней свободы
: p=1; число опытов M=8; число степеней свободы ![]() 3; ведущие факторы
3; ведущие факторы ![]() ; генерирующее соотношение
; генерирующее соотношение ![]() (см. Табл.4).
(см. Табл.4).
m=5. Ненасыщенный план ДФЭ ![]() : p=2; число опытов M=8; число степеней свободы
: p=2; число опытов M=8; число степеней свободы ![]() 2; ведущие факторы
2; ведущие факторы ![]() ,
, ![]() ,
, ![]() ; генерирующие соотношения
; генерирующие соотношения ![]() ,
, ![]() .
.
m=6. Ненасыщенный план ДФЭ ![]() : p=3; число опытов M=8; число степеней свободы
: p=3; число опытов M=8; число степеней свободы ![]() 1; ведущие факторы
1; ведущие факторы ![]() ,
, ![]() ,
, ![]() ; генерирующие соотношения
; генерирующие соотношения ![]() ,
, ![]() ,
, ![]() .
.
Таблица 4. План ПФЭ ![]() , m=4
, m=4
Номер опыта i |
|
|
|
|
|
|
|
|
|
| |
1 | 1 | -1 | -1 | -1 | 1 |
2 | 1 | 1 | -1 | -1 | -1 |
3 | 1 | -1 | 1 | -1 | -1 |
4 | 1 | 1 | 1 | -1 | 1 |
5 | 1 | -1 | -1 | 1 | 1 |
6 | 1 | 1 | -1 | 1 | -1 |
7 | 1 | -1 | 1 | 1 | -1 |
8 | 1 | 1 | 1 | 1 | 1 |
m=7. Ненасыщенный план ДФЭ ![]() : p=3; число опытов M=16; число степеней свободы
: p=3; число опытов M=16; число степеней свободы ![]() 8; ведущие факторы
8; ведущие факторы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; генерирующие соотношения
; генерирующие соотношения ![]() ,
, ![]() ,
, ![]() .
.
m=8. Ненасыщенный план ДФЭ ![]() : p=4; число опытов M=16; число степеней свободы
: p=4; число опытов M=16; число степеней свободы ![]() 7; ведущие факторы
7; ведущие факторы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; генерирующие соотношения
; генерирующие соотношения ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
m=9. Ненасыщенный план ДФЭ ![]() : p=5; число опытов M=16; число степеней свободы
: p=5; число опытов M=16; число степеней свободы ![]() 6; ведущие факторы
6; ведущие факторы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; генерирующие соотношения
; генерирующие соотношения ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
m=10. Ненасыщенный план ДФЭ ![]() : p=6; число опытов M=16; число степеней свободы
: p=6; число опытов M=16; число степеней свободы ![]() 5; ведущие факторы
5; ведущие факторы ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; генерирующие соотношения
; генерирующие соотношения ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
7. Заключение
В работе рассмотрено использование насыщенных симплекс-планов и не насыщенных регрессионных планов первого порядка для аппроксимации функции предпочтений ЛПР. На основе данных методов в последующих публикациях данной серии работ будут предложены адаптивные методы многокритериальной оптимизации.
Литература
- Черноруцкий И.Г. Методы принятия решений. –СПб.: БХВ-Петербург. 2005. – 416 с.
- Карпенко А.П., Федорук В.Г. Обзор программных систем многокритериальной оптимизации. Отечественные системы. – Информационные технологии, ╧1, 2008, с. 15-22.
- Ларичев О.И. теория и методы принятия решения. -М.: Университетская книга, Логос, 2006. -392 с.
- Штойер Р. Многокритериальная оптимизация. Теория, вычисления и приложения. –М.: Радио и связь, 1992. - 504 с.
- Аннич И., Ларичев О.И. Метод ЭЛЕКТРА и проблема ацикличности отношений альтернатив. - Автоматика и телемеханика, 1996, ╧8, с.108 – 118.
- Дайер Дж. Многоцелевое программирование с использованием человекомашинных процедур // Вопросы анализа и процедуры принятия решений. –М.:Мир, 1976, с.172—215.
- Карпенко А.П., Федорук В.Г. Организация последовательно-параллельной обучающей системы многокритериальной оптимизации «Парето» // Материалы Всероссийской научной конференции «Информационные технологии в науке, образовании и производстве», Казань, 2007, с. 618 – 620.
- Грачев Ю.П., Плаксин Ю.М. Математические методы планирования эксперимента. –М.: Издательство ДеЛи принт, 2005. - 296 с.
- Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации. –М.: Издательство МГТУ им. Н.Э.Баумана, 2001. – 440 с.
Публикации с ключевыми словами: аппроксимация, многомерная оптимизация, многокритериальная оптимизация
Публикации со словами: аппроксимация, многомерная оптимизация, многокритериальная оптимизация
Смотри также:
- Аппроксимация функции предпочтений лица, принимающего решения, в задаче многокритериальной оптимизации. Методы на основе планов второго порядка
- Исследование погрешности нейросетевой аппроксимации функции предпочтений
- Исследование погрешности аппроксимации многомерной функции с помощью нейронных сетей с радиальными базисными функциями
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



