научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2014
DOI: 10.7463/0114.0696028
УДК: 519.2
| УДК 519.2 | Россия, МГТУ им. Н.Э. Баумана |
Введение
В настоящее время все чаще специалисты по информационным технологиям становятся активными участниками решения проблем здоровья людей. Однако это предполагает, что специалисты по информационным технологиям имеют достаточный объём соответствующих медицинских знаний, чтобы вести разработки информационных систем, предметной областью которых является медицина. Весьма привлекательными подобные информационные системы являются в тех случаях, когда они способствуют сохранению здоровья у практически здоровых людей. Подобные системы получили название “Навигаторы здоровья”. В таких системах, например, заинтересованы медицинские страховые компании и поликлиники для проведения экспресс – обследования клиентов и пациентов.
Одной из ключевых задач при создании информационных систем типа “Навигатор здоровья” является выбор измеряемых параметров человека при его обследовании и разработка алгоритмов обработки результатов измерении. Во всем многообразии возможных вариантов решения этой задачи хотелось бы выбрать в некотором смысле наилучший вариант и его использовать. Критериями отбора измеряемых параметров, процедур измерения и расчетов отдельных показателей могут быть, например, простота выполнения измерения, надежность измерения, чувствительность, воспроизводимость.
1. Метод анализа
Приведенный анализ 480 мальчиков в возрасте от 14 до 17 лет в медицинской компании «Народный Спорт Парк» [11] применен в данной работе. Выборка по каждой группе составляла 120 человек. На основе полученных результатов анализа прогнозируем физическую работоспособность человека (PWC170/кг), который является одним из важнейших компонентов физического здоровья человека, характеризующим способность организма эффективно выполнять большую мышечную работу и противостоять утомлению. Уровень общей выносливости определяется возможностями мышечной, дыхательной, сердечнососудистой, нервной, эндокринной систем, слаженность их работы при физических нагрузках и, в конечном счете, может служить обобщенной оценкой физического состояния организма.
После измеренияморфологических и функциональных показателей физического здоровья человека проведем анализ полученных результатов. Именно, предполагается построить прогноз значений параметра PWC с помощьюмножественной регрессии. В этом случае необходимо выяснить математическую зависимость физической работоспособности человека от измеряемых морфологических и функциональных показателей.
В математическом смысле это можно свести к типичной задаче многофакторного регрессионного анализа. Идея многофакторного анализа проста. Есть морфологические измеряемые показатели человека. Это – факторы или независимые переменные (их может быть достаточно много, в нашем случае 12), и есть, зависящая от них, зависимая переменная или отклик Y, т.е PWC. У каждого человека имеется свой набор значений морфологических показателей и своя, соответствующая этому набору, физическая работоспособность PWC.
Напомним, что классический многофакторный регрессионный анализ опирается на некоторую систему постулатов в основном статистического характера. Кроме того, предполагается, что это – нормально распределенные случайные величины, поскольку отклонения от среднего равновероятны и в ту и другую сторону. Такая основа позволяет благополучно довести до числа процесс получения оценок регрессионных коэффициентов и осуществить проверки основных статистических гипотез об уравнении регрессии, его коэффициентах и прогнозируемых значениях отклика. В рамках этой гипотезы можно предположить, что отклик (PWC) связан с морфологическими и функциональными показателями (факторами) соотношением
![]() (1)
(1)
где Y - отклик (зависимая переменная), B0 - оценка постоянной составляющей,Bi – i-ый коэффициент множественной регрессии (![]() ), Xi – i-ая независимая переменная, ε – ошибка.
), Xi – i-ая независимая переменная, ε – ошибка.
В данном случае, для анализа используются двенадцать морфологических и функциональных показателей для группы девочек и мальчиков в возрасте от 14 до 17 лет, представленных в таблице 1.
Таблица 1. Параметры для регрессионного анализа
Символ | Определение символа | Сокращение Определения символов |
Y | отклик (PWC170- физическая работоспособность) кгм/кг в мин | PWC170/кг |
| жизненная емкость легких , мл | ЖЕЛ |
| пульс в покое (частота сердечных сокращений, уд/мин) | ЧСС |
| систолическое артериальное давление, мм.рт.ст. | АД-С |
| диастолическое артериальное давление, мм.рт.ст. | АД-Д |
| задержка дыхания, сек | Гипокс. |
| весоростовой коэффициент (Кетле), гр/см | Кетле |
| гибкость позвоночника, см | Гибк. |
| координация движения (бросание в стену теннисных мячей, количество пойманных мячей из 6) | Коорд |
| зрительно-двигательная реакция (тест с падающей линейкой, см) | ЗРД |
| мышцы плечевого пояса (отжимание) | Отжим |
| мышцы брюшного пресса (пресс) | Пресс |
| тест Руфье (приседание) | Руфье |
По существу, это означает, что одному и тому же набору независимых переменных с полным правом могут соответствовать разные значения отклика. Действительно, трудно представить двух человек, имеющих одинаковый набор морфологических показателей и одинаковую же физическую работоспособность. Такая вариация может иметь место из-за ошибок измерения, но, прежде всего это, конечно, является следствием разброса индивидуальных показателей физического состояния человека. Поэтому не приходиться ожидать никакого единственно однозначного уравнения связи между независимыми переменными и откликом. Однако можно обнаружить, что средний наблюдаемый отклик при заданных значениях независимых переменных будет достаточно устойчив.
Поскольку точность определения среднего значения выборки растет с ростом объема выборки, то точность определения коэффициентов регрессионной модели растет с увеличением числа экспериментов, которое не может быть меньше, чем число коэффициентов требующих определения.
Теперь уравнение (1) можно записать для произвольного отклика в виде
![]() (2)
(2)
из которого следует, что для любого набора значений X соответствующее значение Y состоит из величины b0 + b1x1 +b2x2 +…+bnxn + ![]() , с учетом которой любой индивидуальный Y получает возможность не попасть на поверхность регрессии, олицетворяющей собой набор средних значений Y.
, с учетом которой любой индивидуальный Y получает возможность не попасть на поверхность регрессии, олицетворяющей собой набор средних значений Y.
Задачу по построению первого приближения многофакторной регрессионной модели можно считать законченной, если по результатам экспериментов получены оценки коэффициентов уравнения (2) b0,…,bn.
В литературе по регрессионному анализу [1-7] достаточно подробно описан матричный подход и нахождению оценок коэффициентов регрессионной модели. Введем следующие обозначения:
![]() – вектор столбец наблюдений, размерность m×1;
– вектор столбец наблюдений, размерность m×1;
x – матрица независимых переменных, размерность m×n;
b– вектор столбец параметров, подлежащих оцениванию, размерность n×1;
ε– вектор столбец ошибок, размерность m×1;
m – число экспериментов;
n – число коэффициентов, подлежащих оцениванию;
Тогда линейную модель [1-7], подлежащую оцениванию на основе экспериментальных данных, можно записать в форме
![]() (3)
(3)
Используя метод наименьших квадратов [1-6], получаем
![]() (4)
(4)
где ![]() – транспонированная матрица независимых переменных,
– транспонированная матрица независимых переменных, ![]() – обратная матрица, Y – вектор наблюдений.
– обратная матрица, Y – вектор наблюдений.
Таким образом, имея результаты многократного эксперимента (m >n), можно определить коэффициенты b0, b1, … , bn. Величина коэффициентов указывает степень влияния того или иного фактора на отклик, иными словами на зависимость PWC от морфологических и функциональных показателей человека.
Согласно процедуре множественного регрессионного анализа, в первую очередь,необходимо знать каккаждый из независимых параметров xi коррелирует сзависимым параметром PWC [1-7]. Оценивать эту корреляцию предлагается с помощью линейной регрессии, описывающей зависимость между параметром xi и параметром PWC. После оценки зависимости в виде линейной регрессии между каждым параметром xi и параметром PWC можно высказать качественные суждения о характере этих зависимостей.
2. Регрессионный анализ для шестнадцати летних мальчиков
Рассмотрим приведенные результаты анализа для 120-ти шестнадцатилетних мальчиков. На рис 1 в качестве примера приведен результат расчета линейной регрессии между независимым параметром теста Руфье (приседание) и зависимым параметром PWC (PWC170/кг).

Рис. 1. Точечная диаграмма для физической работоспособности и теста Руфье (30 приседаний за 45 сек)
На рис 1 приведены точечная диаграмма, в которых можно рассмотреть линейную регрессию между независимым параметром приседания и зависимым параметром PWC (PWC170/кг). Очевидно, что имеет отрицательная линейная зависимость между этими параметрами. Степень влияния конкретного независимого параметра xi оценивается значением коэффициента детерминации R2. Оказывается, что для параметра х12 (приседание) значение коэффициента детерминации R2 составляет всего 23%. Другими словами, влияние независимого параметра теста Руфье (х12) на зависимый параметр PWC является слабым. Аналогично были получены зависимости между остальными 11 морфологическими и функциональными параметрами и параметром PWC.
Слабая связь корреляции между PWC и независимыми параметрами (таб.2) не является существенными параметрами. Была вычислена корреляционная зависимость между перечисленными выше морфологическими и функциональными параметрами. Приведены результаты корреляционной матрицы и оценки корреляционных зависимостей между рассматриваемыми параметрами в таблице 2.
Таблица. 2. Таблица корреляционной матрицы для всех показателей 16 летних мальчиков
| ЖЕЛ | ЧСС | АД-С | АД-Д | Гипокс. | Кетле | Гибк. | Коорд | ЗРД | Отжим | Пресс | Руфье | PWC170/кг |
ЖЕЛ | 1,000 |
|
|
|
|
|
|
|
|
|
|
|
|
ЧСС | 0,013 | 1,000 |
|
|
|
|
|
|
|
|
|
|
|
АД-С | 0,328 | 0,123 | 1,000 |
|
|
|
|
|
|
|
|
|
|
АД-Д | 0,260 | 0,122 | 0,402 | 1,000 |
|
|
|
|
|
|
|
|
|
Гипокс. | 0,275 | -0,094 | -0,013 | 0,083 | 1,000 |
|
|
|
|
|
|
|
|
Кетле | 0,346 | 0,211 | 0,331 | 0,171 | -0,101 | 1,000 |
|
|
|
|
|
|
|
Гибк. | -0,039 | -0,079 | -0,127 | -0,178 | 0,036 | -0,017 | 1,000 |
|
|
|
|
|
|
Коорд | -0,023 | 0,026 | 0,070 | 0,059 | 0,131 | 0,023 | 0,017 | 1,000 |
|
|
|
|
|
ЗРД | 0,160 | -0,180 | 0,088 | 0,077 | 0,151 | -0,072 | -0,171 | -0,212 | 1,000 |
|
|
|
|
Отжим | 0,009 | -0,017 | -0,071 | -0,239 | -0,023 | 0,083 | 0,195 | -0,063 | -0,187 | 1,000 |
|
|
|
Пресс | 0,054 | -0,046 | -0,087 | -0,189 | 0,020 | 0,056 | 0,111 | -0,192 | 0,007 | 0,521 | 1,000 |
|
|
Руфье | 0,136 | -0,080 | 0,006 | -0,085 | 0,098 | 0,086 | 0,012 | -0,146 | -0,009 | 0,066 | 0,073 | 1,000 |
|
PWC170/кг | 0,083 | -0,251 | 0,126 | 0,047 | -0,003 | -0,126 | -0,001 | 0,122 | 0,078 | 0,073 | 0,028 | -0,484 | 1,000 |
После рассмотрения таблицы корреляции запускаем регрессионный анализ (использовано программное обеспечение MSExcel и SPSS). В этом случае после вычисления результатов регрессионного анализа, в первую очередь нужно проверить, что полученная модель является статистически значимой. Для этого можно использовать метод дисперсионного анализа. Напомним, что дисперсионный анализ позволяет выявить зависимости в экспериментальных данных путём исследования значимости различий в средних значениях. В случае линейной регрессии используются понятия общей дисперсией, объясненной дисперсии и необъясненной дисперсии (рис 2). Если она существенно уменьшает значение необъясненной дисперсии, можем сказать, что полученная в эксперименте линия регрессии является полезным.
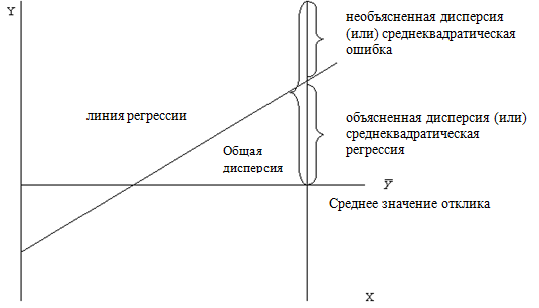
Рис. 2. Диаграмма для объяснения о дисперсии регрессионной модели
Выяснить полезность линии регрессии можно с помощью величины F - статистики. F - статистика является отношением объясненной дисперсии (среднеквадратическая регрессия) и необъясненной дисперсии (среднеквадратическая ошибка). В этом случае объясненную дисперсию или среднеквадратическую регрессию (MSR - MeanSquaredRegression) можно вычислить по формуле [2-7]
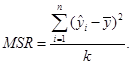 (5)
(5)
Необъясненная дисперсия или среднеквадратическая ошибка (MSE- MeanSquaredError) вычисляет по формуле [2-7]
 (6)
(6)
Здесь MSR – среднеквадратическая регрессия (объясненная дисперсия), MSE – среднеквадратическая ошибка (необъясненная дисперсия), ![]() – i-ая зависимая переменная PWC (
– i-ая зависимая переменная PWC (![]() ),
), ![]() – i-ое предсказанное значение параметра (
– i-ое предсказанное значение параметра (![]() ),
), ![]() – среднее значение зависимой переменной, k – количество регрессоров, n – количество наблюдения.
– среднее значение зависимой переменной, k – количество регрессоров, n – количество наблюдения.
Величину F– статистику можно вычислить по формуле [2-7]
 (или)
(или) ![]() (7)
(7)
Для проверки значимости модели будем использовать F таблицы распределения. В нашем случае, использование F - критерия сводится к сравнению величины F – статистики со значением F – критерий в F – таблице. В случае если вычисленная величина F – статистики больше или равна критической величине F - критерий в F - таблице, то можно сделать вывод, что регрессионная модель является статистически значимой [2-7, 9]. В таблице 3 приведены результаты дисперсионного анализа.
Таблица. 3. Дисперсионный анализ (ANOVA) для 16 – летних мальчиков
Степень свободы | Сумма квадратов | Дисперсия на степень свободы (среднее квадратов) | F | Значимость F | |
Факторная (Регрессии) | 12 | 404,6196 | 33,7183 | 5,7168 | 0,0000 |
Остаточная | 107 | 631,0991 | 5,8981 | ||
Общая | 119 | 1035,7187 |
Таким образом, для множественной регрессионной модели шестнадцатилетних мальчиков вычисленная F– статистика равна 5,7168, и из F-таблицы распределения F – критерия равна 1,8337 [9]. Отсюда следует, что величина F – статистики больше чем, величина F – критерия в F – таблице распределения, и чторегрессионная модель является статистической значимой и полезной.
Попробуем количественно оценить, насколько полезна полученная множественная регрессионная модель для прогнозирования параметра PWC. Другими словами, какую часть в величине прогноза параметра PWC обосновывает множественная регрессионная модель.
Для указанного количественного оценивания полезности полученной множественной регрессионной модели была сделана попытка воспользоваться коэффициентом детерминации R2 [2-7]. Для того чтобы была возможность сравнивать модели с разным числом факторов, так чтобы число факторов (регрессоров) не влияло на значение ![]() , обычно используется скорректированный коэффициент детерминации. Коэффициент детерминации R2 и скорректированный коэффициент детерминации R2aможно вычислить по формулам
, обычно используется скорректированный коэффициент детерминации. Коэффициент детерминации R2 и скорректированный коэффициент детерминации R2aможно вычислить по формулам
 (8)
(8)
![]() (9)
(9)
где ![]() – i-ое значение зависимой переменной PWC (
– i-ое значение зависимой переменной PWC (![]() ),
), ![]() – i-ое предсказанное значение параметра PWC(
– i-ое предсказанное значение параметра PWC(![]() ),
), ![]() – среднее значение зависимой переменной PWC, k – количество регрессоров, n – количество наблюдений.
– среднее значение зависимой переменной PWC, k – количество регрессоров, n – количество наблюдений.
Для шестнадцатилетних мальчиков, вычисленное значение коэффициента детерминации R2 равно 0,39 (или 39%), а скорректированного коэффициента детерминации R2a равно 0,32 (или 32%). Таким образом, в величине прогноза параметра PWC, многофакторная модель обосновывает 32% дисперсии.
Оценим качество модели с помощью стандартной ошибки оценки S![]() , вычисляемой по формуле [2-7]:
, вычисляемой по формуле [2-7]:
 (10)
(10)
Дляшестнадцатилетних мальчиков, вычисленный результат значения стандартной ошибки оценки S![]() равен 2,428. В таблице 4 приведены выводы регрессионного анализа.
равен 2,428. В таблице 4 приведены выводы регрессионного анализа.
Таблица. 4. Регрессионный вывод для 16 - летних мальчиков
Модель | R | R2 | R2a | Стандартная ошибка оценки |
16 мальчиков | 0,625 | 0,390 | 0,322 | 2,428 |
В таблице 5 иллюстрированы вычисленные результаты коэффициентов регрессии, величины т-статистики и т.д. По таблице можем создать регрессионную модель, используя соотношение (2). В этом случае проверяются вычисленные величины коэффициентов регрессии, которые являются статистическими значимыми. Для ответа на поставленный вопрос использовались следующие показатели: стандартная ошибка каждого из коэффициентов регрессии, т – статистика и Р – значение (P-value), которые оченьважны для проверки гипотез значимости каждого из коэффициентов. Для проверки гипотез на самом деле нужно знать значение т – статистики каждого коэффициента, поскольку т – статистика позволяет проверить значимости каждого из коэффициентов регрессии [1-7]. В частности, т – статистику для каждого коэффициентов можно вычислить с помощью стандартной ошибки каждого из коэффициента регрессии. Следовательно, в первую очередь нужно вычислить стандартные ошибки коэффициентов регрессии. Для вычисления стандартной ошибки коэффициентов b0, b1, … , b11 используется формула [1-7]
![]() (11)
(11)
где 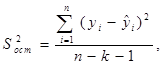 (12)
(12)
S(b) –стандартная ошибка регрессионных коэффициентов, ![]() – обратная матрица,
– обратная матрица, ![]() i –измеряемые значения PWC (зависимая переменная),
i –измеряемые значения PWC (зависимая переменная), ![]() – i-ое предсказанное значение параметра PWC, (i=1,…,n), k – степень свободы регрессии или число регрессоров, n – количество наблюдений.
– i-ое предсказанное значение параметра PWC, (i=1,…,n), k – степень свободы регрессии или число регрессоров, n – количество наблюдений.
Затем можно вычислить т-статистику для каждого коэффициента по формуле [1-6]
 (13)
(13)
где t(b) - т-статистика одного коэффициента, b - коэффициент регрессии, ![]() - стандартная ошибка коэффициента регрессии.
- стандартная ошибка коэффициента регрессии.
Для проверки гипотез значимости коэффициента будем использовать критерий Стьюдента. В нашем случае использование критерия Стьюдента (Т-критерия) сводится к сравнению значении т-статистики со значение Т-критерий в Т-таблице [2-8]. В случае если вычисленное т-значение больше или равно критическому значению Т в Т-таблице, можно сделать вывод, что регрессионный коэффициент является статистическим значимым.
В таблице 5 значения т-статистики (tb1,b2,b3,b6,b12)по сравнению со значением Т-критерия (tтабл = 1,645 (n=120, α=0,05%)) получаются большими.Соответственно коэффициенты т-статистики являются статистическими значимыми. И коэффициенты т-статистики соответствуют следующим физиологическим параметрам: жизненная емкость легких, частота сердечных сокращений, систолическое артериальное давление, весоростовой коэффициент и тест Руфье (приседание). Также рассмотрена проверка мультиколлинеарности в таблице 5. В этом случаемультиколлинеарность представляет собой статистический феномен, в котором два или более регрессоров сильно коррелируют в модели множественной регрессии. Для этого проверяется мультиколлинеарность с использованием VIF(Variance Inflation Factor). Если VIF больше пяти, то мультиколлинеарность существует в модели, которая является не правильной. Все величины VIF меньше пяти. Поэтому мультиколлинеарность отсутствует в модели. Для вычисления VIF можно использовать формулу [7]
 (14)
(14)
где VIF - отклонение коэффициента инфляции (VarianceInflationFactor), ![]() - стандартное отклонение xj ,
- стандартное отклонение xj , ![]() -стандартная ошибка коэффициента регрессии,
-стандартная ошибка коэффициента регрессии, ![]() - средне-квадратическая остаточная.
- средне-квадратическая остаточная.
Для группы из 120 мальчиков шестнадцать лет были вычислены коэффициенты b0 .. b12 с использованием формулой (4). В таблице 5 приведены вычисленные результаты стандартных ошибок коэффициентов регрессии, т-статистики , P-value и коллинеарность для 16 - летних мальчиков.
Таблица. 5. Коэффициенты регрессионного анализа, стандартные ошибки коэффициентов регрессии, т - статистики , P-value и коллинеарность для 16 - летних мальчиков
коэффициенты | стандартные ошибки | т-статистики | P-value | Коллинеарность статистика | ||
толерантность | VIF | |||||
Констант | b0= 19,7322 | 3,3330 | 5,9203 | 0,0000 | ||
ЖЕЛ | b1= 0,0007 | 0,0004 | 1,8409 | 0,0684 | 0,691 | 1,448 |
ЧСС | b2= -0,0634 | 0,0179 | -3,5453 | 0,0006 | 0,896 | 1,116 |
АД-С | b3= 0,0388 | 0,0206 | 1,8862 | 0,0620 | 0,727 | 1,375 |
АД-Д | b4= -0,0070 | 0,0305 | -0,2296 | 0,8188 | 0,739 | 1,352 |
гипокс. | b5= -0,0054 | 0,0104 | -0,5245 | 0,6010 | 0,857 | 1,167 |
Кетле | b6= -0,0089 | 0,0053 | -1,6870 | 0,0945 | 0,747 | 1,338 |
гибк. | b7= -0,0066 | 0,0297 | -0,2234 | 0,8237 | 0,911 | 1,098 |
коорд | b8= 0,0507 | 0,0585 | 0,8681 | 0,3873 | 0,936 | 1,068 |
ЗРД | b9= 0,0050 | 0,0312 | 0,1598 | 0,8733 | 0,844 | 1,185 |
отжим | b10= 0,0379 | 0,0291 | 1,3024 | 0,1956 | 0,662 | 1,510 |
пресс | b11= 0,0077 | 0,0443 | 0,1744 | 0,8619 | 0,700 | 1,429 |
Руфье | b12= -0,6635 | 0,1015 | -6,5345 | 0,0000 | 0,940 | 1,064 |
Уравнение для предсказания значения параметра PWC согласно таблице 5 и формуле (2) имеет вид
 (15)
(15)
где ![]() –предсказанное значение параметра PWC,
–предсказанное значение параметра PWC, ![]() – независимые переменные (таблица 1).
– независимые переменные (таблица 1).
В этом случае без использования незначимых параметров перезапускаем регрессию. Предлагается, что модель со всеми предикторами называется полной моделью. А модель, которая содержит лишь некоторые из этих предсказателей, называется уменьшенной моделью. После перезапуска регрессии рассматривается значимость модели.
В таблице 6 видно, что F – статистика равна 20,4478 и нужно сравнить с F критерий в F таблице распределения. Значение F-статистики (20,4478) больше чем, значение Fтабл. (2,682). Соответственно, будем считать, что можно отвергнуть нулевую гипотезу и уменьшенная регрессионная модель является статистической значимой.
Кроме того, для изменчивости модели рассмотрим вычисленное значение скорректированного коэффициента детерминации R2a. В таблице 7 показано, что значение R2a равно 0,328 (32,8%), уравнение регрессии составляет 32,8% дисперсиирезультативного признака.
В таблице 8 представлены вычисленные регрессионные коэффициенты для модели, с помощью которых получается регрессионная модель (16), используя соотношение (4). После этого выполняется проверка гипотезы для коэффициента регрессии. В таблице 8 т- статистики всех коэффициентов b больше tтабл = 1,645 (n=120, α=0,05%). Следовательно,все коэффициенты являются статистическими значимыми. Проверяются мультиколлинеарности для уменьшенной модели (таб.8), все величины VIF меньше чем пять. Соответственно, мультиколлинеарность отсутствует в модели. В таблицах 6, 7 и 8 приведены результаты для уменьшенной регрессионной модели.
Таблица. 6. Результаты дисперсионного анализа (ANOVA) для 16 -летних мальчиков
Степень свободы | Сумма квадратов | Дисперсия на степень свободы (среднее квадратов) | F | Значимость F | |
Факторная (Регрессии) | 3 | 358,2573 | 119,4191 | 20,4478 | 0,0000 |
Остаточная | 116 | 677,4613 | 5,8402 | ||
Общая | 119 | 1035,7187 |
Таблица. 7. Результаты регрессионной оценки для 16 - летних мальчиков
Модель | R | R2 | R2a | Стандартная ошибка оценки |
16 мальчиков | 0,588 | 0,345 | 0,328 | 2,416 |
Таблица. 8. Коэффициенты регрессионного анализа, стандартные ошибки коэффициентов регрессии, т-статистики , P-value и коллинеарность для 16 - летних мальчиков
| коэффициенты | стандартные ошибки | т-статистики | P-value | Коллинеарность статистика | |
Толерант-ность | VIF | |||||
Констант | b0= 19,7489 | 2,6759 | 7,3801 | 0,0000 | ||
ЧСС | b1= -0,0699 | 0,0170 | -4,1060 | 0,0001 | 0,979 | 1.022 |
АД-С | b2= 0,0389 | 0,0176 | 2,2118 | 0,0289 | 0,985 | 1.016 |
Руфье | b3= -0,6590 | 0,0974 | -6,7667 | 0,0000 | 0,993 | 1.007 |
Уравнение для предсказания значения параметра PWC согласно таблице 8 и формуле (2) имеет вид
![]() (16)
(16)
По результатам сравнения полной модели с уменьшенной моделью (17) оказывается, что уменьшенная модель является лучше полной модели.
 (17)
(17)
Здесь SSR – сумма квадратов регрессии, МSE – среднеквадратическая остаточная, q – разница между количествами регрессоров из двух модели.
3. Анализ остатков
Проанализированы остатки уменьшенной модели. Для проверки анализа остаток рассматривается стандартизированная остаточная гистограмма, в которой показаны остатки нормального распределения и общая форма является приемлемой. Применяя результаты тестов по математическому подходу Колмогорова-Смирнова и Shapiro-Wilk (таб.9) то есть величины значимости больше чем 0,05, починяются остатки по нормальному распределению. На рис. 3 приведены результаты проверки нормальности остатков.
![]()
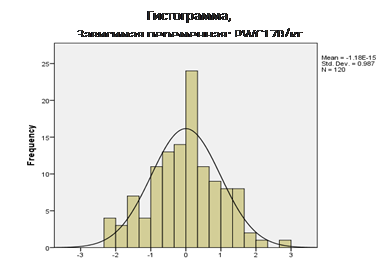
Рис 3. Гистограмма стандартизированных остатков
Таблица. 9. Результаты тестов Колмогорова Смирнова и Shapiro-Wilk
| Колмогоров-Смирнов | Shapiro-Wilk | ||||
Статистика | df | Значи-мость. | Статистика | df | Значи-мость | |
Cтьюдентизированные остаточные | 0,056 | 120 | 0,200* | 0,991 | 120 | 0,651 |
Стандартизированные остаточные | 0,055 | 120 | 0,200* | 0,991 | 120 | 0,665 |
Рассмотрим привертку гетероскедастичность модели. Под гетероскедастичностью понимают неравные дисперсии остаток модели (проблема в дисперсии остатков). В противном случае гетероскедастичность отсутствует гомоскедастичность, т.е равные дисперсии остаток. Можно проверить гетероскедастичность с использованием теста Бройша Пагана, теста Голдфелда, Уайта, Коэнкера и.т.д. Рассматривая точечную диаграмму по диаграмме 4 для проверки гетероскедастичности остатков, в этой остаточной точечной диаграммы отсутствует шаблон.Если проверить гетероскедастичность с помощью теста Бройша Пагана, т.е по математическому подходу, остаточный квадрат от регрессионной модели становится зависимой переменной. И запускаем регрессионный анализ с остаточным квадратом и регрессорами уменьшенной модели. Получена величина Бройша Пагана по умножению количества наблюдений на полученный коэффициент детерминации. После вычисления, сравнивая величину Бройша Пагана с критерием хи-квадрат в таблице распределения хи-квадрата, получим величину Бройша Пагана = 3,442 и критерий хи-квадрат в таблице = 7,815. Очевидно, что величина Бройша Пагана меньше критерия хи-квадрат, что означает, отсутствует гетероскедастичность в уменьшенной регрессионной модели. На рис 4 приведена точечная диаграмма стандартизированных остатков для проверки гетероскедастичности.


Рис. 4. Точечная диаграмма стандартизированных остатков
Введем автокорреляцию, т.е статистическая взаимосвязь между последовательностями величин одного ряда, взятых со сдвигом, например, дляслучайного процесса со сдвигом по времени. В этом случае, используем тест Дарбина Уотсона для обнаружения автокорреляции. Если остаточный et связан с наблюдением в момент времени T, можно записать тест статистики вида
 (18)
(18)
где Т-число наблюдений, et – остатки регрессионной модели.
Для проверки положительной автокорреляции на значении α тестовая статистика d по сравнению с нижним и верхним критическим значением из таблицы Дарбина Уотсона (dL,α and dU,α) должна удовлетворять условиям:
· если d <dL, при α=0,05, имеется статистические доказательства, что ошибки терминов положительно автокоррелированы;
· если d >dU, при α=0,05, отсутствуют статистические доказательства того, что ошибки терминов положительно автокоррелированы;
· если dL, α < d < dU, при α=0,05, тест является не решенным.
Таким образом, по тесту Дарбина Уотсона d = 2,057 и в таблице указывается d нижняя =1,584 , d верхняя = 1,665 для трех степеней свободы. Поэтому величина Дарбина Уотсона d > d верхняя и можно считать, что положительная автокорреляция отсутствует в модели.
В результате можно сделать вывод, что по проверке гипотеза данной статьи (F-тест, t-тест, и.т.д) модель множественной регрессии физической работоспособности шестнадцатилетних мальчиков является полезной и найдено применение для оценки состояния здоровья подростков. Даже независимые и зависимые переменные имеют слабую корреляцию. Другие регрессионные модели для 14 -, 15 - и 17 - летних мальчиков также позволяют получить аналогичные результаты.
Заключение
Для прогнозирования физического здоровья мальчиков выбран метод множественного регрессионного анализа статистики, который позволяет проводить анализ многофакторных статистических моделей. Разработаны математические и статистические модели для прогнозирования физического здоровья мальчиков в возрасте от четырнадцати до семнадцати лет. Определены значимые параметры для математических моделей прогнозирования, с помощью которых можно быстро и эффективно оценить физическое здоровье мальчиков в возрасте от четырнадцати до семнадцати лет. По результатам регрессионного анализа регрессионные модели мальчиков в возрасте от четырнадцати до семнадцати лет являются статистически значимыми и могут быть использованы при оценке состояния здоровья. Найдены значимые параметры для оценки физической работоспособности прогнозирования физического здоровья мальчиков в возрасте от четырнадцати до семнадцати лет.
Список литературы
- Вапник В.Н. Восстановление зависимостей по эмпирическим данным. М.: Наука, 1979. 448 с.
- Edelmann-Nusser J., Hohmann A., Bügner J., Witte K. Modeling performance upon neural networks // In: Current trends in performance analysis: World Congress of Performance Analysis of Sport. Aachen: Shaker, 2009. P.349-357.
- Корнеева И.Т., Поляков С.Д., Гоготова В.Л., Петричук С.В., Дворяковская Г.М., Дворяковский И.И., Изотова И.Н. Математические подходы оценки адаптации кардиогемодинамики в зависимости от активности клеточных дегидрогеназ лимфоцитов крови у юных спортсменов // Лечебная физкультура и спортивная медицина. 2009. № 9. С. 28-32.
- Горяинов В.Б., Павлов И.В., Цветкова Г.М., Тескин О.И. Математическая статистика: учеб. для вузов. 2-е изд., стер. М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. 424 с. (Сер. Математика в техническом университете; вып. XVII).
- Rawlings J.O., Pentula S.G., Dickey D.A. Applied regression analysis. A research tool. 2nd ed. Springer-Verlag, 1998. 659 p. (Ser. Springer texts in statistics).
- Freedman D.A. Statistical Models: Theory and Practice. Cambridge University Press, 2005. 414 p.
- Kam C.D., Franzitsi Jr. R.J. Modeling and interpreting interactive hypotheses in regression analysis. University of Michigan Press, 2009. 168 p.
- Chatterjee S., Hadi A.S. Regression analysis by example. 4th ed. Wiley, 2006. 366 p. (Wiley series in probability and statistics).
- Pedhazur E.J. Multiple regression in behavioral research: Explanation and prediction. 3rd ed. Thomson Learning, 1997. 1072 p.
- Hoffmann J.P. Linear Regression Analysis: Assumptions and Applications. Department of Sociology Brigham Young University, 2005. 259 p.
- Six sigma online. Режим доступа: http://sixsigmaonline.ru/load/24-1-0-210(дата обращения 20.11.2013).
- Google document Т-таблица. Режим доступа: https://docs.google.com/viewer?a=v&q=cache:1boQad1pHCQJ:www.sjsu.edu/faculty/gerstman/StatPrimer/t-table.pdf(дата обращения 20.11.2013).
- Statistics Online Computational Resource (SOCR). Режим доступа: http://socr.ucla.edu/Applets.dir/F_Table.html(дата обращения 20.11.2013)
- Народный СпортПарк. Режим доступа: http://sportpark.ru/ (дата обращения 20.11.2013).
Публикации с ключевыми словами: корреляция, дисперсионный анализ, регрессионная модель, т – статистика, F- статистика, коэффициент детерминации
Публикации со словами: корреляция, дисперсионный анализ, регрессионная модель, т – статистика, F- статистика, коэффициент детерминации
Смотри также:
- Дисперсионный анализ факторов при имитационном моделировании сложных систем
- Применение метода активного планирования эксперимента в задачах синтеза гасителей вибрации проводов воздушных систем энергоснабжения
- Прогнозирование шума автомобильных шин. Методики измерения шума и обработки экспериментальной информации
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



