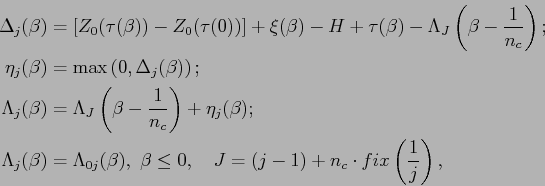О журнале
Редакционная политика
Редколлегия
Специальности
Авторам
Партнеры
Контакты







Архив

 
 
 
 
 
 
Приложение к журналу

 
 
 
 
 
 
Другие журналы

научное издание МГТУ им. Н.Э. Баумана

НАУКА и ОБРАЗОВАНИЕ

Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211.  ISSN 1994-0408

Влияние крутильных колебаний на процесс сверления с вибровозбудителем

#12 декабрь 2007

А.М. Гуськов, С.А. Воронов, А.С. Квашнин

Влияние крутильных колебаний на процесс сверления с вибровозбудителем

Особенностью сверления глубоких отверстий малого диаметра является затруднительное удаление стружки из зоны резания [1]. В случае резания с непрерывной (сливной) стружкой возможны повреждения и даже поломка инструмента. Математические модели, описывающие режимы процесса сверления, при которых образуется сливная стружка, встречаются во многих работах. Так в статье [2] была получена кинематическая модель, позволяющая описать процесс получения спиральной либо ленточной сливной стружки. Разработанная методика позволила прогнозировать среднюю длину элемента стружки. Вынос стружки существенно облегчается, если стружка получается сегментированной. Существуют различные методы дробления стружки [1,3]. Наиболее эффективным является вибрационное сверление, при котором суппорту сверла сообщаются осевые вибрации требуемой частоты и амплитуды. Тогда правильный подбор значений рабочей частоты и амплитуды вибратора позволяет получить дробленую стружку при осевых колебаниях инструмента.

В работе [4] был предложен метод авторезонансного сверления, основанный на явлении возникновения автоколебаний во время процесса обработки резанием. Разработанная методика требует детального изучения динамики инструмента и формирования стружки в процессе резания. Эти исследования были проведены в России около десяти лет назад, а построенные модели и некоторые результаты анализа по ним используются до сих пор, в том числе в работах [5,6,7]. Наибольшее внимание в большинстве работ по динамике вибросверления уделено моделированию осевых колебаний инструмента, так как именно осевые перемещения определяют формирование стружки, срезаемой режущими кромками. В действительности же инструмент в процессе обработки нагружен помимо продольной силы резания еще и крутящим моментом, из-за которого могут появляться и крутильные колебания.

Влияние крутильных колебаний на автоколебания при сверлении спиральными сверлами изучалось в работе [8]. Для исследования авторы использовали модель с двумя степенями свободы (крутильной и осевой). При этом модель не учитывала такие особенности процесса резания, как эффект «затирания» материала задней гранью инструмента, наличие трения между интсрументом и стружкой. В работе исследована обработка предварительно засверленного отверстия, но не учитывалось влияние на процесс обработки перемычки сверла между режущими кромками.

Статья [9] посвящена анализу возбуждения колебаний большой амплитуды кратных крутильной собственной частоте. Была разработана математическая модель, учитывающая совместные осевые и крутильные колебания инструмента. При этом помимо самих сил резания в динамической модели был учтен эффект затирания обрабатываемого материала задней гранью сверла, что, естественно, стало возможным благодаря подробному описанию в модели геометрии режущих кромок инструмента. Так же в данной работе учитывалось, отличное от всей остальной режущей кромки, поведение перемычки между кромками. В результате, при помощи построенной модели, авторам удалось описать процесс формирования не только дна получаемого отверстия, но и боковой поверхности, что позволяет оценить качество обработки детали: шероховатость получаемой поверхности отверстия и отклонение от круглости.

В статье [8] модель включает сосредоточенную осевую силу резания и сосредоточенный закручивающий момент резания, как силовые факторы, воздействующие на сверло со стороны обрабатываемого материала. Спиральное сверло здесь считалось естественно закрученным стержнем. Предполагалось, что крутящий момент резания, действующий против направления «закрученности» сверла, распрямляет его, при этом сверло естественным образом удлиняется в осевом направлении. Аналогичное представление для сил резания было в работе [14]. Исследования авторов подводили нас к тому, что в спиральных сверлах реализовывались помимо крутильных, еще и продольные колебания, дающие волнообразную поверхность дна получаемого отверстия. Возникновение подобной волнистой поверхности -- это результат действия регенеративного механизма в технологической системе. Из-за чего в процессе обработки материала могут возникать автоколебания инструмента в силу конечности его осевой и крутильной жестокостей.

Из анализа упомянутых выше работ можно сделать вывод, что динамика процесса резания не является результатом вынужденных колебаний от внешней нагрузки (сил резания), а представляет собой автоколебательный процесс, который может быть как устойчивым, так и неустойчивым. В работе [5] автор исследовал устойчивость продольных автоколебаний сверла при непрерывном резании; принималась полиномиальная (кубическая) зависимость осевой силы резания от толщины стружки. Области устойчивости процесса сверления для продольных колебаний инструмента были получены асимптотическим методом. Изучение было продолжено с включением в динамическую модель уравнений образования новых поверхностей в [7] и позднее в [15], что позволило смоделировать нестационарные режимы, включая моменты входа-выхода режущих кромок инструмента из обрабатываемого материала. Явление синхронизации осевых колебаний инструмента на частоте внешнего источника колебаний (вибратора) для случая вибросверления рассматривалось в работах [6,15]. Здесь же следует отметить, что в указанных работах [5,6,7,15] не учитывались крутильные колебания инструмента.

В публикации [17] процесс вибросверления моделировался как колебания системы с двумя степенями свободы (осевой и крутильной). Основные уравнения модели включали величины, описывающие геометрию режущих кромок. Так же как и в работе [15] модель описанная в статье [17] может быть использована как для непрерывного резания, так и для сверления с выходом инструмента из металла в процессе обработки заготовки. Целью работы [17] являлось компьютерное моделирование поверхности, получаемой при обработке, и сравнение результатов работы построенной модели с экспериментальными данными. Однако, в отличие от настоящей работы, в статье [17] в качестве независимой переменной при интегрировании полной системы уравнений выбиралось время, что при учете крутильных колебаний требует дополнительной интерполяции в ходе интегрирования. Таким образом в ходе интегрирования может появляться некоторая погрешность интерполирования.

В качестве итога следует отметить, что вопросу влияния крутильных колебаний на процесс сверления с вибровозбудителем посвящено относительно мало научных работ.

Постановка задачи. Разработке моделей процесса сверления посвящено много исследований, в которых изучались различные расчетные схемы упругой системы станок-приспособление-инструмент-деталь. Этому уделяется значительное внимание, поскольку принятие той или иной расчетной схемы, в конечном счете, определяет результаты исследования. На основе имеющихся данных об экспериментальных виброустройствах можно сделать вывод, что основным звеном, определяющим крутильную жесткость упругой системы и непосредственно связывающим инструмент, работающий в глубоком отверстии, со станком, является стебель сверла. Вследствие весьма большой длины и малого диаметра, стебель сверла является наименее жестким элементом всей технологической системы. При определенных условиях влияние крутильных колебаний на процесс образования стружки становится существенным. В связи с этим, в настоящей работе рассматривается динамика сверла как системы с двумя степенями свободы.

Колебательные движения режущих кромок инструмента, в сочетании с движениями, задаваемыми непосредственно вибровозбудителем, могут оказывать дополнительное влияние на процесс обработки материалов. Взаимодействие автоколебательной системы с внешними источниками возбуждения приводят к сложной динамике технологической системы. Основная задача данной работы -- исследование влияния крутильных колебаний инструмента, возникающих при выходе инструмента из материала в процессе вибросверления, на его осевые колебания.

Описание модели. Расчетная схема процесса вибрационного сверления с осевой податливостью крепления инструмента совместно с расчетной схемой инструмента представлена на рис. 1. В данном случае описание модели аналогично указанному в [18].

Рис. 1: Принципиальная схема процесса вибрационного сверления с осевой податливостью крепления инструмента
\includegraphics[width=12cm,keepaspectratio]{pictures/sxema-drilling.eps}

Предполагается, что деталь и инструмент являются недеформируемыми твердыми телами, податливым является только крепление инструмента. Рассматривается инструмент с $ n_c$ симметрично расположенными по торцу режущими кромками. Деталь вращается вокруг своей оси с постоянной угловой скоростью $ \omega$ и перемещается с постоянной скоростью осевой подачи $ V$ (рис. 1). 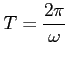Номинальная подача на оборот определяется как $ h_0=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}VT$ , где $ T=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}\dfrac{2\pi}{\omega}$ .

Модель инструмента представляется как система с осевой и крутильной степенями свободы (рис. 1). Здесь $ m,\Theta$  -- масса и физический момент инерции (приведенный к правому сечению упругого стержня, работающего на кручение) инструмента; $ w,\varphi$  -- осевое перемещение и угол закручивания правого сечения сверла. Инструмент и его крепление имеют конечные осевую и крутильную жесткости $ k_{ax}$ и $ k_{rot}$ . При этом вибратор задает движение левого сечения крепления инструмента по закону $ \tilde Z_0(t)=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}\tilde A_0\sin{(\omega_0t)}$ , где $ \tilde A_0$  -- амплитуда вибраций; $ \omega_0$  -- круговая частота задаваемых вибраций. При внедрении режущих кромок инструмента в материал заготовки в правом сечении стебля сверла возникают сосредоточенные осевая сила резания $ P_c$ и момент резания $ M_c$ . Рассеивание энергии колебаний как осевых, так и крутильных учитывается введением коэффициентов линейного вязкого демпфирования $ d_{ax},d_{rot}$ .

Модель сил резания. Для описания осевой силы резания $ P_c$ (рис. 1), действующей на режущую кромку сверла, воспользуемся следующим представлением [7], [15]:

$\displaystyle P_c =\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{} \left(k^0_c h_0\right)\bar\eta^q,$ (1)

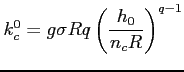где $ k^0_c =\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{} g\sigma R q \left(\dfrac{h_0}{n_c R}\right)^{q-1}$  -- статическая жесткость резания, зависящая от геометрии режущей кромки, материала обрабатываемой заготовки и диаметра сверла; $ q$  -- параметр нелинейности закона резания; $ \bar\eta$  -- приведенная толщина снимаемого слоя,

$\displaystyle \bar\eta =\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{} \left... ...box{\ensuremath{=}}}{}1}^n \left(n_c\cdot\eta_j\right)^q\right]^{\dfrac{1}{q}},$ (2)

где $ \eta_j$  -- безразмерная толщина материала заготовки, снимаемого $ j$  - ой режущей кромкой.

Закручивающий сверло момент $ M_c$ (рис. 1) определяется как произведение окружной силы резания $ P_t$ на некоторое плечо $ l_t$ , составляющее долю от радиуса получаемого отверстия (в общем случае $ 0<l_t\le{R}$ ). При этом само значение окружной силы резания пропорционально значению осевой силы резания. В итоге выражение для момента резания примет вид $ M_c=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}\mu_PP_c$ , где $ \mu_P$  -- постоянный коэффициент.

Модель инструмента. Для перехода к безразмерным величинам, отнесем все линейные размеры к $ h_0$ , в качестве масштаба времени возьмем время одного оборота детали $ T$ и введем обозначение $ \omega_0T=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}2\pi p$ , где $ p$  -- количество колебаний инструмента, сообщаемых вибратором, за время одного оборота детали. Для того, чтобы исключить переменное запаздываение, перейдем от независимой переменной безразмерного времени $ \tau$ к безразмерному полному углу поворота правого сечения сверла $ \beta$ (подробнее см. [18]). Тогда уравнения движения инструмента для принятой расчетной схемы без учета выхода инструмента из материала заготовки примут вид (штрихами здесь обозначены производные разных порядков по безразмерному углу поворота сечения $ \beta$ ):

\begin{equation*}\begin{aligned}\xi^{\prime\prime} &+ \left(2\zeta\left(2\pi f_{... ...tionary{}{\hbox{\ensuremath{=}}}{}1- \psi^{\prime}, \end{aligned}\end{equation*}

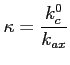где $ \kappa=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}\dfrac{k^0_c}{k_{ax}}$  - безразмерная жесткость резания; $ f_{ax},f_{rot}$  -- безразмерные собственные частоты осевых и крутильных колебаний инструмента; $ \zeta$  -- безразмерный коэффициент демпфирования; $ A_0$  -- безразмерная амплитуда вибратора; безразмерный коэффициент трения крутильных колебаний примем равеным $ \mu_\zeta\cdot\nobreak\discretionary{}{\hbox{\ensuremath{\cdot}}}{}2\zeta\left(2\pi f_{ax}\right)$ , где $ \mu_\zeta$  -- некоторый множитель.

Модель формирования поверхности. Вывод уравнений, описывающих процесс образования новых поверхностей [7,15] при сверлении, подробно описан в статье [18]. В безразмерном виде эти уравнения сводятся к системе нелинейных алгебраических уравнений, включающих функции с запаздывающим аргументом. Для сверления инструментом с $ n_c$ режущими кромками уравнения формирования новых поверхностей принимают вид:

\begin{equation*}\begin{aligned}\Delta_j(\beta) &=\nobreak\discretionary{}{\hbox... ...}}}{}(j-1)+n_c \cdot fix \left(\dfrac{1}{j}\right), \end{aligned}\end{equation*}

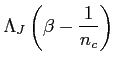где $ \Delta_j(\beta)$  -- безразмерное расстояние от $ j$  - ой режущей кромки до необработанной поверхности; $ H$  -- безразмерное расстояние от инструмента до средней поверхности торца детали в начальный момент времени; $ \Lambda_J\left(\beta - \dfrac{1}{n_c}\right)$  -- безразмерное отклонение поверхности торца от плоскости под 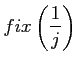$ j$  - ой режущей кромкой; $ \Lambda_j(\beta)$  -- поверхность, получаемая за счет снятия мгновенной толщины снимаемого слоя $ \eta_j(\beta)$ с поверхности, сформированной «предыдущей» режущей кромкой; $ fix \left(\dfrac{1}{j}\right)$  -- функция, дающая значение $ 1$ , в случае когда $ j=1$ , или 0 , когда $ j$  -- любое другое число.

Уранения (3), (4) формируют полную систему уравнений модели процесса вибросверления.

Сверление с вибровозбудителем. Подробное исследование устойчивости процесса резания без внешнего источника вибраций с непрерывной стружкой для системы с двумя степенями свободы приводится в работе [18].

Для объяснения особой эффективности применения внешних источников вибраций в технологических системах с конечной осевой жесткостью рассмотрим два следующих рисунка: рис. 2 -- отображение Пуанкаре и сечение стружки для одной из реализаций (при $ p=3$ ) для системы с абсолютно жестким креплением инструмента и для системы с конечной осевой жесткостью крепления инструмента. Из диаграмм рис. 2а видно, что толщина снимаемого слоя каждой режущей кромкой периодически зависит от частоты накладываемых вибраций $ p$ и для выбранного значения амплитуды возбуждения $ A_0=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}0,2$ в случае «жесткой» системы процесс резания происходит без фрагментации стружки.

Рис. 2: Влияние осевой жесткости крепления инструмента на форму стружки: а -- отображения Пуанкаре(($ \circ$ ) -- «жесткая» система, ($ \bullet$ ) -- «мягкая» система); б -- варианты формы сечения стружки для реализаций при $ p=3$ : сливная -- для «жесткой» системы и дискретная -- для «мягкой» системы
[а]\includegraphics[width=7cm,keepaspectratio]{pictures/eta_vibdril_rigid-Synxr.eps} [б]\includegraphics[width=7cm,keepaspectratio]{pictures/Lambda_vibdril_rigid-Synxr.eps}

При этом для системы с конечной осевой жесткостью крепления инструмента для того же диапазона значений частоты возбуждения $ p$ , что и для «жесткой» системы, но при амплитуде возбуждения гораздо меньшей $ A_0=0,05$ , происходит резание с дробленой стружкой, причем на всем интервале значений $ p$ , и с гораздо большим врезанием. Такое явление объясняется тем, что для «мягкой» системы имеет место так называемый эффект авторезонансного резания, когда значение рабочей частоты вибратора выбирается вблизи значения собственной частоты продольных колебаний. В итоге, для «мягкой» системы при существенно меньшей мощности источника вибраций (по сравнению с мощностью источника для «жесткой» системы) можно получить во-первых, дискретную стружку, а во-вторых, большую амплитуду колебаний инструмента, а следовательно, большую скорость обработки по сравнению с обработкой при «жесткой» системе.

Кроме задачи непосредственного дробления стружки, которая упрощается введением в модель системы адекватной конечной осевой жесткости, существует проблема сделать так, чтобы стружка была как можно более регулярной, а сам процесс дробления был устойчивым, т.е. необходимо, чтобы на протяжении всего времени обработки стружка дробилась на одинаковые между собой части (чего не наблюдается, например, для системы на рис. 2). Эффект регулярности дробленой стружки может быть достигнут, при изменении соотношения между $ \kappa$ и $ \kappa_{*}$ , т.е. при переходе из области «неустойчивости» (рис. 3а) в область устойчивого резания с непрерывной стружкой (рис. 3б), увеличив, например, значение параметра $ \zeta$ .

Рис. 3: Отображение Пуанкаре для приведенной толщины срезаемого слоя $ \bar\eta$ при различных значениях $ \kappa$ : a - при $ \zeta=0,02$ и б - при $ \zeta=0,05$
[]\includegraphics[width=7cm,keepaspectratio]{pictures/eta_kappa_z002.eps} []\includegraphics[width=7cm,keepaspectratio]{pictures/eta_kappa_z005.eps}
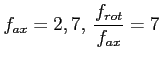(при получении диаграмм на рис. 3 принимались следующие значения параметров: $ f_{ax}=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}2,7,\: \dfrac{f_{rot}}{f_{ax}}=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}7$ ). Так на рис. 4

Рис. 4: Отображения Пуанкаре для толщины стружки $ \bar\eta$ от частоты внешнего источника $ p$ (а -- система с одной степенью свободы; б -- система с двумя степенями свободы), при $ \zeta=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}0,05 \left(\kappa<\kappa_{*}\right)$
[]\includegraphics[width=7cm,keepaspectratio]{pictures/eta_p.eps} []\includegraphics[width=7cm,keepaspectratio]{pictures/eta_p_f_rot_f_ax_5.eps}
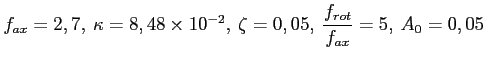показаны отображения Пуанкаре, полученные для систем с одной и двумя степенями свободы при следующих значениях параметров: $ f_{ax}=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}2,7,\: \kappa=\nobreak... ...ensuremath{=}}}{}5,\: A_0=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}0,05$ . Из диаграмм видно, что для выбранного значения $ \zeta$ в зоне синхронизации (рис. 4а при $ p\in\left[2,90;3,30\right]$ и рис. 4б при $ p\in\left[3,14;3,30\right]$ )могут быть получены реализации с регулярной дискретной стружкой. При этом диапазон значений $ p$ с такой стружкой для системы с двумя степенями свободы заметно уже (на рис. 4б стружка диапазона частоты вибратора $ p\in\left[3,33;3,10\right]$ не удовлетворяет условию регулярности).

Необходимость учета крутильной степени свободы так же проявляется, если построить отображения Пуанкаре, взяв при этом в качестве изменяемого параметра амплитуду вибратора $ A_0$ . Так диаграммы на рис. 5,6

Рис. 5: Отображения Пуанкаре для осевого перемещения $ \xi$ от амплитуды внешнего источника $ A_0$ (а -- система с одной степенью свободы; б -- система с двумя степенями свободы), при $ \zeta=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}0,02 \left(\kappa>\kapp... ...},\: \dfrac{f_{rot}}{f_{ax}}=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}5$
[]\includegraphics[width=7cm,keepaspectratio]{pictures/xi_A0_p_eqv_f_ax.eps} []\includegraphics[width=7cm,keepaspectratio]{pictures/xi_A0_f_rot_f_ax_5_z_002_p_eqv_f_ax.eps}

Рис. 6: Отображения Пуанкаре для толщины стружки $ \bar\eta$ от амплитуды внешнего источника $ A_0$ (а -- система с одной степенью свободы; б -- система с двумя степенями свободы), при $ \zeta=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}0,02 \left(\kappa>\kapp... ...},\: \dfrac{f_{rot}}{f_{ax}}=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}5$
[]\includegraphics[width=7cm,keepaspectratio]{pictures/eta_A0_p_eqv_f_ax.eps} []\includegraphics[width=7cm,keepaspectratio]{pictures/eta_A0_f_rot_f_ax_5_z_002_p_eqv_f_ax.eps}
получены для следующих значений параметров $ f_{ax}=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}2,7,\: \kappa=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}8,48\times10^{-2}$ , при этом рассмотрен случай когда трение выбрано так ( $ \zeta=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}0,02$ ), что система работает в неустойчивой области, т.е. при $ \kappa>\kappa_{*}$ . Влияние крутильных колебаний в данном случае также очевидно.

Результаты эксперимента. В системах, подобных рассматриваемой в данной работе, при некоторых значениях параметров, возможно появление автоколебаний. Если, например, менять относительную жесткость резания $ \kappa$ , то, построив диаграмму Пуанкаре в осях $ \left(Extr[\bar\eta],\kappa\right)$ (рис. 3), фактически можно получить бифуркационную диаграмму. При этом, как и говорилось ранее под устойчивым движением понимается резание с непрерывной стружкой постоянной толщины. Таким образом на рис. 3 показано влиянние трения в системе на устойчивость процесса резания. Для рис. 3а, например, при $ \kappa=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}8,48\times10^{-2}$ , имеет место случай $ \kappa>\kappa_{*}$ , для рис. 3б наоборот -- $ \kappa<\kappa_{*}$ .

Ниже приводится сравнение процесса авторезонасного сверления с данными, полученными численным интегрированием уравнений модели. В ходе эксперимента применялось двухкромочное сверло из быстрорежущей стали, с покрытием кромок TiN, тип заточки -- крест. Обрабатывалась заготовка из стали XC48 по французской классификации AFNOR. Параметры процесса сверления имели следующие значения: диаметр сверла -- $ d=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}2,3, $мм ; подача на оборот -- $ h_0=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}0,02, $мм/об ; частота вращения детали -- $ n=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}11000, $об/мин ; частота дискретизации сигнала $ 10000, $Гц . Значения параметров для численного интегрирования принимались: $ q=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}0,75,\: n_c=\nobreak\discre... ...{=}}}{}0,75,\: \kappa_{*}=\nobreak\discretionary{}{\hbox{\ensuremath{=}}}{}1,38$ .

Рис. 7: Реализация процесса в случае «мягкой» технологической системы (($ -$ ) -- численное моделирование, ($ \bullet$ ) -- эксперимент): а -- смещение инструмента $ \xi$ б -- толщина снимаемого слоя $ \eta$
[]\includegraphics[width=7cm,keepaspectratio]{pictures/sim-exp_xi_tau.eps} []\includegraphics[width=7cm,keepaspectratio]{pictures/sim-exp_eta_tau.eps}

Рис. 8: Сечение стружки в случае «мягкой» технологической системы: а -- эксперимент б -- численное интегрирование
[]\includegraphics[width=7cm,keepaspectratio]{pictures/exp_Lambda_tau.eps} []\includegraphics[width=7cm,keepaspectratio]{pictures/sim_Lambda_tau.eps}

Выводы. По результатам исследований в данной работе можно сделать ряд выводов:

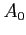  • использование внешних источников осевых колебаний особенно эффективно при определенных значениях частоты $ p$ и амплитуды $ A_0$ самого источника;
  • при моделировании процесса сверления с вибратором для систем с конечной осевой жесткостью при относительно небольших значениях отношениях парциальных частот 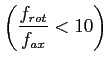$ \left(\dfrac{f_{rot}}{f_{ax}} < 10\right)$ необходимо учитывать крутильную степень свободы инструмента.

Дальнейшая работа над рассматриваемой проблемой предполагает так же следующие этапы:

  • исследование влияния меняющейся геометрии режущей кромки инструмента на динамику процесса вибросверления;
  • исследование влияния технологических параметров на процесс образования боковой поверхности отверстия с целью прогнозирования качества и точности обработки.

Работа выполнена благодаря финансовой поддержке РФФИ грант  07" 08" 00592.

Литература

1
Подураев В.Н. Обработка резанием с вибрациями. -- М.: Машиностроение, 1970. -- 352с.

2
F. Ke, J. Ni, Continious chip formation in drilling. -- International Journal of Machine Tools and Manufacture, Vol. 45, 2005. -- pp.1652-1658.

3
Stephenson D.A., J.S. Agapiou, Metal Cutting Theory and Practice. -- Marcel Decker, New York, 1997.

4
Подураев В.Н., Кибальченко А.В. Технология оборонной промышленности для производства изделий народного потребления. -- М.: Росконверсия, 1993. -- 528с.

5
Воронов С.А. Оптимизация процесса вибрационного сверления. -- Труды МВТУ. 332. Динамика и прочность машин, Москва. -- с.13-25.

6
A.M. Gouskov, S.A. Voronov, S.A. Butzer, Chatter Synchronization in Vibratory Drilling Dynamics. -- Acoustics and Simulations/ASME 2000, 68, 2000. -- pp.263-270.

7
S.A. Batzer, A.M. Gouskov, S.A. Voronov, Modeling vibratory drilling dynamics, Transactions of the ASME, Journal of Vibration and Acoustics, 123, 4, 2001. -- pp.435-443.

8
P.V. Bayly, S.A. Metzler, A.J. Shaut, S.G. Young, Theory of torsional chatter in twist drills: model, stability analysis and composition test. -- Journal of Manufacturing Science and Engineering, Vol. 123, 2002. -- pp.552-561.

9
P.V. Bayly, M.T. Lamar, S.G. Calvert, Low-frequency regenerative vibration and the formation of lobed holes in drilling. -- Journal of Manufacturing Science and Engineering, Vol. 124, May, 2002.

10
G.L. Cantero, M.M. Tardio, J.A. Canteli, M. Marcos, M.H. Miguelez, Dry drilling of alloy Ti-6Al-4V. -- International Journal of Machine Tools and Manufacture, Vol. 45, 2005. -- pp.1246-1255.

11
M. Pirtini, I. Lazoglu, Forces and hole quality in drilling. -- International Journal of Machine Tools and Manufacture, Vol. 45, 2005. -- pp.1271-1281.

12
R.F. Hamade, C.Y. Seif, F. Ismail, Extracting cutting force coefficients from drilling experiments. -- International Journal of Machine Tools and Manufacture, 2005. -- pp.1-10.

13
J.S. Strenkowski, C.C. Hsieh, A.J. Shih, An analitical finite element technique for predicting thrust force and torque in drilling. -- International Journal of Machine Tools and Manufacture, Vol. 44, 2004. -- pp.1413-1421.

14
S. Ema, H. Fujii, E. Marui, Whirling vibration in drilling. Part 3: Vibration analysis in drilling workpiece with a pilot hole. -- Transactions of the ASME, Journal of Engineering for Industry, Vol. 110, Nov., 1988. -- pp.315-321.

15
Гуськов А.М. Нелинейная динамика вибрационного сверления. Роль уравнений образования новых поверхностей. --Труды симпозиума CSDT-2000, СТАНКИН, 2000. -- с.93-101.

16
G. Stepan, Modelling nonlinear regenerative effects in metal cutting. -- Phil. Trans. R. Soc., 359, 2001. -- pp.739-757.

17
J.C. Roukema, Y. Altintas, Kinematic model of dynamic drilling process. -- Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Anaheim, 2004. -- pp.13-20.

18
Гуськов  А.М., Воронов С.А., Квашнин А.С. Влияние крутильных колебаний  на  процесс  вибросверления. -  Вестник  МГТУ им  Н.Э. Баумана. Серия Машиностроение. № 1, Москва, 2007. - с. 3-19.
 

This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

Публикации с ключевыми словами: сверление глубоких отверстий малого диаметра, режим сверления, дробление стружки, авторезонансное сверление
Публикации со словами: сверление глубоких отверстий малого диаметра, режим сверления, дробление стружки, авторезонансное сверление
Смотри также:
Тематические рубрики:
Поделиться:
 
ПОИСК
 
elibrary crossref ulrichsweb neicon rusycon
 
ЮБИЛЕИ
14 января 2017 год. Камышная Э.Н., доцент кафедры ИУ-4 МГТУ им. Н.Э.Баумана

29 января 2016 год Шахнов В.А., член-корреспондент РАН, д.т.н., профессор МГТУ им. Н.Э.Баумана

ФОТОРЕПОРТАЖИ
 
СОБЫТИЯ
Всероссийская олимпиада студентов «Я — профессионал» 2022

Юбилейный, V сезон всероссийской олимпиады студентов «Я – профессионал» запущен!

 
НОВОСТНАЯ ЛЕНТА
26.05.2022
Всероссийская олимпиада студентов «Я — профессионал»

15.06.2018
Искусcтвенный интеллект научит горожан экономить время

19.01.2017
На сайте ВАК размещена справочная информация об изданиях, входящих в международные реферативные базы данных и системы цитирования

4.01.2017
На сайте ВАК размещена обновленная информация, о перечне рецензируемых научных изданий

19.12.2016
В МГТУ им.Н.Э.Баумана состоялся региональный этап Всероссийского Конкурса «IT-Прорыв»




Авторы
Пресс-релизы
Библиотека
Конференции
Выставки
О проекте
Rambler's Top100
Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00)
  RSS
© 2003-2024 «Наука и образование»
Перепечатка материалов журнала без согласования с редакцией запрещена
 Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00)