научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#10 октябрь 2007
УДК. 534.222
Сальников Б.А., Петухов В.И., Сальникова Е.Н.,
Вагеник И.А., Сальников Н.Б., Минапов С.А.
Дальневосточный государственный технический университет
Введение
Одним из важнейших направлений современной акустики океана является мониторинг гидрофизических полей. Идея использования акустической томографии для изучения процессов, происходящих в океане, в последнее время получила активное развитие. В отличие от традиционных контактных способов, к достоинствам томографических методов можно отнести возможность исследования больших пространства водной среды в системе единого времени [1].
Однако, несмотря на множество разработанных теорий, применение томографических методов в реальных океанических экспериментах ограничивается целым рядом факторов. К ним относится: несовершенство аналитических методов расчёта акустических полей в случайно-неоднородном океане, не достаточно ясное понимание механизмов, влияющих на процессы формирования акустических полей, а также несовершенство методов обработки результатов экспериментов. Всё это приводит к расхождению теоретических расчётов и результатов обработки данных натурных экспериментов.
Для оптимальной постановки томографических экспериментов и адекватной интерпретации полученных данных необходимо учитывать влияние различных факторов, влияющих на процессы формирования зональной структуры зондирующих акустических полей в океанической среде.
К таким факторам относятся широкий спектр внутренних волн, синоптических вихрей и тонкоструктурные расслоения водной толщи [2]. Внутренние волны различных пространственно-временных масштабов играют доминирующую роль в мелкомасштабной изменчивости океана, передачи импульса, а также в перемешивании вод устойчиво-стратифицированного океана [3].
Именно перемешивание, возникающее при разрушениях внутренних волн, а также чисто кинематический эффект сжатия и растяжения слоёв воды в высших модах внутренних волн в немалой степени способствуют повсеместно наблюдаемому тонкоструктурному расслоению вод океана – океан оказался скорее дискретным, чем непрерывным образованием [2].
Ранее считалось, что в океане существует устойчивое распределение океанографических характеристик. Временная изменчивость считалась в основном незначительной и связывалась, главным образом, с сезонными и приливными колебаниями, а также с воздействием локальных метеоусловий на верхние слои океана. Поэтому предполагалось, что среднеклиматическое состояние вод океана, в отличие от атмосферы, мало зависит от конкретных условий и поэтому измеренные в каком-либо районе океана профили океанографических характеристик, например скорости звука, с точностью до сезонной изменчивости верхних слоёв океана можно уверено использовать для характеристики гидрологических условий в этом районе в любой другой момент времени. В настоящее время стало ясно, что прогноз гидролого-акустических данных или районирование океана по типам кривых вертикального разреза скорости звука (ВРСЗ), может оказаться недостаточным.
Впервые тонкоструктурное расслоение вод океана, влияние внутренних волн обсуждались на Первой школе-семинаре по акустике океана в 1982 году [4]. Влияние микроструктуры и тонкой структуры поля скорости звука подробно рассматриваются в [5]. Тонкая структура вод океана может иметь ступенчатый и случайный характер, причём уровень неоднородности в верхних перемешиваемых слоях на порядок выше, чем на больших глубинах [6,7].
Влияние микроструктуры поля скорости звука на различные гидроакустические явления, например предреверберацию, засветку зон тени, весьма многообразно. Эффект предреверберации [8] заключается в том, что перед приходом рефрагированных в волноводе сигналов наблюдается звуковой фон, нарастающий со временем и достигающий максимума в момент прихода фронта основного сигнала. Считается, что предреверберация возникает вследствие рассеяния звука в прямом направлении на неоднородностях водной среды или неровностях границ подводного звукового канала [9]. Засветка зон тени также объясняется частичным перераспределением звукового поля из-за взаимодействия с неоднородностями тонкой структуры [10-16]. Рассеяние звука на горизонтально протяжённых плоскослоистых тонкоструктурных неоднородностях относится к классу резко анизотропного рассеяния. Звуковая волна, идущая в прямом и зеркальном направлениях, попадая в зоны тени, приводит к их засветке, а попадая в зоны конвергенции - к предреверберации. Таким образом, предреверберация несёт полезную информацию о характеристиках рассеивателей и может быть использована как аппарат исследования пространственных неоднородностей водной среды в системах акустического мониторинга океана.
Для широкого внедрения томографических методов исследования океана необходимо более глубокое понимание процессов формирования зональной структуры акустических полей (ЗСАП) в случайно-неоднородных подводных волноводах (СНПВ). При разработке теорий и расчётных моделей необходим учёт всех факторов, влияющих на распределение ВРСЗ, т.к. даже небольшие флуктуации скорости звука приводят к заметным изменениям в структуре зондирующих полей. Кроме того, такие явления, как предреверберация и засветка зон тени, могут служить инструментом, характеризующим уровень стохастичности гидролого-акустических характеристик водной среды.
Разработка методов расчёта, учитывающих выше названные факторы, позволит создать достаточно адекватные модели для проведения имитационного моделирования распространения звуковых волн в СНПВ и выявить основные закономерности формирования ЗСАП.
В [17] предложен метод расчёта ЗСАП в СНПВ, основанный на численном решении с заданным шагом по дальности стохастического полевого уравнения лучевого распространения, полученного непосредственно из принципа Ферма. Для моделирования анизотропной стохастичности параметров водной среды вертикальная проекция модельного волновода разбивалась на прямоугольные ячейки, в центр которых генератором случайных чисел распределялись максимальные значения случайной компоненты поля скорости звука ΔC»(x,z), не превышающие наперёд заданные. Присвоенные в центрах ячеек значения ΔC»(x,z) снижались до нуля к их границам.
В данной статье приведены результаты численного эксперимента по классификации подводных волноводов в зависимости от уровня случайной компоненты поля скорости звука. Режимы стохастичности подводных волноводов определялись по типу деформаций функций вертикальных разрезов акустического поля (ВРАП) A(x,n) на дискретных дальностях x. За эталонные принимались ВРАП, рассчитанные для детерминированного ВРСЗ.
ИСХОДНЫЕ ДАННЫЕ ДЛЯ МОДЕЛИРОВАНИЯ
Исходные данные для моделирования: длина полигона – 120 км; глубина полигона - 2000м; ось подводного звукового канала располагается на глубине 1000 м, источник излучения - на глубине z0=300 метров. Вертикальная проекция модельного полигона разбита на ячейки размером 25х500 метров; случайная компонента поля скорости звука ΔC»(x,z) дискретно изменяется от 0,05 до 15,0 м/с. Для каждого значения ΔC»(x,z) проводилось по 1000 экспериментов. Угол раскрыва излучения соответствовал режиму однолучевого приёма для детерминированного ВРСЗ на дальностях, соответствующих границам между верхними и нижними зонами конвергенции. ЗСАП рассчитывалась с дискретностью 0,1° на вертикальных разрезах от 20 до 120 км с дискретностью по дальности 1 км, z=Dz×n, где z-вертикальная координата модельного волновода, Dz=50 м – интервал усреднения по глубине, n=1¸N=40 – номер дискретного отсчёта по глубине, N – количество дискретных отсчётов.![]() ЗСАП, соответствующая распространению лучей в детерминированном волноводе, изображена на рис.1. В правой части рисунка изображен вид функции детерминированной компоненты ВРСЗ.
ЗСАП, соответствующая распространению лучей в детерминированном волноводе, изображена на рис.1. В правой части рисунка изображен вид функции детерминированной компоненты ВРСЗ.
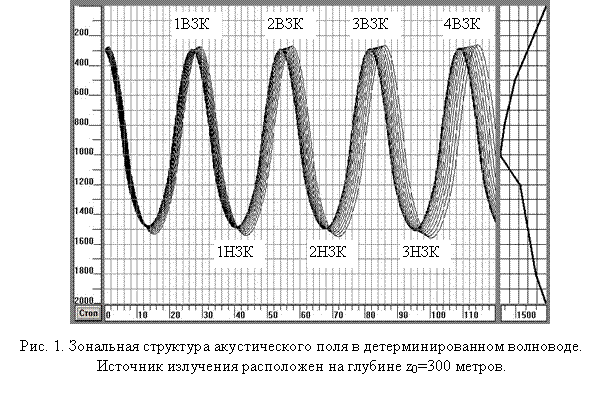 |
На рис.1 цифрами обозначены порядковые номера центров верхних и нижних зон конвергенции.
Координаты по дальности центров верхних и нижних зон конвергенции определялись по координатам максимумов нормы функции ВРАП, координаты границ между верхними и нижними зонами конвергенции - по координатам минимума нормы функции ВРАП (см. рис. 2). Координаты экстремумов нормы функции ВРАП на вертикальных разрезах определялись по формуле [17]
 .
.
Расчётная норма функции ВРАП пропорциональна мощности огибающей сигнала, снимаемого с вертикальной антенной решётки в реальном эксперименте.
|
|
|
Рис. 2. Зависимость нормы ВРАП от расстояния при различных уровнях случайной компоненты поля скорости звука |
Дальнейшие исследования ЗСАП проводились на дальностях соответствующих экстремумам нормы функции ВРАП. Координаты по дальности центров верхних зон конвергенции соответственно равны: x=28 км, 55 км,83 км, 110 км; центров нижних зон конвергенции – x=40 км, 68 км,96 км; границы между верхними и нижними зонами конвергенции – x=33 км, 60 км, 88км, 116 км (для лучей, идущих сверху вниз) и x=49 км, 77 км, 105 км (для лучей, идущих снизу вверх).
Результаты ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ
Результаты численного моделирования показали, что наибольшие искажения зональной структуры акустического поля происходят на дальностях, соответствующих координатам границ между верхними и нижними зонами конвергенции, наименьшие – на дальностях, соответствующих координатам центров зон конвергенции. С увеличением уровня случайной компоненты поля скорости звука изменяется вид функции ВРАП. По характеру изменения вида функций ВРАП возможно классифицировать режимы флуктуаций поля скорости звука в СНПВ. Наиболее чётко выделяются три режима – режим слабых флуктуаций, режим сильных флуктуаций и режим насыщения.
Информативными признаками режима слабых флуктуаций поля скорости звука являются снижение максимума функций ВРАП и расширение диапазона глубин прихода лучевых траекторий.
Информативными признаками режима сильных флуктуаций являются трансформация функций ВРАП из одномодальных в двумодальные, фокусировка и усиление поля на глубинах, "запрещённых" детерминированным ВРСЗ.
Информативными признаками режима насыщения является снижение двух максимумов функции ВРАП до равномерного распределения поля по всему диапазону глубин. Дискретные значения отсчётов ВРАП по глубине подводного волновода стремятся к величине 1/N, где N – количество дискретных отчётов.
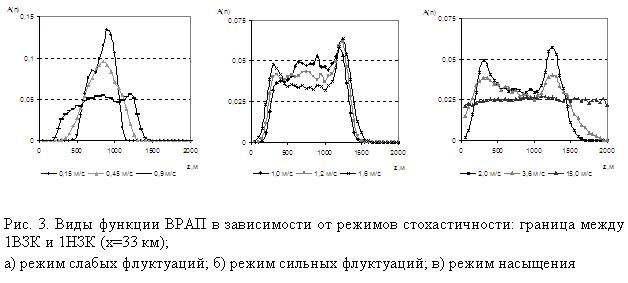
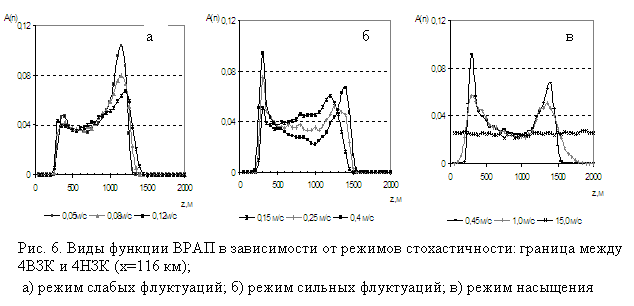
В зависимости от расстояния излучатель-приёмная система при одинаковых уровнях ΔC»(x,z) наблюдаются разные режимы флуктуаций поля скорости звука. Так, на границе 1ВЗК и 1НЗК при x=33 км режим слабых флуктуаций наблюдается до уровня ΔC»(x,z)=0,8 м/с; на границе 2ВЗК и 2НЗК (x=60 км) – до ΔC»(x,z)=0,35 м/с; на границе 3ВЗК и 3НЗК (x=88 км) – до ΔC»(x,z)=0,2м/с; на границе 4ВЗК и 4НЗК (x=116 км) – до ΔC»(x,z)=0,12 м/с (Рис.3 – 6).
 |
 | ||||
 | ||||
 | ||||
Исходя из анализа изменения функций ВРАП, была проведена классификация режимов флуктуаций поля скорости звука в случайно-неоднородном рефракционном подводном волноводе. Для границы между 1ВЗК и 1НЗК (х=33 км) были получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,8 м/с, режим сильных флуктуаций от 0,9 м/с до 1,6 м/с, при значениях ΔC»(x,z) больших 1,6 м/с наступает режим насыщенных флуктуаций.
На границе между 2ВЗК и 2НЗК (х=60 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,35 м/с, режим сильных флуктуаций от 0,4 м/с до 0,9 м/с, при значениях ΔC»(x,z) больших 0,9 м/с наступает режим насыщенных флуктуаций. На границе между 3ВЗК и 3НЗК (х=88 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,2 м/с, режим сильных флуктуаций от 0,25 м/с до 0,6 м/с, при значениях ΔC»(x,z) больших 0,6 м/с наступает режим насыщенных флуктуаций.
Для границы между 4ВЗК и 4НЗК (х=116 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,12 м/с, режим сильных флуктуаций от 0,13 м/с до 0,4 м/с, при значениях ΔC»(x,z) больших 0,4 м/с наступает режим насыщенных флуктуаций. Сводные результаты для границ зон конвергенций (лучи от поверхности ко дну) изображены на рис. 7.

Наиболее интересным физическим результатом влияния случайной компоненты поля скорости звука на процессы формирования структуры акустического поля является фокусировка и усиление звука с увеличением ΔC»(x,z) на глубинах, «запрещённых» детерминированным ВРСЗ. Этот эффект неоднократно наблюдался в натурных экспериментах и объяснялся ошибками в позиционировании судов и измерении ВРСЗ по трассе распространения зондирующих сигналов.
На рис.8. приведены зависимости изменения приповерхностных и придонных максимумов ВРАП для лучей, идущих от поверхности к дну, при увеличении уровня случайной компоненты поля скорости звука ΔC»(x,z). Как следует из приведённых зависимостей, функции достигают максимума при значениях ΔC»(x,z) соответствующих границе между режимом сильных флуктуаций и режимом насыщения.
 |
Общим информативным признаком изменения уровня ΔC»(x,z) для режимов слабых и сильных флуктуаций является увеличение уровня засветки зон тени (ЗЗТ). ЗЗТ определялась как сумма дискретных значений ВРАП, вышедших за диапазон глубин зоны акустической освещенности для детерминированного ВРСЗ. На рис.9-12 приведёны диаграммы величины ЗЗТ в % в зависимости от ΔC»(x,z) на дальностях х=33 км, 60 км, 88 км, 116 км для режимов слабых и сильных флуктуаций. Из представленных результатов следует, что, с ростом ΔC»(x,z) происходит увеличение ЗЗТ. Причём уровень ЗЗТ в область больших глубин для лучей идущих от поверхности к дну выше, чем в область меньших глубин.
Из представленных результатов следует (см. рис.11-12), что на дальностях после третьей зоны конвергенции суммарная ЗЗТ при равных значениях ΔC»(x,z) снижается: для 88 км при ΔC»(x,z)=0,15 м/с ЗЗТ тени составляет 12,9%, а для 116 км – 10,6 %. Это объясняется увеличением диапазона глубин прихода лучевых траекторий для детерминированного ВРСЗ с увеличением расстояния источник – приёмник. В режиме насыщения исследование ЗЗТ не имеет смысла, т.к. лучи стремятся равномерно распределиться по всему диапазону глубин волновода, ЗСАП разрушается.
 |
Ниже представлены результаты анализа структуры ВРАП для лучей, идущих от дна к поверхности на границах зон конвергенции для дальностей x=49км, 77км и 105км, что соответствует границам между 1НЗК и 2ВЗК, 2НЗК и 3ВЗК, 3НЗК и 4ВЗК, соответственно (см. рис. 13 – рис. 15).

Как следует из представленных результатов, для лучей, идущих от дна к поверхности, и лучей, идущих от поверхности к дну, информативные признаки искажений ВРАП при различных режимах флуктуаций поля скорости звука идентичны.
Основным отличием для лучей, идущих от дна к поверхности, является то, что фокусировка и усиление поля в режиме сильных флуктуаций происходит не на двух интервалах глубин, приповерхностном и придонном, а на одном – приповерхностном (см. рис. 16).
 |
Исходя из анализа вида деформаций функций ВРАП (см. рис.13 – 16) была проведена классификация режимов флуктуаций поля скорости звука в случайно-неоднородном рефракционном подводном волноводе для лучей, идущих от дна к поверхности.
Для границы между 1НЗК и 2ВЗК (х=49 км) были получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,5 м/с, режим сильных флуктуаций от 0,55 м/с до 1,2 м/с, при значениях ΔC»(x,z) больших 1,2 м/с наступает режим насыщенных флуктуаций.
На границе между 2НЗК и 3ВЗК (х=77 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,3 м/с, режим сильных флуктуаций от 0,35 м/с до 0,8 м/с, при значениях ΔC»(x,z) больших 0,8 м/с наступает режим насыщенных флуктуаций.
На границе между 3НЗК и 4ВЗК (х=105 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,15 м/с, режим сильных флуктуаций от 0,2 м/с до 0,4 м/с, при значениях ΔC»(x,z) больших 0,4 м/с наступает режим насыщенных флуктуаций. Сводные результаты для границ зон конвергенций (лучи идут от дна к поверхности) приведены на рис. 17.
 |
На рис.18-20 приведёны диаграммы величины ЗЗТ в зависимости от ΔC»(x,z) для разрезов на дальностях: х=49 км, 77 км, 105 км для режимов слабых и сильных флуктуаций. Видно, что с ростом ΔC»(x,z) также происходит увеличение ЗЗТ на границах зон конвергенции. Для лучей идущих от дна к поверхности основной является ЗЗТ в область меньших глубин (к поверхности).
 | |||||
 | |||||
 | |||||
С увеличением расстояния источник – приёмная система происходит эффект «накопления» влияния случайной компоненты поля скорости звука, с увеличением порядкового номера зоны конвергенции происходит снижение значения ΔC»(x,z) для соответствующих границ режимов стохастичности. В зависимости от порядкового номера зоны конвергенции (расстояние источник – приёмная система) режим стохастичности исследуемой акватории может быть различным.
Далее приведены результаты анализа искажений вида функций ВРАП в зависимости от уровня случайной компоненты поля скорости звука на дальностях, соответствующих центрам верхних и нижних зон конвергенции (см. рис. 21 –27). Координаты центров верхних зон конвергенции соответственно равны x=28 км, 55 км, 83 км,110 км, а нижних – x=40 км, 68 км, 96 км.

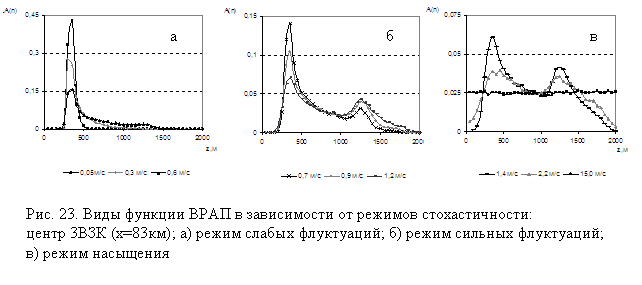
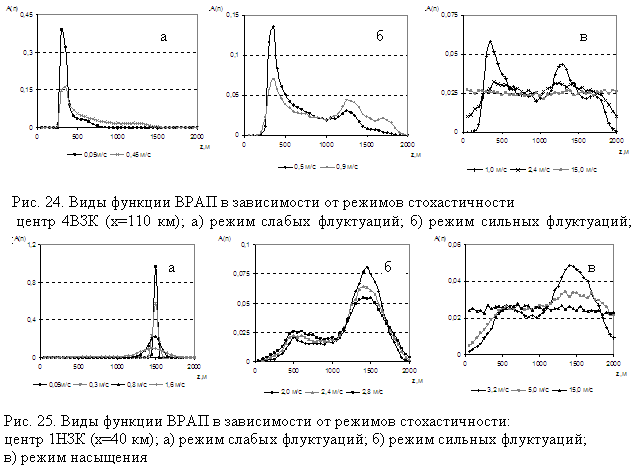

При режиме слабых флуктуаций (рис.21а-27а) наблюдается снижение максимума функции ВРАП и перераспределение поля: для верхних центров зон конвергенции - в область больших глубин; для нижних – к поверхности. Режим сильных флуктуаций характеризуется появлением дополнительного максимума (фокусировка поля) и его роста при увеличении значения ΔC»(x,z) (рис.21б-27б). Режим насыщения характеризуется стремлением функции ВРАП равномерно заполнить весь диапазон глубин (происходит разрушение ЗСАП) (рис.21в-27в).
Исходя из анализа вида деформаций функций ВРАП, была проведена классификация режимов флуктуаций поля скорости звука в случайно-неоднородном рефракционном подводном волноводе на дальностях, соответствующих координатам центров зон конвергенции.
В центре 1ВЗК (x=28 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 1,6 м/с, режим сильных флуктуаций до 3,2 м/с, при значениях ΔC»(x,z) больших, 3,2 м/с наступает режим насыщенных флуктуаций. В центре 2ВЗК (x=55 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,9 м/с, режим сильных флуктуаций до 2,2 м/с, при значениях ΔC»(x,z), больших 2,2 м/с, наступает режим насыщенных флуктуаций. Для центра 3ВЗК (x=83 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,6 м/с, режим сильных флуктуаций до 1,2 м/с, при значениях ΔC»(x,z), больших 1,2 м/с, наступает режим насыщенных флуктуаций. В центре 4ВЗК (x=110 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,4 м/с, режим сильных флуктуаций до 0,9 м/с, при значениях ΔC»(x,z), больших 0,9 м/с, наступает режим насыщенных флуктуаций.
В центре 1НЗК (x=40 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 1,6 м/с, режим сильных флуктуаций до 2,8 м/с, при больших значениях ΔC»(x,z) наступает режим насыщенных флуктуаций. В центре 2НЗК (x=68 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,8 м/с, режим сильных флуктуаций до 2,2 м/с, при ΔC»(x,z) выше 2,2 м/с наступает режим насыщенных флуктуаций. В центре третьей НЗК (x=96 км) получены следующие результаты: режим слабых флуктуаций – до значения ΔC»(x,z) = 0,45 м/с, режим сильных флуктуаций до 1,2 м/с, при значениях ΔC»(x,z) более 1,2 м/с наступает режим насыщенных флуктуаций.
Сводные результаты для значений ΔC»(x,z), соответствующих границам режимов стохастичности на дальностях центров зон конвергенции, приведены на рис. 28.
 |
Из приведённых результатов следует, что с увеличением порядкового номера зон конвергенции также наблюдается эффект «накопления» влияния случайной компоненты поля скорости звука. С увеличением порядкового номера центров верхних зон конвергенции значения ΔC»(x,z), соответствующие границам режимов, снижаются с 1,6 м/с до 0,4 м/с – для слабых флуктуаций, с 3,2 м/с до 0,9 м/с – для режима сильных флуктуаций (рис.28а). Для центров нижних зон конвергенции значения ΔC»(x,z), соответствующие границам режимов стохастичности снижаются с 1,6 м/с до 0,45 м/с – для слабых флуктуаций, с 2,8 м/с до 1,2 м/с – для режима сильных флуктуаций (рис.28б).
ЗЗТ с ростом уровня ΔC»(x,z) увеличивается на всех исследуемых разрезах. Для центров верхних зон конвергенции основной является ЗЗТ в область больших глубин (рис.29). Для центров нижних зон конвергенции основной является ЗЗТ в область меньших глубин (рис.30), во всех случаях ЗЗТ возрастает с увеличением уровня ΔC»(x,z).
 | |
 |
На рис. 31 приведена сводка результатов численного моделирования по определению границ режима слабых флуктуаций поля скорости звука на дальностях экстремумов нормы функции ВРАП.
 |
ВЫВОДЫ
1. Результаты численных экспериментов по моделированию дальнего распространения акустических сигналов показывают, что существует принципиальная возможность классификации подводных волноводов по уровню случайной компоненты поля скорости звука.
2. На процесс формирования зональной структуры акустических полей в случайно-неоднородных подводных волноводах, в основном, влияют два конкурирующих механизма, обусловленные рефракцией и стохастичностью термодинамических параметров водной среды. Максимальные изменения в зональной структуре акустического поля происходят на дальностях, соответствующих координатам границ между верхними и нижними зонами конвергенции, где механизм стохастичности проявляется в наибольшей степени, а минимальные – на дальностях, соответствующих координатам центров зон конвергенции.
3. Изложенный в данной статье подход по оценке функций ВРАП может быть реализован на основе обобщения данных натурных акустических экспериментов, что позволяет районировать акватории по уровню стохастичности термодинамических параметров водной среды вдоль трассы распространения звука.
ЗАКЛЮЧЕНИЕ
Предложенный в данной работе метод классификации подводных волноводов по уровню случайной компоненты поля скорости звука может быть использован при выборе оптимальных мест расположения рубежных систем охраны акваторий от несанкционированного проникновения подводных технических средств.
Работа выполнена в Дальневосточном государственном техническом университете в рамках целевой программы "Развитие научного потенциала высшей школы (2006-2008 годы)" по проекту: Интегрированный научно-образовательный центр ДВГТУ "Проблемы исследования и освоения ресурсов Мирового океана".
Литература
- Гончаров В.В., Куртепов В.М., Успехи и проблемы акустической томографии океана/ Акустические волны в океане. М: Наука 1987. с.15-24.
- Сабинин К.Д. Волновая изменчивость океана/ Акустические волны в океане. М.: Наука 1987. с.3-15
- Тернер Д. Эффекты плавучести в жидкостях. М.: Мир, 1977.
- Сабинин К.Д. Внутренние волны в океане/ Акустика океана: современное состояние. М.: Наука,1982. с.209-226
- Швачко Р.Ф. Флюктуации звука на неоднородностях толщи океана/ Акустика океана: современное состояние. М.: Наука, 1982. с.132-141.
- Фёдоров К.Н. Тонкая термохалинная структура вод океана. Л.: Гидрометеоиздат, 1976.
- Гостев В.С., Швачко Р.Ф. О микроструктуре температурного поля в океане/ Изв. АН СССР. Физика атмосферы и океана,1969, т.7, №5, с.1066-1074.
- Студеничник Н.В. Явление предреверберации в подводном звуковом канале/ IX всесоюзная акустическая конференция. Секция Д. М.: АКИН, 1977. с.45-48.
- Гостев В.С., Швачко Р.Ф. Предреверберация в океане с тонкоструктурной стратификацией/ Акустика океана. Сборник трудов школы-семинара акад. Л.М. Бреховских. – М.:Геос, 1998
- Бреховских Л.М., Лысанов Ю.П., Студеничник Н.В. К теории предреверберации звука в океане/ Докл. АН СССР. 1975. т. 239. №1. с.211-213.
- Гостев В.С., Носова Л.Н., Швачко Р.Ф. Исследование звукового поля взрывного сигнала в зонах геометрической тени глубокого океана/ Акуст. журн. 1998. т.44. №2. с.201-205.
- Гостев В.С., Носова Л.Н., Швачко Р.Ф. О некоторых возможностях акустической диагностики тонкоструктурных неоднородностей в океане/ Акуст. журн. 1998. т.44. №6. с.844-847.
- Гостев В.С., Швачко Р.Ф. Способы расчёта пространственно-временных и угловых характеристик звукового поля в зонах тени/ Акуст. журн. 1998. т.44. №2. с.274-277.
- Буренков С.В., Гостев В.С., Князева Н.И., Наумов С.С., Швачко Р.Ф. Исследование тонкой временной и угловой структуры звукового поля в зоне тени методом спектрометрии временных задержек/ Акуст. журн. 1998. т.44. №2. с.336-338.
- Швачко Р.Ф. Влияние фронтальной зоны на изменение структуры звукового поля/ Акуст. журн. 1998. т.44. №6. с.837-843.
- Гостев В.С., Швачко Р.Ф. Некоторые кинематические модели объёмной предреверберации в глубоком океане/ Акуст. журн. 1998. т.44. №6. с.857-860
- Сальников Б.А., Петухов В.И., Сальникова Е.Н., Вагеник И.А., Сальников Н.Б. Метод численного моделирования распространения звука в случайно-неоднородных подводных волноводах // Электронный Интернет-журнал "Наука и образование. Инженерное образование". 2007. №8. http://technomag.edu.ru:8001/db/msg/82620.html
Публикации с ключевыми словами: акустическое поле, подводные волноводы
Публикации со словами: акустическое поле, подводные волноводы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||




