научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#10 октябрь 2007
Крылов К.А., Мурзаханов Г.Х., Щугорев В. Н.
Московский энергетический институт (Технический университет), Россия.
Одним из факторов, ограничивающих использование современных композитных материалов, является их чувствительность к технологическим и эксплуатационным дефектам. В ходе эксплуатации конструкций из таких материалов возможно появление дефектов (непроклеев, расслоений и т.п.) или накопление рассеянных повреждений, приводящее к снижению прочностных характеристик [1...4]. Ударные взаимодействия со сторонними телами ускоряют появление и развитие этих дефектов [5], что может привести к ухудшению функциональных качеств или разрушению конструкции в целом [1, 6, 7]. Отсутствие экспериментальных исследований процессов разрушения и оценке характеристик трещиностойкости при динамическом нагружении сдерживает разработку норм дефектности конструкций из композитов.
Цель данной работы - оценка удельной работы межслойного разрушения композитов при динамическом нагружении, реализуемом по схеме нормального отрыва .Для моделирования динамического нагружения использована экспериментальная установка, схема которой показана на рисунке1. Двухслойный клееный образец из полиметилметакрилата (ПММА) с инициированной трещиной закреплялся в захват испытательной машины. Затем проводилось нагружение падающим грузом, приводящее к росту межслойной трещины.
Под удельной работой разрушения g понимаем работу Аg, необходимую для образования новой поверхности трещины DS: g = Ag / DS. Для реальных композитных материалов удельная работа разрушения g при квазистатическом нагружении имеет значение, находящееся в широком диапазоне от 102 до 103 Дж/м2. Для проведения экспериментального исследования была подготовлена партия клееных образцов из полиметилметакрилата (ПММА) (см. рисунок1). В качестве основы использовался брусок с размерами a*b*c – длина, ширина и высота соответственно, к которому приклеивался тонкий монослой с размерами a*b*h -длина, ширина и толщина слоя, числовые значения приведены в таблице.1 и 2. Для приклеивания слоя к нижней поверхности (большей грани) параллелепипеда использовался компаунд, приготовленный следующим образом. Десять частей эпоксидиановой ЭД-20 смолы смешивались с одной частью отвердителя ПЭПА. На склеиваемые поверхности предварительно при помощи наждачной бумаги наносились риски, затем поверхности обезжиривались для обеспечения лучшей адгезии слоя и монолита. Клей наносился как на поверхность параллелепипеда, так и монослоя. Отверждение происходило при комнатной температуре в течение 24 часов. Толщина клеевой прослойки не превышала 0,1 мм.
|
|
|
|
Схема нагружения |
|
|
а) |
б) |
|
Рис.1 |
|
В процессе подготовки образцов к испытаниям в клеевом слое образца инициировалось на длину ls начальное отслоение (рисунок 1.а). Для испытания образец консольно закреплялся в специально подготовленный захват, установленный на подвижной траверсе испытательной разрывной машины Р-5. К левому краю монослоя на тонкой стальной струне длиной L крепился груз массой m. Для используемых в эксперименте параметров системы -полоса-струна – масса – можно считать струну невесомой и абсолютно жесткой. Перед испытанием масса крепилась таким образом, чтобы деформация полосы отсутствовала. Это положение массы принималось за уровень нулевого потенциала. Нагружение проводилось следующим образом. Масса m поднималась на высоту H относительно нулевого уровня и затем отпускалась. Высота H выбиралась как нижняя граница от уровня запасенной энергии, приводящего к страгиванию трещины. Положение равновесия после нагружения показано на рисунке 1,б. При этом масса m заняла положение, задаваемое прогибом полосы f под действием массы, а длина трещины возросла от значения ls до значения le.
Таким образом, потенциальная энергия, запасенная массой в начальный момент времени: UH=m g H, где g=9,81м/с2, затратилась на приращение площади трещины DS, накопление потенциальной энергии в изогнутой полосе: Ub, рассеяние энергии в процессе колебаний полосы A и изменение потенциальной энергии массы Uf=m g f , где f прогиб полосы. Диссипацию энергии A будем считать сопоставимой с Ub. Баланс энергии до и после нагружения запишем в виде
UH = Ub + A – Uf + gdyn DS.
Полагая, что скорость движения трещины практически постоянна (за исключением моментов старта и остановки), получим выражение для удельной работы межслойного разрушения трещины
gdyn=(UH + Uf – Ub – A) / DS.
Экспериментальные результаты представлены в таблице 1 для груза массой 2,6 г и в таблице 2 - для груза массой 10,5 г. Здесь V=(2gH)0,5 -скорость приложения нагрузки, g-ускорение свободного падения, H-высота падения (рисунок 1), J-момент инерции отслоения.
Таблица 1 Обработка экспериментальных данных (масса 2,6 г)
|
№ испытания |
E, Па |
a, м |
b, м |
h, м |
J, м4 |
m, кг |
H, м |
ls, м |
le, м |
|
1 |
4,00E+09 |
0,0999 |
0,0511 |
0,001 |
4,26E-12 |
0,0026 |
0,66 |
0,025 |
0,031 |
|
2 |
4,00E+09 |
0,0999 |
0,0511 |
0,001 |
4,26E-12 |
0,0026 |
0,76 |
0,031 |
0,035 |
|
3 |
4,00E+09 |
0,0999 |
0,0511 |
0,001 |
4,26E-12 |
0,0026 |
0,96 |
0,035 |
0,04 |
|
4 |
4,00E+09 |
0,0999 |
0,0511 |
0,001 |
4,26E-12 |
0,0026 |
1,16 |
0,04 |
0,045 |
|
5 |
4,00E+09 |
0,0999 |
0,0511 |
0.0 |
0.0 |
0,0026 |
0.0 |
0.0 |
0,045 |
Продолжение таблицы 1
|
№ испытания. |
dl, м |
f, м |
Ub, Дж |
Pstat, Н |
U рез, Дж |
Ds, м 2 |
gdyn, Дж/м2 |
v, м/с |
gdyn/gstat |
|
1 |
0,006 |
1,49E-05 |
1,89E-07 |
0.0 |
1,68E-02 |
0,000307 |
54,8 |
3,59 |
8,76 |
|
2 |
0,004 |
2,14E-05 |
2,73E-07 |
0.0 |
1,94E-02 |
0,000205 |
94,7 |
3,86 |
15,1 |
|
3 |
0,005 |
3,19E-05 |
4,07E-07 |
0.0 |
2,45E-02 |
0,000256 |
95,7 |
4,33 |
15,3 |
|
4 |
0,005 |
4,54E-05 |
5,79E-07 |
0.0 |
2,96E-02 |
0,000256 |
115,0 |
4,77 |
18,4 |
|
5 |
0.0 |
0,008 |
0.0 |
1,2 |
0.0 |
0.0 |
gstat=6,25 |
0.0 |
0.0 |
Таблица 2 Обработка экспериментальных данных (масса 10,5 г)
|
№ испытания. |
E, Па |
a, м |
b, м |
h, м |
J, м4 |
m, кг |
H, м |
ls, м |
le, м |
|
1 |
4,00E+09 |
0,1004 |
0,0414 |
0,001 |
3,45E-12 |
0,0105 |
0,1 |
0,004 |
0,02 |
|
2 |
4,00E+09 |
0,1004 |
0,0414 |
0,001 |
3,45E-12 |
0,0105 |
0,12 |
0,02 |
0,036 |
|
3 |
4,00E+09 |
0,1004 |
0,0414 |
0,001 |
3,45E-12 |
0,0105 |
0,2 |
0,036 |
0,052 |
|
4 |
4,00E+09 |
0,1004 |
0,0414 |
0,001 |
3,45E-12 |
0,0105 |
0,25 |
0,052 |
0,067 |
|
5 |
4,00E+09 |
0,1004 |
0,0414 |
0,001 |
3,45E-12 |
0,0105 |
0,3 |
0,067 |
0,084 |
|
6 |
4,00E+09 |
0,0999 |
0,0511 |
0.0 |
0.0 |
0,0105 |
0.0 |
0,05 |
0.0 |
Продолжение таблицы 2
|
№ испытания |
Dl, м |
f, м |
U b, Дж |
Pstat, Н |
U рез, Дж |
Ds, м 2 |
gdyn ,Дж/м2 |
v, м/с |
gdyn/g stat |
|
1 |
0,016 |
1,99E-05 |
1,03E-06 |
0.0 |
1,03E-02 |
0,000662 |
15,5 |
1,40 |
2,41 |
|
2 |
0,016 |
1,16E-04 |
5,98E-06 |
0.0 |
1,24E-02 |
0,000662 |
18,6 |
1,53 |
2,89 |
|
3 |
0,016 |
3,50E-04 |
1,80E-05 |
0.0 |
2,06E-02 |
0,000662 |
31,1 |
1,98 |
4,82 |
|
4 |
0,015 |
7,48E-04 |
3,85E-05 |
0.0 |
2,58E-02 |
0,000621 |
41,5 |
2,21 |
6,43 |
|
5 |
0,017 |
1,47E-03 |
7,59E-05 |
0.0 |
3,10E-02 |
0,000704 |
44,0 |
2,42 |
6,8257 |
|
6 |
0.0 |
0,01 |
0.0 |
1,1 |
0.0 |
0.0 |
gstat =6,45 |
0.0 |
0.0 |
|
|
|
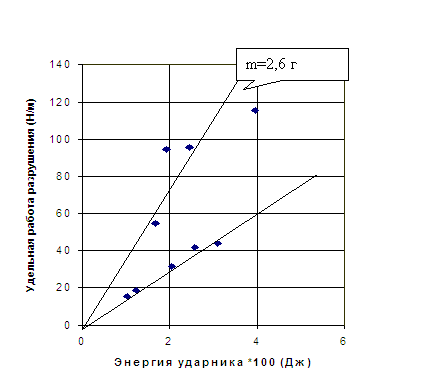
Удельная работа разрушения в зависимости от энергии ударника |
|
Рис.2 |
Последней строкой в таблицах показаны выборочные результаты статических испытаний. Коэффициент вариации при таких испытаниях [2] не превышает 15 %. Как показано в таблице 1 и 2 динамическая работа разрушения превышает статическое значение и значительно зависит от скорости приложения нагрузки, массы груза и энергии, накоп ленной к моменту контакта. Таким образом, при динамическом нагружении работа разрушения является функцией скорости и энергии падающей массы
|
|
|
Зависимость удельной работы разрушения от скорости контакта |
|
Рис.3 |
gdyn=gstat* F(m, v, U),
где F – поправочная функция, которую в первом приближении можно оценить, например, статистическими средствами пакета MS EXCEL (см врезку к рисунку 3).
На рисунке 2 представлена зависимость работы разрушения от энергии падающего груза в момент контакта. Рассмотрены два случая: груз массой 2,6 г и 10,5 г. Для одной и той же энергии, накопленной ударниками, нагружение меньшей массой приводит к более высокому значению работы разрушения, что коррелирует со скоростью ударника к моменту нагружения. В первом приближении зависимость работы разрушения от энергии ударника можно считать практически линейной. Причем это справедливо как для малой, так и для большой массы (рисунок 2).
Зависимость работы разрушения от скорости нагружения представлена на рисунке 3. Статическое значение работы разрушения соответствует нулевой скорости. Правее следует блок результатов для массы ударника 10,5 г, еще выше - блок результатов для массы 2,6 г. Для ударника меньшей массы работа разрушения выше (см. рисунок 2). При этом следует отметить, что для каждой изображенной точки графика энергия ударника разная.
|
|
|
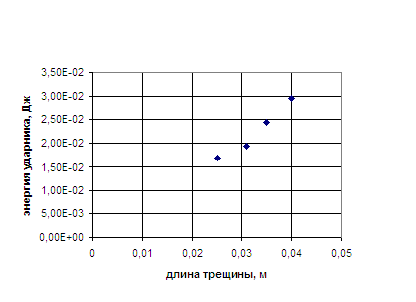
Энергия, необходимая для страгивания трещины (масса 2,6 гр.) |
|
Рис.4 |
|
. |
|
Энергия, необходимая для страгивания трещины (масса10,2 гр.) |
|
Рис.5 |
Как видно (рисунок 3- врезка), экспериментальные данные допустимо аппроксимируются квадратичной зависимостью с использованием статистических средств математического пакета MS EXCEL. По всей видимости, в допустимом интервале (низкоскоростное нагружение) результаты для больших масс ударника будут располагаться в зоне меньших скоростей.
На рисунке 4 и.5 представлены пороговые значения энергии, необходимые для страгивания трещины. Рисунок 4 соответствует массе 2,6 г, рисунок 5 - массе 10,5 г. Чтобы стронуть трещину - ударнику меньшей массы необходимо накопить большую энергию, чем ударнику большей массы
В результате проведенного исследования на модельных клееных образцах получено, что удельная работа межслойного разрушения при динамическом нагружении выше, чем при статическом. При постоянной энергии, накопленной ударником, менее массивные ударники приводят к более высокому значению работы разрушения, например (см рисунок 2) для UH,=0,02 Дж массе m=10,5 г соответствует gdyn =30н/м, массе m=2,6 г - gdyn = 70н/м. Таким образом, при столкновении с телами разной массы, имеющими равную накопленную энергию, более опасны тела с большей массой, так как для них удельная работа межслойного разрушения меньше и приближается к квазистатическому значению.
Литература
1. Болотин В. В. Дефекты типа расслоений в конструкциях из композитных материалов // Механика композит, материалов. — 1984. — № 2. — С. 239... 255.
2. Болотин В. В. Межслойное разрушение композитов при комбинированном нагружении // Механика композит, материалов. — 1988. — № 3. — С. 410... 418.
3. Болотин В.В. О динамическом распространении трещин // Прикл. математика и механика. –1992. –Т.56, вып. 1.-с. 150-162.
4. Болотин В.В., Щугорев В.Н. Влияние низкоскоростных ударов на остаточную прочность композитов. – 1993.Механика композитных материалов-Т.29, № 4 – с. 478-487.
5. Mursakhanov G. H., Shchugorev V.N. Destruction of dynamically loaded layered composite beams containing delaminations /Int. J. Eng. Dynamics, Strength, Wear – Resistance Machines.-1997.- Vol. 3. –P.2-11.
6. Грещук Л. Б. Разрушение композитных материалов при ударах с малыми скоростями // Динамика удара. — М., 1985. — С. 8 ... 46.
7. Майборода В. П., Кравчук А. С., Холин Н. Н. Скоростное деформирование конструкционных материалов. — М., 1986. — 264 с.
8. Рос С. С. Jr., Illg W., Carber D. P. Hidden impact damage in thick composites // Rev. of Progress in Quantitative Nondestructive Evaluation. Vol. 5. В. — N Y-: London, 1986. — P. 1215... 1226.
9. Lal К. М. Residual strength assessment of low velocity impact damage of graphite-epoxy laminates // J. of Reinforce Plast. Composite. — 1983. — Vol. 2, N 10. — P. 226... 238.
10. Joshi S. P., Sun C. T. Impact induced fracture in a laminated composite // J of Composite Materials. — 1985. — Vol. 19, N 1. — P. 51... 66.
11. Крылов К. А., Щугорев В.Н. Расчетно-экспериментальное исследование роста эллипсоидального отслоения в слоистых пластинах при динамическом нагружении. // Материалы ХII международного симпозиума «Динамические и технологические проблемы механики конструкций и сплошных сред».Тезисы докладов.- Москва.- МАИ.- 2006г. С 198.
12. Мурзаханов Г.Х., Щугорев В.Н. Разрушение композитов при низкоскоростном ударном нагружении. Ракетно-космическая техника. Фундаментальные и прикладные проблемы механики. Материалы международной научной конференции посвященной 90-летию В И Феодосьева. М. МГТУ 2006 г. С.60.
Публикации с ключевыми словами: композитные материалы, дефекты
Публикации со словами: композитные материалы, дефекты
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||