научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2013
DOI: 10.7463/1213.0676328
УДК 681.2.001.5
Россия, МГТУ им. Н.Э. Баумана
Статья посвящена доказательству правомерности замены при компьютерном моделировании конфигурации вектора напряженности электромагнитного поля витка произвольной формы, запитанного переменным током, на картину поля, полученную от того же витка, запитанного постоянным током.
Теория расчета накладных параметрических вихретоковых преобразователей достаточно сложна и хорошо разработана только для простых случаев витка преобразователя круглой формы и объекта измерений в виде бесконечного проводящего полупространства[1, 2]. При взаимодействии с объектами малого размера, по сравнению с преобразователем, эти расчеты провести не удается. Приходится проводить физическое моделирование при выборе формы и размера преобразователя. Физическое моделирование осложняется еще и тем, что простая круглая катушка чаще всего не удовлетворяет исследователя по показателям чувствительности преобразователя. Поэтому приходится тратить много времени и средств на подбор и изготовление различных вариантов преобразователей, прежде чем удается выбрать подходящий.
Расчет напряженности электромагнитного поля катушек произвольной формы возможен только компьютерными средствами из-за большой сложности. В работах [8, 9, 11] были предложены методы расчета компонентов вектора напряженности электромагнитного поля преобразователя произвольной формы, где он собирается из участков дуг и прямых разной протяженности и радиуса. Был создан программный пакет MagneticFiled 1.0., позволяющий собрать виток любой формы и по кусочкам, используя метод суперпозиции, рассчитать параметры электромагнитного поля[10].
При компьютерном моделировании использовался расчет поля витка, запитанного постоянным током. Могут возникнуть сомнения по поводу правомерности распространения этого метода моделирования для получения картины электромагнитного поля преобразователя, запитанного переменным током высокой частоты. Поскольку вихретоковые преобразователи работают только на переменном токе, возникает необходимость исследования влияния частоты питающего напряжения на конфигурацию электромагнитного поля преобразователя произвольной формы в свободном пространстве, что и является целью данной работы.
При создании различных измерительных приборов, оснащенных накладными параметрическими вихретоковыми преобразователями, достаточно часто возникает необходимость проектирования первичного преобразователя, что называется «под объект контроля» [2]. Для уменьшения доли физического моделирования предложен метод компьютерной визуализации полей вихретокового преобразователя (ВТП) произвольной формы. Компьютерная визуализация картины магнитного поля позволяет оценить особенности распределения вектора напряженности в пространстве при различных конфигурациях обмоток преобразователей, подобрать наиболее подходящие конструкции, оценить краевые эффекты и, в итоге, быстрее, легче и дешевле найти желаемое решение [3]. При вычислении распределения компонентов вектора напряженности электромагнитного поля нами использовался закон Био-Савара, который справедлив для магнитных полей постоянного тока [4, 8, 9]. Покажем правомерность использования его при моделировании компонентов вектора напряженности переменного магнитного поля витка, находящегося в свободном пространстве [5].
Напряженность магнитного поля описывается уравнением [6]

где ![]() вектор напряженности переменного магнитного поля, А/м;
вектор напряженности переменного магнитного поля, А/м; ![]() удельная электрическая проводимость, Сим/м;
удельная электрическая проводимость, Сим/м; ![]() магнитная проницаемость среды, Гн/м;
магнитная проницаемость среды, Гн/м;![]() диэлектрическая проницаемость среды, Ф/м;
диэлектрическая проницаемость среды, Ф/м; ![]() время, с.
время, с.
Среда, в которой поле взаимодействует с объектом контроля, - воздух. Тогда имеем
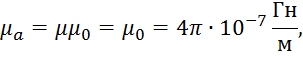
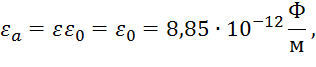
где 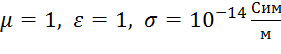 .
.
С учетом естественной поляризации получаем
![]() .
.
Вторым членом уравнения (1) можно пренебречь, без заметной потери точности моделирования. Уравнение в этом случае примет вид
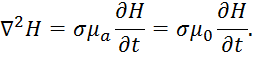
В случае гармонического электромагнитного поля
![]()
или в виде волнового уравнения:
![]()
![]()
Уравнение (2) представляет собой однородное уравнение Гельмгольца [4].
Поле ВТП образуется при питании преобразователя от генератора, работающего на частотах менее 10 МГц, в воздушной среде. Оценим величину К2:
![]()
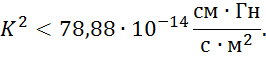
Этим значением также можно пренебречь. Тогда уравнение Гельмгольца превращается в уравнение Лапласа (частный случай уравнения Гельмгольца) и напряженность магнитного поля зависит только от пространственных координат и не зависит от времени (а, соответственно, от частоты).

![]()
Для подтверждения теоретических выводов были проведены физический и компьютерный эксперименты. При моделировании выбран накладной вихретоковый преобразователь квадратной формы восьмеркообразной намотки (рис. 1). Его геометрические характеристики: 96х96 мм, размеры обмотки 84х84 мм, обмотка состоит из двух секций по 30 витков, намотанных согласно проводом ПЭВ Ø 0,27 мм. Электрические параметры преобразователя: собственная индуктивность L=387 мкГн, активное сопротивление R=3,77 Ом.

Рис. 1. Накладной вихретоковый преобразователь квадратной формы восьмеркообразной намотки
Измерения напряженности магнитного поля проводились измерительным зондом, в качестве которого использована катушка индуктивности бескаркасной намотки наружным диаметром 3,5 мм, выполненная проводом ПЭВ Ø 0,1 мм, имеющая 28 витков. Электрические параметры зонда: L=1,2 мкГн, R=0,55 Ом. В ходе эксперимента измерялась ЭДС, наведенная переменным магнитным полем вихретокового преобразователя в измерительном зонде, при перемещении зонда вдоль и поперек катушки по сетке с шагом 5 мм. Вихретоковый преобразователь запитывался от генератора переменным напряжением с амплитудой 13 В и частотами 500 кГц, 1 МГц и 2 МГц. Данные измерений сведены в таблицу, созданную в среде MSExcel. По результатам измерений наведенной ЭДС рассчитан модуль вектора напряженности магнитного поля и построены 3D графики (рис. 2 - 4).
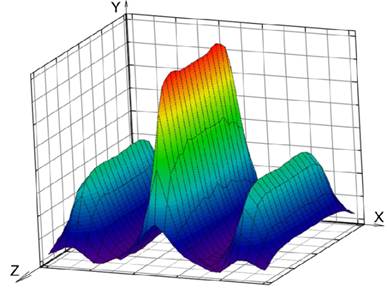
Рис. 2. График модуля вектора напряженности электромагнитного поля ВТП при частоте f=500 кГц

Рис. 3. График модуля вектора напряженности электромагнитного поля ВТП при частоте f=1000 кГц
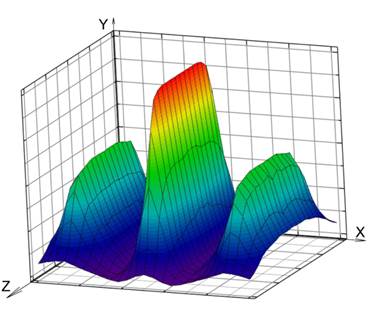
Рис. 4. График модуля вектора напряженности электромагнитного поля ВТП при частоте f=2000 кГц
Из сравнения графиков видна идентичность картины поля при разных частотах питающего генератора.
Затем по этим же геометрическим параметрам, в программной среде MagneticField 0.1, смоделирован виток ВТП и проведено компьютерное построение картины поля витка (Рис. 5) [9].
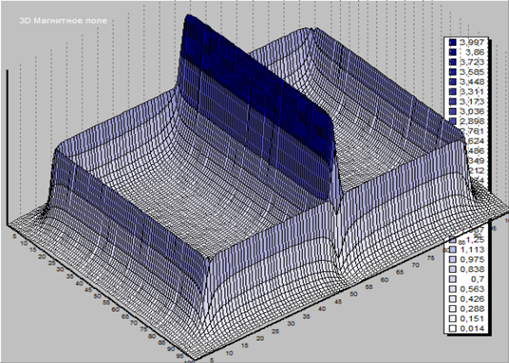
Рис. 5. Компьютерное моделирование электромагнитного поля накладного квадратного ВТП восьмеркообразной намотки
Для сравнения полученных результатов рассмотрим сечение картины поля, параллельное оси Х и проходящее через ось симметрии преобразователя. Получим график распределения модуля вектора напряженности в этом сечении [11]. Аналогичные сечения сделаны на 3D картинах полей, построенных в ходе физических экспериментов (рис. 6).
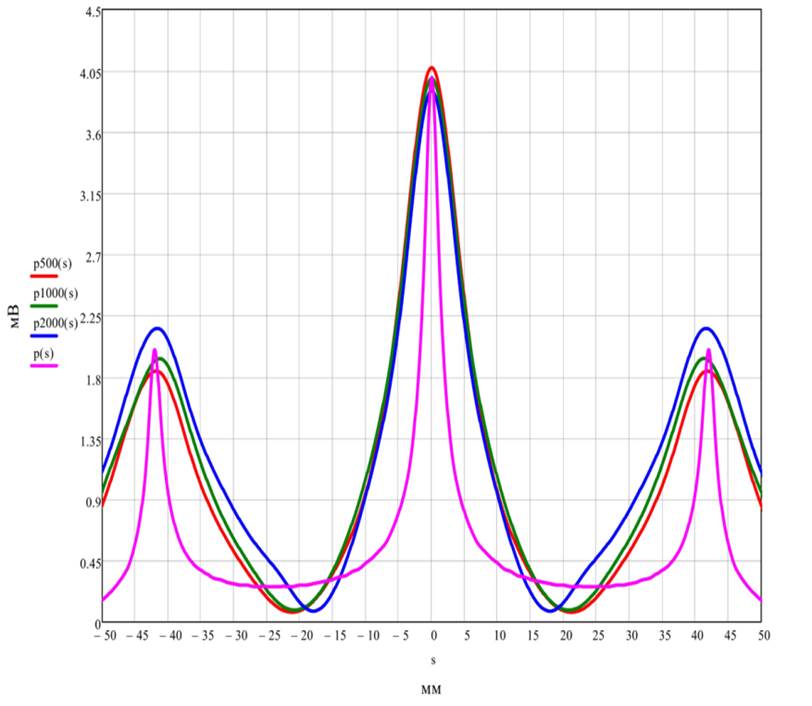
p500(s) – частота эксперимента 500 кГц; p1000(s) – частота эксперимента 1000 кГц; p2000(s) – частота эксперимента 2000 кГц; p(s) – результаты компьютерного моделирования
Рис. 6. Серединные сечения всех графиков и теоретическая кривая
На графике разными цветами дано распределение модуля вектора напряженности магнитного поля для физического эксперимента на разных частотах и для компьютерного моделирования. При анализе результатов получено практически полное совпадение графиков - расхождение по пиковым значениям менее 3%.
Таким образом, в результате теоретических и экспериментальных исследований показано отсутствие влияния частоты переменного магнитного поля ВТП на величину модуля вектора напряженности магнитного поля в пределах рабочих частот вихретоковых преобразователей и подтверждена правомерность использования закона Био-Савара при компьютерном моделировании картины распределения модуля вектора напряженности магнитного поля накладного ВТП произвольной формы в свободном пространстве. Все это дает возможность исследовать картину распределения вектора напряженности электромагнитного поля вихретоковых преобразователей любой геометрии.
Список литературы
1. Неразрушающий контроль: Справочник. В 7 т. Т. 2 / Под общ. ред. В.В. Клюева. М.: Машиностроение, 2003. 688 с.
2. Соболев В.С., Шкарлет Ю.М. Накладные и экранные датчики. Новосибирск: Наука, 1967. 144 с.
3. Веников В.А. Теория подобия и моделирования (применительно к задачам электроэнергетики): учеб. пособие для вузов. 2-е изд., доп. и перераб. М.: Высшая школа, 1976. 479 с.
4. Петренко Е.О. Электромагнитное поле накладного параметрического вихретокового преобразователя произвольной формы в свободном пространстве // Контроль. Диагностика. 2012. № 10. С. 72-75.
5. Арбузов Е.В., Петренко Е.О. Компьютерный синтез накладного вихретокового преобразователя // Сборник трудов 9-й Международной конференции «Эффективные методы автоматизации подготовки и планирования производства». Москва, МГТУ им. Н.Э. Баумана, 2012. С. 7-11.
6. Фейман Р., Лейтон Р., Сэндс М. Феймановские лекции по физике. Вып. 6: пер. с англ. М.: Мир, 1966. 345 с.
7. Говорков В.А. Электрические и магнитные поля. 3-е изд., перераб. и доп. М.:Энергия, 1968. 488 с.
8. Мушкаров А.С., Петренко Е.О. Машинная математическая модель электромагнитного поля вихретокового преобразователя сложной формы // Тезисы 2-й Всероссийской научной internet-конференции «Компьютерное и математическое моделирование в естественных и технических науках». Тамбов, ТГУ. 2001. С. 31-33.
9. Запускалов В.Г., Мушкаров А.С., Петренко Е.О. Исследование электромагнитного поля вихретокового преобразователя сложной формы с применением математической модели // Тезисы 3-й Международной научной конференции «Компьютерные методы и обратные задачи в неразрушающем контроле и диагностике». Москва, РОНКТД, 2002. С. 109-110.
10. Мушкаров А.С., Петренко Е.О. Создание математической машинно-ориентированной модели электромагнитного поля накладного вихретокового преобразователя // Тезисы 8-й Международной научно-технической конференции студентов и аспирантов «Радиоэлектроника, электротехника и энергетика». Москва, МЭИ, 2002. С. 401-402.
11. Арбузов Е.В., Петренко Е.О. Компьютерное моделирование электромагнитного поля вихретокового преобразователя произвольной формы // Материалы Международной конференции «Вычислительная математика, дифференциальные уравнения, информационные технологии». Улан-Удэ, ВСГТУ, 2009. С. 39-44.
Публикации с ключевыми словами: электромагнитное поле, электромагнитный метод, вихретоковый преобразователь
Публикации со словами: электромагнитное поле, электромагнитный метод, вихретоковый преобразователь
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



