научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#8 август 2007
DOI: 10.7463/0807.0067392
Постановка задачи многокритериальной оптимизации
УДК 519.6
Карпенко А.П., Федорук В.Г., Федорук Е.В.
1. Введение
Схема решения достаточно широкого класса вычислительных задач (далее – F-задач) неформально может быть представлена в следующем виде: область решения задачи покрывается некоторой сеткой; в узлах сетки производятся вычисления значений функций, ассоциированных с этими узлами; на основе вычисленных значений формируется решение задачи. В виде такой схемы может быть представлено, например, решение задачи глобальной условной оптимизации комбинацией метода случайного поиска с каким-либо методом локальной оптимизации, построение некоторыми методами множества Парето в задаче многокритериальной оптимизации и пр. Непосредственным стимулом для написания данной работы явилась проблематика организации параллельных вычислений при решении задач многокритериальной оптимизации.
Принципиальными являются следующие обстоятельства: 1)для вычисления значений функций, ассоциированных с узлами сетки, используется одна и та же программа; 2)для работы этой программы необходима информация только о тех узлах, которые она обрабатывает; 3)вычислительные сложности указанных функций являются случайными величинами с неизвестными статистическими характеристиками, т.е. вычислительные сложности непредсказуемо различны в различных узлах сетки; 4)формирование решения всей задачи выполняется на основе значений функций, ассоциированных с узлами сетки.
В случае, когда суммарная вычислительная сложность указанных функций велика, целесообразно решение F-задач на многопроцессорных вычислительных системах (МВС) с общей или распределенной памятью.
При решении задачи на МВС принято выделять следующие основные этапы [1]: декомпозиция (partitioning) – разбиение задачи на минимальные независимые подзадачи; коммуникации (communication) – определение информационных связей подзадач; кластеризация (agglomeration) – объединение подзадач в группы подзадач с целью минимизации информационных связей между ними; отображение (mapping) – назначение групп подзадач конкретным процессорам. Для F-задач этапы декомпозиции и коммуникации не представляют труда – подзадачи естественным образом ставятся в соответствие узлам сетки, а коммуникации между подзадачами отсутствуют. Этап кластеризации в данном случае вырожден, поскольку коммуникации между подзадачами отсутствуют и объединение подзадач в группы целесообразно выполнять, исходя только из потребностей этапа отображения. Таким образом, для F-задач основной является проблема оптимального отображения узлов сетки на параллельную вычислительную систему.
Отметим, что проблема оптимального отображения вычислительного процесса на параллельную вычислительную систему является одной из основных проблем, связанных с распараллеливанием вычислений. Хорошо известно, что эта проблема является NP-сложной и точные методы ее решения существуют для очень узкого класса задач [2].
На первый взгляд, F-задачи вкладываются в более широкий класс задач, в котором программы, обрабатывающие различные узлы сетки, информационно связаны. К задачам этого класса относятся, например, задачи математической физики, решаемые различными конечно-разностными и конечно-элементными методами. Вследствие исключительной практической важности таких задач, имеется большое количество работ, посвященных их распараллеливанию (см., например, [3]). Однако в задачах указанного класса полностью неизвестными являются вычислительные сложности функций, ассоциированных с узлами сетки, только на первой итерации. На последующих итерациях в качестве оценок вычислительных сложностей узлов можно использовать их значения на предыдущей итерации. Такая возможность отсутствует в F-задачах.
С другой стороны, при построении операционных систем МВС одной из важнейших является задача планирования вычислений при выполнении множества информационно и логически не связанных заданий. Этой проблеме также посвящено большое количество публикаций (см., например, [4]). Однако в F-задачах формирование решения всей задачи и, быть может, построение сетки, информационно и логически связаны с функциями, ассоциированными с узлами сетки. Поэтому прямое использование методов планирования вычислений, используемых в операционных системах МВС, в F-задачах не удается.
Чаще всего для приближенного решения задачи оптимального отображения используется метод балансировки загрузки МВС (loadbalancing). Основная идея метода состоит в распределении вычислений по процессорам таким образом, чтобы суммарная вычислительная и коммуникационная загрузки процессоров были примерно одинаковы. При этом не учитываются коммуникационные загрузки процессоров, обусловленные транзитными обменами и конфликты при обменах вследствие перегрузки коммуникационной сети [5].
Различают статическую и динамическую балансировку загрузки. Статическая балансировка загрузки выполняется однажды, до начала вычислений. Обзор методов статической балансировки загрузки применительно к параллельному решению задач математической физики дан, например, в работе [6].
Поскольку в F-задаче вычислительные сложности функций, ассоциированных с различными узлами расчетной сетки, различны и априори неизвестны, то статическая балансировка загрузки может быть неэффективной. В этом случае в процессе вычислений приходится перераспределять узлы расчетной сетки между процессорами системы - использовать динамическую балансировку загрузки. Обзор методов динамической балансировки загрузки приведен, например, в работе [7].
Методы динамической балансировки загрузки можно классифицировать, прежде всего, по следующим признакам: когда процессоры обмениваются информацией о своей текущей загрузке; где принимается решение о перераспределении загрузки; когда производится перераспределение загрузки; в соответствии с каким алгоритмом происходит перераспределение загрузки.
Процессоры могут обмениваться информацией о своей текущей загрузке периодически или когда загрузка процессора станет меньше некоторой допустимой, по появлении свободного процессора, по отторжении процесса процессором вследствие перегрузки и т.д. Решение о перераспределении загрузки может приниматься централизованно (на основе глобальной информации о загрузке) и децентрализовано (на основе только локальной информации о загрузке). Перераспределение загрузки может происходить синхронно и асинхронно. В качестве алгоритмов перераспределения загрузки могут использоваться детерминированные и стохастические алгоритмы, перераспределение загрузки может производиться по инициативе получателя и по инициативе отправителя, и пр.
В работе рассматриваются следующие методы балансировки загрузки:
1) статическая балансировка;
2) динамическая централизованная балансировка методом равномерной декомпозиции узлов - равномерная балансировка;
3) динамическая централизованная балансировка методом экспоненциальной декомпозиции узлов - экспоненциальная балансировка;
4) динамическая децентрализованная балансировка диффузным методом, в котором перераспределение загрузки производится по инициативе получателя - диффузная балансировка.
В последнем случае рассматривается перераспределение загрузки только по инициативе получателя, поскольку для F-задачи такой алгоритм более эффективен, чем перераспределение загрузки по инициативе отправителя. При этом возможно использование детерминированных и стохастических алгоритмов поиска отправителя. С точки зрения используемой в работе методики оценки эффективности балансировки эти алгоритмы эквивалентны. Поэтому алгоритм поиска отправителя в работе не фиксируется.
2. Постановка F-задачи
Пусть ![]() - n-мерный вектор параметров задачи. Полажим, что
- n-мерный вектор параметров задачи. Полажим, что ![]() , где
, где ![]() - n-мерное арифметическое пространство. Наряду со словами «вектор X», будем говорить «точка X». Параллелепипедом допустимых значений вектора параметров назовем не пустой параллелепипед
- n-мерное арифметическое пространство. Наряду со словами «вектор X», будем говорить «точка X». Параллелепипедом допустимых значений вектора параметров назовем не пустой параллелепипед ![]() , где
, где ![]() - заданные константы. На вектор X дополнительно наложено некоторое количество функциональных ограничений, формирующих множество
- заданные константы. На вектор X дополнительно наложено некоторое количество функциональных ограничений, формирующих множество ![]() , где
, где ![]() - непрерывные ограничивающие функции.
- непрерывные ограничивающие функции.
На множестве ![]() тем или иным способом (аналитически или алгоритмически) определена вектор-функция
тем или иным способом (аналитически или алгоритмически) определена вектор-функция ![]() . Ставится задача поиска значения некоторого функционала.
. Ставится задача поиска значения некоторого функционала.
Приближенное решение поставленной F-задачи, полагается, может быть найдено по следующей схеме.
Шаг 1. Покрываем параллелепипед П некоторой сеткой ![]() (равномерной или неравномерной, детерминированной или случайной) с узлами
(равномерной или неравномерной, детерминированной или случайной) с узлами ![]() .
.
Шаг 2. В тех узлах сетки ![]() , которые принадлежат множеству
, которые принадлежат множеству ![]() , вычисляем значения вектор функции
, вычисляем значения вектор функции ![]() .
.
Шаг 3. На основе вычисленных значений вектор функции ![]() находим приближенное значение функционала
находим приближенное значение функционала ![]() .
.
Суммарное количество арифметических операций, необходимых для однократного определения принадлежности вектора X множеству ![]() (т.е. суммарную вычислительную сложность ограничений
(т.е. суммарную вычислительную сложность ограничений ![]() и ограничивающих функций
и ограничивающих функций ![]() ), обозначим
), обозначим ![]() . Вообще говоря, величина
. Вообще говоря, величина ![]() зависит от вектора X. Мы, однако, пренебрежем этой зависимостью и будем полагать, что имеет место равенство
зависит от вектора X. Мы, однако, пренебрежем этой зависимостью и будем полагать, что имеет место равенство ![]() . Заметим, что до начала вычислений величина
. Заметим, что до начала вычислений величина ![]() , как правило, неизвестна. Однако в процессе первого же определения принадлежности некоторого узла сетки
, как правило, неизвестна. Однако в процессе первого же определения принадлежности некоторого узла сетки ![]() множеству
множеству ![]() , эту величину можно легко определить (с учетом предположения о независимости этой величины от вектора X). Поэтому будем полагать величину
, эту величину можно легко определить (с учетом предположения о независимости этой величины от вектора X). Поэтому будем полагать величину ![]() известной.
известной.
Неизвестную вычислительную сложность вектор-функции ![]() обозначим
обозначим ![]() . Подчеркнем зависимость величины
. Подчеркнем зависимость величины ![]() от вектора X. Величина
от вектора X. Величина ![]() удовлетворяет, во-первых, очевидному ограничению
удовлетворяет, во-первых, очевидному ограничению ![]() . Во-вторых, положим, что известно ограничение сверху на эту величину
. Во-вторых, положим, что известно ограничение сверху на эту величину ![]() , имеющее смысл ограничения на максимально допустимое время вычисления значения
, имеющее смысл ограничения на максимально допустимое время вычисления значения ![]() . Если значения этой вектор-функции вычисляются с помощью некоторого итерационного процесса, то такое ограничение обычно вводится для того, чтобы избежать «зацикливания» программы. Вычислительную сложность
. Если значения этой вектор-функции вычисляются с помощью некоторого итерационного процесса, то такое ограничение обычно вводится для того, чтобы избежать «зацикливания» программы. Вычислительную сложность ![]() назовем вычислительной сложностью узла
назовем вычислительной сложностью узла ![]() .
.
Вычислительную сложность конечномерной аппроксимации функционала ![]() положим равной
положим равной ![]() , а вычислительную сложность генерации сетки
, а вычислительную сложность генерации сетки ![]() - равной
- равной ![]() , где при данных
, где при данных ![]() величины
величины ![]() - известные константы.
- известные константы.
В качестве вычислительной системы рассмотрим однородную МВС с распределенной памятью, состоящую из процессоров ![]() и host-процессора, имеющих следующие параметры:
и host-процессора, имеющих следующие параметры: ![]() – время выполнения одной арифметической операции с плавающей запятой;
– время выполнения одной арифметической операции с плавающей запятой; ![]() - диаметр коммуникационной сети; l – длина вещественного числа в байтах;
- диаметр коммуникационной сети; l – длина вещественного числа в байтах; ![]() – латентность коммуникационной сети;
– латентность коммуникационной сети; ![]() [с] – время передачи байта данных между двумя соседними процессорами системы без учета времени
[с] – время передачи байта данных между двумя соседними процессорами системы без учета времени ![]() . Для простоты записи положим, что количество узлов сетки
. Для простоты записи положим, что количество узлов сетки ![]() кратно количеству процессоров в системе N, так что
кратно количеству процессоров в системе N, так что ![]() >1.
>1.
В качестве меры эффективности параллельных вычислений используем ускорение ![]() , где
, где ![]() - время последовательного решения задачи на одном процессоре системы,
- время последовательного решения задачи на одном процессоре системы, ![]() - время параллельного решения той же задачи на N процессорах,
- время параллельного решения той же задачи на N процессорах, ![]() - номер метода балансировки. Кроме того, для оценки эффективности балансировки используем следующие величины: оценка ускорения сверху
- номер метода балансировки. Кроме того, для оценки эффективности балансировки используем следующие величины: оценка ускорения сверху ![]() ; оценка ускорения снизу
; оценка ускорения снизу ![]() ; относительная оценка ускорения сверху
; относительная оценка ускорения сверху ![]() и аналогичная относительная оценка ускорения снизу
и аналогичная относительная оценка ускорения снизу ![]() .
.
Оценка ускорения сверху ![]() достигается в ситуации, когда вычислительные сложности
достигается в ситуации, когда вычислительные сложности ![]() всех узлов сетки
всех узлов сетки ![]() одинаковы и равны
одинаковы и равны ![]() . В этом случае легко обеспечить равномерную загрузку всех процессоров, что и является основанием для использования достигнутого ускорения в качестве оценки ускорения сверху. Данная ситуация моделирует случай, когда вычислительная сложность
. В этом случае легко обеспечить равномерную загрузку всех процессоров, что и является основанием для использования достигнутого ускорения в качестве оценки ускорения сверху. Данная ситуация моделирует случай, когда вычислительная сложность ![]() является случайной величиной с малой дисперсией.
является случайной величиной с малой дисперсией.
Оценка ускорения снизу ![]() достигается в ситуации, когда вычислительная сложность
достигается в ситуации, когда вычислительная сложность ![]() одного из узлов
одного из узлов ![]() сетки
сетки ![]() , многократно превышает вычислительные сложности
, многократно превышает вычислительные сложности ![]() любых других узлов этой сетки, т.е.
любых других узлов этой сетки, т.е. ![]() для любых
для любых ![]() ,
, ![]() . В этих условиях неизбежна сильная несбалансированность загрузки процессоров. В пределе при
. В этих условиях неизбежна сильная несбалансированность загрузки процессоров. В пределе при ![]() все процессоры, кроме процессора
все процессоры, кроме процессора ![]() , которому назначен для обработки узел
, которому назначен для обработки узел ![]() , по сути, простаивают в течение всего времени решения задачи и
, по сути, простаивают в течение всего времени решения задачи и ![]() . Это обстоятельство и является основанием для использования в данном случае достигнутого ускорения в качестве оценки ускорения снизу. Ситуация, близкая к данной, может иметь место в случае, когда дисперсия вычислительной сложности
. Это обстоятельство и является основанием для использования в данном случае достигнутого ускорения в качестве оценки ускорения снизу. Ситуация, близкая к данной, может иметь место в случае, когда дисперсия вычислительной сложности ![]() велика, а также когда объем множества
велика, а также когда объем множества ![]() значительно меньше объема параллелепипеда П.
значительно меньше объема параллелепипеда П.
Основные результаты в работе получены для случая, когда множество ![]() совпадает со всем параллелепипедом П, т.е. когда
совпадает со всем параллелепипедом П, т.е. когда ![]() . Это допущение не является слишком ограничительным, поскольку не принадлежность некоторого узла
. Это допущение не является слишком ограничительным, поскольку не принадлежность некоторого узла ![]() множеству
множеству ![]() можно интерпретировать как равенство нулю вычислительной сложности этого узла
можно интерпретировать как равенство нулю вычислительной сложности этого узла ![]() , что включает в себя ограничение
, что включает в себя ограничение ![]() .
.
Все графики в работе получены в системе MATLABпри следующих «тестовых» значениях параметров F-задачи и МВС: ![]() ;
; ![]() ; l=8;
; l=8; ![]() ;
;![]() ;
; ![]() ,
, ![]() , где
, где ![]() - ближайшее целое большее
- ближайшее целое большее ![]() . Заметим, что примерно такими параметрами
. Заметим, что примерно такими параметрами ![]() ,
, ![]() обладает сеть, построенная по технологии SCI, в которой для обмена данными используется коммуникационная библиотека MPI [2]. Указанная зависимость
обладает сеть, построенная по технологии SCI, в которой для обмена данными используется коммуникационная библиотека MPI [2]. Указанная зависимость ![]() соответствует коммуникационной сети с топологией типа квадратная «решетка».
соответствует коммуникационной сети с топологией типа квадратная «решетка».
3. Статическая балансировка
Для F-задачи статическую балансировку загрузки естественно организовать с использованием геометрической схемы распараллеливания [2], при которой узлы сетки ![]() разбиваются на
разбиваются на ![]() множеств
множеств ![]() по zузлов в каждой. Количество узлов множества
по zузлов в каждой. Количество узлов множества ![]() , принадлежащих множеству
, принадлежащих множеству ![]() , обозначим
, обозначим ![]() , а сумму этих величин обозначим
, а сумму этих величин обозначим ![]() . В сделанных предположениях схема параллельных вычислений при решении F-задачи с использованием статической балансировки загрузки имеет следующий вид.
. В сделанных предположениях схема параллельных вычислений при решении F-задачи с использованием статической балансировки загрузки имеет следующий вид.
Шаг 1. Host-процессор строит сетку ![]() и разбивает ее узлы на множества
и разбивает ее узлы на множества ![]() .
.
Шаг 2. Процессор ![]() выполняет следующие действия:
выполняет следующие действия:
· принимает от host-процессора координаты узлов множества ![]() ;
;
· последовательно для всех узлов этого множества определяет их принадлежность множеству ![]() ;
;
· вычисляет в каждом из ![]() узлов значение вектор-функции
узлов значение вектор-функции ![]() ;
;
· передает host-процессору вычисленные значения и заканчивает вычисления.
Шаг 3. Host-процессор на основе полученных значений вектор-функции ![]() вычисляет приближенное значение функционала
вычисляет приближенное значение функционала ![]() .
.
В соответствии с изложенной схемой время решения F-задачи на процессоре ![]() можно оценить величиной
можно оценить величиной
![]() ,
,
где ![]() ,
, ![]()
![]() - вычислительная загрузка процессора
- вычислительная загрузка процессора ![]() ,
, ![]() - его коммуникационная загрузка. При этом время параллельного решения всей F-задачи оценивается величиной
- его коммуникационная загрузка. При этом время параллельного решения всей F-задачи оценивается величиной
![]() .
.
Аналогично, оценка времени решения задачи на одном процессоре равна
![]() .
.
Если множество ![]() совпадает со всем параллелепипедом П, то, очевидно,
совпадает со всем параллелепипедом П, то, очевидно, ![]() ,
, ![]() и
и
![]() , (1)
, (1)
где ![]() ,
,
![]() . (2)
. (2)
Из (1), (2) следует, что для времени параллельного решения F-задачи имеет место оценка сверху
![]() ,
,
а для времени последовательного решения – оценка
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() .
.
Аналогично, из (1), (2) вытекает, что время параллельного решения F-задачи может быть оценено снизу величиной
![]() ,
,
а время решения задачи на одном процессоре – величиной
![]() .
.
Утверждение 1. Оценка ускорения сверху при статической балансировке равна
 ;
;
оценка ускорения снизу - равна
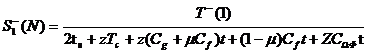 ●
●
Легко показать, что, как и следовало ожидать, при ![]() оценка
оценка ![]() стремится к максимально возможной, равной количеству процессоров в системе N, а оценка
стремится к максимально возможной, равной количеству процессоров в системе N, а оценка ![]() - стремится к единице.
- стремится к единице.
Утверждение 1 иллюстрирует Рис. 1. Рисунок показывает, что если положить ![]() , то уже при
, то уже при ![]() оценка ускорения сверху близка N, а оценка ускорения снизу слабо зависит от вычислительной сложности
оценка ускорения сверху близка N, а оценка ускорения снизу слабо зависит от вычислительной сложности ![]() и близка к единице.
и близка к единице.

Рис. 1. Оценки ускорения сверху и снизу при статической балансировке: ![]() .
.
4. Динамическая централизованная балансировка методом равномерной декомпозиции узлов
Разобьем узлы сетки ![]() на
на ![]() множеств
множеств ![]() ,
, ![]() и для простоты записи примем, что величина Z кратна
и для простоты записи примем, что величина Z кратна ![]() , так что каждое из множеств
, так что каждое из множеств ![]() содержит по
содержит по ![]() узлов (см. Рис. 2). Тогда схема параллельных вычислений при решении F-задачи с использованием динамической равномерной балансировки загрузки имеет следующий вид.
узлов (см. Рис. 2). Тогда схема параллельных вычислений при решении F-задачи с использованием динамической равномерной балансировки загрузки имеет следующий вид.
Шаг 1. Host-процессор строит сетку ![]() и разбивает ее узлы на множества
и разбивает ее узлы на множества ![]() .
.
Шаг 2. Процессор ![]() принимает от host-процессора координаты первого из нераспределенных множеств узлов
принимает от host-процессора координаты первого из нераспределенных множеств узлов ![]() ;
;
Шаг 3. Процессор ![]() для точек назначенного ему текущего множества узлов
для точек назначенного ему текущего множества узлов ![]() выполняет следующие действия:
выполняет следующие действия:
· определяет принадлежность каждого из этих узлов множеству ![]() ;
;
· если узел принадлежит множеству ![]() , то вычисляет в этом узле значение вектор-функции
, то вычисляет в этом узле значение вектор-функции ![]() ;
;
· после завершения обработки текущего множества узлов ![]() посылает host-процессору вычисленные значения
посылает host-процессору вычисленные значения ![]() .
.
Шаг 4. Если исчерпаны не все множества ![]() , то host-процессор посылает, а процессор
, то host-процессор посылает, а процессор ![]() принимает координаты следующего множества узлов
принимает координаты следующего множества узлов ![]() , которое обрабатывается процессором
, которое обрабатывается процессором ![]() аналогично шагу 3 и т.д.
аналогично шагу 3 и т.д.
Шаг 5. Если исчерпаны все множества ![]() , то host-процессор
, то host-процессор
· посылает освободившемуся процессору ![]() сообщение об окончании решения задачи,
сообщение об окончании решения задачи,
· после получения всех вычисленных значений вектор-функции ![]() от всех процессоров вычисляет приближенное значение функционала
от всех процессоров вычисляет приближенное значение функционала ![]() .
.

Рис. 2. Схема равномерного разбиения узлов для случая ![]() (параллелепипед П представляет собой отрезок
(параллелепипед П представляет собой отрезок ![]() ):
): ![]()
![]() , точками обозначены узлы сетки
, точками обозначены узлы сетки ![]() .
.
Заметим, что при ![]() , когда количество множеств
, когда количество множеств ![]() равно количеству процессоров в системе, динамическая равномерная балансировка вырождается в статическую балансировку. При
равно количеству процессоров в системе, динамическая равномерная балансировка вырождается в статическую балансировку. При ![]() каждое из множеств
каждое из множеств ![]() содержит по одному узлу сетки
содержит по одному узлу сетки ![]() .
.
Аналогично п. 3 вычислительные и коммуникационные затраты процессора ![]() на обработку множества узлов
на обработку множества узлов ![]() оцениваются величиной
оцениваются величиной
![]() ,
,
где ![]() ,
, ![]() - количество узлов множества
- количество узлов множества![]() , принадлежащих множеству
, принадлежащих множеству ![]() . Для времени параллельного решения F-задачи при этом имеем оценку
. Для времени параллельного решения F-задачи при этом имеем оценку
![]() ,
,
где ![]() - список номеров множеств
- список номеров множеств ![]() , назначенных процессору
, назначенных процессору ![]() ,
, ![]() - как и ранее, общее количество узлов сетки
- как и ранее, общее количество узлов сетки ![]() , принадлежащих множеству
, принадлежащих множеству ![]() .
.
Отсюда следует, что если множество ![]() совпадает со всем параллелепипедом П, то
совпадает со всем параллелепипедом П, то
![]() , (3)
, (3)
где ![]() .
.
В случае, когда вычислительные сложности всех узлов одинаковы, величина ![]() представляет собой количество множеств
представляет собой количество множеств ![]() , назначенных каждому из процессоров
, назначенных каждому из процессоров ![]() . Поэтому в качестве оценки сверху времени параллельного решения F-задачи из (3) имеем
. Поэтому в качестве оценки сверху времени параллельного решения F-задачи из (3) имеем
![]() .
.
Здесь учтено, что ![]() - количество узлов сетки
- количество узлов сетки ![]() , назначенных каждому из процессоров
, назначенных каждому из процессоров ![]() .
.
Объединим множества узлов ![]() в
в ![]() совокупностей
совокупностей ![]() по Nмножеств
по Nмножеств ![]() в каждой (см. Рис. 2). Если узел
в каждой (см. Рис. 2). Если узел ![]() принадлежит совокупности
принадлежит совокупности ![]() , то из (3) следует, что оценка снизу времени параллельного решения F-задачи равна
, то из (3) следует, что оценка снизу времени параллельного решения F-задачи равна
![]() . (4)
. (4)
Отметим, что здесь ![]() - общее количество узлов сетки
- общее количество узлов сетки ![]() , обработанных процессором
, обработанных процессором ![]() , которому выпал узел
, которому выпал узел ![]() . В формуле (4) учтено, что процессор, которому выпал узел
. В формуле (4) учтено, что процессор, которому выпал узел ![]() , в любом случае закончит работу не ранее других процессоров.
, в любом случае закончит работу не ранее других процессоров.
Так как вероятность того, что узел ![]() принадлежит совокупности узлов
принадлежит совокупности узлов ![]() , равна
, равна ![]() , из (4) следует, что средняя по
, из (4) следует, что средняя по ![]() оценка снизу времени параллельного решения F-задачи определяется выражением
оценка снизу времени параллельного решения F-задачи определяется выражением
![]()
![]() ,
,
где ![]() ,
, ![]() - символ математического ожидания.
- символ математического ожидания.
Аналогично, пользуясь известным свойством полигамма функции ![]() [8], легко получить выражение для средней по
[8], легко получить выражение для средней по ![]() оценки ускорения снизу при параллельном решении F-задачи
оценки ускорения снизу при параллельном решении F-задачи
![]()
![]() ,
,
где ![]() ,
, ![]() .
.
Утверждение 2. Оценка ускорения сверху при динамической равномерной балансировке равна
 ;
;
оценка ускорения снизу - равна
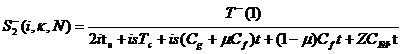 ;
;
средняя по ![]() оценка ускорения снизу – равна
оценка ускорения снизу – равна
![]() ,
,
где ![]() - символ полигамма функции и
- символ полигамма функции и ![]() ,
, ![]() ●
●
Анализ оценка ускорения сверху. Оценка ![]() принимает минимальное значение при
принимает минимальное значение при ![]() и максимальное значение – при
и максимальное значение – при ![]() . Так что
. Так что ![]() , а
, а ![]() . Легко видеть, при
. Легко видеть, при ![]() оценка сверху ускорения при динамической равномерной балансировке
оценка сверху ускорения при динамической равномерной балансировке ![]() меньше такой же оценки
меньше такой же оценки ![]() при статической балансировке. Потеря ускорения обусловлена тем фактом, что при динамической равномерной балансировке количество актов обмена каждого из процессоров
при статической балансировке. Потеря ускорения обусловлена тем фактом, что при динамической равномерной балансировке количество актов обмена каждого из процессоров ![]() с host-процессором больше, чем при статической балансировке, и поэтому выше коммуникационные расходы, обусловленные латентностью коммуникационной сети.
с host-процессором больше, чем при статической балансировке, и поэтому выше коммуникационные расходы, обусловленные латентностью коммуникационной сети.
Таким образом, относительная оценка ускорения сверху при динамической равномерной балансировке удовлетворяет неравенству ![]() , где нижняя граница
, где нижняя граница ![]() соответствует нижней границе
соответствует нижней границе ![]() . Легко показать, что при
. Легко показать, что при ![]() величина
величина ![]() стремится к нулю (см. Рис. 3).
стремится к нулю (см. Рис. 3).
Зависимость ![]() иллюстрирует Рис. 3. Рисунок показывает, что уже при
иллюстрирует Рис. 3. Рисунок показывает, что уже при ![]() потери ускорения не превышают 10%. Отметим также слабую зависимость величины
потери ускорения не превышают 10%. Отметим также слабую зависимость величины ![]() от количества процессоров в системе N.
от количества процессоров в системе N.

Рис. 3. Нижняя граница относительной оценки ускорения сверху при динамической равномерной балансировке: ![]() .
.
Анализ оценки ускорения снизу. Легко показать, что оценка ![]() в треугольнике допустимых значений
в треугольнике допустимых значений ![]() принимает свое минимальное значение при
принимает свое минимальное значение при ![]() , а свое максимальное значение - при
, а свое максимальное значение - при ![]() ,
, ![]() . Поэтому относительная оценка ускорения снизу при динамической равномерной балансировке удовлетворяет неравенству
. Поэтому относительная оценка ускорения снизу при динамической равномерной балансировке удовлетворяет неравенству ![]() , где нижняя граница этой оценки
, где нижняя граница этой оценки ![]() соответствует величине
соответствует величине ![]() , а ее верхняя граница
, а ее верхняя граница ![]() - величине
- величине ![]() . Отметим, что ситуация
. Отметим, что ситуация ![]() означает, что каждое из множеств
означает, что каждое из множеств ![]() содержит по одному узлу сетки
содержит по одному узлу сетки ![]() . Так что граница
. Так что граница ![]() достигается в ситуации, когда узел
достигается в ситуации, когда узел ![]() - это последний узел, распределенный некоторому процессору
- это последний узел, распределенный некоторому процессору ![]() . Аналогично, граница
. Аналогично, граница ![]() достигается, когда узел
достигается, когда узел ![]() - это первый узел, распределенный процессору
- это первый узел, распределенный процессору ![]() .
.
Граница ![]() является отрицательной величиной и имеет, таким образом, смысл потери ускорения по сравнению со статической балансировкой. Аналогично, граница
является отрицательной величиной и имеет, таким образом, смысл потери ускорения по сравнению со статической балансировкой. Аналогично, граница ![]() имеет смысл приобретения ускорения. Легко показать, что при
имеет смысл приобретения ускорения. Легко показать, что при ![]() величина
величина ![]() стремится к нулю, а величина
стремится к нулю, а величина ![]() стремится к
стремится к ![]() .
.
Зависимости ![]() ,
, ![]() иллюстрирует Рис. 4. Рисунок показывает, что при небольшом количестве процессоров (~10) и вычислительной сложности
иллюстрирует Рис. 4. Рисунок показывает, что при небольшом количестве процессоров (~10) и вычислительной сложности ![]() относительное увеличение ускорения может превышать 10 раз, а его относительное уменьшение – не более двух раз.
относительное увеличение ускорения может превышать 10 раз, а его относительное уменьшение – не более двух раз.

Рис. 4. Нижняя и верхняя границы относительной оценки ускорения снизу при динамической равномерной балансировке: ![]() ,
, ![]() .
.
5. Динамическая централизованная балансировка загрузки методом экспоненциальной декомпозиции узлов
На k-ой итерации экспоненциальной декомпозиции узлов среди оставшихся ![]() узлов сетки
узлов сетки ![]() выделяется множество узлов
выделяется множество узлов ![]() , содержащее
, содержащее ![]() узлов, где целая положительная величина
узлов, где целая положительная величина ![]()
![]() - коэффициент декомпозиции. Для простоты записи положим, что величины
- коэффициент декомпозиции. Для простоты записи положим, что величины ![]() кратны
кратны ![]() , а величины
, а величины ![]() кратна количеству процессоров в системе N, так что подмножества
кратна количеству процессоров в системе N, так что подмножества ![]() ,
, ![]() содержат по
содержат по ![]() узлов (см. Рис. 5). Тогда схема параллельных вычислений при решении F-задачи с использованием динамической экспоненциальной балансировки загрузки имеет следующий вид.
узлов (см. Рис. 5). Тогда схема параллельных вычислений при решении F-задачи с использованием динамической экспоненциальной балансировки загрузки имеет следующий вид.
Шаг 1. Host-процессор строит сетку ![]() и присваивает счетчику количества итераций k значение 1 (принято, что
и присваивает счетчику количества итераций k значение 1 (принято, что ![]() ).
).
Шаг 2. Если исчерпаны не все узлы сетки ![]() , то host-процессор выделяет среди
, то host-процессор выделяет среди ![]() узлов этой сетки множество узлов
узлов этой сетки множество узлов ![]() .
.
Шаг 3. Если множество узлов ![]() не исчерпано, то host-процессор передает, а процессор
не исчерпано, то host-процессор передает, а процессор ![]() принимает от него координаты узлов подмножества
принимает от него координаты узлов подмножества ![]() .
.
Шаг 4. Процессор ![]() для узлов текущего подмножества
для узлов текущего подмножества ![]() выполняет следующие действия:
выполняет следующие действия:
· определяет принадлежность каждого из этих узлов множеству ![]() ;
;
· если узел принадлежит множеству ![]() , то вычисляет в этом узле значение вектор-функции
, то вычисляет в этом узле значение вектор-функции ![]() ;
;
· после завершения обработки текущего подмножества узлов ![]() посылает host-процессору найденные им значения вектор-функции
посылает host-процессору найденные им значения вектор-функции ![]() ;
;
Шаг 5. Если множество узлов ![]() исчерпано, то host-процессор выполняет присваивания k=k+1,
исчерпано, то host-процессор выполняет присваивания k=k+1, ![]() и переходит к шагу 2.
и переходит к шагу 2.
Шаг 6. Если исчерпаны все узлы сетки ![]() , то host-процессор
, то host-процессор
· посылает освободившемуся процессору ![]() сообщение об окончании решения задачи,
сообщение об окончании решения задачи,
· после получения всех вычисленных значений вектор-функций ![]() от всех процессоров вычисляет приближенное значение функционала
от всех процессоров вычисляет приближенное значение функционала ![]() .
.

Рис. 5. Схема экспоненциального разбиения узлов для случая ![]() :
: ![]()
![]() , точками обозначены узлы сетки
, точками обозначены узлы сетки ![]() .
.
Заметим, что количества узлов ![]() в соседних подмножествах, назначенных процессору
в соседних подмножествах, назначенных процессору ![]() , не обязательно различны – возможна ситуация, когда процессор
, не обязательно различны – возможна ситуация, когда процессор ![]() получит два и более подмножества узлов из одного множества
получит два и более подмножества узлов из одного множества ![]() .
.
Ограничимся далее случаем ![]() . При этом общее количество множеств
. При этом общее количество множеств ![]() равно
равно ![]() , где
, где 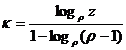 =
=![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() (см. Рис. 5). Подчеркнем, что в данном случае, в отличие от п. 4, величина
(см. Рис. 5). Подчеркнем, что в данном случае, в отличие от п. 4, величина ![]() не является независимой величиной (а определяется величинами Z, N).
не является независимой величиной (а определяется величинами Z, N).
Сумма вычислительных и коммуникационных затрат ![]() процессора
процессора ![]() на обработку подмножества узлов
на обработку подмножества узлов ![]() оценим величиной
оценим величиной
![]()
![]() +
+![]() +
+![]() +
+![]() ,
,
где ![]() ,
, ![]() ;
; ![]() - количество узлов подмножества
- количество узлов подмножества ![]() , принадлежащих множеству
, принадлежащих множеству ![]() . Отсюда имеем оценку времени параллельного решения F-задачи
. Отсюда имеем оценку времени параллельного решения F-задачи
![]()
![]() +
+![]() ,
,
где ![]() - список номеров подмножеств
- список номеров подмножеств ![]() , назначенных процессору
, назначенных процессору ![]() .
.
Если множество ![]() совпадает со всем параллелепипедом П, то
совпадает со всем параллелепипедом П, то ![]() ,
, ![]() ,
,
![]() ,
,
![]() . (5)
. (5)
Из (5) следует, что оценка сверху времени параллельного решения F-задачи равна
![]() .
.
Если узел ![]() принадлежит множеству
принадлежит множеству ![]() ,
, ![]() , то время параллельного решения F-задачи оценивается снизу величиной
, то время параллельного решения F-задачи оценивается снизу величиной
![]() . (6)
. (6)
Здесь величина ![]() - общее количество узлов, назначенных для обработки процессору, которому выпал узел
- общее количество узлов, назначенных для обработки процессору, которому выпал узел ![]() . Если
. Если ![]() , то
, то ![]() - сумма
- сумма ![]() членов геометрической прогрессии
членов геометрической прогрессии ![]() ; если
; если ![]() , то
, то ![]() . Формула (6) учитывает тот факт, что процессор, которому выпал узел
. Формула (6) учитывает тот факт, что процессор, которому выпал узел ![]() , закончит работу не ранее других процессоров.
, закончит работу не ранее других процессоров.
Поскольку вероятность того, что узел ![]() принадлежит множеству узлов
принадлежит множеству узлов ![]() , равна
, равна ![]() при
при ![]() и равна
и равна ![]() при
при ![]() , то средняя по
, то средняя по ![]() оценка снизу времени параллельного решения F-задачи равна
оценка снизу времени параллельного решения F-задачи равна
![]()
![]() ,
,
где
![]() ;
;
![]() =
=![]() =
=![]() .
.
Заметим, что в оценке ![]() приближенность равенства обусловлена только тем фактом, что для простоты записи мы не использовали в ней, как следовало бы, целочисленные аппроксимации величин
приближенность равенства обусловлена только тем фактом, что для простоты записи мы не использовали в ней, как следовало бы, целочисленные аппроксимации величин ![]() .
.
Аналогично, средняя по ![]() оценка ускорения снизу при параллельном решении F-задачи может быть вычислена по формуле
оценка ускорения снизу при параллельном решении F-задачи может быть вычислена по формуле
 .
.
Утверждение 3. Оценка ускорения сверху при динамической экспоненциальной балансировке равна
![]() ;
;
оценка ускорения снизу - равна
 ,
,
где![]() , если
, если ![]() , и
, и ![]() ●
●
Анализ оценки ускорения сверху. Относительная оценка ускорения сверху ![]() удовлетворяет неравенству
удовлетворяет неравенству ![]() . Т.е. при динамической экспоненциальной балансировке по сравнению со статической балансировкой могут иметь место потери ускорения. Так же, как при динамической равномерной балансировке, эти потери обусловлены латентностью коммуникационной сети. Легко показать, что при
. Т.е. при динамической экспоненциальной балансировке по сравнению со статической балансировкой могут иметь место потери ускорения. Так же, как при динамической равномерной балансировке, эти потери обусловлены латентностью коммуникационной сети. Легко показать, что при ![]() величина
величина ![]() стремится к нулю.
стремится к нулю.
Зависимость ![]() иллюстрирует Рис. 6, который показывает, что с ростом вычислительной сложности
иллюстрирует Рис. 6, который показывает, что с ростом вычислительной сложности ![]() потери ускорения быстро уменьшаются и уже при вычислительной сложности
потери ускорения быстро уменьшаются и уже при вычислительной сложности ![]() не превышают 3%. Отметим, что с ростом количества процессоров в системе потери ускорения по абсолютной величине возрастают.
не превышают 3%. Отметим, что с ростом количества процессоров в системе потери ускорения по абсолютной величине возрастают.

Рис. 6. Относительная оценка ускорения сверху при динамической экспоненциальной балансировке: ![]() .
.
Анализ оценки ускорения снизу Оценка ![]() достигает своего минимального значения при
достигает своего минимального значения при ![]() , а своего максимального значения – при
, а своего максимального значения – при ![]() . Отсюда следует, что относительная оценка ускорения снизу при динамической экспоненциальной балансировке удовлетворяет неравенству
. Отсюда следует, что относительная оценка ускорения снизу при динамической экспоненциальной балансировке удовлетворяет неравенству ![]() . Здесь нижняя граница
. Здесь нижняя граница ![]() соответствует величине
соответствует величине ![]() , т.е., как и ожидалось, достигается в случае, когда узел
, т.е., как и ожидалось, достигается в случае, когда узел ![]() принадлежит последнему из множеств
принадлежит последнему из множеств ![]() . Аналогично, верхняя граница
. Аналогично, верхняя граница ![]() соответствует величине
соответствует величине ![]() , т.е. достигается, когда узел
, т.е. достигается, когда узел ![]() принадлежит первому из множеств
принадлежит первому из множеств ![]() .
.
Легко показать, что при ![]() оценка
оценка ![]() стремится к величине
стремится к величине ![]() . Поскольку
. Поскольку ![]() при всех допустимых k, то отсюда следует, что оценка
при всех допустимых k, то отсюда следует, что оценка ![]() неотрицательна. Т.е. оценка ускорения снизу при динамической экспоненциальной балансировке не хуже такой же оценки при статической балансировке. Далее, отсюда же следует, что при
неотрицательна. Т.е. оценка ускорения снизу при динамической экспоненциальной балансировке не хуже такой же оценки при статической балансировке. Далее, отсюда же следует, что при ![]() нижняя граница
нижняя граница ![]() стремится к нулю, а верхняя граница
стремится к нулю, а верхняя граница ![]() стремится к величине
стремится к величине ![]() .
.
Зависимости ![]() ,
, ![]() иллюстрирует Рис. 7. Рисунок показывает, что при небольшом количестве процессоров (до ~10) и вычислительной сложности
иллюстрирует Рис. 7. Рисунок показывает, что при небольшом количестве процессоров (до ~10) и вычислительной сложности ![]() относительное увеличение оценки ускорения снизу может превышать 30 раз. Отметим, что в тех же условиях динамическая равномерная балансировка обеспечивает относительное увеличение ускорения до примерно 15 раз (см. п. 4).
относительное увеличение оценки ускорения снизу может превышать 30 раз. Отметим, что в тех же условиях динамическая равномерная балансировка обеспечивает относительное увеличение ускорения до примерно 15 раз (см. п. 4).
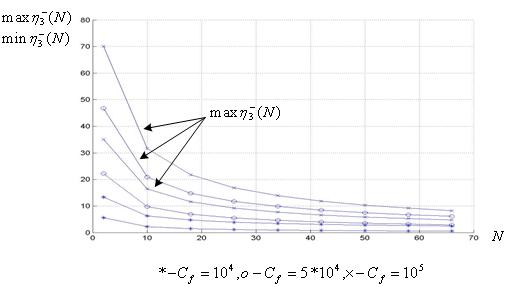
Рис. 7. Нижняя и верхняя границы относительной оценки ускорения снизу при динамической экспоненциальной балансировке: ![]() ,
, ![]() .
.
6. Динамическая децентрализованная балансировка загрузки диффузным методом
Схема параллельных вычислений при решении F-задачи с использованием метода диффузной балансировки загрузки имеет следующий вид.
Шаг 1. Host-процессор строит сетку ![]() и разбивает ее узлы на N множеств
и разбивает ее узлы на N множеств ![]() по zузлов в каждом.
по zузлов в каждом.
Шаг 2. Процессор ![]() :
:
· принимает от host-процессора координаты узлов множества ![]() ;
;
· последовательно для всех узлов этого множества определяет их принадлежность множеству ![]() ;
;
· если узел принадлежит множеству ![]() , то вычисляет в этом узле значение вектор-функции
, то вычисляет в этом узле значение вектор-функции ![]() ;
;
· передает host-процессору вычисленные значения вектор-функции ![]() .
.
Шаг 3. Если процессор ![]() закончил вычисления и передал host-процессору вычисленные значения вектор функции
закончил вычисления и передал host-процессору вычисленные значения вектор функции ![]() , то этот процессор:
, то этот процессор:
· посылает запрос некоторому процессору ![]() ;
;
· если процессор ![]() имеет необработанные узлы, то процессор
имеет необработанные узлы, то процессор ![]() принимает от процессора
принимает от процессора ![]() координаты
координаты ![]() части из них;
части из них;
· посылает сообщение host-процессору об этом факте (для того, чтобы host-процессор имел возможность определить момент завершения решения задачи).
Шаг 4. Процессор ![]()
· в каждом из принятых узлов вычисляет значение вектор-функции ![]() ,
,
· передает host-процессору вычисленные значения вектор-функции ![]() .
.
Шаг 5. Host-процессор после получения от всех процессоров сообщений о завершении вычислений посылает всем им сообщение о завершении решения задачи и на основе полученных значение вектор-функции ![]() вычисляет приближенное значение функционала
вычисляет приближенное значение функционала ![]() .
.
Здесь ![]() - коэффициент декомпозиции остатка узлов. Ограничимся случаем, когда
- коэффициент декомпозиции остатка узлов. Ограничимся случаем, когда ![]() и множество
и множество ![]() совпадает со всем параллелепипедом П.
совпадает со всем параллелепипедом П.
Легко видеть, что если вычислительные сложности ![]() одинаковы и равны
одинаковы и равны ![]() , то при диффузной балансировке перераспределения узлов не производится и диффузная балансировка превращается в статическую балансировку. Поэтому оценка ускорения сверху совпадает с такой же оценкой при статической балансировке (см. п. 1).
, то при диффузной балансировке перераспределения узлов не производится и диффузная балансировка превращается в статическую балансировку. Поэтому оценка ускорения сверху совпадает с такой же оценкой при статической балансировке (см. п. 1).
Положим, что узлом ![]() является узел
является узел ![]() ,
, ![]() . Тогда время параллельного решения F-задачи может быть оценено снизу величиной
. Тогда время параллельного решения F-задачи может быть оценено снизу величиной
![]() , (7)
, (7)
где ![]()
![]()
![]() - расходы процессора, которому выпал для обработки узел
- расходы процессора, которому выпал для обработки узел ![]() , обусловленные перераспределением между другими процессорами системы необработанных узлов
, обусловленные перераспределением между другими процессорами системы необработанных узлов ![]() ,
, ![]() (такие узлы имеются, очевидно, в случае, когда
(такие узлы имеются, очевидно, в случае, когда ![]() ). Заметим, что формула (7) учитывает, что процессор, которому выпал узел
). Заметим, что формула (7) учитывает, что процессор, которому выпал узел ![]() , закончит работу не ранее других процессоров.
, закончит работу не ранее других процессоров.
Пренебрежем вычислительными расходами на декомпозицию необработанных узлов. Тогда величина ![]() включает в себя только коммуникационные расходы и ее оценка при
включает в себя только коммуникационные расходы и ее оценка при ![]() равна
равна ![]() , а при
, а при ![]() - равна
- равна ![]() . Здесь
. Здесь ![]() и точное равенство имеет место, если величина
и точное равенство имеет место, если величина ![]() есть целая степень двух.
есть целая степень двух.
Легко видеть, что вероятность того, что узел ![]() является
является ![]() -м узлом одного из множеств узлов
-м узлом одного из множеств узлов ![]() , равна
, равна ![]() . Поэтому из (7) следует, что средняя по
. Поэтому из (7) следует, что средняя по ![]() оценка снизу времени параллельного решения F-задачи равна
оценка снизу времени параллельного решения F-задачи равна
![]()
![]()
![]() ,
,
где ![]() ,
, ![]() и приближенность равенства обусловлена только тем фактом, что для простоты записи здесь не использованы целочисленные аппроксимации величин
и приближенность равенства обусловлена только тем фактом, что для простоты записи здесь не использованы целочисленные аппроксимации величин ![]() .
.
Аналогично, средняя по ![]() оценка ускорения снизу при параллельном решении F-задачи может быть вычислена по формуле
оценка ускорения снизу при параллельном решении F-задачи может быть вычислена по формуле
 .
.
Утверждение 4. Оценка ускорения сверху при диффузной балансировке равна оценке ускорения сверху при статической балансировке, т.е.
![]() ;
;
оценка ускорения снизу - равна
![]()
 ,
,
где ![]() ●
●
Анализ оценки ускорения снизу. Легко показать, что поведение оценки ![]() , как функции величины
, как функции величины ![]() , зависит от вычислительной сложности
, зависит от вычислительной сложности ![]() . При выполнении неравенства
. При выполнении неравенства
 (8)
(8)
оценка ![]() является возрастающей функцией величины
является возрастающей функцией величины ![]() ; при выполнении неравенства
; при выполнении неравенства
![]() - (9)
- (9)
убывающей функцией этой же величины. Например, если пренебречь величиной ![]() , то при тестовых значениях параметров задачи и МВС имеем:
, то при тестовых значениях параметров задачи и МВС имеем: ![]() ,
, ![]() .
.
При промежуточных значениях вычислительной сложности ![]() на интервале
на интервале ![]() оценка
оценка ![]() является возрастающей функцией величины
является возрастающей функцией величины ![]() , а на интервале
, а на интервале ![]() - убывающей функцией этой же величины. Здесь
- убывающей функцией этой же величины. Здесь
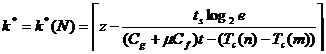 ,
,
![]() - ближайшее целое большее
- ближайшее целое большее ![]() .
.
Относительная оценка ускорения снизу при диффузной балансировке ![]() удовлетворяет неравенству
удовлетворяет неравенству ![]() . При выполнении условия (8) нижняя граница
. При выполнении условия (8) нижняя граница ![]() соответствует величине
соответствует величине ![]() , а верхняя граница
, а верхняя граница ![]() – величине
– величине ![]() . Аналогично, при выполнении условия (9) нижняя граница соответствует величине
. Аналогично, при выполнении условия (9) нижняя граница соответствует величине ![]() , а верхняя граница – величине
, а верхняя граница – величине ![]() .
.
Ситуация ![]() означает, что узел
означает, что узел ![]() является последним из узлов некоторого множества
является последним из узлов некоторого множества ![]() . Поэтому процессор, которому выпал узел
. Поэтому процессор, которому выпал узел ![]() , должен будет обработать все узлы множества
, должен будет обработать все узлы множества ![]() , т.е. перераспределение узлов в данном случае не будет иметь место. Таким образом, при
, т.е. перераспределение узлов в данном случае не будет иметь место. Таким образом, при ![]() диффузная балансировка вырождается в статическую балансировку и при выполнении условия (8)
диффузная балансировка вырождается в статическую балансировку и при выполнении условия (8) ![]() , а при выполнении условия (9) -
, а при выполнении условия (9) - ![]() .
.
Поскольку при выполнении условия (8) верхняя граница относительной оценки ускорения снизу ![]() равна нулю, величина
равна нулю, величина ![]() отрицательна. Таким образом, при выполнении условия (8) имеют место потери ускорения по сравнению со статической балансировкой. Потери ускорения обусловлены расходами на перераспределение между другими процессорами системы необработанных узлов, т.е. компонентой
отрицательна. Таким образом, при выполнении условия (8) имеют место потери ускорения по сравнению со статической балансировкой. Потери ускорения обусловлены расходами на перераспределение между другими процессорами системы необработанных узлов, т.е. компонентой ![]() в выражении (7).
в выражении (7).
Напротив, при выполнении условия (9) нижняя граница относительной оценки ускорения снизу ![]() равна нулю. Поэтому величина
равна нулю. Поэтому величина ![]() положительна, т.е. при выполнении условия (9) имеет место приобретение ускорения по сравнению со статической балансировкой.
положительна, т.е. при выполнении условия (9) имеет место приобретение ускорения по сравнению со статической балансировкой.
Зависимость ![]() при малой вычислительной сложности
при малой вычислительной сложности ![]() иллюстрирует Рис.8, зависимость
иллюстрирует Рис.8, зависимость ![]() при большой вычислительной сложности
при большой вычислительной сложности ![]() иллюстрирует Рис.9.
иллюстрирует Рис.9.

Рис. 8. Нижняя граница относительной оценки ускорения снизу при диффузной балансировке: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()

Рис. 9. Верхняя граница относительной оценки ускорения снизу при диффузной балансировке: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
Рисунки 8, 9 показывают, что при небольшом количестве процессоров (до ~10) и малой вычислительной сложности ![]() потери ускорения могут достигать 50%, а приобретения ускорения при большой вычислительной сложности
потери ускорения могут достигать 50%, а приобретения ускорения при большой вычислительной сложности ![]() – могут превышать 4 раз.
– могут превышать 4 раз.
Легко показать, что при ![]() величина
величина ![]() стремится к величине
стремится к величине ![]() . Отсюда следует, что в пределе аналогично динамической равномерной балансировке верхняя граница
. Отсюда следует, что в пределе аналогично динамической равномерной балансировке верхняя граница ![]() стремится к величине
стремится к величине ![]() .
.
7. Заключение
Результаты работы позволяют выполнить сравнительный анализ эффективности статической, динамической равномерной, динамической экспоненциальной и диффузной балансировки загрузки при решении F-задачи в зависимости от ее параметров и параметров используемой МВС. Это, в конечном счете, позволяет сделать обоснованный выбор метода балансировки загрузки или совокупности таких методов для решения конкретной F-задачи.
Выполненное исследование не закрывает всех вопросов, связанных с эффективностью указанных методов балансировки. Например, не удается аналитическое определение оптимального количестве множеств ![]() для динамической равномерной балансировки при промежуточных значениях дисперсии вычислительной сложности
для динамической равномерной балансировки при промежуточных значениях дисперсии вычислительной сложности ![]() . Поэтому предполагаются дополнительные исследования с помощью имитационного моделирования [9] и натурных вычислительных экспериментов.
. Поэтому предполагаются дополнительные исследования с помощью имитационного моделирования [9] и натурных вычислительных экспериментов.
Литература.
1. Foster I. Designing and building parallel programs: concept and tools for parallel software engineering. – Boston.: Addison-Wesley, 1995.
2. Воеводин В.В., Воеводин Вл., В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2004.
3. Карпенко А.П., Шурайц Ю.М. Параллелизм методов интегрирования дифференциальных уравнений в частных производных // Автоматика и телемеханика. - 1992, №10, c. 3-20.
4. Танненбаум Э. Современные операционные системы. 2-е изд – СПб.:Питер.-1038 с.
5. Карпенко А.П., Пупков К.А. Моделирование динамических систем на транспьютерных сетях -М.: Биоинформ, 1995.
6. Волков К.Н. Применение средств параллельного программирования для решения задач механики жидкостей и газа на многопроцессорных вычислительных системах // Вычислительные методы и программирование. - 2006, Т.7, с. 69 – 84.
7. Gubenko G. Dynamic load Balancing for Distributed Memory Multiprocessors // Journal of parallel and distributed computing. – 1989. 7, pp. 279 -301.
8. Бейтман Г., Эрдейи Л. высшие трансцендентные функции. Гипергеометрические функции. Функции Лежандра. –М., Наука, 1965.
9. Шрайбер Т.Дж. Моделирование на GPSS. –М., Машиностроение, 1980.
Публикации с ключевыми словами: динамическая балансировка, статическая балансировка, решение вычислительных задач, многопроцессорые вычислительные системы, МВС
Публикации со словами: динамическая балансировка, статическая балансировка, решение вычислительных задач, многопроцессорые вычислительные системы, МВС
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



