научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 01, январь 2014
DOI: 10.7463/0114.0673360
| УДК 539.3 | Россия, Нижегородский государственный технический университет им. Р. Е. Алексеева |
Введение
В различных областях техники, в особенности в транспортном машиностроении, используются ударные амортизаторы – устройства, останавливающие движение тел. Торможение осуществляется путём поглощения кинетической энергии [1][2].
К некоторым конструктивным элементам, поглощающим энергию движения различных тел, применима расчётная схема оболочки. При этом эффективное поглощение энергии сопряжено с существенным изменением первоначальной формы.
Большие деформации упругих оболочек с существенным изменением формы рассмотрены в работах А.В. Погорелова [3]. Большие деформации с существенным изменением формы пластической сферической оболочки под действием локальной нагрузки рассмотрены в работе [4], конструктивно-ортотропной пластической цилиндрической оболочки в работе [5].
В данной работе строится аналитическая модель деформирования пластической конической оболочки. В процессе осесимметричного деформирования внутренняя поверхность оболочки становится наружной, а наружная поверхность - внутренней.
В книге [6] описан амортизатор, в котором аналогичной деформацией круглой трубы осуществляется поглощение энергии.
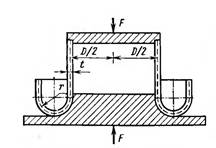
Рис.1 Схема трубчатого амортизатора из книги Дж. Фентона [6].
Недостатком такой конструкции является большая окружная деформация, которую сможет выдержать без разрушения не всякий материал. Устранить данный недостаток можно применением конической деформируемой оболочки, например по схеме, показанной на рис.2. Здесь вертикальное движение верхней недеформируемой оболочки вызывает деформирование нижней конической оболочки с преобразованием внутренней поверхности в наружную. При этом радиальные перемещения меньше, чем цилиндрической оболочки (круглой трубы), следовательно, меньше и кольцевые деформации.

Рис.2 Схема конического амортизатора
Целью данной работы является построение аналитической модели деформирования пластической конической оболочки и применение данной модели для исследования влияния геометрических параметров оболочки на процесс поглощения энергии.
Материал конической оболочки считается жёстко – идеально пластическим. Использована теория предельного равновесия [7], [8]. Связь перемещений и деформаций соответствует теории тонких оболочек, изложенной в монографии [9]. Не деформированная и деформированная срединная поверхность считается осесимметричной.
1 Вывод аналитических зависимостей для расчёта параметров деформирования конической оболочки
Рассмотрим коническую оболочку с углом наклона образующей ![]() толщины
толщины ![]() из жестко - идеальнопластического материала, претерпевшую деформацию под действием продольного осевого усилия
из жестко - идеальнопластического материала, претерпевшую деформацию под действием продольного осевого усилия ![]() , где
, где ![]() - нагрузка, распределённая по окружности радиуса
- нагрузка, распределённая по окружности радиуса ![]() по краю оболочки. Предположим, что деформированная часть оболочки состоит из торовой части с радиусом образующей окружности
по краю оболочки. Предположим, что деформированная часть оболочки состоит из торовой части с радиусом образующей окружности ![]() и конической части с углом наклона образующей
и конической части с углом наклона образующей ![]() (отложен против часовой стрелки на рис. 3).
(отложен против часовой стрелки на рис. 3).
Полагаем, что наружная деформированная коническая часть двигается поступательно как жёсткое тело, а деформируется только торовая часть. Найдем величину продольного усилия, необходимого для продолжения процесса деформирования, используя кинематический метод.
1.1Определение энергии деформации оболочки
На рис. 3 вертикальной штрих-пунктирной линией показана ось симметрии. Под углом ![]() по часовой стрелке показана образующая (меридиан) недеформированной конической оболочки. Толстой сплошной линией показана образующая конической оболочки в рассматриваемый момент времени, соответствующий перемещению верхнего края конической оболочки вдоль оси симметрии
по часовой стрелке показана образующая (меридиан) недеформированной конической оболочки. Толстой сплошной линией показана образующая конической оболочки в рассматриваемый момент времени, соответствующий перемещению верхнего края конической оболочки вдоль оси симметрии ![]() .
.

Рис.3 . Схема деформирования образующей конической оболочки
Рассмотрим деформацию конической оболочки при дальнейшем взаимном перемещении её краёв. Считаем, что относительное удлинение образующей равно нулю. Пусть малая часть недеформированной оболочки с образующей длиной ![]() сдеформировалась в торовую часть, а наружная часть торовой оболочки с образующей такой же длины сдеформировалась в наружную коническую оболочку. При этом длина образующей наружной оболочки увеличилась на величину
сдеформировалась в торовую часть, а наружная часть торовой оболочки с образующей такой же длины сдеформировалась в наружную коническую оболочку. При этом длина образующей наружной оболочки увеличилась на величину ![]() . Толстой штриховой линией с коротким штрихом показана образующая деформированной конической оболочки после искривления части образующей малой длины
. Толстой штриховой линией с коротким штрихом показана образующая деформированной конической оболочки после искривления части образующей малой длины ![]() . Вычислим деформации элемента оболочки при деформировании из первоначального положения в положение в наружной недеформируемой конической оболочке. Полагаем, что размеры криволинейной части образующей малы по сравнению с расстоянием от оси симметрии
. Вычислим деформации элемента оболочки при деформировании из первоначального положения в положение в наружной недеформируемой конической оболочке. Полагаем, что размеры криволинейной части образующей малы по сравнению с расстоянием от оси симметрии ![]() .
.
Происходит искривление и распрямление элемента конической оболочки с площадью срединной поверхности ![]() в направлении образующей срединной поверхности на величину кривизны
в направлении образующей срединной поверхности на величину кривизны  , распрямление и искривление в кольцевом направлении на величину кривизны
, распрямление и искривление в кольцевом направлении на величину кривизны ![]() .
.
Также происходит перемещение в направлении, перпендикулярном оси симметрии. Точка ![]() с радиальной координатой
с радиальной координатой ![]() на образующей недеформированной конической оболочки перемещается в положение
на образующей недеформированной конической оболочки перемещается в положение![]() на образующей деформированной конической поверхности. Увеличение расстояние от оси симметрии
на образующей деформированной конической поверхности. Увеличение расстояние от оси симметрии ![]() при условии отсутствия линейной деформации образующей равно:
при условии отсутствия линейной деформации образующей равно:
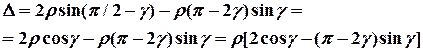
При этом кольцевая цепная деформация равна:
![]() .
.
Вычислим энергию деформации оболочки, приняв поверхность текучести, описанную относительно точной поверхности текучести:
![]() ;
; ![]() ,
,
где ![]() - предел текучести материала оболочки;
- предел текучести материала оболочки;
![]() – нормальные усилия в нормальных конических сечениях и осевых сечениях соответственно;
– нормальные усилия в нормальных конических сечениях и осевых сечениях соответственно;
![]() – изгибающие моменты в нормальных конических сечениях и осевых сечениях соответственно.
– изгибающие моменты в нормальных конических сечениях и осевых сечениях соответственно.
Энергия (диссипация), связанная с искривлением и распрямлением образующей конической оболочки (изменением кривизны образующей на величину ![]() ):
):
 .
.
Энергия (диссипация), связанная с изменением кривизны (на величину ![]() ) в кольцевом направлении:
) в кольцевом направлении:
![]()
Энергия (диссипация), связанная с цепными кольцевыми деформациями:
![]()
Суммарная диссипация в оболочке:
![]()
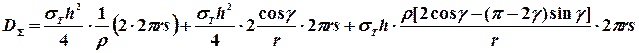
Считая величину ![]() параметром, определяющим процесс деформирования, найдём суммарную мощность диссипации:
параметром, определяющим процесс деформирования, найдём суммарную мощность диссипации:

1.2 Определение продольного усилия деформирования
Малое осевое перемещение края деформированной части оболочки при отгибе внутренней конической оболочки на малую величину ![]() равно
равно ![]() (см. рис. 3). Работа внешней нагрузки
(см. рис. 3). Работа внешней нагрузки ![]() при этом равна :
при этом равна :
![]()
Мощность внешней нагрузки:
![]()
Приравнивая мощность внешней нагрузки суммарной мощности диссипации, найдём величину продольного усилия:


В соответствии c кинематической теоремой теории предельного равновесия [7], [8] определим величину радиуса образующей окружности тора ![]() , при которой нагрузка
, при которой нагрузка ![]() минимальна:
минимальна:


Откуда находим:
 (2)
(2)
Обозначим
 (3)
(3)
Тогда
 (4)
(4)
Подставляя ![]() в формулу (1) для
в формулу (1) для ![]() , найдём усилие, необходимое для продолжения деформирования:
, найдём усилие, необходимое для продолжения деформирования:

 (5)
(5)
Из рисунка 3 определяем величину осевого перемещения точек приложения нагрузки:
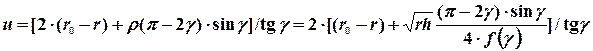 (6)
(6)
Таким образом, для каждой величины радиальной координаты ![]() можно вычислить величины перемещения (6) и нагрузки (5), то есть определить зависимость нагрузка – перемещение.
можно вычислить величины перемещения (6) и нагрузки (5), то есть определить зависимость нагрузка – перемещение.
1.3 Случай ![]()
Для цилиндрической оболочки радиуса ![]() , полагая в формулах(2),(3),(4),(5)
, полагая в формулах(2),(3),(4),(5) ![]() , получим:
, получим:
![]() (7)
(7)
 (8)
(8)
 (9)
(9)
2. Анализ влияния геометрических параметров на процесс деформирования с использованием полученных соотношений
1. Размер зоны интенсивного деформирования имеет порядок ширины зоны краевого эффекта в упругих оболочках (см. ф.(2),(7)).
2. Из формул (4) и (8) следует, что кольцевая цепная деформация для конической оболочки уменьшается с увеличением угла конусности, поскольку убывает безразмерная величина ![]() .
.

Рис.4. График функции ![]()
3. Для цилиндрической оболочки усилие деформирования постоянно (см. ф.(9)), однако деформации достаточно велики, например, для оболочки с ![]() кольцевая деформация равна
кольцевая деформация равна ![]() , что, видимо, превышает возможности деформирования металлических конструкционных материалов.
, что, видимо, превышает возможности деформирования металлических конструкционных материалов.
4. Для конической оболочки толщины ![]() с углом конусности
с углом конусности ![]() и радиусами ограничивающих окружностей 200 мм и 100 мм при максимальном перемещении 143 мм максимальная кольцевая деформация не превысит
и радиусами ограничивающих окружностей 200 мм и 100 мм при максимальном перемещении 143 мм максимальная кольцевая деформация не превысит ![]() , а усилие деформирования для материала с пределом текучести 200 Мпа при этим изменится от 94000 Н до 68000 Н. Таким образом, варьируя геометрические параметры оболочки, можно достичь достаточно низкой величины деформации материала при форме графика нагрузка – перемещение близкой к оптимальной прямоугольной.
, а усилие деформирования для материала с пределом текучести 200 Мпа при этим изменится от 94000 Н до 68000 Н. Таким образом, варьируя геометрические параметры оболочки, можно достичь достаточно низкой величины деформации материала при форме графика нагрузка – перемещение близкой к оптимальной прямоугольной.
Заключение
Разработана аналитическая модель деформирования конической оболочки, учитывающая геометрическую и физическую нелинейности. Получены зависимости для расчёта продольного усилия и кольцевой деформации в зависимости от геометрических параметров оболочки. С помощью полученных зависимостей установлено, что конические оболочки из металлических сплавов могут быть использованы в качестве энергопоглощающих элементов. Сопоставление расчётов по полученным формулам с результатами численных расчётов для нескольких конических оболочек показало удовлетворительное совпадение, что подтверждает возможность использования полученных соотношений для расчёта и анализа рассмотренного вида деформирования.
Список литературы
- Марков В.А., Пусев В.И., Селиванов В.В. О вопросах демпфирующих и амортизирующих свойств материалов и конструкций // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012. № 6. DOI: 10.7463/0612.0442023
- Петров Ю.А., Макаров В.П., Колобов А.Ю., Алешин В.Ф. Посадочные устройства космических аппаратов (КА) на основе пенопластов и сотоблоков // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2010. № 4. Режим доступа: http://technomag.edu.ru/doc/141542.html (дата обращения 18.08.2013).
- Погорелов А.В. Изгибания поверхностей и устойчивость оболочек. М.: Наука,1986. 96 с.
- Уваров А.И. Большие осесимметричные прогибы и устойчивость локально нагруженной оболочки вращения // Прикладная механика. 1987. Т. 33, № 3. С. 33-38.
- Уваров А.И. Пластические деформации оболочечных элементов конструктивной защиты // Судостроительная промышленность: научно-техн. сборник. Сер. Проектирование судов. Вып. 3. Ленинград: ЦНИИ "Румб”, 1986. С. 43-48.
- Фентон Дж. Несущий каркас кузова автомобиля и его расчет: пер. с англ. / под ред. Э.И. Григолюка. М.: Машиностроение, 1984. 200 с. [Fenton J. Vehicle Body Layout and Analysis. London: Mechanical Engineering LTD, 1980.].
- Малинин Н.Н. Прикладная теория пластичности и ползучести. М.: Машиностроение,1975. 400 с.
- Беленький Л.М. Большие деформации судовых конструкций. Л.: Судостроение, 1973. 208 с.
- Тимошенко С.П., Войновский-Кригер С. Пластинки и оболочки: пер. с англ. М.: Наука, 1966. 636 с. [Timoshenko S., Woinowsky-Krieger S. Theory Of Plates And Shells. New York, Toronto, London, McGraw Hill Company, Inc., 1959.]
Публикации с ключевыми словами: пластичность, оболочка, большие прогибы, ударный амортизатор
Публикации со словами: пластичность, оболочка, большие прогибы, ударный амортизатор
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



