научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#8 август 2007
Земнухов С.В., Мурзаханов Г.Х., Щугорев В.Н.
Московский
энергетический институт
(Технический университет), Россия
Для повышения надежности конструкций из композитных материалов необходимо разрабатывать методы расчета напряженно – деформированного состояния, учитывающие возникновение в конструкциях различных дефектов. Для осуществления такого учета нужны исследование различных видов разрушения и понимание того, как повреждения (например расслоения) влияют на поведение композита [1-3]. Актуальным является решение следующих задач: разработка моделей разрушения композитов; моделирование процессов разрушения композитов на ЭВМ; исследование дефектов типа расслоений в оболочках из композитных материалов при квазистатическом и циклическом нагружениях [4]; технологические задачи формирования крупногабаритных оболочек из композитных материалов; разработка метода расчета на прочность оболочек из композитных материалов, подкрепленных ребрами жесткости [5,6].
Многие широко применяемые на практике композиты имеют слоисто – волокнистую структуру. Низкая межслойная прочность делает конструкции из композитных материалов высоко чувствительными к дефектам типа расслоений. В дальнейшем композит слоисто – волокнистой структуры будем трактовать, как квазиизотропный однородный материал. Рассмотрим замкнутую сферическую оболочку из изотропного, упругого слоистого материала. Толщина оболочки Н, радиус кривизны R. Срединная поверхность отнесена к географической системе координат, причем угол q представляет собой угол долготы, j - угол широты. Вблизи внутренней или внешней поверхности оболочки имеется карманообразное эллипсоидальное отслоение толщиной h. Граница отслоения в декартовой системе координат на касательной плоскости описывается уравнением эллипса
![]()
где a и b – размеры полуосей эллипса, a,b<<R (см. рис. 1).
Оболочка подвергается всестороннему жесткому нагружению, так что там, где нет расслоения, радиальное перемещение всех точек срединной поверхности равно d. В процессе нагружения оболочки отслоение может увеличиваться в размерах как устойчиво так и не устойчиво, а также оно может выпучиваться.
Исследование карманообразного эллипсоидального отслоения проводилось при следующих предположениях:
1. До нагружения оболочки прогибы и усилия в срединной поверхности отсутствуют.
2. Оболочка тонкая H/R<<1, а стрела прогиба выпучившегося отслоения и его толщина малы по сравнению с толщиной оболочки и размерами эллипса h,f<<{H,a,b}.
3. Радиус оболочки R и минимальный радиус кривизны срединной поверхности отслоения таков, что по сравнению с ним размеры отслоения малы.
4. Тангенциальными перемещениями точек срединной поверхности выпучившегося отслоения можно пренебречь по сравнению с нормальными.
5. Поведение дефекта не влияет на напряженно-деформированное состояние монолитной части.

Рис. 1
Эллипсоидальное отслоение в сферической оболочке
Данные предположения позволяют рассматривать отслоение как пологую тонкую эллипсоидальную панель, защемленную по контуру и с заданным смещением на контуре.
Задачи устойчивости и роста отслоения в принципе нелинейны. Решение можно проводить путем интегрирования дифференциальных уравнений равновесия и вариационными методами. Однако, точного решения нелинейных дифференциальных уравнений найти, чаще всего невозможно, а их численное интегрирование трудоемко. Для определения обобщенных сил, продвигающих фронт дефекта, необходимо иметь выражение потенциальной энергии деформации в аналитическом виде как функцию размеров отслоения, и тогда численная минимизация функционала энергии по параметрам, характеризующим размеры дефекта, скорей всего может не понадобится. При исследовании роста отслоения необходимо многократно, для каждого значения угла qэ вычислять потенциальную энергию упругой деформации отслоения. При применении данных условий можно добиться решения задачи энергетическим методом.
Геометрическая особенность оболочки состоит в том, что при определенном закреплении ее краев она не допускает даже бесконечно малых чисто изгибных деформаций без растяжения-сжатия ее срединной поверхности. Нельзя деформировать эллипсоидальное отслоение жестко защемленное по краям, не вызывая удлинения срединной поверхности того же порядка что и прогибы отслоения.
Это приводит к тому, что формулы для критических нагрузок оболочек имеют более сложную структуру, чем формулы для критических нагрузок стержней и пластин: в них входят изгибная жесткость оболочки и жесткость на растяжение-сжатие. А также в результате этой особенности закритическое поведение оболочек качественно отличается от закритического поведения стержней и пластин вблизи критических точек бифуркации.
Для тонких упругих оболочек характерны два значения внешней нагрузки:
Р1 кр – верхняя критическая нагрузка, при превышении которой начальная форма равновесия идеально правильной оболочки перестает быть устойчивой;
Р2 кр – нижняя критическая нагрузка, при превышении которой становятся возможными новые, отличные от начального, состояния равновесия оболочки идеально правильной формы.
Воспользуемся энергетическим методом для нахождения критических значений нагрузки. В общем случае при действии внешней нагрузки в карманообразном отслоении возникают следующие нормальные усилия Nq и Nj, изгибающие Мq и Мj и крутящий Мqj моменты. Эти внутренние силовые факторы связаны с компонентами деформаций срединной поверхности эллипсоидального отслоения и изменением ее кривизн соотношениями упругости, основанными на гипотезах Кирхгофа-Лява:
 (1)
(1)
Критическое значение внешней нагрузки, при котором отслоение теряет устойчивость, найдем при следующих условиях:
- начальное напряженное состояние оболочки однородное и безмоментное, а отслоение имеет правильную сферическую форму;
- изменением всех геометрических размеров оболочки и отслоения в докритическом состоянии можно пренебречь;
- при потере устойчивости связь между перемещениями и внутренними силовыми факторами в отслоении описывается соотношениями упругости (1):
 (2)
(2)
где ![]() и
и ![]() - критические деформации
отслоения.
- критические деформации
отслоения.
Дополнительный прогиб выпучившегося отслоения срединной поверхности будем искать в виде
 (3)
(3)
где 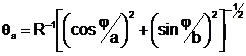 - значение угла q на контуре эллипсоидального отслоения; f³0 стрела
прогиба отслоения; k – коэффициент равный ±1 для отслоений на внутренней и наружной
поверхности
сферы отслоения соответственно.
- значение угла q на контуре эллипсоидального отслоения; f³0 стрела
прогиба отслоения; k – коэффициент равный ±1 для отслоений на внутренней и наружной
поверхности
сферы отслоения соответственно.
Для определения точек бифуркации необходимо найти условия существования новых состояний равновесия, смежных с исходными. Функция нормальных перемещений (3), описывающая изменение полной потенциальной энергии отслоения при переходе от начального безмоментного состояния равновесия к смежному, имеет следующий вид:
DЭ=Vb+Vc-W,
где Vb и Vc – изменение потенциальной энергии изгиба и сжатия эллипсоидального отслоения при переходе в выпученное состояние.
W – квадратичный функционал, зависящий от критических деформаций отслоения устойчивости.
Выражения для Vc, Vb, W при условии выполнения соотношения (2):
 (4)
(4)
Используя метод Ритца ![]() , получим соотношение,
связывающее критические деформации:
, получим соотношение,
связывающее критические деформации:
![]() (5)
(5)
Здесь введены следующие обозначения:
 (6)
(6)
Для
построения замкнутой системы уравнений относительно ![]() и
и ![]() , воспользуемся приемом, предложенным В.В.
Болотиным, который основан на осреднении деформаций по площади срединной
поверхности отслоения:
, воспользуемся приемом, предложенным В.В.
Болотиным, который основан на осреднении деформаций по площади срединной
поверхности отслоения:
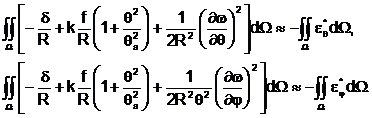 (7)
(7)
В левых частях стоят деформации eq и ef с учетом нелинейных членов, W - площадь эллипса, минусы в правых частях поставлены потому, что деформации сжатия приняты положительными. Соотношения (7) отражают физически оправданное предположение, что для выпучившегося отслоения с малой стрелой прогиба f << a,b соответствующие деформации близки к критическим.
Исключая критические деформации ![]() и
и ![]() из уравнений (5) - (7), получим следующее
уравнение относительно f:
из уравнений (5) - (7), получим следующее
уравнение относительно f:
![]() (9)
(9)
Здесь использованы обозначения
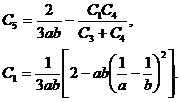
Обозначения остальных параметров приведены выше.
Решение уравнения (9) примет вид:
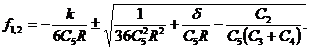 (10)
(10)
Несложный анализ показывает, что радикал по абсолютной величине больше первого члена, поэтому в выражении (10) следует брать только верхний знак, так как f – величина действительная и неотрицательная.
Для определения верхнего критического значения параметра внешней нагрузки d достаточно положить в уравнении (9) f=0. Тогда для отслоений выражения для значения верхней критической нагрузки, расположенных с внутренней и наружной стороны нагружаемой сферы соответственно примет вид:
![]() (11)
(11)
Задача
определения нижнего критического значения параметра внешней нагрузки ![]() сводится на данном этапе
к задаче нахождения минимума функции d=d(f) на полуинтервале f>0.
сводится на данном этапе
к задаче нахождения минимума функции d=d(f) на полуинтервале f>0.
Если отслоение расположено на внутренней поверхности сферы (k= -1), то критическое значение d можно найти из условия равенства
нулю дискриминанта уравнения (9) или из эквивалентного условия ![]() , где
, где ![]() - корень уравнения
- корень уравнения ![]() . Получим следующие
выражение
. Получим следующие
выражение
![]() .
(12)
.
(12)
Если отслоение расположено на внутренней поверхности сферы (k=1), то первый член выражения (12) отрицателен, а точка минимума функции d=d(f) находится в области f<0, что не удовлетворяет условию положительности f.
Критическое значение нагрузки dкр для отслоений, расположенных на внутренней и наружной поверхности оболочки:

Как и следовало ожидать, круговое отслоение, расположенное на внутренней поверхности оболочки, теряет устойчивость раньше, чем внешнее отслоение. При увеличении радиуса оболочки различие в критических значениях параметра внешней нагрузки уменьшается, а величина его стремится к h2/a2. Это совпадает с оценкой критической деформации для кругового отслоения, расположенного на плоской поверхности.
Зависимость стрелы прогиба эллипсоидального отслоения от
уровня внешней нагрузки показана на рис.2 . Графики функций ![]() для случая нагружения сферической
оболочки с эллипсоидальными отслоениями представлены на рис.2. Крестиками
помечены ветви 1’ и 2’, точки которых соответствуют
неустойчивым положениям равновесия отслоений. Из анализа следует, что закритическое
поведение эллипсоидальных отслоений, расположенных на внешней и внутренней
поверхностях квазистатически сжимаемой сферы, качественно различны. При
повышении критического значения внешней нагрузки стрела прогиба наружного отслоения
начинает монотонно увеличиваться (кривая 1). Критическое значение нагрузки для
внутреннего отслоения более низкое, а при превышении его переход на устойчивую
ветвь 2 возможен только скачком.
для случая нагружения сферической
оболочки с эллипсоидальными отслоениями представлены на рис.2. Крестиками
помечены ветви 1’ и 2’, точки которых соответствуют
неустойчивым положениям равновесия отслоений. Из анализа следует, что закритическое
поведение эллипсоидальных отслоений, расположенных на внешней и внутренней
поверхностях квазистатически сжимаемой сферы, качественно различны. При
повышении критического значения внешней нагрузки стрела прогиба наружного отслоения
начинает монотонно увеличиваться (кривая 1). Критическое значение нагрузки для
внутреннего отслоения более низкое, а при превышении его переход на устойчивую
ветвь 2 возможен только скачком.
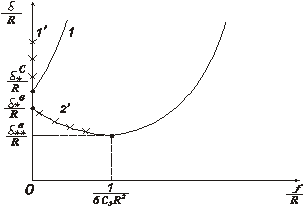
Рис. 2. Зависимость стрелы прогиба отслоения от уровня внешней нагрузки
Зависимость полного перемещения точки, расположенной в
вершине выпучившегося эллипсоидального отслоения (угол ![]() ), от уровня внешней нагрузки показана
на рис. 3. Предположим, что переход на устойчивую ветвь происходит непосредственно
в момент достижения критического значения нагрузки, тогда поведение точки,
принадлежащей внутреннему отслоению, описывается траекторией 0-1-2-3, а если точка
принадлежит внешнему отслоению, то 0-4-5. При учете различия в радиусах выпучившихся
слоев, расположенных на внутренних и внешних поверхностях оболочки, точки 4
и
), от уровня внешней нагрузки показана
на рис. 3. Предположим, что переход на устойчивую ветвь происходит непосредственно
в момент достижения критического значения нагрузки, тогда поведение точки,
принадлежащей внутреннему отслоению, описывается траекторией 0-1-2-3, а если точка
принадлежит внешнему отслоению, то 0-4-5. При учете различия в радиусах выпучившихся
слоев, расположенных на внутренних и внешних поверхностях оболочки, точки 4
и ![]() расходятся тем сильнее,
чем больше толщина оболочки
расходятся тем сильнее,
чем больше толщина оболочки ![]() .
.

Рис. 3. Зависимость полного
перемещения вершины выпучившегося эллипсоидального
отслоения (![]() ) от
уровня внешней нагрузки
) от
уровня внешней нагрузки
Равновесные размеры отслоений при квазистатическом нагружении
Для нахождения равновесных размеров разрастающегося в процессе нагружения отслоения вычислим потенциальную энергию упругой деформации отслоения как функцию размеров дефекта. Определим вначале потенциальную энергию сферической оболочки, нагруженной жестким радиальным смещением d, до выпучивания отслоения:
 .
.
Часть этой энергии сжатия накоплена не выпученным отслоением:
 .
.
При “жестком” нагружении оболочки смещением d>dкр отслоение выпучивается. Полные перемещения точек срединной поверхности отслоения можно записать в следующем виде
w=-d+k f (1-q2/qэ2 )2, (13)
а потенциальную энергию оболочки с выпучившимся отслоением описать с помощью функционала энергии
Э’=Vв+Vc+Vоб -Vотсл . (14)
Примем, что деформации сжатия в пределах выпучившегося отслоения постоянны и равны критическим, тогда
 .
(15)
.
(15)
Последние два члена выражения (14) описывают энергию сжатия оболочки без расслоения.
В случае “ жесткого” нагружения и пренебрежения диссипацией в материале тела, с помощью уравнения параметрической механики разрушения найдем выражения, описывающие обобщенные силы продвижения полуосей эллипсоидального двухпараметрического дефекта:
![]() и
и ![]() .
(16)
.
(16)
Выражение для прогиба
![]() (17)
(17)
Его производная будет соответственно равна
![]() .
(18)
.
(18)
Аналитические
значения для производных ![]() от
от ![]() и
и ![]() имеют вид:
имеют вид:
 (19)
(19)
Выражение для обобщенной силы Ga. Легко видеть, что выражение для Gb можно получить круговой заменой a«b, так как в (16) размеры a и b входят симметрично.
Равновесные размеры a и b найдем из уравнений многопараметрической механики разрушения:
![]() и
и ![]() ,
(20)
,
(20)
где ![]()
Геометрические
и физические параметры оболочки: ![]() Результаты расчетов представлены в
графической форме с использованием безразмерных переменных:
Результаты расчетов представлены в
графической форме с использованием безразмерных переменных: ![]() . Для указанных
параметров оболочки
. Для указанных
параметров оболочки ![]() .
.
На
рис. 4 изображены графики зависимости критических (семейство I) и равновесных размеров (II и III) круговых отслоений от уровня внешней нагрузки ![]() . Пусть на внутренней
(внешней) поверхности сферы имеется круговое отслоение радиусом а=40. Сфера
квазистатически нагружается радиальным обжатием
. Пусть на внутренней
(внешней) поверхности сферы имеется круговое отслоение радиусом а=40. Сфера
квазистатически нагружается радиальным обжатием ![]() . При
. При ![]() =1 произойдет выпучивание внутреннего
(внешнего) отслоения.
=1 произойдет выпучивание внутреннего
(внешнего) отслоения.
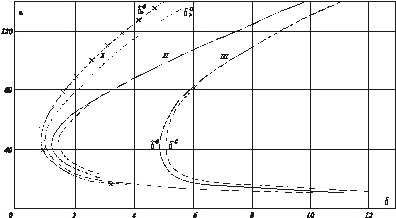
Рис. 4. Равновесные размеры круговых отслоений
Если материал оболочки таков, что ![]() (семейство кривых II), то при
(семейство кривых II), то при ![]() =1,3 начнется устойчивый рост
размеров отслоения. Если увеличить обобщенную силу сопротивления до величины
=1,3 начнется устойчивый рост
размеров отслоения. Если увеличить обобщенную силу сопротивления до величины ![]() (семейство III), то устойчивый рост размеров
отслоения начнется уже при
(семейство III), то устойчивый рост размеров
отслоения начнется уже при ![]() =4,8. Отметим, что выпучивание и рост внутреннего
отслоения начинается всегда раньше, чем внешнего.
=4,8. Отметим, что выпучивание и рост внутреннего
отслоения начинается всегда раньше, чем внешнего.
Возможен
и неустойчивый (скачкообразный) рост равновесного отслоения. Если ![]() и начальный размер
внутреннего отслоения а=20, то при
и начальный размер
внутреннего отслоения а=20, то при ![]() =3 произойдет неустойчивое (скачком) увеличение
размера до величины а=0,77, после чего с ростом
=3 произойдет неустойчивое (скачком) увеличение
размера до величины а=0,77, после чего с ростом ![]() будет наблюдаться устойчивый монотонный рост
а вдоль кривой II.
будет наблюдаться устойчивый монотонный рост
а вдоль кривой II.
На
рис. 5 и 6 показаны графики зависимости критических (штрихованные) и
равновесных (непрерывные кривые) размеров а эллипсоидальных внутренних и
наружных отслоений от уровня внешней нагрузки ![]() . Числа у кривых обозначают величину
параметра в. Зависимости равновесных размеров в от
. Числа у кривых обозначают величину
параметра в. Зависимости равновесных размеров в от ![]() при параметрическом
изменении а носят аналогичных характер. Это позволяет построить
поверхности критических и равновесных размеров в трехмерном пространстве (а,
в,
при параметрическом
изменении а носят аналогичных характер. Это позволяет построить
поверхности критических и равновесных размеров в трехмерном пространстве (а,
в, ![]() )
«нагрузка – параметры дефектов». На рис. 7 показан вариант таких
поверхностей
для эллипсоидальных внутренних отслоений, а на рис. 8 – характерные сечения
объемов, ограниченных рассматриваемыми поверхностями.
)
«нагрузка – параметры дефектов». На рис. 7 показан вариант таких
поверхностей
для эллипсоидальных внутренних отслоений, а на рис. 8 – характерные сечения
объемов, ограниченных рассматриваемыми поверхностями.

Рис. 5. Равновесные размеры эллипсоидальных отслоений
на внутренней поверхности сферы
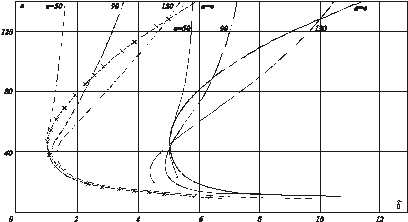
Рис. 6. Равновесные размеры эллипсоидальных отслоений
на внешней поверхности сферы
Точки 1-5 (рис. 7) принадлежат поверхности критических размеров, которую
можно задать с помощью скалярной функции ![]() . Отслоение с начальными параметрами
. Отслоение с начальными параметрами ![]() при возрастании внешней
нагрузки до величины
при возрастании внешней
нагрузки до величины ![]() достигают
равновесных размеров
достигают
равновесных размеров ![]() .
Вся внутренняя часть объёма призмы, ограниченная этой поверхностью,
соответствует области неравновесных размеров отслоения. Так как поверхность
является гладкой и неразрывной, то в каждой точке поверхности, описываемой с
помощью скалярной функции
.
Вся внутренняя часть объёма призмы, ограниченная этой поверхностью,
соответствует области неравновесных размеров отслоения. Так как поверхность
является гладкой и неразрывной, то в каждой точке поверхности, описываемой с
помощью скалярной функции ![]() , можно найти градиент этой функции
, можно найти градиент этой функции ![]() . Точки с отрицательным
градиентом (например, 6 и 10) соответствуют неустойчивым равновесным размерам
эллипсоидального отслоения. Точки, в которых градиент положителен (7,10), соответствуют
устойчивым равновесным размерам. При данном уровне нагружения, для круговых устойчивых
равновесных отслоений (точки 8, 9), величина градиента достигает максимума по
сравнению с градиентами во всех других точках, соответствующих эллипсоидальным
отслоениям.
. Точки с отрицательным
градиентом (например, 6 и 10) соответствуют неустойчивым равновесным размерам
эллипсоидального отслоения. Точки, в которых градиент положителен (7,10), соответствуют
устойчивым равновесным размерам. При данном уровне нагружения, для круговых устойчивых
равновесных отслоений (точки 8, 9), величина градиента достигает максимума по
сравнению с градиентами во всех других точках, соответствующих эллипсоидальным
отслоениям.

Рис. 7. Поверхности критических и равновесных размеров эллипсоидальных
отслоений на внутренней поверхности сферы
Обращая внимание на физическую сторону явления, отметим, что увеличение размеров кругового отслоения характеризуется максимальной скоростью высвобождения энергии упругой деформации. Поэтому, исходя из общих физических принципов, можно сделать вывод о том, что рост равновесного устойчивого эллипсоидального отслоения будет происходить таким образом, чтобы изображающая точка двигалась по поверхности равновесных размеров в направлении градиента. Следовательно, при квазистатическом нагружении форма эллипсоидального равновесного отслоения асимптотически стремится к круговой.

Рис. 8. Характерные сечения поверхностей критических и равновесных
размеров эллипсоидальных отслоений
На рис. 8
штриховкой справа – налево показаны области, все точки которых соответствуют
размерам отслоений, невыпученных при данном уровне нагрузок. Ограничивающие эти
области кривые соответствуют критическим размерам отслоений, выпучившихся при
данной нагрузке ![]() .
Области субравновесных отслоений не заштрихованы. Штриховкой слева – направо
обозначены области неравновесных размеров отслоений. Разграничивающие эти
области кривые соответствуют равновесным размерам отслоений. Устойчивость –
неустойчивость равновесных размеров контролируется знаком градиента F . При увеличении уровня внешней
нагрузки происходит уменьшение области субравновесных размеров и сближение
областей невыпучившихся и неравновесных отслоений.
.
Области субравновесных отслоений не заштрихованы. Штриховкой слева – направо
обозначены области неравновесных размеров отслоений. Разграничивающие эти
области кривые соответствуют равновесным размерам отслоений. Устойчивость –
неустойчивость равновесных размеров контролируется знаком градиента F . При увеличении уровня внешней
нагрузки происходит уменьшение области субравновесных размеров и сближение
областей невыпучившихся и неравновесных отслоений.
Литература
1. Болотин В. В. Дефекты типа расслоений в конструкциях из композитных материалов // Механика композитных материалов, 1984, № 2, с.. 239-255.
2. Болотин В. В. Межслойное разрушение композитов при комбинированном нагружении // Механика композитных материалов, 1988, № 3, с. 410-418.
3. Болотин В.В. О динамическом распространении трещин // Прикладная математика и механика,1992,т..56, вып. 1, с. 150-162.
4. Mursakhanov G. H., Shchugorev V.N. Destruction of dynamically loaded layered composite beams containing delaminations //Int. J. Eng. Dynamics, Strength, Wear – Resistance Machines, 1997, vol. 3, p.2-11.
5. Мурзаханов Г.Х., Щугорев В.Н. Разрушение композитов при низкоскоростном ударном нагружении. Ракетно-космическая техника. Фундаментальные и прикладные проблемы механики. Материалы международной научной конференции посвященной 90-летию В.И. Феодосьева. М.: МГТУ, 2006, с.60.
6. Земнухов С.В., Щугорев В.Н. Дефекты типа расслоения в изотропной упругой слоистой замкнутой сферической оболочке. // Материалы ХII международного симпозиума «Динамические и технологические проблемы механики конструкций и сплошных сред». Тезисы докладов, М.: МАИ, 2007, с. 127-128.
Публикации с ключевыми словами: композитные материалы, слоисто-волоконыне структуры, расчет нагрузки
Публикации со словами: композитные материалы, слоисто-волоконыне структуры, расчет нагрузки
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



