научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#4 апрель 2007
УДК 651.3:518.5
В.В.Сергеев
Введение
Достаточно важное направление изменений в тестовых методах оценивания подготовленности обучаемых связано с к компьютерным адаптивным тестированием, открывающим новые возможности для индивидуализации контрольно-корректировочных воздействий на обучаемого и реализации теоретических положений дистанционного обучения.
При измерении уровня знаний с неадаптивным тестированием для каждого обучаемого формируется тест определенной длины из выбранных случайным образом заданий тестового пространства. При этом тесты отличаются по сложности, и итоговая оценка формируется по числу правильных ответов с учетом весовых коэффициентов заданий. Недостатком такого тестирования может быть появление ситуаций, когда слабому студенту попадается сложный тест и как следствие этого – практическое отсутствие ответов. С другой стороны сильный студент может получить легкий тест и не реализовать свои способности. Для обеспечения максимальной информативности результатов контроля необходимо, чтобы средняя сложность предъявляемого обучаемому теста соответствовала его гипотетическому уровню обученности. Практически это можно осуществить с помощью адаптивного тестирования.
1. Понятие адаптивного тестирования и принципы его реализации.
Под адаптивным тестовым контролем понимают компьютеризованную систему научно обоснованной проверки и оценки результатов обучения, обладающую высокой эффективностью за счет оптимизации процедур генерации, предъявления и оценки результатов выполнения адаптивных тестов. Эффективность контрольно-оценочных процедур повышается при использовании многошаговой стратегии отбора и предъявления заданий, основанной на алгоритмах с полной контекстной зависимостью, в которых очередной шаг совершается только после оценки результатов выполнения предыдущего шага. После выполнения испытуемым очередного задания каждый раз возникает потребность в принятии решения о подборе трудности следующего задания в зависимости от того, верным или неверным был предыдущий ответ. Алгоритм отбора и предъявления заданий строится по принципу обратной связи, когда при правильном ответе испытуемого очередное задание выбирается более трудным, а неверный ответ влечет за собой предъявление последующего более легкого задания, чем то, на которое испытуемым был дан неверный ответ. К непременным условиям реализации таких алгоритмов следует отнести:
- наличие банка калиброванных заданий с устойчивыми оценками их параметров, позволяющими прогнозировать успех или неуспех испытуемого при подборе очередного задания адаптивного теста;
- использование программно-инструментальных средств и компьютерных программ для индивидуализации алгоритмов подбора заданий, основанных, как правило, на оценке вероятности правильного выполнения учебных заданий;
- использование параметрических моделей Item Response Theory.
Многошаговые стратегии адаптивного тестирования можно подразделить на фиксировано-ветвящиеся и варьирующие ветвящиеся в зависимости от того, как конструируются многошаговые адаптивные тесты. Если один и тот же набор с фиксированным расположением заданий на оси трудности используется для всех испытуемых, но каждый движется по набору индивидуальным путем в зависимости от результатов выполнения каждого очередного задания, то стратегия адаптивного тестирования является детерминировано (фиксировано) ветвящейся.
Варьирующая ветвящаяся стратегия адаптивного тестирования предполагает отбор заданий непосредственно из банка по определенным алгоритмам, которые прогнозируют оптимальную трудность последующего задания по результатам выполнения испытуемым предыдущего задания адаптивного теста. Отличительной особенностью варьирующей ветвящейся стратегии адаптивного тестирования является пошаговая переоценка уровня подготовленности испытуемого, предпринимаемая после каждого выполнения им очередного задания теста. Таким образом, появляется своеобразная последовательность текущих значений уровня подготовленности обучаемого, применительно к которым подбирается трудность заданий адаптивных тестов.
Сопоставление различных видов
адаптивного тестирования с позиции их эффективности для решения проблем
контроля в дистанционном образовании приводит к выбору компьютерного
адаптивного тестирования, основанного на многошаговых варьирующих стратегиях,
в качестве основного подхода. Наиболее важное преимущество варьирующих
стратегий связано с возможностью оперативного реагирования на результаты
выполнения учебных заданий путем переоценки уровня подготовленности обучаемого
после выполнения каждого очередного задания адаптивного теста. Последнее
обстоятельство порождает уникальные возможности в решении проблем
индивидуализации при обучении и контроле в дистанционном образовании.
2. Проблема объективной оценки подготовленности испытуемых.
Однако построить адекватную модель тестирования с привлечением только классической теории тестов сложно, так как уровень обученности (как измеряемый параметр) и трудность тестовых заданий (как параметр задания, устанавливаемый при его аттестации) имеют разные метрики.
Первичной информацией при тестировании знаний является набранный балл испытуемых или так называемый первичный балл. Достоинством этой оценки является ее простота и наглядность, Действительно, чем больше заданий выполнил испытуемый, тем выше его балл.
Однако проблема заключается в том, что первичный балл является не абсолютной, а относительной оценкой. Он существенно зависит от трудности заданий теста и на другом тесте он может оказаться иным, причем сама трудность теста в свою очередь определяется всем контингентом испытуемых. Желательно иметь объективную оценку уровня подготовленности испытуемых, подтверждаемую на различных тестах, имеющих заранее определенный уровень трудности заданий.
Вторым существенным недостатком первичных баллов является их нелинейность по отношению к тем параметрам, которые они должны характеризовать (уровень подготовленности). В частности, если тест состоит из 100 заданий, то разность в первичных баллах b1-b2=86-82=4 соответствует большему различию в уровне подготовленности участников, чем та же разность для участников имеющих, например 23 и 19 баллов. Сравнивая первичные баллы необходимо понимать, что первичные баллы являются лишь индикатором подготовленности испытуемых, а не ее мерой
Теория IRT позволяет установить связь между уровнем знаний испытуемых и результатами выполнения тестов, что позволяет определить уровень знаний независимо от сложности заданий. В качестве меры трудности заданий и меры уровня знаний применяется логит. Г.Раш ввел две меры: «логит уровня знаний» и «логит уровня трудности задания». Первую он определил как натуральный логарифм отношения доли правильных ответов испытуемого, на все задания теста, к доле неправильных ответов, а вторую – как натуральный логарифм другого отношения – доли неправильных ответов на задание теста к доле правильных ответов на тоже задание, по множеству испытуемых. Единая логарифмическая шкала позволяет установить требуемое соответствие между уровнем обученности и трудностью задания и, более того, произвести коррекцию результатов тестирования при тестах разной сложности.
В IRT вводится основное предположение о существовании некоторой взаимосвязи между наблюдаемыми результатами тестирования и латентными качествами испытуемых, выполняющих тест. Предполагается, что каждому испытуемому ставится в соответствие только одно значение латентного параметра. Элементы первого множества — это уровни знаний N испытуемых Θi, где i = 1,...,N. Второе множество образуют значения латентного параметра δj, j = 1,…, п, равные трудностям n заданий теста. На практике решается задача: по ответам испытуемых на задания теста оценить значения латентных параметров Θ и δ.
3. Применение модели Раша
3.1 Общее понятие о модели
Основной математической моделью IRT является однопараметрическая логистическая функция Раша, выражающая вероятность правильного ответа на задание j
![]()
Чем выше крутизна функции P, тем уже интервал, на котором это задание работает. Таким образом, возникла мысль об улучшении модели Раша за счет введения в выражение второго параметра аj. Параметр аj даёт информацию о задании с точки зрения оценки его дифференцирующей способности, на заданном интервале. Геометрически значение параметра аj выражается крутизной характеристической кривой, аналитически – значением производной функции в точке перегиба. После введения в выражение параметра аj получается двухпараметрическая модель педагогического измерения.
Возможно также добавление параметра C, определяющего вероятность угадывания правильного ответа.
Возникает проблема адекватной оценки трудности тестовых заданий и начального уровня знаний студентов. Начальная оценка уровня знаний испытуемого определяется по формуле Θi=ln(pi/qi), где pi – доля правильных ответов i-го испытуемого, qi – доля неправильных ответов, причем qi = 1 – pi. Аналогично определяется начальная оценка уровня трудности задания теста δj=ln(qj/pj), где pj – доля правильных ответов на j-е задание теста, qj – доля неправильных ответов.
В силу действия различных случайных факторов оценки параметров Θ и δ, полученные на нескольких выборках, будут, конечно, различаться. Если объем выборки достаточно велик, то можно ставить вопрос о вычислении устойчивых значений параметров Θ и δ, которые будут наиболее эффективными оценками и могут быть приняты в качестве объективных оценок параметров Θ и δ.
При любом проведении процесса тестирования результаты вычисления ![]() - статистических оценок
- статистических оценок ![]() , и δ- статистических
оценок δi будут отличаться от существующих точных значений. По
своему смыслу оценки являются определенными функциями исходных случайных
значений элементов матрицы ответов An,k состоящей из N- строк и
К
–столбцов и поэтому сами являются случайными величинами. Таким образом,
возникает вопрос о нахождении математических ожиданий и дисперсий этих
случайных величин. Необходимо чтобы математическое ожидание соответствующих
оценок совпадало с соответствующими точными значениями, а дисперсия оценки была
бы минимальной.
, и δ- статистических
оценок δi будут отличаться от существующих точных значений. По
своему смыслу оценки являются определенными функциями исходных случайных
значений элементов матрицы ответов An,k состоящей из N- строк и
К
–столбцов и поэтому сами являются случайными величинами. Таким образом,
возникает вопрос о нахождении математических ожиданий и дисперсий этих
случайных величин. Необходимо чтобы математическое ожидание соответствующих
оценок совпадало с соответствующими точными значениями, а дисперсия оценки была
бы минимальной.
Статистическая оценка уровня подготовленности и уровня трудности будут являться несмещенными оценками, если их математическое ожидание при любом объеме выборки испытуемых будет равно самому оцениваемому параметру. На практике обычно используют асимптотически несмещенную оценку, математическое ожидание которой стремится к истинному значению оцениваемого параметра, при неограниченном увеличении объема выборки.
Статистическая оценка эффективна если при заданной выборке, она имеет возможную наименьшую дисперсию D* при неполной информации, возможно, получить лишь оценку с D>D*. Если отношение D/D*→1, при увеличении выборки, то оценка называется асимптотически эффективной.
Статистическая оценка состоятельна, если несмещенная оценка не является эффективной, но при увеличении объема выборки ее дисперсия уменьшается.
Несмещенность, эффективность и состоятельность являются независимыми свойствами, характеризующими оценки с разных сторон. Задача отыскания эффективных несмещенных оценок имеет особо важное значение при обработке результатов малых выборок испытуемых.
Для получения оценки параметров δ и θ применяются метод моментов или метод наибольшего правдоподобия. Рассмотрим подробнее второй метод.
3.2. Получение начальной оценки уровня трудности заданий. Метод наибольшего правдоподобия
Данный
метод основывается на использовании функции правдоподобия. В применении к
тестированию функция правдоподобия L дискретной случайной величины балла aij
будет функцией аргументов ![]() и
и
![]() , представляющей
произведение вероятностей
, представляющей
произведение вероятностей  для
всевозможных значений i и j:
для
всевозможных значений i и j:

В
качестве точечных оценок латентных параметров принимают такие значения ![]() и
и ![]() , при которых функция правдоподобия
, при которых функция правдоподобия ![]() достигает максимума), такие оценки
называют оценками наибольшего правдоподобия). Необходимо отметить, что функции
достигает максимума), такие оценки
называют оценками наибольшего правдоподобия). Необходимо отметить, что функции
![]() и
и ![]() достигают максимума при одних и тех же значениях
своих аргументов, поэтому более удобно искать максимум функции
достигают максимума при одних и тех же значениях
своих аргументов, поэтому более удобно искать максимум функции ![]() . В данном случае:
. В данном случае:
![]() ,
,
где ![]() и
и ![]() - соответственно первичные баллы участников и
заданий.
- соответственно первичные баллы участников и
заданий.
Логарифмическая
функция правдоподобия зависит только от первичных баллов ![]() и
и ![]() , являющихся достаточными статистиками исходных
наблюдений. Для нахождения максимума функции правдоподобия приравняем нулю
частные производные логарифмической функции правдоподобия по каждому из
аргументов:
, являющихся достаточными статистиками исходных
наблюдений. Для нахождения максимума функции правдоподобия приравняем нулю
частные производные логарифмической функции правдоподобия по каждому из
аргументов:
 ,
i=1, 2, 3, ……N
,
i=1, 2, 3, ……N
 , j=1, 2, 3, ……K
, j=1, 2, 3, ……K
Данная
система нелинейных уравнений называется системой уравнений правдоподобия и
содержит (N+K) уравнений с (N+K) неизвестными латентными параметрами ![]() . Эта система имеет
единственное решение, соответствующее максимуму логарифмической функции
правдоподобия. В случае модели Раша наблюдается совпадение систем уравнений,
получаемых в методе моментов и методе максимального правдоподобия.
Следовательно, решение этих уравнений можно выполнить, используя все выше
изложенные рассуждения. Для другой функции успеха уравнения правдоподобия будут
иметь иной вид.
. Эта система имеет
единственное решение, соответствующее максимуму логарифмической функции
правдоподобия. В случае модели Раша наблюдается совпадение систем уравнений,
получаемых в методе моментов и методе максимального правдоподобия.
Следовательно, решение этих уравнений можно выполнить, используя все выше
изложенные рассуждения. Для другой функции успеха уравнения правдоподобия будут
иметь иной вид.
Метод наибольшего правдоподобия обладает следующими свойствами:
- Получаемые оценки являются состоятельными, несмещенными и эффективными.
- Оценки подчиняются нормальному распределению и имеют наименьшую дисперсию по сравнению с другими нормальными оценками.
- Если эффективные оценки существуют, то метод наибольшего правдоподобия дает именно эти оценки.
- Метод наибольшего правдоподобия наиболее полно использует данные выборки об оцениваемом параметре и позволяет найти достаточные оценки, если они существуют.
3.3. Перенос результатов тестирования различных выборок испытуемых на метрическую шкалу
Обычно в практике тестирования приходится использовать большое число параллельных тестов. В основном, это связанно с необходимостью защиты базы тестов от тиражирования правильных ответов среди участников тестирования. Однако в этом случае возникает необходимость сопоставления результатов, полученных по параллельным формам тестов, что является непростой задачей.
Рассмотрим
случай, когда N участников тестирования выполняют M различных вариантов теста,
состоящего из К заданий. Пусть ![]() участников выполняли задание
участников выполняли задание ![]() - го варианта. Таким образом, в
результате тестирования будет получено М различных матриц ответов
- го варианта. Таким образом, в
результате тестирования будет получено М различных матриц ответов ![]() , каждая из которых имеет размерность
, каждая из которых имеет размерность
![]() . Полученные результаты по
каждой из матриц ответов подчиняются однопараметрической модели Раша - в
результате математической обработки ответов могут быть получены оценки
латентных параметров трудности заданий
. Полученные результаты по
каждой из матриц ответов подчиняются однопараметрической модели Раша - в
результате математической обработки ответов могут быть получены оценки
латентных параметров трудности заданий ![]() и уровня подготовленности
и уровня подготовленности ![]() . Располагая полученными оценками,
необходимо выставить каждому i- участнику определенный окончательный балл
. Располагая полученными оценками,
необходимо выставить каждому i- участнику определенный окончательный балл ![]() , находящейся в интервале от 0
до 100, но при этом возникает ряд трудностей.
, находящейся в интервале от 0
до 100, но при этом возникает ряд трудностей.
Латентные
параметры трудности заданий ![]() и
уровней подготовленности участников
и
уровней подготовленности участников ![]() , полученные для каждого из вариантов, относятся к
метрическим, но не нормированным шкалам (можно измерить расстояния между
параметрами в логитах, но нельзя измерить расстояния параметров от начала
отсчета). Все отсчеты по таким шкалам можно сдвигать без потери информации. Для
сведения всех результатов к единой шкале необходимо перекрытие заданий (одни и
те же задания выполняют различные участники) или участников (одни и те же
участники выполняют различные задания) в различных вариантах теста. Рассмотрим
первый подход.
, полученные для каждого из вариантов, относятся к
метрическим, но не нормированным шкалам (можно измерить расстояния между
параметрами в логитах, но нельзя измерить расстояния параметров от начала
отсчета). Все отсчеты по таким шкалам можно сдвигать без потери информации. Для
сведения всех результатов к единой шкале необходимо перекрытие заданий (одни и
те же задания выполняют различные участники) или участников (одни и те же
участники выполняют различные задания) в различных вариантах теста. Рассмотрим
первый подход.
При
данном подходе все варианты тестов должны иметь общие задания (не менее 3) с
примерно одинаковым уровнем трудности, причем эти задания должны делить всю
шкалу трудности заданий примерно на равные интервалы. Подобные задания получили
название узловых (или якорных) заданий. Предположим, что у нас имеется три
одинаковых для всех вариантов теста задания с уровнями сложности ![]() ,
, ![]() и
и ![]() . Верхний индекс в круглых скобках определяет
взаиморасположение трудностей заданий. Для создания единой метрической шкалы по
всем вариантам теста необходимо с помощью критерия согласия проверить
статистические гипотезы о возможности применения модели Раша для описания
полученных экспериментальных результатов; задать условное начало (ноль)
метрической шкалы для всех вариантов, для чего из всех оценок латентных
параметров
. Верхний индекс в круглых скобках определяет
взаиморасположение трудностей заданий. Для создания единой метрической шкалы по
всем вариантам теста необходимо с помощью критерия согласия проверить
статистические гипотезы о возможности применения модели Раша для описания
полученных экспериментальных результатов; задать условное начало (ноль)
метрической шкалы для всех вариантов, для чего из всех оценок латентных
параметров ![]() и
и ![]() вычитается значение
вычитается значение ![]() ; усреднить трудности первого и
третьего узловых заданий, полученные по разным вариантам с учетом
соответствующих точностей (т.е. вычисляются средние весовые значения):
; усреднить трудности первого и
третьего узловых заданий, полученные по разным вариантам с учетом
соответствующих точностей (т.е. вычисляются средние весовые значения):
![]() ,
,
![]() ,
,
Здесь и ![]() - соответственно веса оценок
- соответственно веса оценок ![]() и
и ![]() , j- номер узловых заданий в вариантах теста,
, j- номер узловых заданий в вариантах теста, ![]() - номер варианта теста (от 1 до
М), С - произвольная константа.
- номер варианта теста (от 1 до
М), С - произвольная константа.
В конечном итоге трудностям узловых заданий приписывают следующие усредненные значения:
![]() ,
,
![]() ,
, ![]()
Исправленные
значения латентных параметров трудности заданий и уровня подготовленности,
испытуемых ![]() и
и ![]() , необходимые для перевода
результатов полученных по разным вариантам теста к единой метрической шкале
находят по следующим формулам:
, необходимые для перевода
результатов полученных по разным вариантам теста к единой метрической шкале
находят по следующим формулам:
если ![]() , то
, то 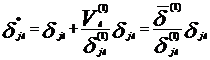 ;
;
если ![]() , то
, то  ;
;
если ![]() , то
, то  ;
;
если ![]() , то
, то 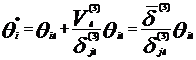 .
.
Используя исправленные значения уровней подготовленности участников тестирования, приведенные к единой метрической шкале можно определить их окончательный балл по формуле:
![]() ,
,
где ![]() - окончательный тестовый балл
на 100 бальной шкале,
- окончательный тестовый балл
на 100 бальной шкале, ![]() -
среднее значение исправленного уровня подготовленности,
-
среднее значение исправленного уровня подготовленности, ![]() - исправленный уровень подготовленности
i – участника,
- исправленный уровень подготовленности
i – участника, ![]() -
среднеквадратичное отклонение,
-
среднеквадратичное отклонение, ![]() - некоторые эмпирические коэффициенты подбираемые
вручную (например
- некоторые эмпирические коэффициенты подбираемые
вручную (например ![]() ,
, ![]() ).
).
4. Анализ качества теста
4.1 Показатели качества теста.
Одним из ключевых моментов диагностики знаний является необходимость не только оценивать уровень знаний испытуемых, но и анализировать качество диагностических материалов, что необходимо для адекватной оценки знаний.
Понятие качества диагностических материалов включает в себя оценку их надежности и валидности, являющихся одними из важнейших характеристик педагогических измерений. Валидность теста (его способность измерять именно те характеристики для измерения которых он был разработан) проверяется с помощью экспертной оценки. Надежность теста – это характеристика методики, отражающая точность измерения и устойчивость результатов к воздействию посторонних случайных факторов. При этом необходимо, чтобы сами испытуемые не изменяли свой уровень подготовки перед повторным тестированием (по тому же самому тесту). С одной стороны такая постановка вопроса является единственно верной, но с другой стороны желательно, чтобы испытуемый получал знания и в процессе тестирования (обучение на собственных ошибках) и анализируя свои результаты. Надежность теста связана с понятием стандартной ошибки, чем выше надежность, тем меньше стандартная ошибка измерений. Существует несколько различных понятий надежности диагностического теста и соответственно методов ее определения:
- надежность параллельных форм;
- ретестовая надежность;
- надежность расщепленных частей теста.
Надежность параллельных форм – характеристика, получаемая с помощью параллельных форм (вариантов) теста, проведенных на одной и той же выборке испытуемых. Корреляция результатов обоих тестов является показателем надежности. В реальной ситуации доказать параллельность двух форм (вариантов) теста или провести повторное тестирование с соблюдением одинаковых условий не представляется возможным.
Ретестовую надежность определяют при повторном использовании того же самого теста спустя некоторый промежуток времени. Однако, любой испытуемый, проходя тестирование, всегда получает дополнительные знания, анализируя свои результаты. Поэтому, ретестовая надежность так же не может считаться абсолютно объективным показателем.
Надежность расщепленных частей теста исследуется путем анализа устойчивости результатов отдельных совокупностей тестовых заданий при однократном тестировании. По сути, данный способ является некоторой модификацией способа исследования надежности параллельных форм, однако он более технологичен и поэтому получил более широкое распространение.
4.2 Оценка надежности теста
Для вычисления надежности теста как надежности параллельных форм используется коэффициент корреляции Пирсона между результатами двух параллельных тестов.
|
№ студента i |
Индивидуальный балл по тесту X |
Индивидуальный балл по тесту Y |
|
X2 |
Y2 |
|
1 |
X1 |
Y1 |
X1 Y1 |
X12 |
Y12 |
|
2 |
X2 |
Y2 |
X2 Y2 |
X22 |
Y22 |
|
….. |
….. |
…. |
…. |
…. |
…. |
|
N |
Xn |
Yn |
Xn Yn |
Xn2 |
Yn2 |
|
∑ |
∑Xi |
∑Yi |
∑ XiYi |
∑ Xi2 |
∑ Yi2 |

При оценке надежности теста по двум половинам расщепленного теста используется формула Спирмена-Брауна:
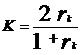 ,
,
где К -
надежность всего теста, а ![]() -
надежность, вычисленная по двум половинам теста, причем
-
надежность, вычисленная по двум половинам теста, причем ![]() вычисляется как коэффициент корреляции
Пирсона. При этом необходимо подсчитывать баллы испытуемых отдельно для четных
и для нечетных заданий теста
вычисляется как коэффициент корреляции
Пирсона. При этом необходимо подсчитывать баллы испытуемых отдельно для четных
и для нечетных заданий теста
|
№ студента i |
Индивидуальный балл по нечетным заданиям теста |
Индивидуальный балл по четным заданиям теста |
|
X2 |
Y2 |
|
1 |
X1 |
Y1 |
X1 Y1 |
X12 |
Y12 |
|
2 |
X2 |
Y2 |
X2 Y2 |
X22 |
Y22 |
|
….. |
….. |
…. |
…. |
…. |
…. |
|
N |
Xn |
Yn |
Xn Yn |
Xn2 |
Yn2 |
|
∑ |
∑Xi |
∑Yi |
∑ XiYi |
∑ Xi2 |
∑ Yi2 |
Если величина коэффициента надежности К составляет от 0,90 до 0,99, то тест имеет отличную оценку надежности, если от 0,80 до 0,89 то хорошую, от 0,70 до 0,79 – удовлетворительную и менее 0,69- неудовлетворительную надежность.
Заключение
К достоинствам рассмотренной в работе адаптивной модели тестирования можно отнести наличие непрерывной шкалы уровня подготовленности, что позволяет соотносить между собой результаты по различным тестам. Недостатком этой модели тестирования является необходимость в калибровке, т.е. в эмпирическом определении параметров заданий, требующем достаточно большого количества экспериментальных данных. Поэтому параметрические модели целесообразно применять при средне- и широкомасштабном нормативно-ориентированном тестировании.
Адаптивное тестирование в целом адекватно современным направлениям развития дистанционного образования и открывает новые возможности в повышении эффективности обучающих процессов.
Литература
1. Дистанционное обучение. Учебное пособие под ред Е.С. Полат. М.: Владос, 1998. – 192 с.
- Челышкова М. Б. Теория и практика конструирования педагогических тестов. – М.: Логос, 2002.- 410 с.
- Baker, F.B. The Basics of Item Response Theory. 2 ed. Hieneman, Portsmouth, New Hempshire, 2001. p. 7.
- Аванесов В.С. “Методологические и теоретические основы тестового педагогического контроля. Дисс. докт. пед. наук. С-Пб. Госуниверситет, 1994.- 339с.
- Нейман Ю.М., Хлебников В.А. Введение в теорию моделирования и параметризации педагогических тестов. - М.: Прометей, 2000, - 168 С.
6. Герасимович А.И., Матвеева Я.И. Математическая статистика. – Минск.: Высшая школа, 1978. – 200 .
- Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1997, -480 С.
- Feltd S.N.,
Brennan, R.L. Reliability In R.L. Linn. Educational measurement (3rd ed.) New
York, Macmillan, 1989,
pp.105-146.
Публикации с ключевыми словами: дистанционное обучение
Публикации со словами: дистанционное обучение
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



