научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2013
DOI: 10.7463/1113.0645575
УДК 629.1.028
Россия, МГТУ им. Н.Э. Баумана
Введение
Одним из характерных условий эксплуатации армейских колесных машин (КМ) является движение в составе колонны. При некоторых обстоятельствах (террористические акты, неисправности технического характера, возникающие у машин и др.) требуется объезд впереди стоящих транспортных средств, в том числе, движение через придорожный кювет, въезд на насыпь, переезд траншеи.
Важной составляющей в общей модели КМ [1-4], определяющей нагрузки в трансмиссии, является модель взаимодействия шины с неровной поверхностью дороги. В работах [5, 6] рассмотрены конечно-элементные, а в работах [7, 8] с распределенным контактом модели взаимодействия шины с неровностями, которые требуют для расчета значительного числа экспериментальных данных.
При движении через неровности, описываемые гладкими функциями, вполне адекватные результаты можно получить, если использовать модель шины с точечным контактом с опорной поверхностью [1]. Недостатком этой модели является задание перемещения колес в системе координат, жестко связанной с опорной поверхностью, в то время как в действительности колеса перемещаются относительно корпуса машины.
В соответствии с этим, целью настоящей работы является получение дифференциальных уравнений динамической системы КМ при ее движении по твердой неровной поверхности, которые бы более точно отражали действительные физические процессы, происходящие в динамической системе трансмиссии и системе подрессоривания при рассматриваемом нагружении.
Научной новизной работы является математическая модель движения полноприводной колесной машины по дороге с твердой неровной поверхностью, позволяющая существенно уточнить нагрузки, возникающие в системах трансмиссии и подрессоривания КМ в реальных условиях ее эксплуатации.
Вывод уравнений движения
Рассмотрим методику создания математической модели для расчета нагруженности трансмиссии, исключив недостаток, отмеченный в работе [1].
Примем следующие допущения:
– машина считается системой твердых тел, шарнирно или упруго связанных между собой;
– корпус машины и её рама, если таковая имеется, являются абсолютно жесткими;
– подвеска всех колес независимая на поперечных рычагах;
– двигатель и корпуса агрегатов трансмиссии, кроме колесных редукторов, жестко закреплены на корпусе машины;
– контакт колеса с дорогой точечный;
– колебания тел считаются малыми;![]()
– качение колеса по дороге происходит без скольжения;
– движение КМ происходит в направлении оси ![]() системы координат
системы координат ![]() XYZ, связанной с опорной поверхностью, при отсутствии отрыва колес от дороги, профиль которой задан уравнением (рис.1)
XYZ, связанной с опорной поверхностью, при отсутствии отрыва колес от дороги, профиль которой задан уравнением (рис.1)
![]() ,
,
где ![]() ,
, ![]() -- координаты произвольной точки на поверхности дороги,
-- координаты произвольной точки на поверхности дороги, ![]() и
и ![]() – период и амплитуда функции, характеризующей синусоидальные волны на поверхности дороги (движение КМ происходит не перпендикулярно прямолинейной образующей поверхности дороги, а под некоторым углом 90o
– период и амплитуда функции, характеризующей синусоидальные волны на поверхности дороги (движение КМ происходит не перпендикулярно прямолинейной образующей поверхности дороги, а под некоторым углом 90o![]() к ней).
к ней).

Рис. 1. Схема колесной машины в системе координат ![]() XYZ, связанной с опорной поверхностью
XYZ, связанной с опорной поверхностью
Представим нашу динамическую систему как систему следующих твердых тел: корпус колесной машины с центром инерции в точке О, обладающий массой ![]() и моментами инерции
и моментами инерции ![]() относительно главных центральных осей корпуса
относительно главных центральных осей корпуса ![]() соответственно; массы трансмиссии с моментами инерции
соответственно; массы трансмиссии с моментами инерции ![]() относительно своих осей вращения, проходящих через точки
относительно своих осей вращения, проходящих через точки ![]() ,
, ![]() =1, 2,…,
=1, 2,…,![]() ; массы колес
; массы колес ![]() , сосредоточенные в центрах колес – точках
, сосредоточенные в центрах колес – точках ![]() ,
, ![]() =1, 2,…,2
=1, 2,…,2![]() , где
, где ![]() - число осей колесной машины. Точка
- число осей колесной машины. Точка ![]() – точка пересечения оси вращения
– точка пересечения оси вращения ![]() - го колеса с плоскостью продольной симметрии последнего.
- го колеса с плоскостью продольной симметрии последнего.
Для описания движения системы вводятся следующие обобщенные координаты: ![]() – линейные координаты точки
– линейные координаты точки ![]() в системе осей
в системе осей ![]() XYZ;
XYZ; ![]() - углы поворота корпуса машины;
- углы поворота корпуса машины; ![]() - углы поворота масс трансмиссии вокруг собственных осей вращения;
- углы поворота масс трансмиссии вокруг собственных осей вращения; ![]() - вертикальные координаты точек
- вертикальные координаты точек ![]() в системе координат
в системе координат ![]() (в направлении оси
(в направлении оси ![]() ). Координаты
). Координаты ![]() и
и ![]() отсчитываются от положения статического равновесия колесной машины на горизонтальной плоскости.
отсчитываются от положения статического равновесия колесной машины на горизонтальной плоскости.
Для упрощения уравнений движения, динамическая система трансмиссии предварительно приведена к валу колеса, для чего моменты инерции ![]() и коэффициенты жесткости упругих связей масс трансмиссии разделены на квадраты передаточных чисел от соответствующего вала до колеса.
и коэффициенты жесткости упругих связей масс трансмиссии разделены на квадраты передаточных чисел от соответствующего вала до колеса.
Движение рассматриваемой динамической системы может быть описано дифференциальными уравнениями Лагранжа второго рода
 , к = 1,2,…,
, к = 1,2,…,![]() ,
,
где Т, П – кинетическая и потенциальная энергии системы; Ф – диссипативная функция; ![]() – обобщенная сила, соответствующая обобщенной координате
– обобщенная сила, соответствующая обобщенной координате ![]() ;
; ![]() - число обобщенных координат:
- число обобщенных координат:
![]() = 6 +
= 6 + ![]() + 2
+ 2![]() .
.
Для написания выражений Т, П и Ф в точке О введем кроме системы координат ![]() , оси которой направлены вдоль главных центральных осей инерции корпуса, еще две системы координат:
, оси которой направлены вдоль главных центральных осей инерции корпуса, еще две системы координат: ![]() , совпадающую в начальный момент времени t = 0 c системой координат
, совпадающую в начальный момент времени t = 0 c системой координат ![]() ;
; ![]() , оси которой параллельны соответствующим осям системы координат
, оси которой параллельны соответствующим осям системы координат ![]() XYZ.
XYZ.
Переход от системы координат ![]() к системе
к системе ![]() [9] задается с помощью трех последовательных поворотов (рис. 2). Первый поворот – поворот плоскости
[9] задается с помощью трех последовательных поворотов (рис. 2). Первый поворот – поворот плоскости ![]() вокруг оси
вокруг оси ![]() на угол
на угол ![]() - угол продольного крена, в результате которого ось
- угол продольного крена, в результате которого ось ![]() займет положение ОN, a
займет положение ОN, a ![]() -
- ![]() . Второй поворот – поворот плоскости
. Второй поворот – поворот плоскости ![]() вокруг линии узлов ON на угол
вокруг линии узлов ON на угол ![]() - угол поперечного крена, в результате которого ось
- угол поперечного крена, в результате которого ось ![]() займет положение
займет положение ![]() , а
, а ![]() –
– ![]() . Третий поворот – поворот плоскости
. Третий поворот – поворот плоскости ![]() вокруг оси
вокруг оси ![]() на угол
на угол ![]() – угол рысканья, в результате которого ось ON займет положение
– угол рысканья, в результате которого ось ON займет положение ![]() , а
, а ![]() –
– ![]() .
.
Взаимное положение осей систем координат ![]() и
и ![]() может быть задано с помощью таблицы косинусов углов между соответствующими осями координат, которая с учетом малости углов
может быть задано с помощью таблицы косинусов углов между соответствующими осями координат, которая с учетом малости углов ![]() ,
, ![]() ,
, ![]() может быть представлена в виде табл. 1.
может быть представлена в виде табл. 1.

Рис. 2. Углы между системами координат ![]() и
и ![]()
Таблица 1. Косинусы углов между осями систем координат ![]() и
и ![]()
|
|
|
|
| 1 |
| - |
|
| 1 |
|
|
| - | 1 |
Этой таблице косинусов может быть поставлено в соответствие матричное равенство [10]
![]() , (1)
, (1)
где ![]() - матрица-столбец, элементами которой являются координаты какой-либо точки S в системе координат O
- матрица-столбец, элементами которой являются координаты какой-либо точки S в системе координат O![]() ;
; ![]() – матрица-столбец, элементами которой являются координаты той же точки S в системе координат
– матрица-столбец, элементами которой являются координаты той же точки S в системе координат ![]() ;
; ![]() - квадратная матрица размерности 3х3:
- квадратная матрица размерности 3х3:
 . (2)
. (2)
Равенство (1) дает нам возможность определить координаты точки в системе координат О![]() , зная ее координаты в системе
, зная ее координаты в системе ![]() .
.
Аналогичным образом вводим углы между осями систем координат ![]() и
и ![]() , и получаем матричное равенство
, и получаем матричное равенство
![]()
![]() , (3)
, (3)
где ![]() - матрица-столбец, элементами которой являются координаты той же точки S в системе координат
- матрица-столбец, элементами которой являются координаты той же точки S в системе координат ![]() ;
; ![]() -квадратная матрица размерности 3х3, элементами которой являются
-квадратная матрица размерности 3х3, элементами которой являются ![]() косинусы углов между соответствующими осями систем координат
косинусы углов между соответствующими осями систем координат ![]() и
и ![]() .
.
Так как в процессе движения положение систем координат ![]() и
и ![]() не меняется, то все элементы матрицы
не меняется, то все элементы матрицы ![]() являются постоянными числами, зависящими только от взаимного положения систем координат
являются постоянными числами, зависящими только от взаимного положения систем координат ![]() и
и ![]() XYZ в начальный момент времени t = 0. С учетом выражений (1) и (3) можно записать
XYZ в начальный момент времени t = 0. С учетом выражений (1) и (3) можно записать
![]() , (4)
, (4)
где ![]() .
.
Матрицы ![]() и
и ![]() являются ортогональными, так как они составлены из элементов таблиц косинусов. Для таких матриц обратная матрица является транспонированной, то есть
являются ортогональными, так как они составлены из элементов таблиц косинусов. Для таких матриц обратная матрица является транспонированной, то есть ![]() =
= ![]() .
. ![]()
![]()
![]()
![]() Тогда выражение (4) может быть переписано в виде
Тогда выражение (4) может быть переписано в виде
![]() .
. ![]() .
. ![]() . (5)
. (5)
С учетом обозначений, введенных на рис. 2 (![]() ), выражение для мгновенной угловой скорости системы координат
), выражение для мгновенной угловой скорости системы координат ![]() (корпуса машины) по отношению к системе координат
(корпуса машины) по отношению к системе координат ![]() и, следовательно, к системе
и, следовательно, к системе ![]() XYZ , может быть записано в виде
XYZ , может быть записано в виде
![]() .
.
Если обозначить через ![]() ,
, ![]() ,
, ![]() - проекции мгновенной угловой скорости
- проекции мгновенной угловой скорости ![]() на оси системы координат
на оси системы координат ![]() , неразрывно связанные с корпусом колесной машины, то с учетом малости колебаний имеем
, неразрывно связанные с корпусом колесной машины, то с учетом малости колебаний имеем ![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]() .
.
Потенциальная энергия системы состоит из потенциальных энергий трансмиссии Птр, подвески Пп и шин Пш:
П = Птр + Пп + Пш;

Здесь ![]() - коэффициенты жесткости упругих связей между
- коэффициенты жесткости упругих связей между ![]() и
и ![]() массами трансмиссии;
массами трансмиссии;
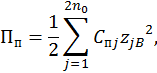
где ![]() - коэффициент жесткости подвески j-го колеса в направлении координаты
- коэффициент жесткости подвески j-го колеса в направлении координаты ![]() , приведенный к перемещению центра
, приведенный к перемещению центра ![]() j-го колеса;
j-го колеса;

где ![]() - коэффициент жесткости шины j-го колеса в радиальном направлении;
- коэффициент жесткости шины j-го колеса в радиальном направлении; ![]() - вертикальная координата (в системе
- вертикальная координата (в системе ![]() XYZ) дороги под центром обода
XYZ) дороги под центром обода ![]() j-го колеса (она меняется от –
j-го колеса (она меняется от – ![]() до +
до + ![]() );
); ![]() - вертикальная проекция (в системе
- вертикальная проекция (в системе ![]() XYZ) центра обода
XYZ) центра обода ![]() j-го колеса относительно положения статического равновесия КМ на горизонтальной плоскости;
j-го колеса относительно положения статического равновесия КМ на горизонтальной плоскости;
![]() .
.
Для определения ![]() введем точку
введем точку ![]() (рис. 3), под которой понимается точка, неподвижно связанная с корпусом КМ, совпадающая с центром обода
(рис. 3), под которой понимается точка, неподвижно связанная с корпусом КМ, совпадающая с центром обода ![]() j-го колеса в начальном (статическом) положении КМ на горизонтальной плоскости.
j-го колеса в начальном (статическом) положении КМ на горизонтальной плоскости.
Неизменные координаты точки ![]() в системе
в системе ![]() обозначим через
обозначим через ![]() Радиус-вектору
Радиус-вектору ![]() точки
точки ![]() в системе координат
в системе координат ![]() поставим в соответствие матрицу-столбец
поставим в соответствие матрицу-столбец
 .
.
Тогда
![]()
где ![]() oj – матрица-столбец с координатами точки
oj – матрица-столбец с координатами точки ![]() в системе координат
в системе координат ![]() XYZ;
XYZ; ![]() - матрица-столбец
- матрица-столбец ![]() в начальном (статическом) положении колесной машины на горизонтальной плоскости.
в начальном (статическом) положении колесной машины на горизонтальной плоскости.
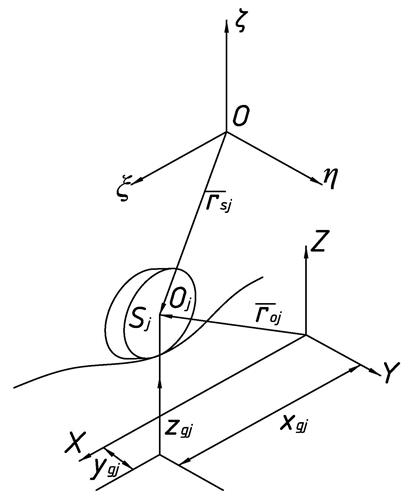
Рис. 3. Координаты центра колеса в системах координат ![]() и
и ![]() XYZ
XYZ
Обозначим ![]() oj– радиус-вектор точки
oj– радиус-вектор точки ![]() в системе координат
в системе координат ![]() XYZ. Тогда
XYZ. Тогда
![]() ,
,
где ![]() o - радиус-вектор точки
o - радиус-вектор точки ![]() в системе
в системе ![]() XYZ;
XYZ; ![]() - радиус-вектор с началом в точке
- радиус-вектор с началом в точке ![]() , а концом в точке
, а концом в точке ![]() в системе
в системе ![]() .
.
По аналогии с выражением (5) последнее векторное равенство в системе координат ![]() XYZ примет вид
XYZ примет вид
![]()
где ![]()
![]() - вертикальная координата точки
- вертикальная координата точки ![]() в статическом положении КМ на горизонтальной плоскости в системе
в статическом положении КМ на горизонтальной плоскости в системе ![]() XYZ;
XYZ; ![]() sjoj - матрица-столбец с координатами вектора
sjoj - матрица-столбец с координатами вектора ![]() sjoj в системе координат
sjoj в системе координат ![]() ;
;
![]()
![]()
Итак,


Примем, что в начальный момент t= 0 КМ находится в статическом положении на горизонтальной плоскости, так что ![]() (также как и
(также как и ![]() ).
).
Тогда

Координаты (в системе ![]() XYZ) перемещения точки
XYZ) перемещения точки ![]() относительно положения статического равновесия КМ на горизонтальной плоскости найдутся из выражения
относительно положения статического равновесия КМ на горизонтальной плоскости найдутся из выражения

Если в первом приближении считать, что главные центральные оси ![]() КМ совпадают с осями симметрии КМ и в начальный момент движения (в статическом положении КМ на горизонтальной плоскости) параллельны осям системы
КМ совпадают с осями симметрии КМ и в начальный момент движения (в статическом положении КМ на горизонтальной плоскости) параллельны осям системы ![]() , то
, то

и последнее равенство перепишется в виде

В результате
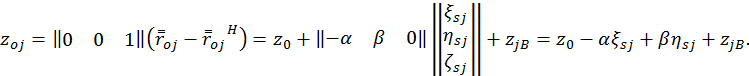
Координаты ![]() точки
точки ![]() можно вычислить по формуле:
можно вычислить по формуле:

или с учетом ![]() =
=![]() – по формуле
– по формуле

Аналогично для ![]() имеем выражение
имеем выражение

В результате вертикальная координата дороги над точкой ![]() запишется в виде
запишется в виде

а потенциальная энергия шины примет вид

Кинетическая энергия системы в первом приближении может быть представлена в виде суммы кинетических энергий корпуса колесной машины ![]() , вращающихся масс трансмиссии
, вращающихся масс трансмиссии ![]() и поступательно движущихся масс колес
и поступательно движущихся масс колес ![]() :
:
![]() =
=![]() +
+![]() +
+![]() ;
;
![]()


Здесь ![]() – абсолютная скорость точки
– абсолютная скорость точки ![]() (в системе
(в системе ![]() XYZ).
XYZ).
![]() ,
,
где ![]() – скорость точки
– скорость точки ![]() относительно системы координат
относительно системы координат ![]() ;
;
![]() - скорость той точки системы координат
- скорость той точки системы координат ![]() , с которой в данный момент совпадает точка
, с которой в данный момент совпадает точка ![]() , относительно системы
, относительно системы ![]() ;
;
![]() - скорость той точки системы координат
- скорость той точки системы координат ![]() , с которой в данный момент совпадает точка
, с которой в данный момент совпадает точка ![]() , относительно системы
, относительно системы ![]() ;
;
![]() - скорость той точки системы координат
- скорость той точки системы координат ![]() , с которой в данный момент совпадает точка
, с которой в данный момент совпадает точка ![]() ,относительно системы
,относительно системы ![]() XYZ.
XYZ.
По условию введения систем координат скорость ![]() (так как система
(так как система ![]() неподвижна относительно системы
неподвижна относительно системы ![]() ). Чтобы сложить векторы в последнем равенстве, необходимо выразить их через проекции в какой-нибудь одной системе координат, например в системе
). Чтобы сложить векторы в последнем равенстве, необходимо выразить их через проекции в какой-нибудь одной системе координат, например в системе ![]() :
:
![]() .
.
Здесь элементами всех введенных матриц-столбцов являются проекции одноименных векторов на оси системы координат ![]() XYZ.
XYZ.
Точка ![]() в системе
в системе ![]() задается матрицей-столбцом
задается матрицей-столбцом
![]() sjoj
sjoj а
а 
Так как ![]()
Чтобы спроектировать вектор ![]() на оси
на оси ![]() , необходимо умножить матрицу-столбец
, необходимо умножить матрицу-столбец ![]() слева на матрицу
слева на матрицу ![]() :
:
![]()
Точка ![]() имеет в системе
имеет в системе ![]() радиус вектор
радиус вектор ![]() с координатами
с координатами ![]()
![]() Сама система
Сама система ![]() поворачивается относительно системы
поворачивается относительно системы ![]() с мгновенной угловой скоростью
с мгновенной угловой скоростью ![]() , имеющей проекции
, имеющей проекции ![]() на оси
на оси ![]() Тогда по формуле Эйлера имеем
Тогда по формуле Эйлера имеем
![]() .
.
Здесь координаты вектора ![]() являются его проекциями в системе
являются его проекциями в системе![]() .
.
Векторному произведению ![]() можно сопоставить произведение двух матриц
можно сопоставить произведение двух матриц ![]() – вектор-столбец. Чтобы спроецировать этот вектор на оси системы
– вектор-столбец. Чтобы спроецировать этот вектор на оси системы ![]() нужно умножить это произведение слева на матрицу
нужно умножить это произведение слева на матрицу ![]() В результате получим
В результате получим
![]()
где 
И, наконец, ![]() .
.
В итоге получаем
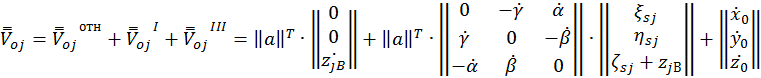
или
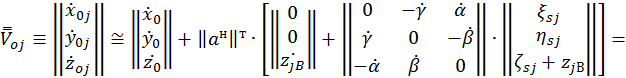

 .
.
С учетом малости обобщенных координат и их скоростей имеем
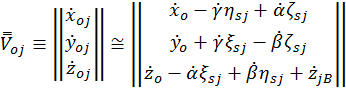 .
.
В результате, поскольку
![]() ,
,
окончательно получим
![]() .
.
При вычислении диссипативной функции в первом приближении могут быть учтены только потери энергии в подвеске. Тогда

где ![]() – коэффициент трения в амортизаторе j-го колеса, приведенный к перемещению центра колеса (точки
– коэффициент трения в амортизаторе j-го колеса, приведенный к перемещению центра колеса (точки ![]() ).
).
В качестве обобщенной силы, действующей на координату ![]() , cчитаем приведенный к колесу крутящий момент двигателя, который, в частности, для дизеля может быть задан как совокупность внешней и регулярных характеристик (рис. 4):
, cчитаем приведенный к колесу крутящий момент двигателя, который, в частности, для дизеля может быть задан как совокупность внешней и регулярных характеристик (рис. 4):
![]()
Здесь ![]() – суммарное передаточное число от двигателя до колеса.
– суммарное передаточное число от двигателя до колеса.
Считая в первом приближении радиусы качения колес постоянными, уравнение связи колес с дорогой представим в виде
![]()
Таким образом, углы поворота колес ![]() при данной постановке задачи не будут являться обобщенными координатами, а будут зависеть от обобщенной координаты
при данной постановке задачи не будут являться обобщенными координатами, а будут зависеть от обобщенной координаты ![]() .
.
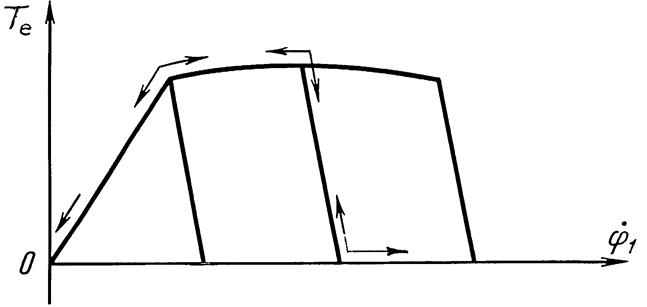
Рис. 4. Внешняя и регуляторные характеристики дизеля
Обобщенная сила ![]() по координате
по координате ![]() обусловлена силами сопротивления воздуха, качения колес по дороге и подъема колес по неровности:
обусловлена силами сопротивления воздуха, качения колес по дороге и подъема колес по неровности:

Здесь f – коэффициент сопротивления качению колеса; ![]() – угол наклона касательной к поверхности дороги в плоскости, перпендикулярной плоскости
– угол наклона касательной к поверхности дороги в плоскости, перпендикулярной плоскости ![]() в точке дороги, лежащей под центром
в точке дороги, лежащей под центром ![]() j-го колеса;
j-го колеса; ![]() – вертикальная сила в контакте j-го колеса с дорогой:
– вертикальная сила в контакте j-го колеса с дорогой:
![]()
где ![]() – статический прогиб шины;
– статический прогиб шины;
![]() ;
;
![]() – коэффициент обтекаемости;
– коэффициент обтекаемости;
![]() – коэффициент заполнения площади лобового сечения КМ;
– коэффициент заполнения площади лобового сечения КМ;
B и H – колея и габаритная высота машины соответственно;
![]() – плотность воздуха.
– плотность воздуха.
Остальные обобщенные силы считаем равными нулю.
Подставляя все найденные выражения для Т, П, Ф и Q в уравнения Лагранжа второго рода, получим систему дифференциальных уравнений, записанную в матричной форме:
![]()
Здесь ![]() – квадратные матрицы порядка nк х nк, элементы которых являются постоянными величинами;
– квадратные матрицы порядка nк х nк, элементы которых являются постоянными величинами; ![]() – матрица-столбец обобщенных координат
– матрица-столбец обобщенных координат ![]() порядка nк;
порядка nк; ![]() - матрица-столбец порядка nк, элементами которой являются нелинейные функции обобщенных координат и их производных.
- матрица-столбец порядка nк, элементами которой являются нелинейные функции обобщенных координат и их производных.
Решение последней системы дифференциальных уравнений позволяет определить все обобщенные координаты и скорости в функции времени и вычислить текущее значение упругого момента на участке трансмиссии между i-ой и k-ой массами
![]()
при движении колесной машины по дороге с определенными параметрами ![]() и
и ![]() .
.
Одновременно может быть вычислена нагрузка на j-ое колесо со стороны дороги
![]()
и в первом приближении – нагрузка на корпус КМ со стороны системы подрессоривания
![]() ,
,
где ![]() – статический прогиб системы подрессоривания j– ого колеса.
– статический прогиб системы подрессоривания j– ого колеса.
Заключение
Задание перемещений колес в системе координат, связанной с корпусом колесной машины, позволяет по сравнению с математической моделью, использованной в работе [1], существенно уточнить выражения для потенциальной, кинетической энергий и диссипативной функции системы, что, в конечном счете, обеспечивает адекватность математическую модель движения полноприводной колесной машины по твердой неровной поверхности дороги.
Разработанная математическая модель взаимосвязанной динамической системы многоосной полноприводной КМ дает возможность достоверно оценить динамическую нагруженность деталей трансмиссии и системы подрессоривания при неустановившемся движении машины в условиях совместного нагружения от двигателя и несимметричного пространственного нагружения от дорожной поверхности.
Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках договора №9905/17/07-к-12 между ОАО «КАМАЗ» и «Московским государственным техническим университетом имени Н.Э. Баумана».
Список литературы
1. Полунгян А.А., Фоминых А.Б. Математическая модель динамики трансмиссии колесной машины при движении по твердой неровной дороге // Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2003. № 4. С. 15-25.
2. Белоусов Б.Н., Шухман С.Б. Прикладная механика наземных тягово-транспортных средств с мехатронными системами: монография / под общ. ред. докт. техн. наук, проф. Б.Н. Белоусова. М.: Агроконсалт, 2013. 612 с.
3. Белоусов Б.Н., Попов С.Д. Колесные транспортные средства особо большой грузоподъемности. Конструкция. Теория. Расчет / Под общ. ред. Б.Н. Белоусова. М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. 728 с.
4. Камаль А., Фоминых А.Б. Математическая модель движения по ровной дороге двухосной полноприводной колесной машины с вариаторами в раздаточной коробке // Известия ВУЗов. Машиностроение. 2007. № 7. С. 32-36.
5. Darnell I., Hulbert G.M., Mousseau C.W. An Efficient Three-Dimensional Tire Model for Vehicle Dynamics Simulation // Mechanics of Structures and Machines. 1997. Vol. 25, iss. 1. P. 1-19. DOI: 10.1080/08905459708905277
6. Fukushima T., Shimonishi H. Simulation of a Vehicle Running onto a Curb by Using Tire and Vehicle FE models // Proc. of the 4th European LS-DYNA Users Conference, 2003. P. 1-7.
7. Фоминых А.Б., Комиссаров А.И. Модели взаимодействия колеса с единичными неровностями, предназначенные для определения динамической нагруженности трансмиссии колесной машины // Известия ВУЗов. Машиностроение. 2005. № 1. С. 29-37.
8. Davis D.S. A Radial-Spring Terrain-Enveloping Tire Model // Vehicle System Dynamics. 1974. Vol. 3. P. 55-69.
9. Лурье А.И. Аналитическая механика. М.: Физматгиз, 1961. 824 с.
10. Александров П.С. Лекции по аналитической геометрии. М.: Наука, 1968. 912 с.
Публикации с ключевыми словами: математическая модель, система подрессоривания, колесная машина, пространственное нагружение, системы координат, матрицы, дифференциальные уравнения, трансмиссия, несущая система
Публикации со словами: математическая модель, система подрессоривания, колесная машина, пространственное нагружение, системы координат, матрицы, дифференциальные уравнения, трансмиссия, несущая система
Смотри также:
- Оценка эффективности законов управления индивидуальным приводом движителей колесных транспортных комплексов
- Разработка закона распределения моментов по колесам многоосной колесной машины с электро-механической трансмиссией, выполненной по схеме «мотор-ось»
- Прогнозирование характеристик криволинейного движения многоосной колесной машины при различных законах всеколесного рулевого управления
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



