научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 12, декабрь 2013
DOI: 10.7463/1213.0645511
УДК 519.6
Россия, Уфа, Институт нефтехимии и катализа РАН
Россия, МГТУ им. Н.Э. Баумана
Введение
В настоящее время мировая промышленность ежегодно производит десятки тысяч тонн алюминийорганических соединений (АОС), большая часть которых используется в качестве сокатализаторов в полимеризационных процессах для получения полиэтилена, полипропилена, полиизопренового каучука и т.д. В Институте нефтехимии и катализа РАН (ИНК РАН, г. Уфа) ведутся исследования и разработка оригинальных двухкомпонентных нейтральных каталитических систем, состоящих из соединений металла переменной валентности (титана или циркония) и АОС, которые называются металлокомплексными катализаторами [1, 2]. Промышленное использование указанных катализаторов предполагает знание поведения реагирующей системы при изменении внешних условий (температуры, давления, концентрации реагентов и т.п.), что позволяет оптимизировать режим протекания реакции с целью обеспечения его безопасности и максимизации выхода продукта. Другими словами, для управления технологической установкой, в которой происходит каталитический синтез, требуется кинетическая модель химической реакции в присутствии металлокомплексных катализаторов. Такие же модели необходимы для повышения эффективности известных и конструирования новых катализаторов.
Проблема состоит в том, что химические реакции в присутствии металлокомплексных катализаторов представляют собой весьма сложные, быстро протекающие и далеко не полностью изученные процессы. Поставить и провести натурные химические эксперименты в широком интервале изменений условий проведения реакции – очень затратный, а иногда и опасный процесс. Поэтому необходимо, хотя бы качественно, прогнозировать поведение химической реакции во всех возможных условиях. С этой целью на основе результатов проведенных химических опытов необходимо, прежде всего, построить адекватную математическую модель реакции. Для сложных реакций металлокомплексного катализа эта модель включает в себя от 8 до 60 параметров, иногда отличающихся друг от друга на 20 и более порядков [3].
Работа посвящена задаче идентификации кинетических моделей химических реакций указанного класса, которая относится к классу обратных задач химической кинетики. Известно значительное число работ, посвященных этой задаче [4-6]. Большое число таких работ выполнено в ИНК РАН [7-10]. Как правило, в этих работах задача идентификации ставится как однокритериальная задача оптимизации невязки расчетных и экспериментальных данных. Недостаток такой постановки заключается в том, что в процессе идентификации игнорируется важная априорная информация об особенностях кинетики исследуемой химической реакции. Например, если имеются экспериментальные данные для нескольких температур, при которых проводилась реакция, то такая постановка не учитывает зависимость констант скоростей стадий от температуры по уравнению Аррениуса [11]. Если имеется априорная информация об индукционном периоде того или иного из веществ, участвующего в данной химической реакции [12], то однокритериальная постановка не позволяет принять в расчет эту информацию.
Особенность и новизна данной работы заключаются в постановке задачи идентификации как двухкритериальной, позволяющей учесть, как экспериментальные данные о кинетике исследуемой химической реакции, так и априорную информацию об этой реакции.
Постановка задачи многокритериальной оптимизации (МКО-задачи) фиксирует вектор варьируемых параметров задачи, множество допустимых значений этого вектора, вектор критериальных функций и, возможно, ограничения на значения компонентов этого вектора. Данная информация позволяет, как правило, выделить не одно решение задачи, но множество таких решений (множество Парето). Поэтому полагаем, как это часто делается в современных публикациях в данной области, что решением МКО-задачи является ее множество Парето. Множество Парето занимает в теории многокритериальной оптимизации исключительное место, поскольку, согласно известному принципу Эджворта-Парето, при «разумном» поведении лица, принимающего решения (ЛПР), выбор решения следует производить на множестве Парето [13].
Известно большое число методов Парето-аппроксимации, то есть методов построения некоторой конечномерной аппроксимации множества Парето. Обзор таких методов представлен, например, в работе [14]. В данной работе для решения задачи Парето-аппроксимации используем модифицированный метод адаптивных взвешенных сумм (Adaptive Weighted Sum, AWS) [15]. Базовый вариант метода предложили Рю, Ким и Ван (J-H. Ryu, S. Kim, H. Wan) в 2009 г. [16]. Метод основан на аддитивной свертке частных критериев оптимальности. В отличие от классического метода суммы взвешенных критериев (Weighted Sum, WS) [14], также использующего такую свертку, метод AWSпредполагает адаптацию весовых коэффициентов в процессе итераций на основе информации о текущем положении подобласти поиска. Одной из целей работы является апробация модифицированного метода AWSв процессе решения практических двухкритериальных обратных задах химической кинетики.
Для сокращения затрат на вычисление значений критериальных функций метод AWSиспользует метамодели этих функций. Рассматриваемые обратные задачи химической кинетики описываются системами обыкновенных дифференциальных уравнений, имеющими высокую жесткость. Отсюда вытекает высокая вычислительная сложность этих задач. Тот факт, что метод AWS использует метамодели критериальных функций, позволяет значительно сократить вычислительные затраты (без потери точности Парето-аппроксимации).
В первом разделе работы даем постановку двухкритериальных задач идентификации кинетики химических реакций гидроалюминирования олефинов алкилаланами HAlBui2 и ClAlBui2. Во втором разделе представляем использованное алгоритмическое и программное обеспечение. В третьем разделе приводим результаты вычислительных экспериментов и их обсуждение. В заключении формулируем основные результаты работы и очерчиваем перспективы ее развития.
1. Постановка двухкритериальных задач идентификация кинетических параметров реакции гидроалюминирования олефинов алкилаланами
1.1. Реакция гидроалюминирования олефинов алкилаланом HAlBu2
Математическая модель реакции представляет собой систему обыкновенных дифференциальных уравнений (ОДУ)
 (1)
(1)
Здесь и далее ![]() – концентрация реагирующего вещества
– концентрация реагирующего вещества ![]() , мол. доли;
, мол. доли; ![]() – константа скорости стадий реакции, 1/мин;
– константа скорости стадий реакции, 1/мин; ![]() – время, мин.;
– время, мин.; ![]() ;
; ![]() =[Cp2ZrH2·ClAlBu2]2 ‑ димер;
=[Cp2ZrH2·ClAlBu2]2 ‑ димер; ![]() =[Cp2ZrH2·ClAlBu2] ‑ мономер;
=[Cp2ZrH2·ClAlBu2] ‑ мономер; ![]() =HAlBu2;
=HAlBu2; ![]() =[Cp2ZrH2·HAlBu2·ClAlBu2] – тригидридный комплекс; Cp=C5H5.
=[Cp2ZrH2·HAlBu2·ClAlBu2] – тригидридный комплекс; Cp=C5H5.
Константы скорости подчиняются закону Аррениуса
 или
или  , (2)
, (2)
где ![]() и
и ![]() (энергия активации, ккал/моль) – константы, подлежащие оценке;
(энергия активации, ккал/моль) – константы, подлежащие оценке; ![]() – газовая постоянная, ккал/(моль*K);
– газовая постоянная, ккал/(моль*K); ![]() – температура, К.
– температура, К.
Экспериментальные данные представлены значениями концентраций реагирующих веществ при температурах -65 °С, -60 °С, -55 °С. Обозначим натурный эксперимент, проведенный при первой температуре T 65, при второй температуре – T 60, при третьей – T 55.
Введем набор констант реакции
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() ‑ наборы констант скоростей реакции для экспериментов T 65, T 60, T 55 соответственно.
‑ наборы констант скоростей реакции для экспериментов T 65, T 60, T 55 соответственно.
Во введенных обозначениях из уравнений (1) следует совокупность трех систем ОДУ
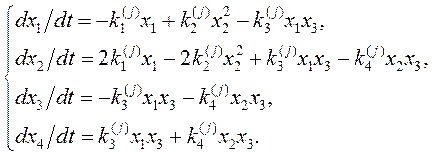
![]() . (3)
. (3)
Экспериментальные данные предоставлены в виде концентраций
 ,
, ![]() ,
, ![]() , (4)
, (4)
где ![]() – порядковый номер экспериментальной точки в
– порядковый номер экспериментальной точки в ![]() -ом эксперименте,
-ом эксперименте, ![]() – число наборов концентраций (4) для
– число наборов концентраций (4) для ![]() -ого эксперимента.
-ого эксперимента.
На константы реакций наложены ограничения
![]()
![]() , (5)
, (5)
![]() ,
, ![]() , (6)
, (6)
которые установлены квантово-химическими методами.
Рассматриваем два критерия оптимальности идентификации ‑ критерий MaXimum Squared Error (MXSE) и критерий Method of Least Squares Error (MLSE).
Критерий оптимальности MXSE имеет смысл максимума квадратов невязок концентраций и равен
 ,
, ![]() ,
, ![]() .
.
Здесь ![]() расчетное значение величины
расчетное значение величины ![]() .
.
Критерий MLSE отражает максимальную ошибку аппроксимации закона Аррениуса и представляет собой максимум невязок МНК-оценок констант уравнения Аррениуса:
 ,
, ![]() ,
, ![]() .
.
Здесь ![]() – отклонение расчетного значения
– отклонение расчетного значения ![]() константы от ее МНК-оценки
константы от ее МНК-оценки ![]() .
.
Двухкритериальная задача параметрической идентификации кинетической модели реакции ставится следующим образом: найти такие допустимые константы реакции ![]() ,
, ![]() , которые минимизируют критерии оптимальности MXSE
, которые минимизируют критерии оптимальности MXSE ![]() , MLSE
, MLSE ![]() .
.
1.2 Реакция гидроалюминирования олефинов алкилаланом ClAlBu2
Математическая модель реакции представляет собой систему ОДУ
| (8) |
где приняты следующие обозначения:
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Здесь X1= [Cp2ZrH2·ClAlBu2]2, X2= [Cp2ZrH2·ClAlBu2], X3= CH2CHR, X4= Cp2ZrCl(CH2CH2R), X5= HAlBu2, X6= Bu2Al(CH2CH2R), X7= Cp2ZrHCl, X8= [Cp2ZrH2·HAlBu2·ClAlBu2], X9= ClAlBu2, X10= [Cp2ZrHCl·ClAlBu2], X11= Cl2AlBu, X12= C4H8, X13= Сp2ZrCl2, X14= Cp2ZrClBu, X15= ClBuAl(CH2CH2R); R= C5H11, C6H13, C7H15, C8H17, Bu= C4H9, Cp= C5H5.
Экспериментальные данные предоставлены в виде, аналогичном (4):
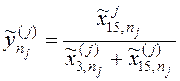 ,
, ![]() ,
, ![]() .
.
На константы реакций наложены ограничения
![]() ,
,
![]() .
.
В реакции гидроалюминирования олефинов кинетическая кривая расходования и накопления наблюдаемых веществ имеет s-образный вид: в начале процесса наблюдается медленное развитие реакции, которое сменяется периодом ускоренного развития реакции. Индукционным периодом вещества в химической реакции называют временной отрезок ![]() , в течение которого происходит медленное изменение концентрации этого вещества. При превышении верхнего предела отрезка
, в течение которого происходит медленное изменение концентрации этого вещества. При превышении верхнего предела отрезка ![]() происходит резкое увеличение или уменьшение скорости изменения концентрации вещества (рисунок 1).
происходит резкое увеличение или уменьшение скорости изменения концентрации вещества (рисунок 1).
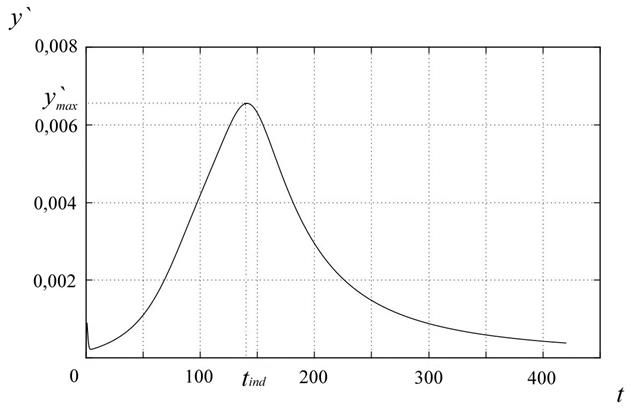
Рисунок 1 – К определению индукционного периода: ![]() ‑ скорость изменения концентрации рассматриваемого вещества
‑ скорость изменения концентрации рассматриваемого вещества
Как и в предыдущей задаче, рассматриваем два критерия оптимальности идентификации – критерий Sum Squared Error (SSE) и критерий Induction Time Squared Error (ITSE).
Критерий SSE имеет смысл суммы квадратов невязок концентраций:
 ,
, ![]() ,
, ![]() .
.
Критерий ITSE представляет собой квадрат невязки времени ![]() :
:
![]() .
.
Здесь ![]() и
и ![]() – расчетное и экспериментальное значения индукционного периода.
– расчетное и экспериментальное значения индукционного периода.
Таким образом, двухкритериальную задачу параметрической идентификации реакции гидроалюминирования олефинов алкилаланом ClAlBu2 (5) формулируем следующим образом: найти такие допустимые константы реакций ![]() ,
, ![]() , которые минимизируют критерии оптимальности SSE
, которые минимизируют критерии оптимальности SSE ![]() , ITSE
, ITSE ![]() .
.
2. Используемые алгоритмы и программное обеспечение
2.1. Постановка задачи многокритериальной оптимизации
Пусть множеством допустимых значений вектора варьируемых параметров Xявляется ограниченное и замкнутое множество ![]() . Положим, что критериальная вектор-функция
. Положим, что критериальная вектор-функция ![]() со значениями в критериальном пространстве
со значениями в критериальном пространстве ![]() определена в области
определена в области ![]() . ЛПР стремится минимизировать в этой области каждый из частных критериев оптимальности
. ЛПР стремится минимизировать в этой области каждый из частных критериев оптимальности ![]() , что условно записываем в виде
, что условно записываем в виде
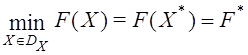 , (9)
, (9)
где векторы ![]() –искомое решение задачи многокритериальной оптимизации. Здесь и далее запись вида
–искомое решение задачи многокритериальной оптимизации. Здесь и далее запись вида ![]() , где
, где ![]() – вектор или некоторое счетное множество, означает размерность этого вектора или мощность множества соответственно.
– вектор или некоторое счетное множество, означает размерность этого вектора или мощность множества соответственно.
Вектор-функция ![]() выполняет отображение множества
выполняет отображение множества ![]() во множество
во множество ![]() , которое называется множеством достижимости. Множество и фронт Парето задачи (9) обозначаем
, которое называется множеством достижимости. Множество и фронт Парето задачи (9) обозначаем ![]() ,
, ![]() соответственно;
соответственно; ![]() ,
, ![]() . Конечномерные аппроксимации этих множеств обозначаем
. Конечномерные аппроксимации этих множеств обозначаем ![]() ,
, ![]() соответственно и называем архивными.
соответственно и называем архивными.
2.2. Метод адаптивных взвешенных сумм. Основными в методе AWS являются следующие процедуры.
Инициализация метода. Определяем значения свободных параметров метода: ![]() – начальный радиус области доверия (trust region radius);
– начальный радиус области доверия (trust region radius); ![]() – коэффициент сужения этой области;
– коэффициент сужения этой области; ![]() – минимальная величина радиуса. Случайным образом в области
– минимальная величина радиуса. Случайным образом в области ![]() выбираем центральную точку
выбираем центральную точку ![]() .
.
Определение центральной точки. На итерации ![]() центральную точку
центральную точку ![]() отыскиваем среди точек текущей Парето-аппроксимации
отыскиваем среди точек текущей Парето-аппроксимации ![]() , построенной на предыдущей итерации
, построенной на предыдущей итерации ![]() . С этой целью элементы текущих множеств
. С этой целью элементы текущих множеств ![]() сортируем по возрастанию первого частного критерия
сортируем по возрастанию первого частного критерия ![]() и представляем в виде линейных списков с прежними наименованиями. Расстояние
и представляем в виде линейных списков с прежними наименованиями. Расстояние ![]() архивной точки
архивной точки ![]() до ближайших к ней в списке
до ближайших к ней в списке ![]() точек определяет формула
точек определяет формула
![]() ,
, ![]() , (10)
, (10)
где ![]() – евклидова векторная норма. Алгоритм определения центральной точки
– евклидова векторная норма. Алгоритм определения центральной точки ![]() использует следующее правило.
использует следующее правило.
1) Если ![]() , то полагаем
, то полагаем ![]() , где
, где
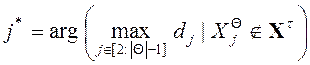 .
.
Здесь ![]()
![]() – множество точек, использованных в качестве центральных на всех предыдущих итерациях
– множество точек, использованных в качестве центральных на всех предыдущих итерациях ![]() . Иными словами, за центральную точку принимаем точку, во-первых, наиболее удаленную от других точек множества
. Иными словами, за центральную точку принимаем точку, во-первых, наиболее удаленную от других точек множества ![]() в смысле расстояния (10), и, во-вторых, не использованную на предшествующих итерациях.
в смысле расстояния (10), и, во-вторых, не использованную на предшествующих итерациях.
2) Если ![]() , то с равной вероятностью полагаем
, то с равной вероятностью полагаем ![]() или
или ![]() .
.
3) Если ![]() , то принимается
, то принимается ![]() .
.
Формирование метамоделей. Метамодель ![]() представляет собой квадратичную аппроксимацию функции
представляет собой квадратичную аппроксимацию функции ![]() в окрестности точки
в окрестности точки ![]() :
:
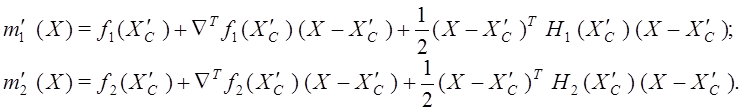
Здесь ![]() ,
, ![]() – вектор градиента и матрица Гессе функции
– вектор градиента и матрица Гессе функции ![]() в точке
в точке ![]() ;
; ![]() .
.
Если ![]() , то дополнительно строим метамодели
, то дополнительно строим метамодели
![]() ,
,
![]() ,
,
а если ![]() или
или ![]() – метамодель
– метамодель
![]() .
.
В ![]() весовые множители
весовые множители ![]() ,
, ![]() определяем по правилу
определяем по правилу
![]() ,
,
![]() ;
;
во ![]() – по правилу
– по правилу
![]() ;
;
в ![]() – по правилу
– по правилу ![]() . Константы
. Константы ![]() ,
, ![]() выбираются таким образом, чтобы обеспечить выполнение условий нормировки
выбираются таким образом, чтобы обеспечить выполнение условий нормировки ![]() .
.
В работе [16] задача формирования квадратичных метамоделей ![]() ,
, ![]() не раскрыта. Остановимся на этой задаче.
не раскрыта. Остановимся на этой задаче.
Для формирования квадратичных метамоделей ![]() ,
, ![]() используем центральный композиционный план (ЦКП) с центром в точке
используем центральный композиционный план (ЦКП) с центром в точке ![]() [17]. Для упрощения вычислений «звездное» плечо в ЦКП выбираем таким образом, чтобы этот план приобрел свойство ортогональности. В качестве ядра ЦКП используем полный факторный эксперимент. Легко видеть, что в общем случае необходимое число испытаний (вычислений значений критериальной функции) для построения одной метамодели равно
[17]. Для упрощения вычислений «звездное» плечо в ЦКП выбираем таким образом, чтобы этот план приобрел свойство ортогональности. В качестве ядра ЦКП используем полный факторный эксперимент. Легко видеть, что в общем случае необходимое число испытаний (вычислений значений критериальной функции) для построения одной метамодели равно
![]() ,
,
где ![]() – число испытаний в точках ядра плана,
– число испытаний в точках ядра плана, ![]() – число «звездных» точек,
– число «звездных» точек, ![]() – число испытаний в центре плана. Таким образом, в нашем случае (когда
– число испытаний в центре плана. Таким образом, в нашем случае (когда ![]() ) имеем
) имеем
![]() .
.
Серьезной проблемой при использовании ЦКП является генерация эффективной дробной реплики. Используем для этой цели функции Уолша [17].
Решение оптимизационных задач. Данная процедура предполагает решение задач оптимизации

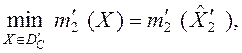 (11)
(11)
где текущую область доверия ![]() определяет формула
определяет формула
![]() .
.
Если ![]() , то решения
, то решения ![]() позволяют отыскать приближенно оптимальные по Парето точки
позволяют отыскать приближенно оптимальные по Парето точки ![]() , принадлежащие области доверия
, принадлежащие области доверия ![]() , путем решения оптимизационных задач
, путем решения оптимизационных задач

 . (12)
. (12)
Важно, что задачи (11), (12) представляют собой задачи оптимизации квадратичных функций, для решения которых известны высокоэффективные методы, алгоритмы и соответствующее программное обеспечение.
В процессе итераций текущий радиус области доверия уменьшаем по правилу ![]() до достижения минимально допустимой его величины
до достижения минимально допустимой его величины ![]() . Новое состояние архивного множества
. Новое состояние архивного множества ![]() получаем путем добавления в него точек
получаем путем добавления в него точек ![]() ,
, ![]() ,
, ![]() ,
, ![]() и исключения из полученного набора доминируемых решений. Аналогично, множество
и исключения из полученного набора доминируемых решений. Аналогично, множество ![]() формируем путем добавления в него точек
формируем путем добавления в него точек ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
2.3. Используемые модификации метода адаптивных взвешенных сумм
1) Повышение разнообразия множества архивных точек (модификация ![]() ). Наши исследования показали, что в некоторых случаях метод AWS обеспечивает аппроксимацию только части множества Парето, то есть не обеспечивает достаточное разнообразие множества архивных точек
). Наши исследования показали, что в некоторых случаях метод AWS обеспечивает аппроксимацию только части множества Парето, то есть не обеспечивает достаточное разнообразие множества архивных точек ![]() [18]. Суть модификации
[18]. Суть модификации ![]() [15] состоит в решении на каждой итерации в крайних точках архивного множества
[15] состоит в решении на каждой итерации в крайних точках архивного множества ![]() задач
задач
![]()
![]()
![]()
![]()
Здесь
![]()
![]()
2) Смещение области доверия (модификация ![]() ). Точки множества Парето могут в некоторых случаях плотно прилегать к одной из границ области определения. При решении таких задач метод AWS уменьшает радиус области доверия
). Точки множества Парето могут в некоторых случаях плотно прилегать к одной из границ области определения. При решении таких задач метод AWS уменьшает радиус области доверия ![]() на каждой итераций, сокращая в результате разнообразие архивных точек. Идея модификации
на каждой итераций, сокращая в результате разнообразие архивных точек. Идея модификации ![]() состоит в смещении центра области доверия «вглубь» области определения, не изменяя при этом ее радиуса [15].
состоит в смещении центра области доверия «вглубь» области определения, не изменяя при этом ее радиуса [15].
3) Нейросетевая аппроксимация целевых функций (модификация ![]() ). Идея данной модификации состоит в построении метамоделей критериальных функций с помощью искусственных нейронных сетей [15]. Поскольку на каждой итерации метода AWS аппроксимация критериальной функции производится в пределах «небольшой» области доверия
). Идея данной модификации состоит в построении метамоделей критериальных функций с помощью искусственных нейронных сетей [15]. Поскольку на каждой итерации метода AWS аппроксимация критериальной функции производится в пределах «небольшой» области доверия ![]() используем радиально-базисные нейронные сети [15].
используем радиально-базисные нейронные сети [15].
3. Результаты экспериментов
3.1. Реакция гидроалюминирования олефинов алкилаланом HAlBu2
Фронт Парето для задачи двухкритериальной параметрической идентификации реакции гидроалюминирования олефинов алкилаланом HAlBu2. (п. 1.1) получен с помощью модифицированного AWS-метода ![]() и представлен на рисунке 2. Из рисунка следует, что фронт является непрерывным и выпуклым. Метод
и представлен на рисунке 2. Из рисунка следует, что фронт является непрерывным и выпуклым. Метод ![]() обеспечил построение плотной и равномерной аппроксимации фронта Парето.
обеспечил построение плотной и равномерной аппроксимации фронта Парето.

Рисунок 2 – Фронт Парето для обратной задачи химической кинетики реакции гидроалюминирования олефинов алкилаланом HAlBu2 (выделено решение, выбранное ЛПР)
Выбор ЛПР компромиссного решения основан на физико-химическом смысле полученных результатов. На основании квантово-химических исследований данной реакции были сформулированы следующие выводы. Возможными каналами превращения вещества ![]() являются реакция димеризации и взаимодействие с очередной молекулой HAlBu2. В условиях избытка молекул HAlBu2 наиболее вероятно взаимодействие комплекса
являются реакция димеризации и взаимодействие с очередной молекулой HAlBu2. В условиях избытка молекул HAlBu2 наиболее вероятно взаимодействие комплекса ![]() с молекулой HAlBu2, что приводит к образованию экспериментально идентифицированного тригидридного комплекса
с молекулой HAlBu2, что приводит к образованию экспериментально идентифицированного тригидридного комплекса ![]() . Таким образом, энергия активация
. Таким образом, энергия активация ![]() должна быть меньше энергии активации
должна быть меньше энергии активации ![]() . Энергия активации обратной стадии (ей соответствует константа
. Энергия активации обратной стадии (ей соответствует константа ![]() ) должна быть больше энергии активации прямой стадии (константа
) должна быть больше энергии активации прямой стадии (константа ![]() ). Обратимая стадия каталитического процесса определяет общую скорость и эффективность реакции гидроалюминирования, то есть
). Обратимая стадия каталитического процесса определяет общую скорость и эффективность реакции гидроалюминирования, то есть ![]() ,
, ![]() ,
, ![]() . К тому же, константа скорости обратной стадии должна быть больше скорости прямой стадии. Перечисленным условиям удовлетворяет следующий набор констант:
. К тому же, константа скорости обратной стадии должна быть больше скорости прямой стадии. Перечисленным условиям удовлетворяет следующий набор констант:
 ;
; 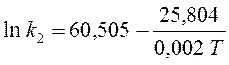 ;
;
 ;
;  ;
; ![]() .
.
На рисунке 2 выделено решение, соответствующее данному набору. Рисунок 3 иллюстрирует соответствие расчетных и экспериментальных данных. Зависимость констант скорости всех стадий от температуры подчиняется закону Аррениуса (рисунок 4). В интервале рассматриваемых температур полученные результаты удовлетворяют условиям (5), (6).
Рисунок 3 – Экспериментальные (![]() ) и расчетные (сплошная линия) концентрации вещества Х1: реакция гидроалюминирования олефинов алкилаланом HAlBui2
) и расчетные (сплошная линия) концентрации вещества Х1: реакция гидроалюминирования олефинов алкилаланом HAlBui2
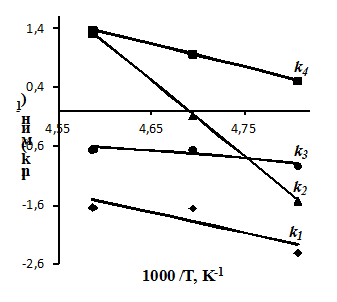
Рисунок 4 – Зависимости констант скоростей от температуры:
реакция гидроалюминирования олефинов алкилаланом HAlBui2; сплошная линия – закон Аррениуса; ![]() – расчетные точки
– расчетные точки
Результаты исследования показывают, что в реакции с алкилаланом HAlBui2 самой быстрой является стадия перехода комплекса ![]() в тригидридный комплекс
в тригидридный комплекс ![]() , то есть стадия
, то есть стадия ![]() (рисунок 5). Таким образом, на основании полученной кинетической модели рассматриваемой химической реакции подтверждено, что комплексы
(рисунок 5). Таким образом, на основании полученной кинетической модели рассматриваемой химической реакции подтверждено, что комплексы ![]() могут взаимодействовать с молекулой HAlBui2 с образованием тригидридного комплекса
могут взаимодействовать с молекулой HAlBui2 с образованием тригидридного комплекса ![]() , который ранее считался неактивным.
, который ранее считался неактивным.

Рисунок 5 – Скорости стадий реакции в функции температуры: ![]() – скорость i-ой стадии
– скорость i-ой стадии
3.2 Реакция гидроалюминирования олефинов алкилаланом ClAlBu2
Фронт Парето для задачи двухкритериальной идентификации реакции гидроалюминирования олефинов алкилаланом ClAlBu2 представлен на рисунке 6. Из рисунка следует, что этот фронт является почти вертикальным, то есть что имеет место слабая зависимость критерия SSEот варьируемых параметров (в рассматриваемых диапазонах их изменения). Задачи с таким фронтом представляют значительную сложность для классического метода WS [15]. Использованный нами метод ![]() обеспечил построение плотной и равномерной аппроксимации фронта Парето.
обеспечил построение плотной и равномерной аппроксимации фронта Парето.
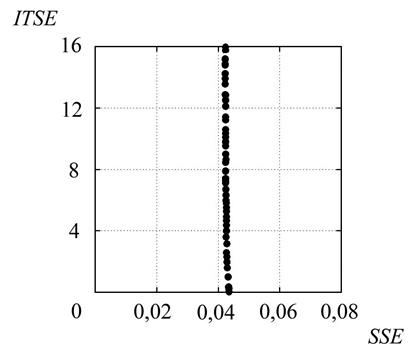
Рисунок 6 – Фронт Парето для обратной задачи гидроалюминирования олефинов алкилаланом ClAlBu2
Для всех указанных на рисунке точек фронта Парето полученные наборы констант лежат в пределах допустимых значений и одинаково хорошо описывают экспериментальные данные. Для ЛПР все эти наборы равноценны, так что, с формальной точки зрения, задача является однокритериальной. С другой стороны, в реакции гидроалюминирования олефинов алкилаланом ClAlBu2 из всех 15 реагирующих веществ наблюдаются лишь вещества ![]() ,
, ![]() , точнее говоря, известны лишь концентрации этих веществ в некоторые моменты времени. Эти экспериментальные данные одинаково хорошо описывают целые области пространства кинетических параметров. За счет использования априорной информации об индукционном периоде образования продукта реакции удалось сузить эти области. Другими словами, двухкритериальная постановка задачи позволила отбросить заведомо некорректные решения.
, точнее говоря, известны лишь концентрации этих веществ в некоторые моменты времени. Эти экспериментальные данные одинаково хорошо описывают целые области пространства кинетических параметров. За счет использования априорной информации об индукционном периоде образования продукта реакции удалось сузить эти области. Другими словами, двухкритериальная постановка задачи позволила отбросить заведомо некорректные решения.
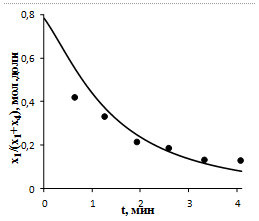
Согласие расчетных и экспериментальных данных для рассматриваемой задачи иллюстрирует рисунок 7. Отклонение расчетных данных от экспериментальных в начале реакции объясняется погрешностью экспериментальных данных. Согласно расчетным данным, время индукционного периода реакции составляет около 90 минут, что удовлетворительно совпадает с экспериментальными данными.

Рисунок 7 – Экспериментальные (![]() ) и расчетные (сплошная линия) концентрации вещества
) и расчетные (сплошная линия) концентрации вещества ![]() : реакция гидроалюминирования олефинов алкилаланом ClAlBui2
: реакция гидроалюминирования олефинов алкилаланом ClAlBui2
Заключение
Предшествующие работы, выполненные в ИНК РАН, позволяют сделать следующие выводы.
В случае, когда натурные эксперименты проводятся при различных температурах, последовательное решение обратных задач для каждой температуры и последующее применение метода наименьших квадратов для оценки энергии активации не всегда дают удовлетворительные результаты. Так, для некоторых стадий энергия активации может принимать отрицательные значения, для некоторых стадий константы скорости не подчиняются уравнению Аррениуса.
В некоторых работах для оценки кинетических параметров используют постановку задачи, в которой определяются не константы скоростей стадий реакции, а энергия активации ![]() и предэкспоненциальный множитель
и предэкспоненциальный множитель ![]() , которые связаны между собой линейной зависимостью по уравнению Аррениуса. Однако в реальных условиях используемые значения температур являются осредненными по объему реагирующих веществ. Потому при таком подходе расчетные данные могут описывать эксперимент с большой погрешностью.
, которые связаны между собой линейной зависимостью по уравнению Аррениуса. Однако в реальных условиях используемые значения температур являются осредненными по объему реагирующих веществ. Потому при таком подходе расчетные данные могут описывать эксперимент с большой погрешностью.
Альтернативный подход к решению задачи обратной кинетики, основанный на двухкритериальной постановке, предложен в данной работе. Двухкритериальная оценка кинетических параметров химической реакции позволяет приять в расчет структурные связи между экспериментами путем учета зависимости констант скоростей стадий реакции от температуры по уравнению Аррениуса.
Данный подход применен в работе, во-первых, к задаче идентификации кинетической модели реакции гидроалюминирования олефинов алкилаланом HAlBu2. Полученные результаты в достаточной степени соответствуют результатам кинетического эксперимента (относительная ошибка отклонения расчетных и экспериментальных данных находится в пределах 10 %). Предложенная на основе этих результатов кинетическая модель реакции позволяет предсказать состав реакционной массы при различных температурах и начальных соотношениях реагентов.
Во-вторых, предложенный подход применен к задаче идентификации кинетической модели реакции гидроалюминирования олефинов алкилаланом ClAlBu2. В данном случае этот подход позволил сузить множество решений задачи за счет использования априорной информации об индукционном периоде образования продукта реакции. Двухкритериальная постановка задачи позволила отбросить заведомо некорректные решения и получить хорошее соответствие расчетных и экспериментальных данных. Длительности индукционного периода и быстрого роста концентрации наблюдаемого вещества хорошо согласуются с экспериментальными данными, что свидетельствует о правильном выборе механизма реакции и об адекватности построенной кинетической модели.
Авторы планируют применение рассмотренного многокритериального подхода к идентификации кинетических моделей других реакций металлокомплексного катализа. Также планируется использование этого подхода для определения оптимальных, согласованных между собой значений управляющих параметров кинетической модели, путем варьирования концентрации исходных реагентов, температур, давлений и объёмов реагирующих веществ, а также состава и количества катализаторов, которые обеспечивают максимальный выход полезных конечных продуктов.
Работа поддержана грантом РФФИ №12-07-00324-а «Структурная и параметрическая идентификация кинетических моделей реакций нейтрального металлокомплексного катализа» и грантом №12-07-31029 «Идентификация механизма реакции гидроалюминирования олефинов параллельными методами».
Список литературы
1. Parfenova L.V., Vil’danova R. F., Pechatkina S. V., Khalilov L.M., Dzhemilev U.M. Zr,Al-complexes as new reagents for olefin hydrometallation // J. Organomet. Chem. 2007. Vol. 692. Р. 3424-3429.
2. Pankratyev E.Y., Tyumkina T.V., Parfenova L.V., Khalilov L.M., Khursan S.L., Dzhemilev U.M. DFT study on mechanism of olefin hydroalumination by XAlBui2 in the presence of Cp2ZrCl2 catalyst. I. Simulation of intermediate formation in reaction of HAlBui2 with Cp2ZrCl2 // Organometallics. 2009. Vol. 28, no. 4. P. 968-977.
3. Григорьева Н.Г., Джемилев У.М., Кутепов Б.И., Балаев А.В., Губайдуллин И.М., Хазипова А.Н., Галяутдинова Р.Р. Разработка кинетической модели димеризации α-метилстирола на цеолите типа Y // Химическая промышленность. 2004. № 9. С. 31-36.
4. Быков В.И., Журавлев В.М. Моделирование и оптимизация химико-технологических процессов: учеб. пособие. М.: РХТУ им. Д.И. Менделеева, 2011. 308 с.
5. Ермакова А., Гудков А.В., Аникеев В.И. Идентификация кинетических моделей // Кинетика и катализ. 1997. Т. 38, № 2. С. 309-318.
6. Темкин О.Н. О кинетических моделях многомаршрутных реакций в гомогенном металлокомплексном катализе // Кинетика и катализ. 2012. Т. 53, № 3. С. 326-357.
7. Балаев А.В., Парфенова Л.В., Губайдуллин И.М., Русаков С.В., Спивак С.И., Халилов Л.М., Джемилев У.М. Механизм реакции циклоалюминирования алкенов триэтилалюминием в алюмациклопентаны, катализируемой Cp2ZrCl2 // Доклады АН. 2001. Т. 381, № 3. С. 364-367.
8. Parfenova L.V., Balaev A.V., Gubaidullin I.M., Abzalilova L.R., Pechatkina S.V., Khalilov L.M., Spivak S.I., Dzhemilev U.M. Kinetic Model of Olefins Hydrometallation by HAlBui2 and Al Bui3 in the Presence Cp2ZrCl2 Catalyst // Int. J. Chem. Kinet. 2007. Vol. 39, no. 6. Р. 333-339.
9. Губайдуллин И.М., Рябов В.В., Тихонова М.В. Применение индексного метода глобальной оптимизации при решении обратных задач химической кинетики // Вычислительные методы и программирование. Новые вычислительные технологии. 2011. Т. 12. С. 137-145. Режим доступа: http://num-meth.srcc.msu.ru/ (дата обращения 01.12.2013).
10. Ахметов И.В., Бобренёва Ю.О., Губайдуллин И.М., Новичкова А.В. Математическое моделирование сложных химических реакций в присутствии металлокомплексных катализаторов на основе многоядерных вычислительных систем // Системы управления и информационные технологии. 2013. № 2.1 (52) . С. 111-115.
11. Штиллер В. Уравнение Аррениуса и неравновесная кинетика: пер. с англ. М.: Мир, 2000. 176 с.
12. Хилько А.В., Спивак С.И., Губайдуллин И.М., Парфенова Л.В. О математическом моделировании индукционного периода химических реакций // Системы управления и информационные технологии. 2008. № 1.2 (31). С. 264-267.
13. Ларичев О.И. Теория и методы принятия решений: учебник для ВУЗов. М.: Университетская книга, Логос, 2006. 392 с.
14. Карпенко А.П., Митина Е.В., Семенихин А.С. Популяционные методы аппроксимации множества Парето в задаче многокритериальной оптимизации. Обзор // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012. № 4. Режим доступа: http://www.technomag.edu.ru/doc/363023.html (дата обращения 16.12.2013).
15. Карпенко А.П., Савелов А.С. Модифицированный метод адаптивных взвешенных сумм в задаче многокритериальной оптимизации //Наука и образование. МГТУим. Н.Э. Баумана. Электрон. журн. 2013. № 11. DOI: 10.7463/1113.0632468
16. Ryu J.-H., Kim S., Wan H. Pareto front approximation with adaptive weighted sum method in multiobjective simulation optimization // Proc. of the 2009 Winter Simulation Conference (WSC), 13-16 December 2009, Austin. 2009. P. 623-633. Available at: http://www.informs-sim.org/wsc09papers/060.pdf , accessed 01.11.2013.
17. Асатурян В.И. Теория планирования эксперимента. М.: Радио и связь, 1983. 248 с.
18. Карпенко А.П., Савелов А.С., Семенихин А.С. Адаптивный метод взвешенных сумм в задаче Парето-аппроксимации // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012. № 6. Режим доступа: http://www.technomag.edu.ru/doc/423283.html (дата обращения 16.12.2013).
Публикации с ключевыми словами: многокритериальная оптимизация, множество Парето, параметрическая идентификация, метод адаптивных взвешенных сумм, обратная задача химической кинетики, двухкомпонентная нейтральная каталитическая система, металл переменной валентности, алюминийорганическое соединение, гидроалюминирование олефинов алкилаланами
Публикации со словами: многокритериальная оптимизация, множество Парето, параметрическая идентификация, метод адаптивных взвешенных сумм, обратная задача химической кинетики, двухкомпонентная нейтральная каталитическая система, металл переменной валентности, алюминийорганическое соединение, гидроалюминирование олефинов алкилаланами
Смотри также:
- Модифицированный метод адаптивных взвешенных сумм в задаче многокритериальной оптимизации
- Гибридизация методов зондирования области поиска и адаптивных взвешенных сумм в задаче Парето-аппроксимации
- 77-30569/363023 Популяционные методы аппроксимации множества Парето в задаче многокритериальной оптимизации. Обзор.
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||