научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#3 март 2007
УДК 528.854
А.В. Бобков, Ле Хай Ха
Московский государственный
технический
университет имени Н.Э.Баумана
Введение
Задача сопоставления изображений сводится к определению наиболее вероятного положения имеющегося образца T(x,y) на изображении I(x,y), то есть к отысканию преобразованию координат f(x,y) и преобразования яркости g(I), обеспечивающих максимум некоторого функционала качества совпадения J(f,g):
![]() (1)
(1)
Выбор преобразования координат f(x,y) определяется как числом степеней свободы системы камера-объект, так и доступной информацией о числе степеней свободы объекта. В самом простом случае требуется определить смещение одного изображения относительно другого, то есть преобразование координат является преобразованием параллельного переноса:
![]()
Если камера и объект могут располагаться под различным углом либо на различном расстоянии друг от друга, то преобразование становится преобразованием подобия с четырьмя параметрами – смещение по двум осям (Dx,Dy), поворот j и масштаб M:
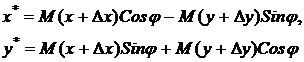
В более сложных случаях, когда линия визирования не ортогональна сцене, необходимо использовать проективное преобразование, имеющее девять параметров:
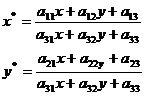
В более сложных случаях, например, когда сцену недопустимо считать плоской или необходимо учитывать трехмерность ее объектов, приходится использовать локальные преобразования, отдельно для каждого фрагмента сцены.
Выбор параметров преобразования яркости выполняется только при использовании яркостей точек изображения, поскольку методы, использующие ключевые точки, как правило, позволяют добиться инвариантности к преобразованию яркости. Наиболее распространенный метод заключается в линейной коррекции яркости по двум параметрам – яркости и контрастности наблюдаемого изображения, которые являются, по сути, математическим ожиданием и дисперсией яркости в кадре или последовательности кадров.
Увеличение количества параметров преобразования и рост сложности пространственного преобразования f(x,y) ведут к быстрому росту количества вычислений. Поэтому во многих практических задачах используется упрощенная модель преобразования, использующая небольшое количество параметров. Остальные параметры либо считаются постоянными, либо их значения оцениваются из других источников.
Неучтенные геометрические искажения
К неучтенным геометрическим искажениям относятся все пространственные преобразования, которые не учитываются в процессе сопоставления. Они могут возникать из-за неопределенностей процесса наблюдения или из-за неточности модели наблюдения.
К первой группе относятся неучтенные нелинейности оптической системы, отклонение линии визирования от нормали к плоскости наблюдения и т.д. Ко второй группе относится выпадение части параметров из процесса поиска из-за предположения об их неизменности, ошибки дискретизации параметров и другие.
Большинство этих ошибок нормально распределено вблизи конструктивно определенных параметров.
Рассмотрим ситуацию, когда в число параметров поиска входит только параметры сдвига, поворота и масштабирования (x,y,j,M), причем они ищутся с шагами квантования Dx, Dy, Dj и DM соответственно. Будем считать, что поворот изображения осуществляется вокруг его центра. Рассмотрим возникающие ошибки квантования.
Из-за квантования по сдвигу с шагом Dx=Dy максимум функции поиска размоется на величину ex=Dx. Поскольку обычно Dx=1, то величина e пренебрежимо мала.
Из-за квантования по углу поворота Dj отклики в пространстве поиска сместятся относительно своего реального положения на величину ej:
![]() ,
,
где N – размер изображения. Поскольку Dj относительно мало, то можно считать, что ej линейно зависит от Dj:
![]() .
.
Из-за квантования по масштабу DM отклики в пространстве поиска сместятся относительно своего реального положения на величину eМ:
![]() .
.
Так, при Dj =10о, DM=10% и размерах образца 256х256 (N=256) имеем:
ej=11 пикселей, eМ=12,8 пикселей.
|
|
|
|
|
а) |
б) |
в) |
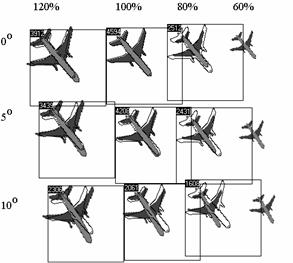
Рисунок 1. Поиск объекта при наличии неучтенных геометрических искажений
а) образец
б) исходное изображение с найденными объектами
в) отклики объектов в пространстве поиска
Коррекция искажениий в пространстве поиска
Таким образом,
воздействие неучтенных искажений приводит к искажению формы функции совпадения J(x): ее главный максимум размывается пропорционально
величине ошибки. Если определению подлежат n параметров, то воздействие ошибки e приведет к размытию функции совпадения на xi±e, в результате чего главный максимум уменьшится в ![]() раз, то есть
довольно существенно. Таким образом, начиная с некоторых значений e,
главный максимум уменьшится настолько, что затеряется среди ложных локальных
максимумов, и его отыскание станет невозможным. Кроме того, характер размытия
не является равномерным (рис.1в) и зависит от формы образца. Распределение
ошибки определения положения объекта также будет иметь сложную форму, например
– кольцеобразную, с провалом на месте реального положения объекта (рис.2a).
раз, то есть
довольно существенно. Таким образом, начиная с некоторых значений e,
главный максимум уменьшится настолько, что затеряется среди ложных локальных
максимумов, и его отыскание станет невозможным. Кроме того, характер размытия
не является равномерным (рис.1в) и зависит от формы образца. Распределение
ошибки определения положения объекта также будет иметь сложную форму, например
– кольцеобразную, с провалом на месте реального положения объекта (рис.2a).
Чтобы внести необходимую нечувствительность к нескомпенсированным искажениям (т.е. робастность), необходимо предусмотреть восстановление положения главного максимума функции совпадения. Один из возможных методов заключается в поиске наиболее массивной области функции совпадения. Он реализуется следующим образом.
Пусть величина размытия известна и равна e. Разобъем пространство поиска на гиперкубы с ребром в 2e, найдем сумму значений функции совпадений в каждом гиперкубе. Очевидно, что самый «массивный» гиперкуб Г лежит вблизи главного максимума и содержит его.
Найдем центр масс гиперкуба Г :
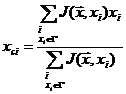 (2)
(2)
Построим новый гиперкуб Г1 с центром хс и ребром 2e, и по формуле (2) также найдем его центр масс хс1.Центр масс хс1 можно считать оценкой искомого положения главного максимума.
Можно продолжать итеративное уточнение положения центра масс по формуле (2), однако эксперименты показали, что этого не требуется. Две первые итерации дают достаточно точные результаты, и существенного роста точности с увеличением количества итераций не происходит.
Экспериментальная проверка эффективности коррекции неучтенных воздействий
Рассмотрим, как зависит качество поиска объекта от выбранного размера области в пространстве поиска и от количества проходов с использованием (2).
Поскольку форма главного максимума функции совпедения зависит не только от геометрических искажений, но и от типа объекта, необходимо набирать статистику на разных по характеру изображениях. Целесообразно поступить следующим образом. Возьмем исходное изображение, например, аэрофотоснимок местности со средним количеством объектов. В качестве второго изображения возьмем тот же снимок, но с геометрическими искажениями заданного вида. Разобъем исходное изображение на большое количество кадров, и будем искать их положение на втором изображении. Таким образом, получится два ряда значений положения: одно – вычисленное процедурой сопоставления, и второе – реальное положение, вычисленное из априорных данных. Теперь не составляет труда набрать требуемый объем статистических данных об ошибке при различных параметрах процедуры распознавания. Ошибкой будем считать отклонение вычисленного положения от реального на величину больше e.
Количество экспериментов примем равным 20 000. Результаты экспериментов сведем в таблицу 1.
Из таблицы видно, что использование коррекции позволяет существенно увеличить точность сопоставления изображений. Точность также зависит и от размера гиперкуба, в котором происходит восстановление максимума. Размер гиперкуба должен увеличиваться на каждой итерации. Для поставленных условий эксперимента оптимальный размер гиперкуба составляет 8 для первой итерации и 16 для последующих. Дополнительные исследования показали, что такое соотношение размеров будет близко к оптимальному для широкого круга задач.
Таблица 1. Зависимость ошибки от размера гиперкуба в алгоритме коррекции геометрических искажений
|
Размер окрестности |
Количество ошибок, % |
|||||
|
1й проход |
2й проход |
при e=10 |
при e=20 |
при e=40 |
||
|
Искажение – поворот изображения на 5о |
||||||
|
Без коррекции |
43% |
37% |
29% |
|||
|
4х4 |
4х4 |
19% |
14% |
8% |
||
|
4х4 |
8х8 |
7% |
4% |
3% |
||
|
8х8 |
8х8 |
11% |
5% |
3% |
||
|
8х8 |
16х16 |
5% |
3% |
2% |
||
|
16х16 |
16х16 |
9% |
3% |
2% |
||
|
16х16 |
16х32 |
25% |
8% |
6% |
||
|
8х8 |
16х16 |
16х16 |
4% |
3% |
2% |
|
|
Искажение – увеличение изображения на 10% |
||||||
|
Без коррекции |
41% |
28% |
27% |
|||
|
16х16 |
16х16 |
17% |
3% |
3% |
||
|
|
|
|
|
|
|
|
Из таблицы также видно, что увеличение количества итераций не приводит к существенному росту точности, и двух-трех итераций поиска оказывается достаточно.
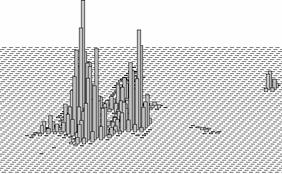
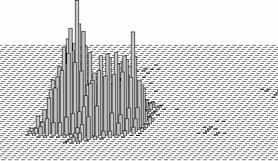
На рисунке 2 показано распределение ошибки при использовании коррекции и без него. Видно, что при отсутствии коррекции ошибка распределена в виде кольцеобразной структуры. При использовании коррекции элементы кольца мигрируют к общему центру масс и образуют гауссоиду.
|
а) |
б) |
Рисунок 2. Распределение ошибок при сопоставлении изображений (по выборке из 20 000 измерений) в условиях неучтенных геометрических искажений
а) Сопоставление с использованием максимума функции совпадения
б) Сопоставление с использованием восстановленного максимума по центру масс гиперкуба. Количество ошибок уменьшилось с 26% до 4%.
Выводы
Небольшие геометрические искажения объектов в задаче сопоставления объектов могут быть успешно скорректировани при использовании описанного алгоритма. Приведенные исследования показали высокую эффективность алгоритма, и наметили подходы к выбору оптимальных параметров коррекции. Использование объектов с допустимыми геометрическими искажениями позволяет существенно снизить количество излишних параметров, подлежащих определению, и тем самым уменьшить обший объем вычислений. Такое увеличение производительности без существенной потери точности и надежности имеет ключевое значение для всех приложений, ориентированных на работу в режиме реального времени.
Публикации с ключевыми словами: распозначание объектов, компенсация искажений
Публикации со словами: распозначание объектов, компенсация искажений
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||