научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#2 февраль 2007
А.Г. Афанасенко
Научно-технологический центр,
ОАО «Сода»,
г. Стерлитамак
Процесс карбонизации обусловлен следующими характеристиками:
- не все цели управления могут быть выражены в количественных соотношениях (например, размер, форма и однородность кристаллов гидрокарбонатов натрия);
- между рядом параметров, оказывающих влияние на процесс карбонизации нельзя установить точные количественные зависимости (например, зависимость между степенью утилизации натрия и концентрацией исходных веществ в аммонизированном рассоле) [1];
- невозможно с заданной точностью за заданное время провести анализ и прогноз изменения модели технологического процесса [2], описывающей кинетику физико-химических превращений.
Несмотря на то, что карбонизационная колонна является сложным нестационарным объектом, опытный оператор удовлетворительно справляется с задачей управления не только одной карбонизационной колонной, но и всем отделением карбонизации, формулируя управляющее воздействие в виде нечётких высказываний, например: «уменьшить отбор суспензии», «немного увеличить расход воды на охлаждение» и т.д.
Исходя из вышесказанного, мы предлагаем разработать математическую модель карбонизационной колонны на основе нечёткой логики (логико-лингвистическую модель).
В логико-лингвистических моделях для управления сложными объектами используется информация, представленная в лингвистической форме, и отражает качественные свойства объекта. Такая модель основывается на знаниях об объекте, полученных от компетентного в предметной области человека, – эксперта, который на основе своего опыта способен формулировать и эффективно решать поставленные задачи.
Для качественной оценки режимов работы карбонизационной колонны нужно определить понятие номинального режима. Это режим, при котором обеспечивается высокая степень использования натрия, хорошее качество осаждённого бикарбоната натрия, высокая степень использования двуокиси углерода и аммиака и производительность колонны не ниже заданной [1]..
Нормальный режим работы карбонизационной колонны обеспечивается стабилизацией ряда переменных состояния. При этом эти переменные близкие к номинальным значениям, определяемым из условий регламентного функционирования колонны. Параметрами состояния являются: температура суспензии, температура верхней части колонны (зона завязки кристаллов), температура отходящих газов, концентрация двуокиси углерода в отходящем газе колонны, прямой титр суспензии, уровень жидкости в колонне. Количество этих переменных может быть и больше.
При существенном отклонении значений параметров от номинальных, оператор добивается стабильного состояния процесса карбонизации. Обеспечив стабильное состояние, оператор на основании показаний приборов и результатах химического анализа решает, оставить имеющиеся технологические параметры в качестве номинальных или выбрать новые.
Предлагается разработать логико-лингвистическую модель карбонизационной колонны в четыре этапа, а именно:
1 этап. На данном этапе выбрать минимально необходимое число входных и выходных параметров карбонизационной колонны, дающих достаточное количество информации об объекте. Будем считать, что дрейф параметров состояния объекта отсутствует. В дальнейшем необходимо будет ввести в качестве параметра состояния величину, характеризующую степень зарастания внутренних поверхностей колонны осаждённым гидрокарбонатом натрия.
2 этап. Разделить параметры на нечёткие регионы [4]. Нечёткие параметры формализуются через значения функций принадлежности μ(x), принимающих любые промежуточные значения от 0 до 1, в лингвистические понятия «высокая», «низкая», «нормальная». Данная совокупность лингвистических понятий образует терм, т.е. множество значений переменных [3, 4]. На основании экспертных оценок для каждого нечёткого параметра определено количество, форма и взаимное расположение функций принадлежности. Функции принадлежности представлены на рис.. 1–5.

Рис. 1.. Функции принадлежности для входных параметров: текущая температура суспензии и предыдущая температура суспензии

Рис. 2. Функции принадлежности для входного параметра: температура охлаждающей воды
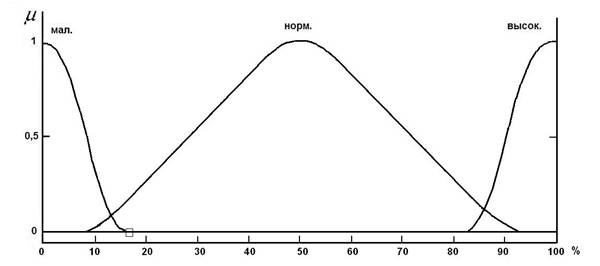
Рис. 3. Функции принадлежности для выходного параметра: расход охлаждающей воды

Рис. 4. Функции принадлежности для выходного параметра: расход газа первого входа

Рис. 5. Функции принадлежности для выходного параметра: расход газа второго входа
3 этап. Основой нечёткой логико-лингвистической модели служит таблица качественного описания процесса карбонизации (база нечётких правил) при различных нарушениях технологического режима, составленная по литературным источникам [1] и на основе опроса операторов-технологов.
Сформированные правила проверялись на полноту/избыточность и непротиворечивость. Данный этап является наиболее ответственным при разработке логико-лингвистической модели. Фрагмент базы нечетких правил представлен ниже:
…..
1 Если (Т1сусп = ОЧЕНЬ ВЫСОКАЯ) и (Т2сусп = ОЧЕНЬ ВЫСОКАЯ) и (Тводы= НОРМАЛЬНАЯ) тогда (Fводы= БОЛЬШОЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
2 Если (Т1сусп = ОЧЕНЬ ВЫСОКАЯ) и (Т2сусп = ОЧЕНЬ ВЫСОКАЯ) и (Тводы= ВЫСОКАЯ) тогда (Fводы= БОЛЬШОЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
3 Если (Т1сусп = ОЧЕНЬ ВЫСОКАЯ) и (Т2сусп = ВЫСОКАЯ) и (Тводы= НОРМАЛЬНАЯ) тогда (Fводы= БОЛЬШОЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
4 Если (Т1сусп = ВЫСОКАЯ) и (Т2сусп = ОЧЕНЬ ВЫСОКАЯ) и (Тводы= НОРМАЛЬНАЯ) тогда (Fводы= БОЛЬШОЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
5 Если (Т1сусп = ОЧЕНЬ НИЗКАЯ) и (Т2сусп = ОЧЕНЬ НИЗКАЯ) и (Тводы= ВЫСОКАЯ) тогда (Fводы = МАЛЫЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
6 Если (Т1сусп = ОЧЕНЬ ВЫСОКАЯ) и (Т2сусп = НОРМАЛЬНАЯ) и (Тводы= НИЗКАЯ) тогда (Fводы = НОРМАЛЬНЫЙ) (Fгаза1= НИЗКАЯ) (Fгаза2= НИЗКАЯ)
7 Если (Т1сусп = ОЧЕНЬ ВЫСОКАЯ) и (Т2сусп = ВЫСОКАЯ) и (Тводы= ВЫСОКАЯ) тогда (Fводы= БОЛЬШОЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
8 Если (Т1сусп = ОЧЕНЬ ВЫСОКАЯ) и (Т2сусп = НОРМАЛЬНАЯ) и (Тводы= НОРМАЛЬНАЯ) тогда (Fводы= БОЛЬШОЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
9 Если (Т1сусп = ОЧЕНЬ ВЫСОКАЯ) и (Т2сусп = НОРМАЛЬНАЯ) и (Тводы= ВЫСОКАЯ) тогда (Fводы= БОЛЬШОЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
10 Если (Т1сусп = ВЫСОКАЯ) и (Т2сусп = ВЫСОКАЯ) и (Тводы= НОРМАЛЬНАЯ) тогда (Fводы= БОЛЬШОЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
11 Если (Т1сусп = ВЫСОКАЯ) и (Т2сусп = ВЫСОКАЯ) и (Тводы= ВЫСОКАЯ) тогда (Fводы= БОЛЬШОЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
12 Если (Т1сусп = ВЫСОКАЯ) и (Т2сусп = ОЧЕНЬ ВЫСОКАЯ) и (Тводы= НИЗКАЯ) тогда (Fводы= НОРМАЛЬНЫЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
13 Если (Т1сусп = НИЗКАЯ) и (Т2сусп = ОЧЕНЬ ВЫСОКАЯ) и (Тводы= НОРМАЛЬНАЯ) тогда (Fводы= МАЛЫЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
14 Если (Т1сусп = НИЗКАЯ) и (Т2сусп = ОЧЕНЬ ВЫСОКАЯ) и (Тводы= ВЫСОКАЯ) тогда (Fводы= МАЛЫЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
15 Если (Т1сусп = НИЗКАЯ) и (Т2сусп = ВЫСОКАЯ) и (Тводы= НОРМАЛЬНАЯ) тогда (Fводы= МАЛЫЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
16 Если (Т1сусп = НИЗКАЯ) и (Т2сусп = ВЫСОКАЯ) и (Тводы= ВЫСОКАЯ) тогда (Fводы= МАЛЫЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
17 Если (Т1сусп = НИЗКАЯ) и (Т2сусп = НОРМАЛЬНАЯ) и (Тводы= НОРМАЛЬНАЯ) тогда (Fводы= МАЛЫЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
18 Если (Т1сусп = НИЗКАЯ) и (Т2сусп = НОРМАЛЬНАЯ) и (Тводы= ВЫСОКАЯ) тогда (Fводы= МАЛЫЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
19 Если (Т1сусп = НОРМАЛЬНАЯ) и (Т2сусп = НОРМАЛЬНАЯ) и (Тводы= ВЫСОКАЯ) тогда (Fводы= НОРМАЛЬНЫЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
20 Если (Т1сусп = НОРМАЛЬНАЯ) и (Т2сусп = НОРМАЛЬНАЯ) и (Тводы= НИЗКАЯ) тогда (Fводы= НОРМАЛЬНЫЙ) (Fгаза1= НОРМАЛЬНЫЙ) (Fгаза2= НОРМАЛЬНЫЙ)
…..
где: Т1сусп – текущая температура суспензии; Т2сусп – предыдущая температура суспензии; Тводы – температура охлаждающей воды; Fгаза1 – расход газа первого входа; Fгаза2 – расход газа второго входа; Fводы – расход охлаждающей воды.
4 этап. Следующим этапом является поиск такой последовательности воздействий, которые переводили бы объект из имеющегося состояния в состояние близкое к оптимальному, для каждой конкретной технологической ситуации. В качестве критерия можно использовать традиционные показатели качества (степень использования натрия, степень карбонизации, степень использования двуокиси углерода).
С помощью программной системы MatLab (пакет Fuzzy Logic Toolbox) проводим имитационное моделирование исследуемого процесса. В системе MatLab программируются все функции принадлежности и база нечётких правил [5]. Пример графического изображения поверхности отклика (пространство управления регулятора [6]) приведен на рис.. 6 и 7..

Рис. 6 – Поверхность отклика переменной: расход охлаждающей воды
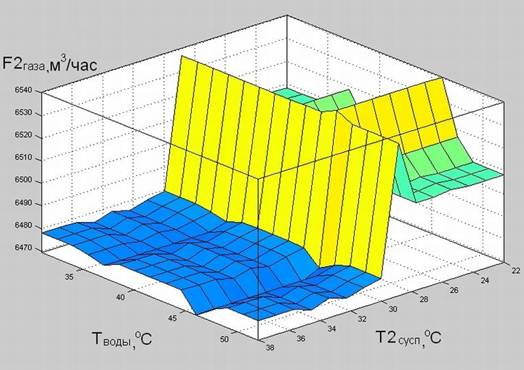
Рис. 7 – Поверхность отклика переменной: расход газа 2 входа
Выводы:
Одним из больших преимуществ использования логико-лингвистической модели является возможность непосредственного использования опыта операторов и технологов, поскольку процесс карбонизации протекает по-разному в каждой карбонизационной колонне и на основании этого опыта можно с помощью модели прогнозировать протекание процесса.
Предлагаемую модель можно использовать для управления колонной в режиме реального времени, разработки экспертной системы управления процессом, а так же в качестве программы-тренажёра для обучения технологического персонала.
СПИСОК ЛИТЕРАТУРЫ:
1 Шокин И.Н., Крашенинников С.А. Технология соды. М.: «Химия», 1975. – 288 с.
2 Верёвкин А.П. Кирюшин О.В. Теория систем: Учеб. пособие. – Уфа: Изд-во УГНТУ, 2003 – 100 с.
3 Ахметов С.А., Ишмияров М.Х., Веревкин А.П., Докучаев Е.С., Малышев Ю.М. Технология, экономика и автоматизация процессов переработки нефти и газа. – М.: Химия 2005. – 735 с.
4 Куликов Г.Г., Брейкин Т.В., Арьков В.Ю. Интеллектуальные информационные системы: Учеб. пособие / УГАТУ. – Уфа, 1999. – 129 с.
5 Круглов В.В., Дли М.И., Голунов Р.Ю. Нечёткая логика и искусственные нейронные сети. Учеб. пособие. – М.: Издательство Физико-математической литературы, 2001. – 224 с.
6 Лукас В.А. Основы фази-управления: Учебное пособие. – Екатеринбург: Изд-во УГГГА, 2000. – 62 с.
Публикации с ключевыми словами: карбонизация, логико-лингвистическая модель
Публикации со словами: карбонизация, логико-лингвистическая модель
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



