научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#1 январь 2007
![]()
Донакова Анна Александровна
средняя школа № 75, 11 класс
Научный руководитель:
Лазарева Наталия Леонидовна,
кандидат технических наук,
доцент кафедры «Оптико-электронные приборы научных исследований»
МГТУ им. Н.Э.Баумана
ВВЕДЕНИЕ
У каждого из нас есть в доме зеркало. Проходя мимо него, мы не задумываемся о том, что это не просто предмет быта, а еще и целая оптическая система, способная образовывать оптические изображения, отражая световые лучи.
Цель моей работы – экспериментальное и теоретическое изучение свойств зеркал различной формы: плоских, сферических и асферических, которые применяются в быту и технике. При экспериментах я использовала обычные бытовые зеркала и специальные оптические зеркала, которые мне дал руководитель.
Теоретические исследования я выполняла с помощью математических выводов формул и вычислений, а также путем графических построений хода световых лучей. Я использовала методы геометрической оптики, которые позволили изучить условия формирования оптического изображения объекта как совокупности изображений его отдельных точек и объяснить многие явления, связанные с отражением световых лучей.
Геометрическая оптика дает ответ на вопрос, как грамотно и точно построить оптическую систему для того, чтобы каждая точка объекта изображалась также в виде точки при сохранении геометрического подобия изображения объекту. Я пыталась найти и указать на источники искажений изображений, которые построены зеркалами.
Некоторые сведения о зеркалах и построении ими изображений были изучены в школе. Но это касалось только части свойств плоских и сферических зеркал. В оптических приборах часто используют не только плоские и сферические зеркала, но и асферические. Поэтому достаточно важно выявить их свойства и определить, где выгодно применять асферические зеркала вместо сферических.
При выполнении работы я пользовалась не только школьным учебником по физике, но и книгами, по которым учатся студенты-оптики. Кроме того, я использовала другие книги, статьи из журналов и материалы Internet. Важно, что проведенные исследования могут пригодиться мне при дальнейшем обучении на кафедре «Оптико-электронные приборы научных исследований».
ОТРАЖЕНИЕ СВЕТА
Еще в глубокой древности люди стали задумываться о том, по какому же принципу происходит отражение света в зеркалах. В Ш веке до нашей эры древнегреческим ученым Евклидом с помощью опыта был найден закон отражения.
Опыт Евклида достаточно прост: он поместил линейку так, чтобы ее край немного выступал над поверхностью воды, и с помощью капель, которые падали в воду, создал волны. Тогда он увидел, что у края линейки происходит отражение волн. При этом отраженные волны идут так, как будто они распространяются из точки, расположенной симметрично точке падения капель относительно отражающей поверхности (линейки). Я повторила опыт Евклида и убедилась в том, что это правда.
По сути Евклид использовал волновую теорию, которая в те времена не относилась к свету, так как волновую природу света доказали значительно позже. Сейчас всем известно, что световые волны – это электромагнитные волны. Поэтому справедливо считать, что взаимодействие световой волны с отражающей поверхностью аналогично тому, как водяные волны, взаимодействуют с преградой.
Кроме того, теперь известна связь между волновым и лучевым представлением света. Лучи – это прямые линии, которые являются нормалями к волновому фронту. Таким образом, используя лучевое представление света легко показать, где получится изображение точки объекта после отражения лучей от зеркала.
Главный закон, который объясняет действие зеркал любой формы – это закон отражения. Он формулируется так: луч падающий и луч отраженный лежат в одной плоскости с перпендикуляром к отражающей поверхности, восстановленным в точке падения луча, и угол падения равен углу отражения.
Известно, что не вся энергия падающего на зеркало луча, отражается и участвует в построении изображения. Часть энергии поглощается или рассеивается. Поэтому может оказаться, что изображение не такое яркое, как сам объект. Количество отраженного света во многом зависит другой важной характеристики зеркала – коэффициента отражения r. Коэффициент отражения – это величина, равная отношению потока отраженных лучей к падающему потоку лучей. Он вычисляется по формуле:
r = Фотр/Фпад < 1 (1)
Качественное зеркало должно иметь высокий коэффициент отражения. Большими коэффициентами отражения обладают гладкие металлические поверхности: алюминиевые – в ультрафиолетовом, видимом и инфракрасном диапазонах, серебряные – в видимом и инфракрасном, золотые – в инфракрасном. Коэффициент отражения от любого металла сильно зависит от длины волны света: с ее увеличением коэффициент отражения r возрастает. Это показано на рис. 1. Для некоторых металлов он стремится к 1.

Рис. 1. Коэффициенты отражения металлов
Коэффициент отражения характерен не только для металлов. Вы никогда не замечали, почему вечером при включенном свете, глядя в окно, мы сначала увидим свое нечеткое отражение, а лишь потом, хорошенько приглядевшись, предметы за окном? Стеклянная поверхность тоже может отражать свет. Это означает, что стекло – это тоже оптическое зеркало, у которого тоже есть свой коэффициент отражения r. Из книг следует, что отражение света от стеклянной поверхности происходит по закону Френеля. При нормальном падении лучей на стеклянную поверхность формула Френеля имеет простой вид:
r = [(n’-n)/ (n’+n)]² , (2)
где n – показатель преломления среды перед стеклом, n’ – показатель преломления стекла. В таблице 1 я представила, рассчитанные коэффициенты отражения стекла, которое сперва находилось в воздухе, а затем помещено в воду. Исследуя результаты своих вычислений, я сделала вывод: чем больше показатель преломления стекла n¢, тем больше коэффициент отражения r. Кроме того, при уменьшении разницы между показателями преломления стекла и среды, в которой это стекло находится, коэффициент отражения становится меньше.
Таблица 1
Коэффициенты отражения стекла в воздухе и в воде
|
Воздух |
n |
1 |
1 |
1 |
1 |
1 |
|
Стекло |
n’ |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
|
Коэффициенты отражения |
r |
0,02 |
0,04 |
0,05 |
0,06 |
0,07 |
|
Вода |
n |
1,3 |
1,3 |
1,3 |
1,3 |
1,3 |
|
Стекло |
n’ |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
|
Коэффициенты отражения |
r |
0,0009 |
0,0049 |
0,01 |
0,016 |
0,02 |
Стекло является диэлектриком. Из книг ясно, что коэффициенты отражения у диэлектриков значительно меньше, чем у металлов. Поэтому стеклянные зеркала покрывают металлическими покрытиями. В древности бытовые зеркала серебрили, а сейчас аллюминируют, так как это дешевле. Когда хотят достичь большого коэффициента отражения, то покрытия зеркал делают многослойными. Покрытия зеркал состоят из большого числа слоев двух диэлектриков попеременно с высоким и низким показателями преломления. Толщина каждого слоя такова, что оптическая длина пути света в нем составляет 1/4 длины волны. Нечетные слои делаются из материала с высоким n (например, сульфиды цинка, сурьмы, окислы титана, циркония, гафния, тория), а четные – из материала с низким n (фториды магния, стронция, двуокись кремния).
Коэффициенты отражения зеркал зависят не только от материала зеркала или покрытия, но и от углов падения лучей на зеркало. Однако этот вопрос я не рассматриваю.
ФОРМА ПОВЕРХНОСТЕЙ ЗЕРКАЛ
Поверхности зеркал, которые используются в быту и в оптических приборах, могут быть плоскими, сферическими и асферическими. При этом сферические и асферические зеркала бывают вогнутыми и выпуклыми. Плоские зеркала не создают увеличения и не вносят аберраций. Сферические и асферические зеркала создают увеличенные или уменьшенные изображения объектов. Размер и положение изображения зависят от параметров самого зеркала и от того, где расположен объект. Здесь изображения могут быть аберрационными, то есть искажены. Когда зеркало используется в бытовых целях, то его поверхность может иметь не очень точную форму. Это приводит к некоторым искажениям в изображении, но часто мы этого не замечаем. В комнатах смеха специально используют зеркала, поверхности которых сильно искажены. Поэтому изображения людей в зеркалах комнаты смеха очень уродливые.
Зеркала, которые устанавливают в оптические приборы, специально рассчитывают. При этом определяют такую форму поверхности каждого зеркала, которая позволит получить изображение нужного размера, причем без искажений. Затем стараются изготовить поверхность зеркала абсолютно точно. В книгах сказано, что максимально допустимая величина неровностей поверхностей зеркал определяется назначением зеркала: для астрономических и некоторых лазерных зеркал она не должна превышать 0,1 длины волны излучения. Для прожекторных или конденсаторных зеркал неровности могут достигать 10 длин волн.
Рассмотрю свойства различных зеркал и области их применения.
ПЛОСКИЕ ЗЕРКАЛА
Сначала рассмотрю плоские зеркала. Здесь легко заметить, что изображение объекта всегда получается в натуральную величину. При этом оно расположено как бы за зеркалом, на таком же расстоянии от зеркала, как и сам объект. Если там, где по нашему мнению находится изображение, поставить экран и посмотреть на него, то будет ясно, что на экране ничего нет. Такое изображение называют мнимым. Его можно видеть глазом, но нельзя зафиксировать на какой-либо приемник излучения. Когда такое изображение хотят зафиксировать, то его проецируют на приемник излучения с помощью какой-нибудь дополнительной оптической системы. Например, такой системой может быть хрусталик глаза. Он проецирует изображение на сетчатку, которая и является приемником излучения.
Используя графическое построение, я нашла изображение объекта АВ в плоском зеркале. Это показано на рис. 2.

Рис. 2. Изображение объекта в плоском зеркале
Здесь я применяла известный прием лучевой оптики: из точек объекта на зеркало было направлено по два луча. Лучи, вышедшие из точки А объекта, отразились от зеркала по закону отражения. Сами отраженные лучи не пресеклись между собой. Пересечься смогли только их мнимые продолжения, которые показали, где находится изображение точки А. Из построения видно, что расстояние (–s) от зеркала до точки А по абсолютной величине равно расстоянию (s’) от зеркала до точки A’ .Это свойство объекта и изображения хорошо использовать тогда, когда нужно строить изображение объекта в сложной оптической системе. Нет смысла рисовать лучи, так как можно просто откладывать равные отрезки от поверхности плоского зеркала в нужную сторону.
Далее я строила изображения в системе, состоящей из двух зеркал. Прежде всего, я поставила два зеркала параллельно друг другу, а объект расположила точно посередине между ними, как это показано на рис. 3 .

Рис. 3. Изображение объекта в двух параллельных плоских зеркалах
Так обычно девушки ставят зеркала при гадании на святках. Между зеркалами ставят свечи. Когда девушка смотрит в эти зеркала, то видит длинный коридор со свечами, так как получается бесконечное множество изображений свечей. Каждое первичное изображение здесь становится объектом для другого зеркала. Так как объект как бы постепенно удаляется от зеркала, то и его изображения также становятся все дальше и дальше. Далекие изображения становятся тускнее тех, которые близко. Это происходит потому, что коэффициент отражения зеркала меньше единицы. В таблицу 2 я поместила результаты вычислений, которые были сделаны с учетом формулы (1). Когда происходит отражение от k одинаковых зеркал, то многократно отраженный световой поток связан с падающим потоком такой формулой:
Фотр = rk Фпад. (3)
Таблица 2
Световой поток после отражения от множества зеркал
|
Число отражений |
k |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Отраженный световой поток |
Фотр, отн.ед. |
0,9 |
0,81 |
0,73 |
0,65 |
0,59 |
0,53 |
0,48 |
0,43 |
Если принять Фпад = 1, а коэффициент одного зеркала взять r = 0,9, то становится ясно, почему каждое последующее изображение тускнее предыдущего. Расчеты показали, что после 22 отражений световой поток, который попадет в глаз наблюдателя, в 10 раз меньше того, который упал на первое зеркало. При экспериментальной проверке, где я использовала два плоских бытовых зеркала, достаточно хорошо было видно только 29 изображений свечи.
Следующий эксперимент, который я провела с двумя плоскими бытовыми зеркалами, это наблюдение предмета в зеркалах, установленных под разными углами друг к другу. Предмет (свеча) всегда стоял точно посередине между зеркалами. Угол между зеркалами я устанавливала по транспортиру. Установив по совету руководителя углы 30°, 45°, 60° и 90 °, я увидела, что количество видимых изображений свечи уменьшается по мере увеличения угла между зеркалами. Результаты наблюдений даны в таблице 3.
Таблица 3
Число изображений двух наклонных зеркалах
|
Угол между зеркалами, град |
30 |
45 |
60 |
90 |
|
Число видимых изображений в каждом из зеркал |
5 |
4 |
3 |
2 |
Далее я
строила изображения точки А в двух зеркалах, которые были наклонены друг к
другу на указанные углы. Всегда оказывался тот же результат, который дан в
таблице 1. На рис. 4 для примера я показала построение изображений в зеркалах,
которые стоят под углом 45°. 
Рис. 4. Изображение объекта в двух наклонных плоских зеркалах
Как следует из книг, плоские зеркала в оптических приборах часто применяют для того, чтобы повернуть оптическую ось на какой-нибудь угол. Важно, что они строят изображение объекта в натуральную величину. Иногда плоские зеркала делают полупрозрачными, то есть наносят на них покрытие, которое имеет коэффициент отражения r =0,5. Такие зеркала половину энергии отражают, а половину пропускают насквозь. Поэтому их называют светоделительными.
СФЕРИЧЕСКИЕ ЗЕРКАЛА
Когда нужно получить увеличенное или уменьшенное изображение объекта, то часто используют сферические зеркала. В быту часто используют вогнутые сферические зеркала для бритья и нанесения косметики. Кроме того, вогнутые сферические зеркала стоят в фарах автомобилей, а выпуклые используются в качестве панорамного зеркала заднего вида.
Сферическое зеркало фокусирует падающие на него из бесконечности лучи в точку F, которая называется его фокусом. Важной характеристикой сферического зеркала является его фокусное расстояние fо – расстояние от вершины зеркала до точки F.
Сферические зеркала разделяют на вогнутые (собирающие) и выпуклые (рассеивающие). Во всех случаях это часть шара с некоторым радиусом кривизны. В оптике принято считать, что свет распространяется слева направо, тогда радиус кривизны r вогнутого зеркала будет иметь знак «–», а выпуклого «+». Фокусное расстояние сферического зеркала определяется по известной формуле:
fо = r/2 (4)
Если зеркало вогнутое, то радиус его кривизны отрицательный и фокусное расстояние также отрицательное. Выпуклое зеркало имеет положительный радиус и положительное фокусное расстояние.
Каждое сферическое зеркало ограничено, то есть обладает световым диаметром. Отношение светового диаметра к фокусному расстоянию (D: fо) называется относительным отверстием зеркала. В книгах написано, что зеркала с большими относительными отверстиями называют светосильными. Такие зеркала очень полезны, поскольку принимают на себя большие световые потоки. Но большим недостатком сферических зеркал являются аберрации, которые растут вместе с увеличением относительного отверстия. Поэтому не всегда можно применять светосильные сферические зеркала.
При изучении сферических зеркал, прежде всего, я рассмотрела, какие изображения строят вогнутые и выпуклые сферические зеркала, а затем уже исследовала их аберрации. Оптическая сила сферических зеркал обратно пропорциональна их фокусным расстояниям. Поэтому зеркала с малыми значениями радиусов поверхностей обладают большой оптической силой, а пологие зеркала – малой оптической силой. Оптическая сила создает эффект увеличения или уменьшения изображения по отношению к объекту. Кроме того, изображение в сферическом зеркале может быть не только мнимым, но и действительным. Положение изображения и его размер зависят от двух величин: от радиуса кривизны зеркала и от удаления объекта от зеркала. Формула, которая связывает удаление предмета (s), удаление изображения (s’) и радиус кривизны зеркала (r), имеет вид:
1/ s’ + 1/ s = 2 / r (5)
Из этой формулы следует, что одно и то же зеркало с постоянным радиусом r при разных s создаст разные s’. Для проверки этого факта я вычислила положения изображений в вогнутом и выпуклом зеркалах при разных удалениях объекта. Для этого формулу (5) я преобразовала к виду:
s’ = (r s)/ (2s – r) (6)
Увеличение, создаваемое зеркалом, определяется по известной формуле:
b = –s’/ s =у’/у (7)
Если увеличение положительно, то изображение получается прямым. При отрицательном увеличении изображение перевернуто.
Для анализа изображений, которые могут быть получены с помощью вогнутого и выпуклого зеркал с одинаковым по абсолютной величине радиусами кривизны, я провела вычисления по формулам, которые даны выше. Результаты вычислений представлены в таблице 4.
Из таблицы 4 видно, что при вогнутом зеркале изображение может получиться либо мнимым, либо действительным. Причем действительным оно становится, когда объект расположен в фокусе или перед ним. Когда объект между фокусом и вогнутым зеркалом, то его изображение мнимое. В выпуклом зеркале изображение всегда мнимое.
Чтобы убедиться в правильности расчетных данных из таблицы 4, я выполнила построения лучей, которые вышли из верхней точки одного и того же объекта и отразились от вогнутого и выпуклого зеркал. Зеркала были нарисованы в натуральную величину, то есть с радиусами кривизны по 100 мм. Там же были нанесены точки: С – центр кривизны, F – фокус зеркала и О – вершина зеркала. Эти точки нужны для того, чтобы через них проходили лучи, строящие изображение.
Таблица 4
Изображения в сферических зеркалах
|
Зеркала |
Расстояние s , мм |
-30 |
-50 |
-100 |
-150 |
-300 |
|
Вогнутое |
Расстояние s’, мм |
75 |
¥ |
-100 |
-75 |
-60 |
|
зеркало с r = -100 мм |
Вид изображения |
Мнимое |
Действит |
Действит |
Действит |
Действит |
|
|
Увеличение |
+2,5 |
¥ |
-1 |
-0,5 |
-0,2 |
|
Выпуклое |
Расстояние s’, мм |
18,75 |
25 |
33,33 |
37,5 |
42,86 |
|
зеркало с r = +100 мм |
Вид изображения |
Мнимое |
Мнимое |
Мнимое |
Мнимое |
Мнимое |
|
|
Увеличение |
+0,625 |
+0,5 |
+0,333 |
+0,25 |
+0,141 |
Для построения изображений удобно применять лучи, ход которых заранее известен. Это следующие лучи:
1) луч, падающий на зеркало параллельно оптической оси, после отражения приходит в фокус (F);
2) луч, падающий на зеркало через фокус (F), после отражения идет параллельно оптической оси;
3) луч, падающий на зеркало из его центра (С) кривизны, отражается обратно по своему же направлению;
4) луч, падающий в вершину (О) зеркала, отражается под углом отражения, равным углу падения.
На рисунке 5 показано построение изображений одного и того же объекта, который стоит перед вогнутым сферическим зеркалом на разных расстояниях: s = -100 мм и s = -30 мм. Первое изображение действительное, перевернутое, равное по размеру объекту, а второе изображение – мнимое, увеличенное и прямое. Все это полностью соответствует данным таблицы 4.

Рис. 5. Изображение объектов в вогнутом зеркале
На рисунке 6 дано построение изображений одного и того же объекта, стоящего перед выпуклым сферическим зеркалом, на расстояниях s = -30 мм и s = -100 мм. Оба изображения оказались мнимыми, прямыми и уменьшенными, что соответствует данным таблицы 4.

Рис. 6. Изображение объектов в выпуклом зеркале
В книге [1] написано, что сферические зеркала искажают изображения объектов. Когда зеркало светосильное, то лучи, которые падают на зеркало на большой высоте, после отражения не приходят в ту же точку, куда пришли лучи, отраженные на малой высоте. Исключение составляют только лучи, которые прошли через центр кривизны (С), так как они являются нормалями к зеркалу. Все остальные лучи изображают точку в виде пятна рассеяния, что портит изображение объекта.
Очень часто сферические зеркала применяют для фокусировки лучей, которые падают на зеркало параллельно оптической оси. Для выяснения, куда придут лучи, отраженные от вогнутого и выпуклого сферических зеркал с радиусами кривизны r = -100 мм и r =100 мм, я взяла по три луча, которые упали на зеркала на высотах у1 = 20 мм; у2 =50 мм и у3 = 70 мм. Затем по совету руководителя я записала уравнение меридионального сечения сферической поверхности в виде, как принято записывать уравнение асферических поверхностей второго порядка:
y2 + а1z + а2z2 = 0 (8)
При такой записи уравнения вершина поверхности в начале декартовой системы координат, ось z – ось симметрии. Коэффициенты уравнения (8) связаны с параметрами поверхностей (ro – радиусом кривизны при вершине поверхности, е – эксцентриситетом) следующими формулами:
a1= - 2ro, (9)
a2 = - (e2-1) (10)
Так как у сферы эксцентриситет равен нулю, то а2 =1 и уравнение сферы будет:
y2 - 2r z + z 2 = 0. (11)
У сферы нет радиуса при вершине, есть просто радиус. Поэтому в уравнении сферы ro я заменила на r.
Затем из книги [1] я взяла формулу, по которой вычисляется угол между нормалью к точке кривой второго порядка и осью z:
tg j = y / (0,5 a1 + a2 z) (12)
Удаление фокуса от вершины сферической поверхности я вычисляла по формуле:
f = [y / tg (2 j)] + z (13)
Для удобства вычислений по формулам я составила файл для программы EXCEL. Распечатку этого файла назвала таблицей 5. Из последнего столбца этой таблицы видно, что лучи, отраженные от вогнутой и выпуклой сфер, пересекают оптическую ось далеко друг от друга. Если сравнить фокусные расстояния, вычисленные по формуле (4) (для вогнутого зеркала fо = - 50 мм, а для выпуклого зеркала fо = 50 мм), то становится ясно следующее: с увеличением высоты луча на поверхностях обоих зеркал разница между значениями, вычисленными по формуле (4), растет. Поэтому в плоскости, где находится точка F, лучи образуют не точку, а пятно рассеяния.
Таблица 5
Расчет хода лучей, отраженных от сфер
|
Формулы для расчета |
|
|||||||||||||
|
|
|
|
z1=(-a1+sqrt(a1*a1-4*a2*y*y))/(2*a2) |
z2=(-a1-sqrt(a1*a1-4*a2*y*y))/(2*a2) |
|
|||||||||
|
a1=-2*ro |
a2=-(e*e-1) |
|
|
tgф=2*y/(a1+2*a2*z) |
t=-y/tg(2ф) |
f=t+z |
|
|||||||
|
Исходные данные |
Вычисленные величины |
|
||||||||||||
|
ro,мм |
e |
y,мм |
a1 |
a2 |
z1,мм |
tgф |
ф, рад |
2ф, рад |
tg(2ф) |
t,мм |
f,мм |
|
||
|
-100 |
0 |
20 |
200 |
1 |
-2,0204 |
0,20412 |
0,20136 |
0,40272 |
0,426 |
-46,949 |
-48,969 |
|
||
|
-100 |
0 |
50 |
200 |
1 |
-13,397 |
0,57735 |
0,5236 |
1,0472 |
1,73205 |
-28,868 |
-42,265 |
|
||
|
-100 |
0 |
70 |
200 |
1 |
-28,586 |
0,9802 |
0,7754 |
1,55079 |
49,99 |
-1,4003 |
-29,986 |
|
||
|
Исходные данные |
Вычисленные величины |
|
||||||||||||
|
ro,мм |
e |
y,мм |
a1 |
a2 |
z2,мм |
tgф |
ф, рад |
2ф, рад |
tg(2ф) |
t,мм |
f,мм |
|
||
|
100 |
0 |
20 |
-200 |
1 |
2,02041 |
-0,2041 |
-0,2014 |
-0,4027 |
-0,426 |
46,9486 |
48,969 |
|
||
|
100 |
0 |
50 |
-200 |
1 |
13,3975 |
-0,5774 |
-0,5236 |
-1,0472 |
-1,7321 |
28,8675 |
42,265 |
|
||
|
100 |
0 |
70 |
-200 |
1 |
28,5857 |
-0,9802 |
-0,7754 |
-1,5508 |
-49,99 |
1,40028 |
29,986 |
|
||
По данным таблицы 5 я построила ход лучей, отраженных от вогнутого и выпуклого зеркал. Это показано на рис. 7.

Рис. 7. Абберация лучей, отраженных от сферы
Оказалось, что угол между оптической осью зеркала и лучом, который упал на зеркало на высоте у = 70 мм, очень большой: он равен 89° (tg (2 j)= 49,9). Поэтому это луч после отражения пойдет почти перпендикулярно оптической оси.
Из книг следует, что разность между f и fo и называется продольной сферической аберрацией Ds’ (лат. – уклонение):
Ds’ = f - fo (14)
Диаметр пятна рассеяния, которое получилось в фокальной плоскости сферического зеркала легко определить по формуле:
Dп = 2 Ds’ tg (2j) (15)
По формуле (15) я вычислила диаметры пятен для обоих зеркал, результаты вычислений даны в таблице 6.
Таблица 6
Диаметры пятен рассеяния и волновые аберрации при фокусировке параллельных лучей сферическими зеркалами
|
|
Вогнутое зеркало с r = -100 мм |
Выпуклое зеркало с r = +100 мм |
||||
|
у, мм |
20 |
50 |
70 |
20 |
50 |
70 |
|
Ds’, мм |
1,03 |
7,74 |
20,01 |
-1,03 |
-7,74 |
-20,01 |
|
tg (2j) |
-0,426 |
-1,732 |
-49,99 |
0,426 |
1,732 |
49,99 |
|
Dп, мм |
0,88 |
26,4 |
2001,0 |
0,88 |
26,4 |
2001,0 |
|
l, мкм |
39,18 |
1331,7 |
3631,6 |
39,18 |
1331,7 |
3631,6 |
Из таблицы 6 видно, что в моем случае пятна рассеяния имеют слишком большие диаметры. Особенно это касается лучей, падающих на зеркала на высоте 70 мм: здесь пятна просто гигантские. По совету руководителя я рассчитала ход этих лучей по программе «Призма», которая используется для оптических расчетов. Результаты подтвердились. Кроме того, программа «Призма» вычислила волновые аберрации, которые я представила в последней строке таблицы 6. Они также оказались слишком большими.
Увидев тенденцию увеличения аберраций, я вновь рассчитала ход лучей по программе «Призма», уменьшив высоты лучей, которые падали на эти зеркала. При этом я стремилась к тому, чтобы волновые аберрации не превышали 0,05 мкм, что соответствует идеальной оптической системе. Результаты расчета даны в таблице 7.
Таблица 7
Диаметры пятен рассеяния и волновые аберрации при фокусировке параллельных лучей, идущих на малых высотах, сферическими зеркалами
|
|
Вогнутое зеркало с r = -100 мм |
Выпуклое зеркало с r = +100 мм |
||||
|
у, мм |
3 |
5 |
10 |
3 |
5 |
10 |
|
Ds’, мм |
0,022 |
0,062 |
0,252 |
-0,022 |
-0,062 |
-0,252 |
|
tg (2j) |
-0,06 |
-0,1 |
-0,2 |
0,06 |
0,1 |
0,2 |
|
Dп, мм |
0,0028 |
0,013 |
0,1 |
0,0028 |
0,013 |
0,1 |
|
l, мкм |
0,02 |
0,156 |
2,49 |
0,02 |
0,156 |
2,49 |
Результаты в таблице 7 показали, что поставленному условию по волновым аберрациям удовлетворяет только луч, идущий на высоте у = 3 мм. Поэтому можно заключить, что практически безаберрационное изображение построит сферическое зеркало диаметром D = 6 мм, при фокусном расстоянии fо = 50 мм: его относительное отверстие будет очень малым D: f = 1:8.
АСФЕРИЧЕСКИЕ ЗЕРКАЛА
В книге [3] я прочитала, что для улучшения изображения выгодно зеркала делать асферическими. Поэтому я рассмотрела, ход лучей, отраженных от асферических зеркал второго порядка: параболического, эллиптического и гиперболического. Нужно было выявить, какой формы зеркало лучше всего фокусирует пучок лучей, параллельных оптической оси. Я рассматривала вогнутые и выпуклые аферические зеркала, направляя на них те же лучи, что и на сферические зеркала.
Здесь я не рассматривала, где и какие получаются изображения, так как формулы с (4) по (7) верны не только для сферических зеркал, но и для асферических. Поэтому результаты, которые даны в таблице 4, годятся и для асферических зеркал.
Формулы с (8) по (15) также подходят для расчетов по асферическим зеркалам. Отличительной особенностью асферических зеркал от сфер будет то, что у сферы эксцентриситет равен нулю, а у асферических поверхностей эксцентриситеты ненулевые. У параболоидов эксцентриситет всегда е =1. Эллипсоиды имеют эксцентриситеты 0< е < 1. Гиперболоиды имеют эксцентриситеты е >1. Для вычислений руководитель предложил мне выбрать следующие значения эксцентриситетов: для эллипсоида е =0,9, для гиперболоида е = 1,1. Радиусы кривизны при вершинах всех асферических зеркал было предложено взять: для вогнутых ro = -100 мм, для выпуклых ro = 100 мм. Высоты лучей на асферических поверхностях выли выбраны такие же, как у сферических зеркал: у1= 20 мм,. у2= 50 мм, у3= 70 мм.
Чтобы построить ход лучей, отраженных от асферических зеркал, пришлось вычислять координаты меридиональных сечений асферических поверхностей, а также углы наклона нормалей и углы, которые составляют отраженные лучи с оптической осью. Для этого я записала уравнения меридиональных сечений всех предложенных зеркал, находила корни этих уравнений, а затем применяла программу EXCEL. Результаты вычислений даны в таблицах 8, 9 и 10.
Таблица 8
Расчет хода лучей, отраженных от параболоидов
|
Формулы для расчета |
|||||||||||
|
a1=-2*ro |
|
a2=-(e*e-1) |
z=y*y/(2*ro) |
tgф=2*y/(a1+2*a2*z) |
|
t=-y/tg(2ф) |
f=t+z |
||||
|
Исходные данные |
Вычисленные величины |
||||||||||
|
ro,мм |
e |
y,мм |
a1 |
a2 |
z,мм |
tgф |
ф, рад |
2ф, рад |
tg(2ф) |
t,мм |
f,мм |
|
-100 |
1 |
20 |
200 |
0 |
-2 |
0,2 |
0,197396 |
0,394791 |
0,416667 |
-48 |
-50 |
|
-100 |
1 |
50 |
200 |
0 |
-12,5 |
0,5 |
0,463648 |
0,927295 |
1,333333 |
-37,5 |
-50 |
|
-100 |
1 |
70 |
200 |
0 |
-24,5 |
0,7 |
0,610726 |
1,221452 |
2,745098 |
-25,5 |
-50 |
|
Исходные данные |
Вычисленные величины |
||||||||||
|
ro,мм |
e |
y,мм |
a1 |
a2 |
z,мм |
tgф |
ф, рад |
2ф, рад |
tg(2ф) |
t,мм |
f,мм |
|
100 |
1 |
20 |
-200 |
0 |
2 |
-0,2 |
-0,1974 |
-0,39479 |
-0,41667 |
48 |
50 |
|
100 |
1 |
50 |
-200 |
0 |
12,5 |
-0,5 |
-0,46365 |
-0,9273 |
-1,33333 |
37,5 |
50 |
|
100 |
1 |
70 |
-200 |
0 |
24,5 |
-0,7 |
-0,61073 |
-1,22145 |
-2,7451 |
25,5 |
50 |
Таблица 9
Расчет хода лучей, отраженных от эллипсов
|
Формулы для расчета |
|||||||||||||
|
|
z1=(-a1+sqrt(a1*a1-4*a2*y*y))/(2*a2) |
z2=(-a1-sqrt(a1*a1-4*a2*y*y))/(2*a2) |
|
||||||||||
|
a1=-2*ro |
a2=-(e*e-1) |
|
tgф=2*y/(a1+2*a2*z) |
|
t=-y/tg(2ф) |
f=t+z |
|||||||
|
Исходные данные |
Вычисленные величины |
||||||||||||
|
ro,мм |
e |
y,мм |
a1 |
a2 |
z1,мм |
tgф |
ф, рад |
2ф, рад |
tg(2ф) |
t,мм |
f,мм |
||
|
-100 |
0,9 |
20 |
200 |
0,2 |
-2,00381 |
0,200764 |
0,19813 |
0,396261 |
0,418393 |
-47,802 |
-49,8058 |
||
|
-100 |
0,9 |
50 |
200 |
0,2 |
-12,6521 |
0,512316 |
0,473451 |
0,946903 |
1,389268 |
-35,9902 |
-48,6422 |
||
|
-100 |
0,9 |
70 |
200 |
0,2 |
-25,0984 |
0,735052 |
0,633866 |
1,267732 |
3,197981 |
-21,8888 |
-46,9872 |
||
|
Исходные данные |
Вычисленные величины |
||||||||||||
|
ro,мм |
e |
y,мм |
a1 |
a2 |
z2,мм |
tgф |
ф, рад |
2ф, рад |
tg(2ф) |
t,мм |
f,мм |
||
|
100 |
0,9 |
20 |
-200 |
0,2 |
2,003815 |
-0,20076 |
-0,19813 |
-0,39626 |
-0,41839 |
47,80199 |
49,80581 |
||
|
100 |
0,9 |
50 |
-200 |
0,2 |
12,65207 |
-0,51232 |
-0,47345 |
-0,9469 |
-1,38927 |
35,99017 |
48,64224 |
||
|
100 |
0,9 |
70 |
-200 |
0,2 |
25,09843 |
-0,73505 |
-0,63387 |
-1,26773 |
-3,19798 |
21,88881 |
46,98725 |
||
Таблица 10
Расчет хода лучей, отраженных от гиперболоида
|
|
|
|
Формулы для расчета |
|
|
|
|
|
|||
|
|
|
z1=(-a1+sqrt(a1*a1-4*a2*y*y))/(2*a2) |
z2=(-a1-sqrt(a1*a1-4*a2*y*y))/(2*a2) |
|
|||||||
|
a1=-2*ro |
a2=-(e*e-1) |
|
tgф=2*y/(a1+2*a2*z) |
t=-y/tg(2ф) |
f=t+z |
||||||
|
Исходные данные |
Вычисленные величины |
||||||||||
|
ro,мм |
e |
y,мм |
a1 |
a2 |
z1,мм |
tgф |
ф, рад |
2ф, рад |
tg(2ф) |
t,мм |
f,мм |
|
-100 |
1,1 |
20 |
200 |
-0,2 |
-1,99582 |
0,199165 |
0,196593 |
0,393186 |
0,414784 |
-48,2179 |
-50,2137 |
|
-100 |
1,1 |
50 |
200 |
-0,2 |
-12,3401 |
0,48737 |
0,453493 |
0,906986 |
1,278398 |
-39,1115 |
-51,4516 |
|
-100 |
1,1 |
70 |
200 |
-0,2 |
-23,9002 |
0,666546 |
0,587919 |
1,175838 |
2,398869 |
-29,1804 |
-53,0806 |
|
Исходные данные |
Вычисленные величины |
||||||||||
|
ro,мм |
e |
y,мм |
a1 |
a2 |
z2,мм |
tgф |
ф, рад |
2ф, рад |
tg(2ф) |
t,мм |
f,мм |
|
100 |
1,1 |
20 |
-200 |
-0,2 |
1,995818 |
-0,19917 |
-0,19659 |
-0,39319 |
-0,41478 |
48,21791 |
50,21373 |
|
100 |
1,1 |
50 |
-200 |
-0,2 |
12,34011 |
-0,48737 |
-0,45349 |
-0,90699 |
-1,2784 |
39,11146 |
51,45156 |
|
100 |
1,1 |
70 |
-200 |
-0,2 |
23,90022 |
-0,66655 |
-0,58792 |
-1,17584 |
-2,39887 |
29,18042 |
53,08064 |
1. Парабола
Уравнение параболы имеет вид: y² – 2roz = 0.
При моих исходных данных для вогнутой параболы: y² + 200 z = 0, для выпуклой параболы: y² – 200 z = 0.
Корни уравнения параболы легко определить по формуле: z = y2 / (2 ro).
Углы наклона нормалей к параболам определяются по формуле: tg j = y / (ro).
2. Эллипс
Уравнение эллипса имеет вид: y² – 2roz – (e² – 1)z²=0.
При моих исходных данных для вогнутого эллипса: y² + 200 z +0,19 z2 = 0, для выпуклого эллипса: y² – 200 z +0,19 z2 = 0.
Корни уравнения эллипса определяю по формуле: z1,2 = {ro±Ö[ ro2+ (e2–1)у2]}/(e2–1).
При расчетах выяснилось, что физический смысл для вогнутого эллипса имеет корень z1, а для выпуклого – корень z2.
Углы наклона нормалей к эллипсам определяются по формуле: tg j = -y/[ro+ (e2–1) z].
3. Гипербола
Уравнение гиперболы имеет вид: y² – 2roz – (e² – 1)z²=0.
При моих исходных данных для вогнутой гиперболы: y² + 200 z –0,21 z2 = 0, для выпуклой гиперболы: y² – 200 z +0,21 z2 = 0.
Корни уравнения эллипса определяю по формуле: z1,2 = {ro±Ö[ ro2+ (e2–1)у2]}/(e2–1).
При расчетах выяснилось, что физический смысл для вогнутой гиперболы имеет корень z1, а для выпуклой – корень z2.
Углы наклона нормалей к эллипсам определяются по формуле: tg j = -y / [ro+ (e2–1) z].
Проанализировав результаты, представленные в таблицах 8, 9 и 10, я сделала такие выводы:
1) отражающий параболоид не вносит аберрацию в пучок лучей, которые падают на него параллельно оптической оси: все лучи фокусируются в одной и той же точке F, удаленной от вершины параболоида на расстояние fo, которое вычислено по формуле (4);
2) отражающие эллипсоид и гиперболоид при таком же ходе лучей аберрации вносят, так как фокусные расстояния для разных лучей отличаются друг от друга и от расстояния fo, которое вычислено по формуле (4);
3) величины аберраций эллипсоида и гиперболоида значительно меньше, чем у сферы (см. таблицу 5).
По результатам из таблиц 8, 9 и 10 я построила ход лучей, отраженных от вогнутых и выпуклых параболоидов, эллипсоидов и гиперболоидов. Это показано на рис.8, 9 и 10.

Рис. 8. Абберация лучей, отраженных от параболоида
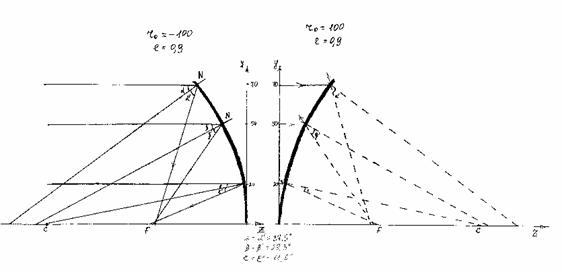
Рис. 9. Абберация лучей, отраженных от эллипсоида
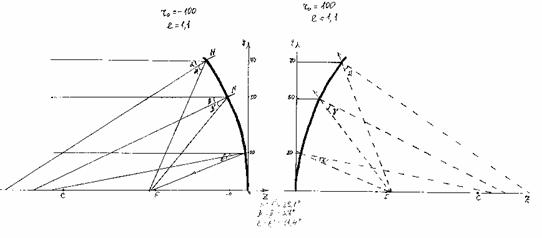
Рис. 10. Абберация лучей, отраженных от гиперболоида
Пользуясь программой «Призма» я вычислила аберрации лучей при отражении от параболоида, эллипсоида и гиперболоида. Результаты даны в таблицах 11, 12 и 13.
Таблица 11
Диаметры пятен рассеяния и волновые аберрации при фокусировке параллельных лучей параболическими зеркалами
|
|
Вогнутое зеркало с rо = -100 мм |
Выпуклое зеркало с rо = +100 мм |
||||
|
у, мм |
20 |
50 |
70 |
20 |
50 |
70 |
|
Ds’, мм |
0 |
0 |
0 |
0 |
0 |
0 |
|
tg (2j) |
-0,417 |
-1,333 |
-2,745 |
0,417 |
1,333 |
2,745 |
|
Dп, мм |
0 |
0 |
0 |
0 |
0 |
0 |
|
l, мкм |
0 |
0 |
0 |
0 |
0 |
0 |
Таблица 12
Диаметры пятен рассеяния и волновые аберрации при фокусировке параллельных лучей эллиптическими зеркалами
|
|
Вогнутое зеркало с rо = -100 мм |
Выпуклое зеркало с rо = +100 мм |
||||
|
у, мм |
20 |
50 |
70 |
20 |
50 |
70 |
|
Ds’, мм |
0,194 |
1,358 |
3,013 |
-0,194 |
-1,358 |
-3,013 |
|
tg (2j) |
-0,418 |
-1,389 |
-3,198 |
0,418 |
1,389 |
3,198 |
|
Dп, мм |
0,162 |
3,772 |
19,271 |
0,162 |
3,772 |
19,271 |
|
l, мкм |
7,333 |
240,72 |
772,75 |
7,333 |
240,72 |
772,75 |
Таблица 13
Диаметры пятен рассеяния и волновые аберрации при фокусировке параллельных лучей гиперболическими зеркалами
|
|
Вогнутое зеркало с rо = -100 мм |
Выпуклое зеркало с rо = +100 мм |
||||
|
у, мм |
20 |
50 |
70 |
20 |
50 |
70 |
|
Ds’, мм |
0,214 |
1,452 |
3,081 |
-0,214 |
-1,452 |
-3,081 |
|
Tg (2j) |
-0,415 |
-1,278 |
-2,399 |
0,415 |
1,278 |
2,399 |
|
Dп, мм |
0,177 |
3,711 |
14,782 |
0,177 |
3,711 |
14,782 |
|
l, мкм |
8,046 |
258,52 |
832,66 |
8,046 |
258,52 |
832,66 |
Из таблицы 11 видно, параболоид не вносит аберраций в лучи, которые идут даже на больших высотах. Это согласуется с данными из книг [1] и [3]. Поэтому параболические зеркала выгодно использовать для фокусировки пучков световых лучей большого диаметра. Часто вогнутые параболические зеркала применяют в качестве объективов телескопов.
Данные таблиц 12 и 13 говорят о том, что эллиптические и гиперболические зеркала вносят аберрации. Если сравнить эти аберрации с данными таблицы 6, то можно сделать вывод: они значительно меньше, чем аберрации сферических зеркал. Чтобы выявить, при каких относительных отверстиях эллиптические и гиперболические зеркала окажутся идеальными, я сделала вычисления хода лучей по программе «Призма». При этом высоты лучей, которые упали на эллиптическое и гиперболическое зеркала были небольшими. Результаты даны в таблицах 14 и 15. Здесь ясно видно, что эти зеркала практически идеальны при относительном отверстии D: fo = 1: 5.
Таблица 14
Диаметры пятен рассеяния и волновые аберрации при фокусировке параллельных лучей, идущих на малых высотах, эллиптическими зеркалами
|
|
Вогнутое зеркало с rо = -100 мм |
Выпуклое зеркало с rо = +100 мм |
||||
|
у, мм |
3 |
5 |
10 |
3 |
5 |
10 |
|
Ds’, мм |
0,0043 |
0,0119 |
0,0478 |
-0,0043 |
-0,0119 |
-0,0478 |
|
Tg (2j) |
-0,0601 |
-0,100 |
-0,202 |
0,0601 |
0,100 |
0,202 |
|
Dп, мм |
0,0006 |
0,0024 |
0,020 |
0,0006 |
0,0024 |
0,020 |
|
l, мкм |
0,0038 |
0,0296 |
0,471 |
0,0038 |
0,0296 |
0,471 |
Таблица 15
Диаметры пятен рассеяния и волновые аберрации при фокусировке параллельных лучей, идущих на малых высотах, гиперболическими зеркалами
|
|
Вогнутое зеркало с rо = -100 мм |
Выпуклое зеркало с rо = +100 мм |
||||
|
у, мм |
3 |
5 |
10 |
3 |
5 |
10 |
|
Ds’, мм |
0,0047 |
0,0131 |
0,0528 |
-0,0047 |
-0,0131 |
-0,0528 |
|
Tg (2j) |
-0,0601 |
-0,100 |
-0,202 |
0,0601 |
0,100 |
0,202 |
|
Dп, мм |
0,0006 |
0,0026 |
0,021 |
0,0006 |
0,0026 |
0,021 |
|
l, мкм |
0,0042 |
0,033 |
0,520 |
0,0042 |
0,033 |
0,520 |
ОСНОВНЫЕ ИТОГИ РАБОТЫ
Проведено теоретическое и экспериментальное исследование основных свойств плоских, сферических и асферических зеркал. При вычислениях была использована компьютерная программа EXCEL.
В процессе работы изучены книги по оптике, освоены приемы построения хода лучей в зеркалах, а также компьютерная программа «Призма», имеющаяся на кафедре «Оптико-электронные приборы научных исследований».
Полученные результаты полезны, так как они позволили глубже понять работу оптических зеркал. Их можно использовать для демонстрации на уроках физики в школе.
Список литературы
1. Заказнов Н.П.. Кирюшин С.И., Кузичев В.И. Теория оптических систем – М.: Машиностроение, 1992.
2. Справочник конструктора оптико-механических приборов / Под ред. В.А.Панова – Л.: Машиностроение, 1980.
3. Русинов М.М. Несферические поверхности в оптике – М.: Недра, 1973.
Публикации с ключевыми словами: оптика, зеркало
Публикации со словами: оптика, зеркало
Смотри также:
- 8-я Международная специализированная выставка оборудования, технологий и материалов лазерно-оптического и электронного приборостроения LICRussia (Лазеры. Оптика. Электроника.)
- 8-я Международная специализированная выставка оборудования, технологий и материалов лазерно-оптического и электронного приборостроения LICRussia (Лазеры. Оптика. Электроника.)
- Предварительное обоснование технического облика оптической системы целевой аппаратуры для ка в составе космического сегмента СККП
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



