научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#1 январь 2007
УДК 004.3 :519.6
Иванова Г.С.
Разработка средств автоматизации решения задач структурного синтеза, в том числе и создание языка описания алгоритмов решения этих задач, невозможно без детального анализа способов задания отношений элементов моделей при их описании, поскольку описание способов задания в имеющихся источниках [1–4] не обладает достаточной полнотой и глубиной и не систематизировано.
Задание отношений смежности и инцидентности на универсумах вершин и ребер графовых моделей выполняют в матричной или аналитической форме. Обе формы позволяют описывать только двуместные отношения. В табличной форме элемент таблицы фиксирует наличие отношения R Ì A ´ B между элементом ai, сопоставленным строке i, и элементом bj, сопоставленным столбцу матрицы j, т. е. (ai, bj) Î R, aiÎ A & bj Î B. В аналитической – каждое множество описания по отношению смежности или инцидентности представляет собой совокупность образов элемента исходного множества по задаваемому отношению, т. е. Rai = {bj / aiÎ A & bj Î B & (ai, bj) Î R}.
Откуда следует, что любая из указанных форм позволяет определить смежность вершин ориентированных или неориентированных графов и мультиграфов и инцидентность вершины-ребра и ребра-вершины любой графовой модели, которые изначально двуместны.
Отношения смежности вершин гиперграфов и ультраграфов n-местны, однако, каждое из них может быть представлено как множество двуместных отношений. Так неориентированная n-местная связь (ребро гиперграфа), задаваемая множеством или мультимножеством Xnj = {xi, xk, …xr}Î Fn Ì Xn, |Xnj| = n, может рассматриваться как совокупность попарных связей вершин ребра Xj = {{xi, xk}/ xi, xk Î Xnj}. Каждая пара множества Xj представляет собой фрагмент ребра гиперграфа и является элементом симметричного бинарного отношения смежности, т. е. {xi, xk}ÎXj & {xi, xk}Î F2Ì X2, а количество таких пар равно |Xj| = n(n-1).
N-местное отношение порядка подмножеств (дуга ультраграфа), определяемое упорядоченной парой подмножеств вершин-источников Xi и вершин-приемников Xk, т. е. Xnj = (Xi, Xk) Î FnÌ Xn, | Xi | +| Xk | = n, в этом случае будет представлено как множество упорядоченных пар Xj = {(xr, xc)/ xrÎ Xi & xcÎ Xk}. Количество пар равно – |Xj| = n1n2, где n1= |Xi | £ n, n2= |Xk | £ n, откуда n1 n2 £ n2.
Ориентированная n-местная связь (дуга ориентированного гиперграфа), определяемая кортежем Xnj = (xi, xk, xc, …, xe, xr) Î FnÌ Xn, | Xnj | = n, соответственно, может рассматриваться как кортеж упорядоченных пар Xj = ((xi, xk), (xk, xc), …, (xe, xr)). Каждая упорядоченная пара кортежа Xj, представляющая собой фрагмент гипердуги, является элементом бинарного отношения смежности, т. е. (xi, xk) Î Xj & (xi, xk)Î F2Ì X2, а количество таких пар равно |Xj| = n-1.
Таким образом, для неориентированных и ориентированных гипер- и ультраграфов также, как и для графов и мультиграфов, возможно матричное и аналитическое представление через смежность при условии, что оно учитывает выявленные особенности.
Матричное задание графовых моделей в случае одного универсума предполагает задание матрицы смежности, а в случае двух универсумов – матрицы инцидентности. Элемент матрицы смежности ai,j соответствует упорядоченной паре (xi, xj). Для ориентированных и неориентированных графов этот элемент задается как
 .
.
Кратность связей мультиграфа в такой матрице может отображаться соответствующими натуральными числами:
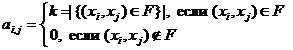 .
.
В ориентированном графе каждой связи соответствует одна упорядоченная пара, а в неориентированном – две, поскольку {xi, xj} = {(xi, xj),( xj, xi)}. Соответственно неориентированные связи в матрице смежности отображаются два раза, а ориентированные – один, следовательно, матрица смежности неориентированного графа симметрична и может быть представлена в диагональной форме.
Представление n-местных отношений неориентированного гипер- и ультраграфов через двуместные показывает, что отношения смежности вершин этих моделей также можно описать матрицей смежности, но вследствие того, что пары могут принадлежать разным отношениям, а информация об этом не отображается, такое представление не позволяет восстановить исходный граф по данному представлению. Гиперграф при таком представлении неотличим от неориентированного, а ультраграф – от ориентированного графа (см. таблицу 1).
Таблица 1 – Задание отношений матрицами смежности
|
Название модели |
Графическое представление |
Матрица смежности вершин
|
Матрица смежности ребер |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Матрица |
Условные обозначения |
Матрица |
Условные обозначения |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Неориентированный граф |
|
|
1 – если (xi, xj)ÎF; 0 – если (xi, xj)ÏF |
|
1 – если (ui, uj)ÎF; 0 – если (ui, uj)ÏF |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Гиперграф |
|
|
то же*
|
|
то же*
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Смешанный ультраграф |
|
|
то же*
|
– |
– |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Смешанный гиперграф |
|
|
то же*
|
– |
– |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Смешанный мультиграф |
|
|
k=|{(xi,xj)ÎF}|, если (xi, xj)ÎF; 0 – если (xi,xj)ÏF |
– |
– |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Смешанный ультраграф с кратными гипердугами* |
|
|
то же* |
– |
– |
||||||||||||||||||||||||||||||||||||||||||||||||||
* – не позволяет адекватно задать графовую модель.
Представление гипердуг ориентированного гиперграфа матрицей смежности требует фиксации не только наличия упорядоченной пары, но и указания ее номера в кортеже. Поскольку каждая пара может входить, и не по одному разу, в несколько ребер, причем каждый раз со своим номером, отобразить соответствующую информацию в матрице смежности без указания номера ребра невозможно. При необходимости можно построить матрицу смежности, в которой отображается информация о количестве связей каждой пары вершин, но не различаются связи в пределах ребра и связи в разных ребрах и, соответственно, не фиксируется номер пары в ребре и номер ребра. Практически в этом случае мы рассматриваем ориентированный гиперграф, как ориентированный мультиграф.
Матрица смежности ребер может быть построена только для неориентированных графовых моделей: неориентированного графа и гиперграфа, так как отношение смежности определено только для неориентированных ребер. При этом представление графа матрицей смежности ребер позволяет задать модель, но усложняет обратный переход от модели к объекту, поскольку отношение смежности ребер явно не указывает вершины, являющиеся общими для каждой пары ребер.
Матрицы смежности вершин и ребер, не позволяющие адекватно задавать графовую модель могут использоваться как вспомогательная информация, используемая для снижения вычислительной сложности некоторых операций. Например, использование матрицы смежности позволяет упростить нахождение вершин, смежных данной в гиперграфе схемы при решении задачи разрезания последовательным алгоритмом.
Поскольку отношения инцидентности вершины–ребра и ребра–вершины для рассматриваемых моделей двуместны, матрица инцидентности позволяет адекватно задавать не только графы и мультиграфы, но и гипер- и ультраграфы, причем симметричность отношений инцидентности делает достаточным определение одного из них, например, Г1 – отношения инцидентности вершины-ребра.
Для неориентированных графов и мультиграфов в матрице инциденций вершины-ребра указывают:
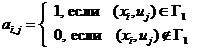 .
.
Для неориентированного гиперграфа при таком представлении возможные повторные вхождения вершин в гиперребро отображают, указывая в матрице кратность вхождения:
 .
.
Для ориентированных графов и мультиграфов матрица инцидентности должна отображать направление дуг: вершина инцидентна началу дуги, вершина инцидентна концу дуги. Соответственно для ориентированных графов множество отношений инцидентности Г1 разбивается на два ![]() – вершина инцидентна началу дуги,
– вершина инцидентна началу дуги, ![]() – вершина инцидентна концу дуги. Для смешанных графов и мультиграфов это множество разбивается уже на четыре подмножества:
– вершина инцидентна концу дуги. Для смешанных графов и мультиграфов это множество разбивается уже на четыре подмножества: ![]() – вершина инцидентна началу дуги,
– вершина инцидентна началу дуги, ![]() – вершина инцидентна концу дуги, Г(~)1 – вершина инцидентна звену, Г(о)1 – вершина инцидентна петле. Тогда элемент матрицы инцидентности смешанного графа или мультиграфа кодируется как (см. таблицу 2):
– вершина инцидентна концу дуги, Г(~)1 – вершина инцидентна звену, Г(о)1 – вершина инцидентна петле. Тогда элемент матрицы инцидентности смешанного графа или мультиграфа кодируется как (см. таблицу 2):
 .
.
Таблица 2 – Задание отношений матрицами инцидентности
|
Название модели |
Графическое представление |
Граф Кенига |
Матрица инцидентности вершины-ребра |
Условные обозначения |
|||||||||||||||||||||||||||||||||||
|
Неориентированный граф |
|
|
|
1, если (xi, uj)ÎГ1, 0, если (xi, uj)ÏГ1 |
|||||||||||||||||||||||||||||||||||
|
Гиперграф |
|
|
|
k = |{(xi, uj)}| Ì Г1, если (xi, uj) ÎГ1, 0, если (xi, uj)ÏГ1 |
|||||||||||||||||||||||||||||||||||
|
Смешанный мультиграф |
|
|
|
a, если (xi, uj)ÎГ(¬) 1; b, если (xi, uj) ÎГ(¬)1, с, если (xi, uj) ÎГ(~)1, d, если (xi, uj) ÎГ(o)1, 0, если (xi, uj)ÏГ1= = Г(¬)1 ÈГ(¬)1ÈГ(~)1ÈГ(o)1 |
|||||||||||||||||||||||||||||||||||
|
Смешанный ультраграф |
|
|
|
(<а, k1>,<b, k2>), если (xi, uj)ÎГ1, где a, если (xi,uj)ÎГ(¬)1, b, если (xi, uj)ÎГ(¬)1, ki – количество пар каждого типа, с, если (xi, uj) ÎГ(~)1; d, если (xi, uj) ÎГ(o)1; 0, если (xi, uj)ÏГ1 |
|||||||||||||||||||||||||||||||||||
|
Смешанный ультраграф с кратными дугами |
|
|
|
(<а, k1>,<b, k2>), где a, если (xi,uj)ÎГ(¬)1, b, если (xi, uj)Î Г(¬)1, <с,k3>,если(xi,uj)ÎГ(~) 1; <d,k4>,если (xi,uj)ÎГ(o)1; ki – количество пар каждого типа, 0, если (xi, uj)ÏГ1 |
|||||||||||||||||||||||||||||||||||
|
Ориентированный гиперграф |
|
– |
|
{n} – множество номеров вершины в гипердуге uj, если (xi, uj)ÎГ1; 0, если (xi, uj)ÏГ1 |
Аналогичные обозначения можно использовать для представления смешанных ультраграфов, в которых ни одна вершина не входит в ультрадугу дважды. Повторное вхождение вершины в ультрадугу при условии, что
![]() Ç
Ç![]() = Æ (1)
= Æ (1)
может быть обозначено коэффициентом кратности k, например, <a, k>. При нарушении условия (1) элемент матрицы инциденций ультраграфа должен быть представлен парой двоек:
 ,
,
где a – признак инцидентности вершины началу ультрадуги, b – признак инцидентности вершины концу ультрадуги, а k1, k 2 – количество вершин, входящих в ультрадугу в каждом качестве.
Представление ориентированного гиперграфа матрицей инциденций должно учитывать порядок вхождения вершин в гипердугу, что можно показать, используя нумерацию. Возможность повторного вхождения вершины в дугу приводит к тому, что элемент матрицы инцидентности должен задаваться множеством номеров:
 ,
,
где n – номер вхождения вершины xi в гипердугу uj, причем |{n}| = |(xi, uj)|.
В таблице 3 представлены способы матричного представления основных структурных моделей.
Таблица 3 – Матричное представление основных структурных моделей
|
Модель |
Элемент матрицы смежности вершин |
Элемент матрицы инцидентности вершина-ребро |
|
Неориентированный граф |
1, если вершины смежны**; 0, если вершины не смежны *** |
1, если вершина и ребро инцидентны; 0, если вершина и ребро не инцидентны |
|
Неориентированный мультиграф |
k – количество звеньев, связывающих смежные вершины; 0 – вершины не смежны |
то же |
|
Ориентированный граф |
1, если вершины смежны; 0, если вершины не смежны |
a, если вершина инцидентна началу дуги; b, если вершина инцидентна концу дуги; 0, если не инцидентны |
|
Ориентированный мультиграф |
k – количество дуг, связывающих смежные вершины; 0, если вершины не смежны |
то же |
|
Смешанный мультиграф |
k – количество ребер (дуг и звеньев или петель), связывающих смежные вершины; 0 – если вершины не связаны |
a, если вершина инцидентна началу дуги; b, если вершина инцидентна концу дуги; с, если вершина инцидентна звену; d, если это петля при вершине; 0, если не инцидентны |
|
Гиперграф и гиперграф с кратными ребрами |
то же без учета различия гиперребер*
|
k – количество вхождений вершины в гиперребро, если вершина инцидентна ребру, 0, если вершина не инцидентна ребру |
|
Ориентированный гиперграф и ориентированный гиперграф с кратными дугами |
то же без учета различия гипердуг и порядка вхождения дуги в гипердугу* |
{n}– множество номеров данной вершины в гипердуге, если вершина инцидентна гипердуге; 0 – если вершина не инцидентна гипердуге |
|
Ультраграф и ультраграф с кратными дугами |
то же без учета различия ультрадуг* |
(<а, k1>,<b, k2>), где a – признак инцидентности началу дуги, b – признак инцидентности концу дуги, а ki – количество вершин каждого типа, если вершина инцидентна дуге; 0, если вершина не инцидентна дуге
|
* – не позволяет адекватно задавать графовую модель;
** – вместо «1» можно указать вес ребра или дуги;
*** – возможно задание также через смежность ребер
Для моделей с незначительным количеством связей использование матричной формы задания отношений нецелесообразно, поскольку матрица получается сильно разреженной. В этом случае используют аналитическое представление [3].
Аналитическое представление графовых моделей. Аналитически графовые модели определяются отображениями соответственно образами по отношению смежности вершин XFX, ребер UFU и по отношению инцидентности вершины-ребра XГU или ребра-вершины UГX. При построении образов отображений по отношению смежности для гиперграфов и ультраграфов необходимо также как при построении матриц смежности перейти от n-местных к двуместным отношениям.
Аналитическое задание через отношение смежности вершин возможно только для графов и мультиграфов (см. таблицу 4), поскольку отношения, характеризующие связи в этих моделях, как уже говорилось выше, двуместны изначально. Для неориентированного графа возможно построение аналитического представление отношения смежности ребер, которое также позволяет задать граф.
Таблица 4 – Аналитическое задание отношений смежности
|
Название модели |
Графическое представление
|
X F X |
U F U |
||
|
i |
~ Fxi |
j |
~ Fuj |
||
|
Неориентированный граф |
|
1 2 3 4 |
{x1, x2, x3} {x1} {x1, x4} {x3} |
0 1 2 3 |
{u0, u1, u2} {u0,u2} {u0, u1, u3} {u2}
|
|
Гиперграф* |
|
1 2 3 4 |
{x1, x2, x3} {x1, x3, x4} {x1, x2, x4} {x2, x3} |
0 1 2 3 |
{u1} {u0, u2, u3} {u1, u3} {u1, u2}
|
|
Смешанный мультиграф |
|
1 2 3 4 |
{x1, x3} {x1} {x1, x4} {x3}
|
– |
|
|
Смешанный ультраграф* |
|
1 2 3 4 |
{x1, x2, x3} {x3} {x4} {x1, x2} |
– |
|
|
Смешанный ультраграф с кратными гипердугами* |
|
1 2 3 4 |
{x1, x3} {x3} {x 4} {x3} |
– |
|
|
Ориентированный гиперграф* |
|
1 2 3 4
|
{x1, x2} {x3} {x4} {x3} |
– |
|
* – не позволяет адекватно задать графовую модель.
Аналитическое задание гиперграфа и ультраграфа возможно только через отношение инцидентности (см. таблицу 5). При этом каждое ребро может соединять более двух вершин, а, следовательно, |Гuj| ³ 2 (соответственно, |![]() | ³ 1, |
| ³ 1, |![]() | ³ 1 – для ультраграфа). Повторное вхождение вершин в гиперребро или ультрадугу отображается повторным вхождением идентификатора вершины в соответствующие образы Fxi, Гuj (соответственно
| ³ 1 – для ультраграфа). Повторное вхождение вершин в гиперребро или ультрадугу отображается повторным вхождением идентификатора вершины в соответствующие образы Fxi, Гuj (соответственно ![]() ,
, ![]() – для ультраграфа), которые при этом становятся мультимножествами.
– для ультраграфа), которые при этом становятся мультимножествами.
Таблица 5 – Аналитическое задание отношений инцидентности
|
Название модели |
Графическое представление |
X Г U |
U Г X |
||||||||
|
i |
® Гxi |
¬ Гxi |
~ Гxi |
o Гxi |
j |
® Гuj |
¬ Гuj |
~ Гuj |
o Гuj |
||
|
Неориентированный граф |
|
1 2 3 4 |
– |
– |
{u1,u2,u0} {u1} {u2, u3} {u3} |
– |
0 1 2 3 |
– |
– |
{x1} {x1, x2} {x1, x3} {x3, x4} |
– |
|
Гиперграф |
|
1 2 3 4 |
– |
– |
{u1, u0} {u1, u3} {u1,u2,u3} {u2, u3} |
– |
0 1 2 3 |
– |
– |
{x1} {x1,x2,x3} {x3, x4} {x2,x3,x4}
|
– |
|
Смешанный мультиграф |
|
1 2 3 4 |
Æ {u1, u5} Æ Æ
|
{u1, u5} Æ Æ Æ |
{u2} Æ {u2, u3} {u3, u4} |
{u0} Æ Æ Æ |
0 1 2 3 4 5 |
Æ {x1} Æ Æ {x1} Æ |
Æ {x2} Æ Æ {x2} Æ |
Æ Æ {x1, x3} {x3, x4} Æ {x3, x4} |
{x1} Æ Æ Æ Æ Æ |
|
Смешанный ультраграф |
|
1 2 3 4 |
{u1} {u1} Æ Æ
|
Æ {u1} {u1} Æ |
Æ Æ {u2} {u2} |
{u0} Æ Æ Æ |
0 1 2 3 |
Æ {x1,x2} Æ {x4} |
Æ {x3} Æ {x1,x3} |
Æ Æ {x3, x4} Æ
|
{x1} Æ Æ Æ
|
|
Смешанный ультраграф с кратными ребрами |
|
1 2 3 4 |
{u1, u3} {u1, u3} Æ Æ |
Æ Æ {u1, u3} Æ |
Æ Æ {u2} {u2} |
{u0} Æ Æ Æ |
0 1 2 3 |
Æ {x3} Æ {x3} |
Æ {x1,x2} Æ {x1,x2} |
Æ Æ {x3, x4} Æ |
{x1} Æ Æ Æ |
|
Ориентированный гиперграф |
|
1 2 3 4
|
Æ Æ Æ Æ |
Æ Æ Æ Æ |
{<u1,1>} {<u1,2>} {<u1,3>, u2} {u2} |
{u0} Æ Æ Æ |
0 1 2
|
Æ Æ Æ |
Æ Æ Æ |
Æ (x1,x2,x3) {x3, x4} |
{x1} Æ Æ |
Аналитическое задание ориентированного гиперграфа требует определения порядка пар в кортеже пар гипердуги, что можно сделать, используя в качестве Гuj кортежи. При использовании отображения ГX этот порядок необходимо показать явно, используя номера: <ur, kr>, где kr – номер вершины в указанном гиперребре.
В таблице 6 рассмотрены способы аналитического представления основных графовых моделей.
Таблица 6 – Способы аналитического описания графовых моделей
|
Модель |
Представление через отношение смежности |
Представление через отношение инцидентности |
Примечание |
|
Неориентированный граф или мультиграф |
G(X, FX),
X = {xi / i =
FX = {Fxi / i = Fxi = Xi Í X |
G(X, U, ГX),
X = {xi / i =
ГX = {Гxi / i = Гxi = Ui Í U |
Для мультиграфа образы Fxi, Fuj могут представлять собой мультимножества |
|
G(U, FU)*,
U = {uj / j =
FU = {Fuj / j = Fuj = Uj Í U |
G(X, U, ГU),
X = {xi / i =
ГU = {Гuj / j = Гuj = Xj Í X, |Гuj | = 2 |
||
|
Гиперграф и гиперграф с кратными ребрами |
то же, но без учета различия гиперребер* |
то же, но |Гuj | ³ 2 |
При повторном входе вершин в ребро uj образы Fxi и Гuj будут мультимножествами |
|
Ориентированный граф (мультиграф)
|
G(X, FX),
X = {xi / i =
FX = {
F̉X = { F̉xi = {xi}},
|
G(X, U, ГX),
X = {xi / i =
ГX = {
|
Для мультиграфа образы
|
|
G(X, U, ГU),
X = {xi / i =
ГU = {
|
|||
|
Ультраграф и ультраграф с кратными дугами |
то же, но без учета различия ультрадуг* |
то же, но | |
При повторном вхождении вершин в дугу uj образы |
|
Ориентированный гиперграф с кратными дугами |
то же, но без учета различия гипердуг и порядка вхождения части дуги в дугу* |
G(X, U, ГX),
X = {xi / i =
ГX = {Гxi / i = Гxi = {<ur,kr>}, ur Î Ui Í U |
kr – номер вершины в гипердуге |
|
G(X, U, ГU),
X = {xi / i =
ГU = {Гuj / j = Гuj = Xj Í X, |Гuj | = 2 |
Гuj – кортеж |
* – не позволяет адекватно задать графовую модель
Представление иерархических моделей. Для реализации стратегий проектирования «снизу-вверх» и «сверху-вниз» представление иерархических моделей помимо отношений смежности и инцидентности должно позволять задавать бинарное отношение вхождения Ri вершин i-1-го уровня в вершину i-го уровня или обратное ему бинарное отношение включения (Ri)-1 вершин i-1-го уровня в вершину i-го уровня.
Отношение вхождения при этом определяется как
{(![]() ,
,![]() )/
)/![]() Î
Î![]() } Ì Ri Ì
} Ì Ri Ì ![]() ´
´ ![]() ,
,
где ![]() ,
, ![]() – вершины i-го и i-1-го уровня соответственно;
– вершины i-го и i-1-го уровня соответственно;
![]() – подмножество вершин i-1-го уровня, соответствующее
– подмножество вершин i-1-го уровня, соответствующее ![]() , т. е. k-ой вершине i-го уровня;
, т. е. k-ой вершине i-го уровня;
![]() ,
,![]() – множества вершин i-го и i-1-го уровня соответственно.
– множества вершин i-го и i-1-го уровня соответственно.
Отношение вхождения представляет собой отношение смежности вершин соседних уровней, и потому его можно задать матрицей смежности или аналитически. При этом, описывая иерархию i = ![]() матрицей смежности, необходимо построить матрицу размерностью (
матрицей смежности, необходимо построить матрицу размерностью (![]() )2 элементов, которая получится сильно разреженной. Учтя то, что по отношению вхождения вершин иерархия является ориентированным деревом, и, следовательно, строки матрицы, соответствующие элементам верхнего q-го уровня, и столбцы, соответствующие элементам нижнего 0-го уровня, содержат нули, размер таблицы можно сократить до
)2 элементов, которая получится сильно разреженной. Учтя то, что по отношению вхождения вершин иерархия является ориентированным деревом, и, следовательно, строки матрицы, соответствующие элементам верхнего q-го уровня, и столбцы, соответствующие элементам нижнего 0-го уровня, содержат нули, размер таблицы можно сократить до ![]() ´
´ ![]() элементов.
элементов.
Аналогично при описании иерархии аналитически можно не указывать образы элементов верхнего уровня. Всего при аналитическом описании иерархии i = ![]() необходимо будет построить
необходимо будет построить ![]() образов по одному элементу в каждом, поскольку каждая вершина i-1- го уровня входит в единственную вершину i-го уровня.
образов по одному элементу в каждом, поскольку каждая вершина i-1- го уровня входит в единственную вершину i-го уровня.
Кроме того, отношение Ri сюръективно, следовательно, его можно задать таблицей соответствия, в которых каждой вершине i-1-го уровня ![]() – аргументу функции сопоставлена вершина i-го уровня
– аргументу функции сопоставлена вершина i-го уровня ![]() – значение функции (см. рисунок 1 и таблицу 7). Количество столбцов такой таблицы равно |
– значение функции (см. рисунок 1 и таблицу 7). Количество столбцов такой таблицы равно |![]() | = ni-1, а количество строк равно 2. Соответственно, для иерархии i =
| = ni-1, а количество строк равно 2. Соответственно, для иерархии i = ![]() необходимо задать q таблиц соответствия, суммарным объемом V1 =
необходимо задать q таблиц соответствия, суммарным объемом V1 = ![]() элементов.
элементов.

Рисунок 1 – Пример иерархической модели
Таблица 7 – Таблица соответствия отношения R1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 8 – Таблица соответствия отношения R2
|
|
|
|
|
|
|
|
|
|
|
|
Отношение включения (Ri)-1 – многозначно, т. е. не является функциональным, следовательно, его нельзя задать таблицей соответствия. Для его определения целесообразно использовать аналитическое представление. При этом для описания отношения включения на i-м уровне необходимо задать |![]() | = ni образов вида:
| = ni образов вида:
(Ri)-1![]() = {
= {![]() /
/![]() Î
Î![]() &
& ![]() Î
Î![]() & (
& (![]() ,
, ![]() ) Î (Ri)-1} =
) Î (Ri)-1} = ![]() .
.
Соответственно, для иерархии i = ![]() необходимо задать q отображений, общим объемом V2 =
необходимо задать q отображений, общим объемом V2 = ![]() элементов. Например, описание отношения включения модели, представленной на рисунке 1, множеством образов имеет вид:
элементов. Например, описание отношения включения модели, представленной на рисунке 1, множеством образов имеет вид:
|
(R1)-1
(R1)-1
(R1)-1
(R1)-1
(R1)-1 |
(R2)-1
(R2)-1
|
В том случае, если для описания уровней иерархической модели использованы два универсума: универсум вершин и универсум ребер, для снижения вычислительной сложности выполнения операций над иерархической моделью целесообразно также задавать отношение соответствия ребер. Это отношение – инъективная функция
(![]() ,
,![]() ) Î
) Î ![]() Ì
Ì ![]() ´
´![]() или (
или (![]() ,
,![]() ) Î (
) Î (![]() )-1 Ì
)-1 Ì![]() ´
´![]() ,
,
где ![]() ,
, ![]() – ребра i-1 и i-го уровней соответственно,
– ребра i-1 и i-го уровней соответственно,
![]() , (
, (![]() )-1 – прямая и обратная функции, причем
)-1 – прямая и обратная функции, причем ![]() – частичная, т. е. определена не на всем множестве
– частичная, т. е. определена не на всем множестве ![]() , а только на множество внешних ребер кусков
, а только на множество внешних ребер кусков ![]() , в то время как функция (
, в то время как функция (![]() )-1 – тотальная.
)-1 – тотальная.
Данные функции также можно задать таблицами соответствия для нахождения ребра i – го уровня по ребру i-1 уровня и для нахождения ребра i-1 уровня по ребру i – го уровня. Отличие между этими таблицами заключается в том, что в таблице ![]() множеству внутренних ребер, для которых не определены соответствующие ребра i-го уровня, будет сопоставлено «Æ».
множеству внутренних ребер, для которых не определены соответствующие ребра i-го уровня, будет сопоставлено «Æ».
Выполненные в настоящей работе анализ и систематизация возможных способов представления графовых моделей, а также предложенные способы задания иерархических моделей обеспечивают разработчику алгоритмов решения задач структурного синтеза возможность выбора способа представления моделей или их комбинации, обеспечивающего эффективное выполнение операций алгоритма.
Литература
1. Бершадский А.М. Применение графов и гиперграфов для автоматизации конструкторского проектирования РЭА и ЭВА. – Саратов: Изд-во Саратовского ун-та, 1983.
2. Мелихов А.Н. Ориентированные графы и конечные автоматы. – М.: Гл. ред. ф.-м. лит. изд «Наука», 1971.
3. Овчинников В.А. Автоматизация комбинаторно-оптимизационных задач при проектировании ЭВМ и систем: Учеб. для вузов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2001.
4. Иванов Б.Н. Дискретная математика. Алгоритмы и программы: Учеб. пособие. – М.: Лаборатория Базовых Знаний, 2002.
Публикации с ключевыми словами: математические модели, оптимизация, структурные модели
Публикации со словами: математические модели, оптимизация, структурные модели
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



















