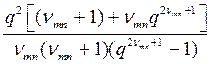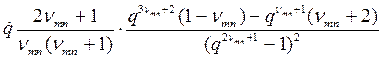научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2013
DOI: 10.7463/1113.0623923
УДК 621.3
Россия, МГТУ им. Н.Э. Баумана
Введение.
Исследованию задач о колебаниях жидкости в баках ракет-носителей посвящено много работ [1-11]. В предыдущих работах авторов [12, 13] приведена постановка модельной задачи о малых движениях несжимаемой жидкости, вытекающей из топливного бака с заборными устройствами (ЗУ). Исследование рассматриваемой задачи в этих работах, проведенные методами функционального анализа и спектральной теории операторных пучков, показало, что спектр нормальных движений несжимаемой жидкости (движений, подчиняющихся закону е-λt) обладает двумя ветвями собственных значений: дискретным множеством вещественных чисел, расположенных на положительной части вещественной оси и дискретным множеством комплексно сопряженных чисел, расположенных вблизи мнимой оси. Действительным собственным значениям отвечают апериодические режимы движения жидкости, происходящие преимущественно вблизи дна топливного отсека, а комплексно сопряженным числам отвечает режимы затухающих колебаний, преобладающих в основном на свободной поверхности жидкости.
В предлагаемой статье приведены примеры рассматриваемых задач о движении несжимаемой жидкости, вытекающей из наиболее распространенных на практике топливных отсеков в виде цилиндра и конуса.
1. Постановка задачи.
Пусть несжимаемая жидкость, частично заполняющая неподвижный бак произвольной формы вытекает через ЗУ и может совершать малые движения. Рассматриваемая проблема малых движений жидкости может быть описана уравнениями гидродинамики, линеаризованными вблизи невозмущённого состояния. Подробная постановка задачи приведена в работах [12-14].
Предполагая возмущенное движение жидкости потенциальным, сформулируем краевую задачу о колебаниях вытекающей жидкости для потенциала скоростей ![]() в виде
в виде
![]() в области, заполненной жидкостью,
в области, заполненной жидкостью, ![]() ,
,
 на смачиваемой поверхности
на смачиваемой поверхности![]() ,
,
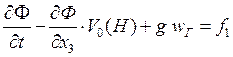 на свободной поверхности Г0, (1)
на свободной поверхности Г0, (1)
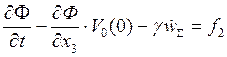 на поверхности слива
на поверхности слива![]() ,
,
![]() (
( ![]() .
. ![]() .
. ![]() .0 ) =
.0 ) = ![]() , при
, при ![]() ,
,
где ![]() - производная по внешней нормали к поверхности
- производная по внешней нормали к поверхности ![]() ;
; 
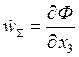 - малые смещения и скорость частиц жидкости на поверхностях Г0 и
- малые смещения и скорость частиц жидкости на поверхностях Г0 и ![]() соответственно,
соответственно, ![]() - обобщенный коэффициент сопротивления поверхности слива,
- обобщенный коэффициент сопротивления поверхности слива, ![]() коэффициент гидравлического сопротивления поверхности слива,
коэффициент гидравлического сопротивления поверхности слива, ![]() - величина интенсивности внешнего однородного поля массовых сил,
- величина интенсивности внешнего однородного поля массовых сил, ![]()
![]() - заданные поля внешних воздействий соответственно на поверхностях Г0 и
- заданные поля внешних воздействий соответственно на поверхностях Г0 и ![]() .
.
Проинтегрировав уравнение неразрывности по объёму, занимаемому жидкостью, для любого момента времени t, получим дополнительное интегральное условие ![]() которому должны подчиняться поле скоростей и поле смещений в рассматриваемой задаче.
которому должны подчиняться поле скоростей и поле смещений в рассматриваемой задаче.
Впервые исследование колебаний жидкости с учетом вытекания было предложено Кирилловым В.В. [15] и продолжено в работах [5], [11], [16]. В упомянутых работах рассматривались задачи для жидкости, занимающей часть цилиндрического бака, на дне которого ставилось кинематическое условие вытекания.
2. Колебания жидкого топлива в цилиндрической ёмкости
Рассмотрим задачу о собственных движениях жидкости, вытекающей через заборное устройство из цилиндрической ёмкости при наличии свободной поверхности. Используя цилиндрические координаты r, ![]() ,
, ![]() с началом на поверхности слива, получим задачу для определения потенциала скоростей
с началом на поверхности слива, получим задачу для определения потенциала скоростей ![]() :
:
 ,
, ![]() ,
,
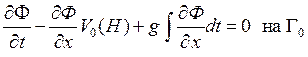 , (2)
, (2)
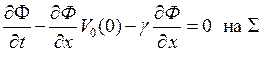 ,
,
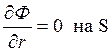 ,
,
![]() =
= ![]() при
при ![]() .
.
Функцию ![]() представим в виде суммы двух функций
представим в виде суммы двух функций
![]() ,
,
и будем искать каждый потенциал ![]() и
и ![]() в виде
в виде
произведения четырёх функций:
![]()
![]()
где ![]() - функция периода
- функция периода ![]() , функция
, функция ![]() удовлетворяют уравнению Бесселя, а функции
удовлетворяют уравнению Бесселя, а функции ![]() ,
, ![]() есть решения задач
есть решения задач
 (3)
(3)
 (4)
(4)
Используя метод разделения переменных, находим выражения для потенциалов скоростей
 , (5)
, (5)
 , (6)
, (6)
где ![]() - функция Бесселя 1-го рода, m-го порядка,
- функция Бесселя 1-го рода, m-го порядка, ![]() - корни уравнения
- корни уравнения ![]() , а функции
, а функции ![]() удовлетворяют системе уравнений
удовлетворяют системе уравнений
 (7)
(7)
где ![]() ,
,![]() - коэффициенты инерционных и диссипативных связей,
- коэффициенты инерционных и диссипативных связей, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - динамические характеристики парциальных подсистем
- динамические характеристики парциальных подсистем

Для определения собственных частот рассматриваемой механической системы, положим ![]() Из уравнений (7) получаем характеристической уравнение
Из уравнений (7) получаем характеристической уравнение
![]() . (8)
. (8)
Здесь ![]() - комплексный коэффициент затухания волновых движений жидкости
- комплексный коэффициент затухания волновых движений жидкости ![]() .
.
Уравнение (8) имеет две ветви решений: действительные корни и ветвь комплексно сопряженных корней. Для исследования уравнения введём безразмерные параметры
![]()
и перепишем уравнение (8) в безразмерном виде
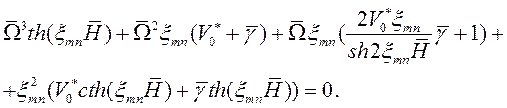 (9)
(9)
Результаты вычислений корней кубического уравнения (9) приведены в таблице (1).
В случае глубокой жидкости ![]()
уравнение (19) принимает вид
![]()
и имеет корни
![]() (10)
(10)
В таблице № 1 представлены результаты вычислений безразмерных собственных частот и коэффициентов распределения ![]() при
при ![]() , m=1, n=1,
, m=1, n=1,![]() для различных значений
для различных значений ![]() ,
, ![]() , а на рис. 1-4 показаны формы колебаний.
, а на рис. 1-4 показаны формы колебаний.
Таблица № 1 - Собственные частоты колебаний жидкости в цилиндрической емкости при перераспределении жидкости из бака
|
|
|
|
|
|
0 | 0,05 | -12,348 | -0,00742±1,324i | -0,306 | -0,00408±0,036i |
0 | 0,15 | -4,080 | -0,021±1,330i | -0,280 | -0,0338±0,0990i |
0,04 | 0,01 | -61,834 | -0,00268±1,32318i | -0,309 | -0,0003±0,0073i |
0,04 | 0,05 | -12,37 | -0,00857±1,32413i | -0,305 | -0,0047±0,0360i |
0,04 | 0,1 | -6,175 | -0,01544±1,3266i | -0,295 | -0,0170±0,0690i |
0,04 | 0,15 | -4,103 | -0,02143±1,330i | -0,279 | -0,0340±0,0980i |
0,07 | 0,01 | -61,85 | -0,00357±1,32322i | -0,309 | -0,0004±0,0073i |
0,07 | 0,05 | -12,387 | -0,00942±1,32432i | -0,305 | -0,0052±0,0360i |
0,07 | 0,1 | -6,192 | -0,0162±1,326946i | -0,294 | -0,0178±0,0690i |
0,07 | 0,15 | -4,12 | -0,022±1,3307167i | -0,278 | -0,036±0,097i |
0,1 | 0 | -6,181e-9 | -0,003±1,323i | -0,309 | -3,26e(-12) ±7,33e(-11)i |
0,1 | 0,01 | -61,867 | -0,00445±1,3232i | -0,309 | -0,0005±0,0073i |
0,1 | 0,05 | -12,404 | -0,0103±1,3245i | -0,305 | -0,0056±0,036i |
0,1 | 0,1 | -6,209 | -0,0169±1,3272i | -0,293 | -0,019±0,069i |
0,1 | 0,15 | -4,137 | -0,0227±1,3311i | -0,276 | -0,037±0,096i |

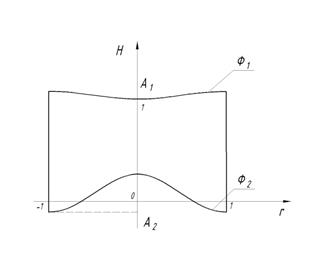
Н=0.5 Н =1
Рис. 1. Формы колебаний жидкости в цилиндрическом сосуде при
Ω*=-61.834, , m=0, n=1, ![]() =3. 83, А1/А2=-0.309.
=3. 83, А1/А2=-0.309.


Н=0.5 Н=1
Рис. 2. Формы колебаний жидкости в цилиндрическом сосуде при различных Н при Ω*=-0.0027+1.32i, m=1, n=1, ![]() =1.841, А2/А1=0.007.
=1.841, А2/А1=0.007.


Н=0.5 Н=1
Рис. 3. Формы колебаний жидкости в цилиндрическом сосуде при различных Н при Ω*=-122.45, m=1, n=1, ![]() =1.841, А1/А2=-0.043.
=1.841, А1/А2=-0.043.
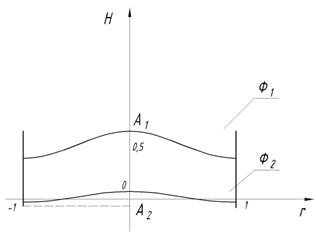

Н=0.5 Н=1
Рис. 4. Формы колебаний жидкости в цилиндрическом сосуде при различных Н при Ω*=-0.000076+1.96i, m=0, n=1, ![]() =3. 83, А2/А1=0.0007.
=3. 83, А2/А1=0.0007.
3. Колебания жидкого топлива в конической ёмкости
Рассмотрим круговой конус, частично заполненный жидкостью. Введем сферическую систему координат ![]() с центром в вершине конуса (рис. 5). Угол
с центром в вершине конуса (рис. 5). Угол ![]() отсчитывается от положительного направления оси OZ, угол
отсчитывается от положительного направления оси OZ, угол ![]() измеряется в плоскости OXY от оси OX, сторону оси OY . Из рис. 5 следует. что
измеряется в плоскости OXY от оси OX, сторону оси OY . Из рис. 5 следует. что ![]() ,
, ![]() ,
, ![]() . Если ограничиться малым углом конусности. то оказывается правомерным граничное условие для плоской невозмущённой свободной поверхности рассматривать на части сферической поверхности R=R1. Очевидно, что уравнение для конической полости R=R2, боковой поверхности -
. Если ограничиться малым углом конусности. то оказывается правомерным граничное условие для плоской невозмущённой свободной поверхности рассматривать на части сферической поверхности R=R1. Очевидно, что уравнение для конической полости R=R2, боковой поверхности - ![]() . Условием применимости полученных формул для плоской свободной поверхности является следующее ограничение, накладываемое на угол конусности:
. Условием применимости полученных формул для плоской свободной поверхности является следующее ограничение, накладываемое на угол конусности: ![]() . Наиболее полное исследование колебаний жидкости в усечённых конических баках без учёта эффекта вытекания приведено в работе [18].
. Наиболее полное исследование колебаний жидкости в усечённых конических баках без учёта эффекта вытекания приведено в работе [18].

Рис. 5. Геометрические характеристики обратного и прямого конусов
Примем за характерный размер радиус дна конической полости R=R2 и введем безразмерный радиус r = R/R2. Обозначим q = R1/R2. Допустим далее, что жидкость либо достигает вершины конуса, либо конус усеченный и имеет дно R=R2 (рис. 5 а, б). Для сокращения будем называть полость на рис. 5 а - обратным усеченным (не усеченным) конусом (q > 1).
Краевая задача о свободных колебаниях жидкости в конической полости имеет вид
![]() .
.  ,
,
 ,
,
 , (11)
, (11)
где ![]() - лапласиан, записываемый в сферических координатах [17].
- лапласиан, записываемый в сферических координатах [17].
Потенциал скоростей ![]() для конической полости представим в виде суммы потенциалов
для конической полости представим в виде суммы потенциалов
![]() , (12)
, (12)
каждый из которых есть произведение функций
![]() ,
, ![]() ,
,
где ![]() -присоединённая функция Лежандра, а функции
-присоединённая функция Лежандра, а функции ![]() , есть решения краевых задач
, есть решения краевых задач
 (13)
(13)
 (14)
(14)
Используя метод разделения переменных, находим представления решений поставленных краевых задач
 , (15)
, (15)
 ,
,
где 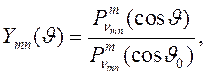 - присоединенные функции Лежандра первого рода,
- присоединенные функции Лежандра первого рода, ![]() -го порядка,
-го порядка, ![]() - n –ый корень уравнения
- n –ый корень уравнения
 .
.
Функции ![]() .
. ![]() соответственно равны
соответственно равны
 , (16)
, (16)
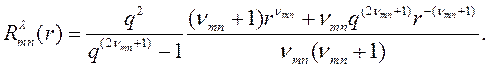
Подставив полученные решения (16) в граничные условия (11), и предполагая, что ![]() , получим уравнение для определения собственных чисел:
, получим уравнение для определения собственных чисел:
![]() (17)
(17)
где коэффициенты вычисляются по формулам
 (18)
(18)
Коэффициенты инерционных и диссипативных связей и квадрат парциальной частоты ![]() колебаний свободной поверхности жидкости в коническом баке представлены в таблице 2.
колебаний свободной поверхности жидкости в коническом баке представлены в таблице 2.
Таблица № 2 – Коэффициенты ![]() при обобщенных координатах для вычисления
при обобщенных координатах для вычисления ![]() при
при ![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В таблице 3 представлены результаты расчетов собственных чисел в зависимости от скорости ![]() и параметра
и параметра ![]() .
.
Таблица № 3 - Собственные частоты колебаний жидкости в конической емкости при ![]() ,
,![]() , m=1, n=1.
, m=1, n=1.
|
|
|
|
0 | 0 | 0 | 0,000± 0,974i |
0 | 0,2 | -15,798 | -0,004 ± 0,974i |
0,05 | 0,2 | -15,704 | -0,008 ± 0,975i |
0,1 | 0,2 | -15,610 | -0,012 ± 0,975i |
0 | 0,5 | -6,302 | -0,010 ±0,976i |
0,05 | 0,5 | -6,208 | -0,014 ± 0,976i |
0,1 | 0,5 | -6,114 | -0,018 ± 0,977i |
0 | 1 | -3,123 | -0,019±0,980i |
0,05 | 1 | -3,028 | -0,023 ± 0,981i |
0,1 | 1 | -2,934 | -0,027 ± 0,982i |
Также рассматриваемая модельная задача для конической области была решена вариантом метода конечных элементов (МКЭ), численно реализующим нахождение обобщённого решения некоторого интегрального тождества, полученного методом Галёркина. В следующих таблицах приведены результаты расчетов для конусов, аналогично изображенных на рисунке 5, но с плоским дном (таблица № 4) и с плоской свободной поверхностью (таблица № 5).
Таблица № 4 - Собственные частоты колебаний жидкости в конической емкости с плоским дном при ![]() ,
,![]() , m=1, n=1.
, m=1, n=1.
|
|
|
|
0 | 0 | 0 | 0,00± 0,9909i |
0 | 0,2 | -17,569 | -0,001861 ± 0,9909i |
0 | 0,5 | -7,02015 | -0,004585 ± 0,99142i |
0 | 1 | -3,4977 | -0,008707 ± 0,99316i |
Таблица № 5 - Собственные частоты колебаний жидкости в конической емкости с плоской свободной поверхностью при ![]() ,
,![]() , m=1, n=1.
, m=1, n=1.
|
|
|
|
0 | 0 | 0 | 0,00±2,5746i |
0 | 0,2 | -10,47867 | -0,01931 ±2,57469i |
0 | 0,5 | -4,11859 | -0,03727 ±2,59303i |
0 | 1 | -2,011915 | -0,0401 ± 2,62067i |
В заключение необходимо отметить, что полученные результаты подтверждают выводы, сформулированные ранее в работах авторов [12, 13], то есть спектр нормальных движений несжимаемой жидкости, вытекающей из ограниченной области, обладает двумя ветвями собственных значений: дискретного множества вещественных чисел, и дискретного множества комплексно-сопряженных чисел, расположенных вблизи мнимой оси.
Список литературы
1. Колесников К.С. Динамика ракет. М.: Машиностроение, 2003. 500 с.
2. Луковский И.А. Введение в нелинейную динамику твердого тела. Киев: Наукова думка, 1990. 296 с.
3. Рабинович Б.И. Введение в динамику ракет-носителей космических аппаратов. М.: Машиностроение, 1975. 416 с.
4. Микишев Г.Н.. Рабинович Б.И. Динамика тонкостенных конструкций с отсеками, содержащими жидкость. М.: Машиностроение, 1971. 563 с.
5. Моисеев Н.Н., Петров А.А. Численные методы расчёта собственных частот колебаний ограниченного объёма жидкости. М.: ВЦ АН СССР, 1966. 270 с.
6. Моисеев Н.Н. Румянцев В.В. Динамика тел с полостями, содержащими жидкость. М.: Наука, 1965. 440 с.
7. Черноусько Ф.Л. Движение твердого тела с полостями, содержащими вязкую жидкость. М.: ВЦ АН СССР, 1968. 232 с.
8. Фещенко С.Ф., Луковский И.А., Рабинович Б.И., Докучаев Л.В. Методы определения присоединенных масс жидкости в подвижных полостях. Киев: Наукова думка, 1969. 250 с.
9. Нариманов Г.С., Докучаев Л.В., Луковский И.А. Нелинейная динамика летательного аппарата с жидкостью. М.: Машиностроение, 1977. 203 с.
10. Колесников К.С., Шкапов П.М., Пожалостин А.А. Задачи динамики гидромеханических систем в трудах кафедры теоретической механики имени профессора Н.Е. Жуковского // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2012. Спец. вып. № 8. С. 15-30.
11. Лимарченко О.С., Матараццо Д., Ясинский В.В. Динамика вращающихся конструкций с жидкостью. Киев: ГНОЗИС, 2002. 304 с.
12. Степанова М.И., Темнов А.Н. Малые движения жидкости с поверхностной диссипацией энергии // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2011. № 4. С. 99-110.
13. Дьяченко М.И., Темнов А.Н. Собственные колебания жидкого топлива в условиях перераспределения // Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2012. № 3. С. 31-38.
14. Дьяченко М.И., Темнов А.Н. Проблемы динамики перераспределения топлива в крупногабаритных ракетно-космических объектах // Вестник МГТУ им. Н.Э. Баумана. Сер. Машиностроение. 2012. Спец. вып.С. 164-174.
15. Кириллов В.В. Исследование колебаний жидкости в неподвижном сосуде с учётом её вытекания // Труды МФТИ. 1960. Вып. 5. С. 19-25.
16. Орлов В.В., Темнов А.Н. Малые движения жидкости, вытекающей из бака // Современные методы теории функций и смежные проблемы : тез. докладов. Воронеж: Изд-во ВГУ, 1997. С. 124.
17. Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Основные дифференциальные уравнения математикой физики. М.: Физматлит, 1962. 767 с.
18. Луковский И.А., Солодун А.В., Тимоха А.Н. Собственные колебания жидкости в усеченных конических баках // Акустический вестник. 2006. Т. 9, № 3. С. 42-61.
Публикации с ключевыми словами: цилиндрический и конический бак, перераспределение, пакетная схема, собственный числа и собственные формы колебания
Публикации со словами: цилиндрический и конический бак, перераспределение, пакетная схема, собственный числа и собственные формы колебания
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||