научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2013
DOI: 10.7463/1113.0623507
УДК 621.923
Россия, МГТУ им. Н.Э. Баумана
Введение
Абразивно-экструзионная обработка (АЭО) – относительно новый вид абразивной обработки. Первое упоминание о ней появилось около полувека назад. Суть процесса заключается в продавливании (экструзии) абразивной пасты вдоль обрабатываемых поверхностей (в большинстве случаев сквозных отверстий) и съема материала абразивными частицами, содержащимися в пасте. Применяемые при обработке абразивные пасты состоят из абразивных зерен и связующего вещества, представляющего собой вязко-упругую жидкость, основным компонентом которой является высокомолекулярные полимерные соединения.
В современной гидродинамике достаточно хорошо изучена теория движения жидкостей в самых различных условиях [1, 2, 3]. В том числе достаточно развита теория движения вязких жидкостей [4, 5]. Практически отсутствуют работы по движению вязко-упругих жидкостей. Дело в том, что ни в каких иных областях техники, кроме АЭО, подобные процессы не применяются. Публикации носят, в-основном, описательный, рекламный характер. АЭО базируется на чисто эмпирических подходах в разработке технологических процессов. Ввиду новизны этого способа обработки и весьма узкими областями ее промышленного применения вопросам теории практически не уделяется внимания. В то же время не подлежит никакому сомнению, что изучение закономерностей процессов, происходящих при АЭО, выявление зависимостей процесса от влияющих факторов, позволит существенно повысить эффективность технологии и расширить сферы ее практического применения. Целью работы является рассмотрение концепции создания математической модели происходящих физических процессов при АЭО ввиду отсутствия в публикациях результатов исследований, которые можно было бы принять при расчете характеристик АЭО.
Аналитическая часть
Одной из основных задач исследования изучаемого процесса является определение закона движения абразивных частиц в потоке абразивной пасты. Именно траектории абразивных частиц и их воздействие на частицы, находящиеся в контакте с обрабатываемой поверхностью, создает условия, достаточные для начала процесса микрорезания этими пограничными абразивными зернами.
Таким образом, предстоит применить законы гидродинамики к потоку суспензии, твердым составляющим которой являются абразивные зерна определенного размера в высокой концентрации, а жидкой составляющей – вязко-упругая жидкость.
Основной гипотезой при описании изучаемого процесса примем гипотезу сплошности, состоящую в том, что все макроскопические физические, химические и термодинамические параметры являются конечными и непрерывными функциями пространственных координат в любом бесконечно малом объеме несущей среды. При этом под бесконечно малым объемом среды понимается объем, малый по сравнению с характерным объемом, занимаемым средой, но бесконечно большой по сравнению с объемом молекул, из которых состоит среда.
В классической гидродинамике в основном рассматриваются однородные жидкости и газы, подчиняющиеся простым уравнениям состояния (модель совершенного газа, баротропные процессы), хотя любые реальные жидкости и газы подчиняются уравнениям состояния более сложного вида. Изучаемая среда может быть одно- или многокомпонентной. В нашем случае среда – суспензия, включающая в свой состав большое количество абразивных зерен, которые нельзя рассматривать как компонент. В большинстве случаев такую среду рассматривают тоже как сплошную среду с характеристиками, отличными от характеристик несущей среды, которую называют непрерывной или сплошной фазой. Во многих задачах предполагается, что объемная концентрация частиц мала, т.е. дисперсная фаза принимается бесконечно разбавленной. В случае абразивной пасты для абразивно-экструзионной обработки такое допущение неприемлемо, так как эксперименты по использованию паст с объемной концентрацией абразива в 10, 20, 30, 40 процентов показывают, что такой концентрации недостаточно даже для единичного взаимодействия зерна с обрабатываемой поверхностью. То есть, при таких концентрациях обработка не происходит независимо от времени обработки. Поэтому напрямую использовать результаты решения задач гидродинамики суспензий с малой объемной концентрацией частиц в нашем случае неприемлемо. Наиболее близкой задачей, решаемой в прикладных областях гидродинамики, является, ввиду экономической важности, изучение песчаных суспензий с размерами частиц до 100 мкм в области нефте-газо-добычи, концентрация которых не превышает нескольких процентов. Кроме того, такого рода суспензии имеют несущую составляющую на основе воды или углеводородов. Естественно, применять результаты исследований таких процессов неприемлемо для АЭО.
Немаловажную роль играет форма абразивных частиц в пасте. Форма абразивных частиц, применяемых в абразивной обработке, достаточно сложная, поэтому необходимо решать и проблему моделирования их формы при решении задач о движении и взаимодействии их в пасте. В основном, частицы рассматриваются как образования, имеющие регулярную геометрическую форму (сферу, эллипсоиды, диски, цилиндры). В данной работе применяются абразивные пасты на основе электрокорунда белого, частицы которого при явно выраженной кристаллической структуре имеют довольно близкую к сферической форму. Поэтому в первом приближении будем считать форму абразивных зерен в абразивной пасте сферической.
Еще одно предположение, которое будем использовать, это предположение о монодисперсности, т.е. предположение об одинаковых форме и размерах всех абразивных частиц. В действительности абразив, применяемый в промышленности, является полидисперсным, и составляющие его частицы характеризуются непрерывным распределением по размерам. В этом случае следовало бы основными параметрами при рассмотрении параметров частиц пользоваться среднестатистическими характеристиками.
В качестве определяющих уравнений (феноменологических соотношений) в изучении поведения сплошной среды принимают уравнения, следующие из законов сохранения массы, заряда, количества движения, момента количества движения и энергии. Эти уравнения должны быть дополнены соотношениями, отражающими принятую модель сплошной среды. Раздел гидродинамики, изучающий движение жидкости, содержащей макромолекулы и частицы небольших размеров, получили название микрогидродинамики. Из отличительных особенностей микрогидродинамики в общем понимании этого термина к нашему случаю движения абразивной пасты с высокой объемной концентрацией абразивных зерен применимы следующие особенности:
1) Силы инерции, как правило, малы по сравнению с вязкими;
2) Скорость осаждения частиц в жидкости в поле силы тяжести мала, так что частицы можно считать свободно взвешенными в жидкости. Объемная концентрация частиц в жидкости влияет на реологические свойства жидкости;
3) Несущественно броуновское движение частиц в жидкости;
4) Силы поверхностного натяжения играют большую роль, поскольку поверхностные силы пропорциональны площади поверхности частиц, т.е. квадрату их линейного размера, в то время как объемные силы пропорциональны кубу линейного размера;
5) Несущественны электрокинетические явления, так как на процессы резания абразивных зерен эти явления существенного влияния не оказывают, даже при наличии объемного или поверхностного заряда абразивной частицы.
В микрогидродинамике абразивная частица рассматривается как тело, перемещающееся в потоке вязкой жидкости. Выражение для силы, действующей на тело произвольной формы, движущееся поступательно со скоростью U будет выглядеть следующим образом [4]
![]() (1)
(1)
Где Rij – трансляционный или тензор сопротивления; ![]() - динамическая вязкость жидкости; fij – тензор трения.
- динамическая вязкость жидкости; fij – тензор трения.
Элементы, обратные элементам тензора трения 1/fij составляют тензор неподвижности.
Выражение (1) иногда записывается в виде
![]() (2)
(2)
Где Vij – тензор подвижности.
Понятие подвижности является обобщенным понятием, поскольку она характеризует способность к движению частицы под действием любых сил (электрических, магнитных, гравитационных, центробежных и т.д.). Поэтому тензор с компонентами Vij получили название тензор подвижности.
Если тело представляет собой жидкую частицу радиуса a с внутренней вязкостью ![]() , погруженную в жидкость другой вязкости
, погруженную в жидкость другой вязкости ![]() , то выражение для трансляционного вектора принимает вид
, то выражение для трансляционного вектора принимает вид
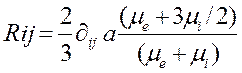 . (3)
. (3)
При ![]() выражение примет вид
выражение примет вид
![]() (4)
(4)
Такое соотношение характерно при движении пузырька в жидкости.
Для твердой частицы (абразивного зерна) характерно обратное соотношение ![]() . Тогда выражение (3) примет вид
. Тогда выражение (3) примет вид
![]() (5)
(5)
В реальности, однако, форма абразивных зерен далека от сферической, и каждое абразивное зерно правильнее рассматривать как эллипсоид. Пусть а1, а2, а3 – полуоси эллипсоида, а R1, R2, R3 – компоненты трансляционного тензора в направлении этих полуосей. В частном случае при а1 = а1а2 = а3 = b эти компоненты определяются выражениями
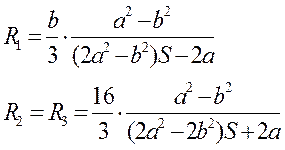 , (6)
, (6)
где параметр S определяется для вытянутого эллипсоида (a>b) выражением
 (7)
(7)
а для сплюснутого эллипсоида (a<b)-выражением
 . (8)
. (8)
При a = b из формулы (5) получается выражение R для сферы.
Движение частицы в потоке жидкости носит случайный характер. Случайной является и ориентация частицы. Для такого движения вводят понятия средних коэффициентов сопротивления, трения и подвижности:
 , (9)
, (9)
Здесь индексами 1, 2, 3 обозначены главные оси квадратичной формы, которой описывается поверхность частицы.
Еще одним важным параметром при движении является момент частицы, вращающейся относительно центра с угловой скоростью ![]() :
:
![]() (10)
(10)
Здесь ![]() –компоненты угловой скорости относительно координатных осей,
–компоненты угловой скорости относительно координатных осей, ![]() – компоненты ротационного вектора.
– компоненты ротационного вектора.
Размерность ![]() равна кубу длины, поэтому тензор интерпретируется как эквивалентный объем.
равна кубу длины, поэтому тензор интерпретируется как эквивалентный объем.
Если частица имеет форму сферы радиуса а, то
![]() (11)
(11)
Для эллипсоида вращения справедливы формулы, аналогичные (6):
 , (12)
, (12)
Для движения абразивной пасты особое значение имеет взаимодействие с другими частицами, поскольку без силового влияния соседних частиц (зерен) не будет происходить процесс резания зерном, находящимся в контакте с обрабатываемой поверхностью заготовки. Другими словами необходимо оценить влияние окружающих частиц (абразивных зерен) на движение рассматриваемой частицы (рабочего абразивного зерна). Воспользуемся выражением для скорости u в точке rжидкости за счет силы F, приложенной в начале координат
 . (13)
. (13)
В случае движения абразивной пасты, а, следовательно наличия частиц отличной от жидкости фазы, изменяются реологические свойства смеси. Если рассматривается движение пробной частицы в такой дисперсной среде, то, оказывается, что это движение аналогично движению в вязкой жидкости, но с эффективным коэффициентом вязкости ![]() , зависящим от объемной концентрации частиц
, зависящим от объемной концентрации частиц ![]() .
.
Для абразивной экструзии особый интерес представляет гидродинамическое влияние на движущееся в вязкой жидкости абразивное зерно других зерен, движущихся в жидкости. При малом объемном содержании абразивных зерен (твердых частиц) частицы находятся относительно далеко и они слабо влияют друг на друга. В первом приближении можно считать, что они движутся независимо, а, следовательно, приведенные выше выражения для скоростей и сопротивлений частиц справедливы. При сближении частиц до расстояний порядка их линейного размера (сто получается при увеличении концентрации) гидродинамическое влияние частиц друг на друга становится существенным и им пренебрегать уже нельзя.
Степень гидродинамического взаимодействия частиц будет зависеть от следующих факторов:
1) форма и размер частиц;
2) расстояния между частицами;
3) ориентация частиц относительно друг друга;
4) ориентация частиц относительно силы тяжести;
5) скорости поступательного и вращательного движения частиц;
6) положение частиц относительно границ области (стенок, межфазной поверхности).
В случае АЭО стенкой будет являться и сама обрабатываемая поверхность.
Большой интерес представляет влияние вышеперечисленных факторов на гидродинамические силы и моменты, действующие на частицы со стороны жидкости. Если эти силы и моменты для определенной совокупности частиц рассчитать, то можно решить обратную задачу определения картины движения частиц по известным массовым силам и моментам.
Если решать задачу классическими методами, то такая модель сводится к линейным уравнениям Стокса, показывающих, что если на частицу действует внешняя сила F, направленная параллельно оси трубы, в которой перемещается абразивная паста, то скорость частицы параллельна оси трубы, т.е. частица не перемещается в радиальном направлении. Это еще раз подтверждает тот факт, что использование в процессе только вязких жидкостей не дает никакого результата независимо от значения вязкости и концентрации абразива. Необходимым свойством связующей жидкости является упругость. Шарик из такой жидкости легко отскакивает при падении на твердое основание.
Экспериментальные исследования движения твердых частиц в трубе постоянного сечения при АЭО показывают [6], что частицы, взвешенные в потоке жидкости, движутся не только в осевом, но и в радиальном направлении. Частицы, плотность которых больше плотности жидкости, мигрируют в радиальном направлении к стенке трубы. Таким образом, для создания модели движения абразивного зерна при АЭО необходимо в выражения (1), (2), (3) и (13) ввести характеристики упругих свойств связующей жидкости, которые существенно повлияют на элементы модели F, Rij, Uj.
Заключение
Рассмотривая движение частиц при АЭО, можно сделать вывод о том, что в потоке жидкости, не обладающей вязко – упругими свойствами и малой концентрации абразивных частиц отсутствует силовое взаимодействие частицы с поверхностью, образующей канал сечения пасты, а, следовательно, и съем материала с этой поверхности. Создание математической модели движения абразивного зерна при АЭО позволит рассчитывать интенсивность изнашивания материала при различных сочетаниях всех факторов, а, значит, прогнозировать основные характеристики технологического процесса, а также качество обработки .
Список литературы
1. Киселев П.Г. Гидравлика: Основы механики жидкости. М.: Энергия, 1980. 360 с.
2. Ладыженская О.А. Математические вопросы динамики вязкой несжимаемой жидкости. М.: Наука, 1970.288 с.
3. Селиванов В.В., Зарубин В.С., Ионов В.Н. Аналитические методы механики сплошной среды. М.: МГТУ им. Н.Э. Баумана, 1994. 384 с.
4. Дой М., Эдвардс С. Динамическая теория полимеров: пер. с англ. М.: Мир, 1998. 440 с.
5. Синайский Э.Г. Гидродинамика физико-химических процессов. М.: Недра, 1997. 339 с.
6. Назаров Н.Г. Абразивно-экструзионная обработка деталей // Наука – производству. 1999. № 10 (23). С. 29-31.
Публикации с ключевыми словами: абразивные зерна, упругость, вязкость, абразивная экструзия
Публикации со словами: абразивные зерна, упругость, вязкость, абразивная экструзия
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



