научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2013
DOI: 10.7463/1013.0622946
УДК 004.942
Россия, МГТУ им. Н.Э. Баумана
Введение
Одной из важнейших задач технологической подготовки машиностроительного производства является проектирование рациональной последовательности сборки изделия. Постановка этой задачи очень проста. Имеется некоторая техническая система (машина или механический прибор), устройство которой задано в комплекте конструкторской документации. Требуется разработать последовательность сборки, минимизирующую затраты на ее реализацию в выбранной производственной и технологической системах. Несмотря на несомненную актуальность данной проблемы и усилия многих отечественных и зарубежных специалистов [2, 9, 16-18], до сих пор не удалось получить эффективного решения, подходящего для большинства классов технических систем и типовых проектных ситуаций.
Последовательность сборки изделия можно считать конструктивно реализуемой, если для каждой устанавливаемой детали выполняются условия базирования и ограничения, накладываемые геометрической разрешимостью. Под базированием понимается взаимная координация деталей, которая достигается фиксацией положения устанавливаемой детали относительно собранного фрагмента изделия. Элементы этой системы координат обычно реализуются в виде участков поверхностей, контактных точек, осей симметрии, искусственной разметки и пр. и называются конструкторскими базами. Геометрической разрешимостью (геометрическим доступом) называется ситуация, когда собранная конфигурация не содержит геометрических препятствий, делающих невозможным установку детали в выбранное положение. В данной работе ограничимся обсуждением условий базирования и способов формализации этой важнейшей структурной и конструктивной характеристики изделий.
Формализация отношения базирования
В технических системах (машинах, приборах, установках и др.) базирование достигается реализацией механических связей (соединений и сопряжений), которые закладываются на стадии конструирования и доставляют изделию механическую связность, а также функциональную и геометрическую определенность. В работах по автоматизации проектирования были предложены многочисленные структурные модели, предназначенные для описания механических связей изделия [1-7, 16, 17, 20]. Если отвлечься от различий в наименованиях и технике генерации моделей, то большинство из них представляют собой парафраз графа механических связей. Этот носитель проектной информации задается следующим образом: детали представляются в виде вершин графа, а соединения и сопряжения описываются ребрами. Две вершины соединены ребром тогда и только тогда, на соответствующие детали наложена механическая связь. На рис. 1 показана конструкция крепления промежуточного вала цилиндрического редуктора и граф механических связей этой конструкции.
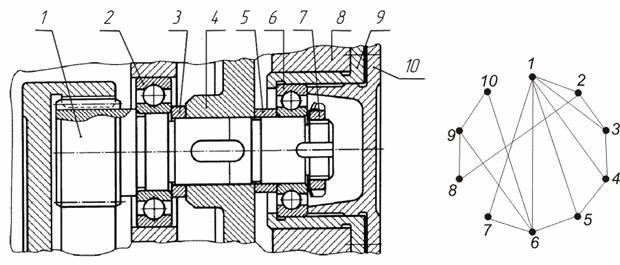
Рис. 1. Промежуточный вал цилиндрического редуктора внутреннего зацепления
Граф механических модель позволяет решать многие задачи размерного и системного анализа конструкций, но, к сожалению, не позволяет точно описать условия базирования. Этот носитель задает бинарное отношение механической связности, тогда как отношение базирования, в общем случае, является многоместным. Действительно, существуют конструктивные решения, когда для точной координации детали требуется реализовать несколько связей одновременно, то есть полный комплект баз включает в себя фиксированную группировку, состоящую из нескольких деталей. В качестве простейшего примера можно привести способ установки подшипника на вал, показанный на рис. 1, когда внутреннее кольцо этой сборочной единицы (6 на рис. 1) позиционируется относительно торца втулки (5 на рис. 1) и наружной поверхности вала (1 на рис. 1). Две эти связи, реализованные совместно, определяют положение подшипника, но ни одна из них в отдельности таким свойством не обладает. Для описания многоместных отношений и отношений переменной местности удобно использовать аппарат гиперграфов. В работах автора предложена и обоснована гиперграфовая модель условий базирования в технических системах [10-13].
Определение 1. Подмножество будем называть геометрически определенным, если положение всех входящих в него деталей определено относительно друг друга согласно комплекту сборочных чертежей и техническим требованиям. Геометрически определенное подмножество является минимальным, если исключение любой детали нарушает свойство взаимной координации составных частей.
Машине или механическому прибору поставим в соответствие изделию гиперграф ![]() , где множество вершин
, где множество вершин ![]() описывает элементы технической системы (детали и комплектующие), множество гиперребер
описывает элементы технической системы (детали и комплектующие), множество гиперребер ![]() представляет минимальные геометрически определенные группировки элементов, а
представляет минимальные геометрически определенные группировки элементов, а ![]() –инцидентор, который связывает гиперребра с входящими в него вершинами. Будем называть эту модель гиперграфом механических связей. На рис. 2 показан гиперграф, описывающий отношения базирования в конструкции крепления промежуточного вала цилиндрического редуктора (см. рис. 1).
–инцидентор, который связывает гиперребра с входящими в него вершинами. Будем называть эту модель гиперграфом механических связей. На рис. 2 показан гиперграф, описывающий отношения базирования в конструкции крепления промежуточного вала цилиндрического редуктора (см. рис. 1).
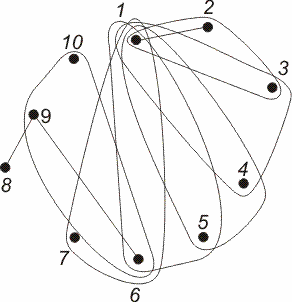
Рис. 2. Гиперграфовая модель отношения базирования
Данная структурная модель показала свою адекватность и высокую содержательность. Множество проектных решений, который принимает технолог при разработке технологического процесса сборки изделия, можно описать в терминах гиперграфа механических связей [11, 13].
Введем определение.
Определение 2. Гиперграф ![]() назовем стягиваемым (s-гиперграфом), если существует последовательность
назовем стягиваемым (s-гиперграфом), если существует последовательность ![]() , для элементов которой выполняются следующие требования:
, для элементов которой выполняются следующие требования:
1. ![]() ;
;
2. ![]() представляет собой одновершинный гиперграф;
представляет собой одновершинный гиперграф;
3. для всех ![]() справедливо соотношение
справедливо соотношение ![]() ;
;
4. каждый элемент последовательности ![]() получается из предыдущего
получается из предыдущего ![]() стягиванием ребра кратности 2,
стягиванием ребра кратности 2, ![]() . Будем называть такое стягивание нормальным.
. Будем называть такое стягивание нормальным.
Условия 1 – 4 описывают процесс сборки изделия как последовательность реализации механических связей. Если отвлечься от технологического содержания сборочных операций, то оказывается, что установка детали заключается в реализации базовых инциденций, которые связывают ее с собранным фрагментом изделия (условие 3). Стартовое состояние процесса задается исходным гиперграфом, финальное состояние – одновершинным гиперграфом (условие 1), в котором реализованы все связи (условие 2). Поскольку собранный фрагмент представляется одной вершиной, то в процессе стягиваний гиперребра высоких степеней «схлопываются» и превращаются гиперребра степени 2 (условие 4).
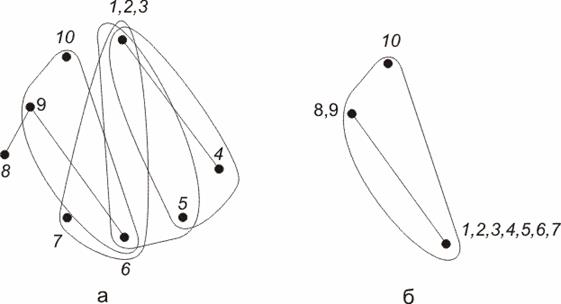
Рис. 3. Гиперграф Hв начале (а) и в конце (б) сборочного процесса
На рис. 3 а показано состояние гиперграфа Hпосле соединения вала (1), подшипника (2) и втулки (3). Гиперребро третьей степени, которое в исходном состоянии объединяло вершины 1, 3 и 4, превратилось в ребро степени два, инцидентное стянутому фрагменту 1,2,3 и вершине 4. На рис. 3 б представлен гиперграф Hпосле реализации 7 операций стягивания ребер.
Значительный практический и научный интерес представляют формулировки необходимых и достаточных условий стягиваемости гиперграфов, задающих механические структуры изделий различных классов. В работах [11, 12] приводится несколько утверждений, относящихся к стягиваемости гиперграфов механических связей изделий, элементы которых ведут себя как абсолютно твердые тела в процессе сборки. Приведем основные результаты.
Утверждение 1. Пусть существует последовательность нормальных стягиваний гиперграфа ![]() , переводящая Hв одновершинный гиперграф без петель. Тогда выполняются условия:
, переводящая Hв одновершинный гиперграф без петель. Тогда выполняются условия:
1. среди ребер Hсуществует по крайне мере одно ребро степени 2;
2. гиперграф является связным;
3. количество вершин ![]() и ребер
и ребер ![]() гиперграфа Hудовлетворяют линейному ограничению
гиперграфа Hудовлетворяют линейному ограничению ![]() .
.
Утверждение 2. Если гиперграф Hне содержит гиперребер, степень которых превышает 3, то условия 1-3 являются достаточными.
Утверждение 3. В общем случае, условия 1-3 являются необходимыми, но не достаточными. Существуют гиперграфы, отвечающие требованиям 1-3, но не допускающие стягивания в смысле определения 1.
Несколько примеров нестягиваемых гиперграфов малой размерности приведены на рис. 4 (образцы а и б изоморфны друг другу).
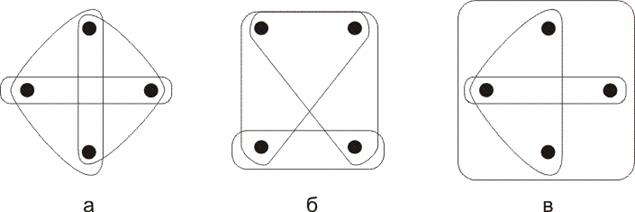
Рис. 4. Нестягиваемые гиперграфы четвертого порядка
Множество неизоморфных нестягиваемых образцов очень быстро растет с увеличением количества вершин. Они состоят преимущественно из ребер высоких степеней (четвертой и выше) и небольшого числа ребер второй степени. Причем последние являются либо мостами, либо соединяют вершины, не принадлежащие разным ребрам высоких степеней. В этом случае стягивание ребра второй степени не приводит к снижению размерности других ребер и появлению индуцированных ребер второй степени, которые, в свою очередь, могут быть стянуты. Это делает невозможным продолжение нормальных стягиваний ребер гиперграфа. На рис. 5 изображены четыре неизоморфных гиперграфа пятого порядка. Для лучшего восприятия третьего сложного примера его ребра нарисованы линиями разного стиля.
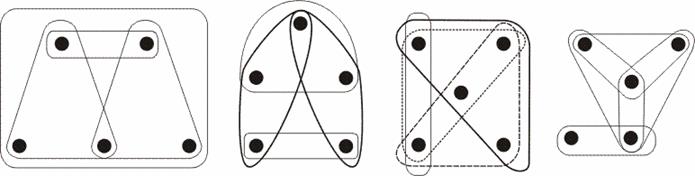
Рис. 5. Нестягиваемые гиперграфы пятого порядка
Поскольку число неизоморфных нестягиваемых подграфов быстро увеличивается с ростом количества вершин, то достаточность стягиваемости гиперграфов общего вида не может быть выражена посредством перечисления запрещенных подструктур.
Сложности с поиском достаточных условий для общего случая в значительной степени вызваны тем, что допускаются гиперебра, степень которых может быть сколь угодно высока. Однако в практике машиностроения и механического приборостроения крайне редко используются конструкторские решения, в которых полный комплект баз состоит даже из трех деталей. Вероятность базирования по четырем и большему числу деталей можно уверенно считать нулевой. Это значит, что гиперграфы, описывающие позиционные механические связи реальных технических систем, состоят из гиперребер степени не выше третьей.
Утверждение 5. Пусть гиперграф ![]() не содержит ребер, степень которых превышает 3. Тогда Hявляется s-гиперграфом тогда и только тогда, когда он удовлетворяет условиям утверждения 1 и не содержит подгиперграфов, гомеоморфных образцу, показанному на рис. 4 а.
не содержит ребер, степень которых превышает 3. Тогда Hявляется s-гиперграфом тогда и только тогда, когда он удовлетворяет условиям утверждения 1 и не содержит подгиперграфов, гомеоморфных образцу, показанному на рис. 4 а.
Итак, структуры механических связей изделий, которые допускают независимую сборку, описываются s-гиперграфами. Свойством независимой сборки могут обладать и некоторые составные части технической системы. Прежде всего, это сборочные единицы разного уровня иерархии, а также сборочные полуфабрикаты – образы, которые «пробегает» изделие в процессе своего изготовления. Структуры механических связей таких подсистем описываются подгиперграфами, которые допускают стягивание в смысле утверждения 1, иными словами – s-подгиперграфами.
Теоретико-решеточная модель собираемости и расчленяемости
Пусть задан гиперграф ![]() , описывающий позиционные механические связи изделия. Пусть гиперграф Hявляется s-гиперграфом. Тогда каждый его s-подгиперграф полностью определяется набором своих вершин, как порожденный в
, описывающий позиционные механические связи изделия. Пусть гиперграф Hявляется s-гиперграфом. Тогда каждый его s-подгиперграф полностью определяется набором своих вершин, как порожденный в ![]() . Для упрощения терминологии введем следующее определение.
. Для упрощения терминологии введем следующее определение.
Определение 3. Стягиваемые подгиперграфы (s-подгиперграфы), принадлежащие стягиваемому гиперграфу H, будем называть просто s-множествами.
Обозначим F(H) совокупность всех s-множеств некоторого стягиваемого гиперграф H. Введем на нем отношение порядка, индуцированное теоретико-множественным включением s-множеств, то есть ![]() . Рассмотрим упорядоченное множество
. Рассмотрим упорядоченное множество ![]() .
.
Утверждение 6. Пусть ![]() – стягиваемый гиперграф. Частично-упорядоченное множество
– стягиваемый гиперграф. Частично-упорядоченное множество ![]() всех s-множеств гиперграфа H, пополненное пустым множеством
всех s-множеств гиперграфа H, пополненное пустым множеством ![]() , является решеткой.
, является решеткой.
Решеткой называется алгебраическая структура, на элементах которой определены две операции: решеточное пересечение ![]() и решеточное объединение
и решеточное объединение ![]() . Эти операции замкнуты и обладают свойствами коммутативности, ассоциативности, идемпотентности и поглощения. Связь между порядковым и алгебраическим толкованиями решетки задаются следующими соотношениями:
. Эти операции замкнуты и обладают свойствами коммутативности, ассоциативности, идемпотентности и поглощения. Связь между порядковым и алгебраическим толкованиями решетки задаются следующими соотношениями: ![]() [14]. Когда алгебраическое толкование решеток важнее порядкового, используют обозначение
[14]. Когда алгебраическое толкование решеток важнее порядкового, используют обозначение ![]() .
.
В данной работе будем рассматривать решетки как хорошо организованные частичные порядки, в которых каждая пара элементов имеет точную верхнюю границу (sup, супремум) и точную нижнюю границу (inf, инфимум). По сравнению с алгебраической формой, порядковое толкование решеток допускает более простую алгоритмизацию основных операций и структур на решетках вида F(H). Например, для поиска решеточного объединения (супремума) требуется найти ближайший к операндам элемент, который превосходит каждый из них. Решеточное пересечение (инфимум) рассчитывается похожим образом. Им служит самый старший из элементов, которые доминируются всеми операндами. Обе задачи сводятся поиску путей на ориентированных графах.
Известны различные способы определения решеток: матричный, аналитический, графовый и др. Для решеток небольших размерностей самой компактной и наглядной формой представления будет диаграмма Хассе. Она строится по следующим простым правилам:
1. если ![]() , то на рисунке элемент aразмещается ниже элемента b;
, то на рисунке элемент aразмещается ниже элемента b;
2. aсоединяется ребром с bтогда и только тогда, когда не существует такого c, что ![]() .
.
На рис. 6 показана решетка ![]() , описывающая структуру s-множеств конструкции крепления вала (см. рис. 1). Рассмотрим основные свойства объектов данного типа на этом примере.
, описывающая структуру s-множеств конструкции крепления вала (см. рис. 1). Рассмотрим основные свойства объектов данного типа на этом примере.
Вершины решетки ![]() описывают s-множества изделия. Наибольшим элементом (или, как иногда говорят, единицей) решетки служит изделие в сборе. Наименьшим элементом (нулем) является пустое множество. Элементы, покрывающие решеточный ноль, представляют собой детали. Решеточным объединением двух элементов из F(H) служит наименьшее по составу s-множество, включающее в себя оба операнда, например
описывают s-множества изделия. Наибольшим элементом (или, как иногда говорят, единицей) решетки служит изделие в сборе. Наименьшим элементом (нулем) является пустое множество. Элементы, покрывающие решеточный ноль, представляют собой детали. Решеточным объединением двух элементов из F(H) служит наименьшее по составу s-множество, включающее в себя оба операнда, например ![]() . Решеточным пересечением двух элементов F(H) является наибольшее по составу s-множество, входящее в оба операнда, например
. Решеточным пересечением двух элементов F(H) является наибольшее по составу s-множество, входящее в оба операнда, например ![]() .
.
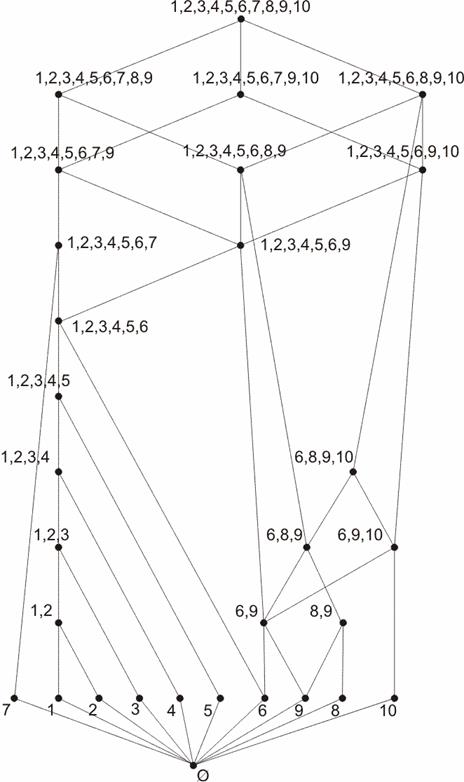
Рис. 6. Диаграмма Хассе решетки s-множеств
Оказалось, что решетки типа ![]() очень содержательны в конструктивном и технологическом смысле. Она представляет все подмножества деталей, между которыми может быть достигнута взаимная скоординированность, заданная структурой механических позиционных связей изделия. Сборочные единицы различного уровня вложенности, узлы, агрегаты, комплекты, комплексы и т.д. – все эти элементы не могут существовать без взаимной координации составных частей. Поэтому они имеют решеточные образы в
очень содержательны в конструктивном и технологическом смысле. Она представляет все подмножества деталей, между которыми может быть достигнута взаимная скоординированность, заданная структурой механических позиционных связей изделия. Сборочные единицы различного уровня вложенности, узлы, агрегаты, комплекты, комплексы и т.д. – все эти элементы не могут существовать без взаимной координации составных частей. Поэтому они имеют решеточные образы в ![]() .
.
Решетку F(H) можно рассматривать как универсальную порождающую среду для генерации проектных решений в сборочном и ремонтном технологических переделах. Множество сборочных операций и проектных решений можно описать в терминах данной структуры. Приведем несколько важнейших примеров.
Любой путь в ![]() из минимального элемента (
из минимального элемента (![]() ) в максимальный (H) представляет собой описание последовательности сборки, которую допускает изделие по условиям базирования. Такие пути в теории решеток называются (0,1)-цепями. Множество всех таких путей образует исходное множество альтернатив в задаче выбора рациональной последовательности сборки в заданной технологической системе.
) в максимальный (H) представляет собой описание последовательности сборки, которую допускает изделие по условиям базирования. Такие пути в теории решеток называются (0,1)-цепями. Множество всех таких путей образует исходное множество альтернатив в задаче выбора рациональной последовательности сборки в заданной технологической системе.
Если путь длина (0,1)-цепи равна ![]() |X|, то она является описанием последовательности сборки изделия без предварительного разбиения на сборочные единицы. В противном случае, цепь служит моделью последовательности сборки с разузлованием. Например, цепь длины 10
|X|, то она является описанием последовательности сборки изделия без предварительного разбиения на сборочные единицы. В противном случае, цепь служит моделью последовательности сборки с разузлованием. Например, цепь длины 10
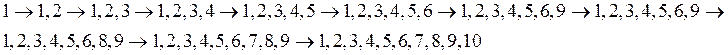
является описанием линейной последовательности сборки (без разбиения на сборочные единицы, а цепь длины 5
![]()
соответствует последовательности, в которой участвуют предварительно собранные узлы ![]() .
.
Важнейшим проектным решением технической подготовки механосборочного производства является способ разбиения изделия на сборочные единицы. В классической монографии, которая специалистами по сборочному переделу считается самым авторитетным источником среди публикаций на русском языке по данному предмету, утверждается: «...Технологическая схема сборки является основным оперативным документом, по которому персонал сборочного цеха знакомится с последовательностью сборки новой машины, организует выполнение сборочного процесса, производит комплектование машины, подачу сборочных единиц и деталей в надлежащей последовательности, ведет учет, планирует производство, вносит усовершенствования в конструкцию, технологический процесс и организацию производства машины» [15].
Технологические документы, в которых фиксируется декомпозиция конструкции на независимо собираемые подмножества деталей, имеют различные наименования, зависящие от отраслевой принадлежности и класса изделия, например, схема членения, граф разузлования, схема сборки, схема сборочного состава (ССС) и др. В этой работе будем использовать последнее наименование.
Решетка ![]() содержит всю информацию, необходимую для синтеза схем сборочного состава. В работе [13] предложен алгебраический способ синтеза ССС, основанный на использовании решеточных операций и конгруэнций, порожденных разбиениями атомов решетки. К сожалению, этот подход оказался не очень эффективным с вычислительной точки зрения. Рассмотрим более наглядный и менее ресурсоемкий способ математического описания ССС, основанный на использовании порядковых терминов и отношений.
содержит всю информацию, необходимую для синтеза схем сборочного состава. В работе [13] предложен алгебраический способ синтеза ССС, основанный на использовании решеточных операций и конгруэнций, порожденных разбиениями атомов решетки. К сожалению, этот подход оказался не очень эффективным с вычислительной точки зрения. Рассмотрим более наглядный и менее ресурсоемкий способ математического описания ССС, основанный на использовании порядковых терминов и отношений.
Легко согласиться с тем, что все конструктивно реализуемые ССС представляются в виде деревьев, вписанных в решетку F(H). Основная трудность заключается в корректном определении таких деревьев. Приведем несколько определений из теории упорядоченных множеств [8]. Упорядоченное множество ![]() называется направленным вверх, если любые два его элемента имеют верхнюю границу. Пусть
называется направленным вверх, если любые два его элемента имеют верхнюю границу. Пусть ![]() – конечная решетка. Ортогональной системой решетки называется подмножество элементов, обладающее следующими свойствами: (1) подмножество не содержит нуля, (2) пересечение любых двух элементов подмножества равно нулю.
– конечная решетка. Ортогональной системой решетки называется подмножество элементов, обладающее следующими свойствами: (1) подмножество не содержит нуля, (2) пересечение любых двух элементов подмножества равно нулю.
Утверждение 7. Упорядоченное подмножество ![]() решетки
решетки ![]() является математическим описанием схемы сборочного состава, если выполняются следующие условия:
является математическим описанием схемы сборочного состава, если выполняются следующие условия:![]()
1. упорядоченное множество ![]() является направленным вверх;
является направленным вверх;
2. ![]() включает в себя все атомы решетки
включает в себя все атомы решетки ![]() ;
;
3. любая антицепь (множество несравнимых элементов) в ![]() является ортогональным множеством в
является ортогональным множеством в ![]() .
.
Приведем формальные аргументы в пользу этого очень важного утверждения. Диаграмма Хассе упорядоченного множества ![]() является связным ориентированным графом, вершинами которого служат s-множества решетки
является связным ориентированным графом, вершинами которого служат s-множества решетки ![]() . Любая пара несравнимых элементов из
. Любая пара несравнимых элементов из ![]() есть ортогональное семейство в
есть ортогональное семейство в ![]() . Кроме того, диаграмма Хассе множества
. Кроме того, диаграмма Хассе множества ![]() не содержит транзитивно замыкающих дуг по определению, поэтому она представляет собой ориентированное корневое дерево. Его корнем служит образ изделия X, а висячими вершинами – атомы
не содержит транзитивно замыкающих дуг по определению, поэтому она представляет собой ориентированное корневое дерево. Его корнем служит образ изделия X, а висячими вершинами – атомы ![]() (образы деталей).
(образы деталей).
Пусть Y– произвольный элемент из ![]() , не равный атому, то есть
, не равный атому, то есть ![]() . Рассмотрим подмножество
. Рассмотрим подмножество ![]() всех элементов из M, которые накрываются элементом Y, Y>Xi. Это подмножество представляет собой антицепь в M. Действительно, пусть существуют
всех элементов из M, которые накрываются элементом Y, Y>Xi. Это подмножество представляет собой антицепь в M. Действительно, пусть существуют ![]() такие, что
такие, что ![]() . Тогда
. Тогда ![]()
![]() . Что противоречит предположению о накрытии Yвсех элементов из
. Что противоречит предположению о накрытии Yвсех элементов из ![]() .
.
По условию 3 утверждения 7 антицепь ![]() является ортогональным множеством. Покажем, что
является ортогональным множеством. Покажем, что ![]() . Предположим обратное и образуем разность
. Предположим обратное и образуем разность ![]() . Пусть
. Пусть ![]() – некоторый атом. Этот элемент принадлежит Mпо исходному предположению. Порядок в Mиндуцирован теоретико-множественным включением, поэтому для любого
– некоторый атом. Этот элемент принадлежит Mпо исходному предположению. Порядок в Mиндуцирован теоретико-множественным включением, поэтому для любого ![]() такого, что
такого, что ![]() .
.
Рассмотрим ![]() такое, что
такое, что ![]() . Так как
. Так как ![]() , то эти элементы сравнимы, а именно
, то эти элементы сравнимы, а именно ![]() . Отсюда следует, что x||Y, то есть xи Yобразуют антицепь в M. Любая антицепь в
. Отсюда следует, что x||Y, то есть xи Yобразуют антицепь в M. Любая антицепь в ![]() является ортогональной системой, поэтому разность
является ортогональной системой, поэтому разность ![]() представляет собой разбиение для любого элемента
представляет собой разбиение для любого элемента ![]() , не равного атому.
, не равного атому.
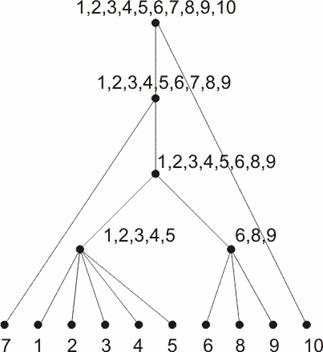
Рис.7. Упорядоченное подмножество ![]()
На рис.7. показано одно из упорядоченных подмножеств ![]() решетки
решетки ![]() , (см. рис. 6), удовлетворяющих всем условиям утверждения 7. Данный частичный порядок является описанием одной из возможных схем сборочного состава, которые допускает конструкция, показанная на рис. 1. Эта схема состоит из двух сборочных единиц 1.2.3.4.5 и 6,8,9, а также деталей 7 и 10, входящих непосредственно в изделие.
, (см. рис. 6), удовлетворяющих всем условиям утверждения 7. Данный частичный порядок является описанием одной из возможных схем сборочного состава, которые допускает конструкция, показанная на рис. 1. Эта схема состоит из двух сборочных единиц 1.2.3.4.5 и 6,8,9, а также деталей 7 и 10, входящих непосредственно в изделие.
Приведенными примерами не исчерпывается технологическое содержание решетки ![]() . В частности, она дает всю необходимую информацию для синтеза последовательностей сборки с промежуточной разборкой отдельных узлов или агрегатов. Такие последовательности применяются в тех случаях, когда необходима пробная сборка с последующей разборкой узла или всего изделия. Пробная сборка используется для пригонки отдельных составных частей, проведения испытаний, выполнения ответственных контрольных работ и др.
. В частности, она дает всю необходимую информацию для синтеза последовательностей сборки с промежуточной разборкой отдельных узлов или агрегатов. Такие последовательности применяются в тех случаях, когда необходима пробная сборка с последующей разборкой узла или всего изделия. Пробная сборка используется для пригонки отдельных составных частей, проведения испытаний, выполнения ответственных контрольных работ и др.
Практика показала, что задачи синтеза многих проектных решений на этапе технологической подготовки механосборочного производства не могут быть поставлены как оптимизационные задачи с четкими критериями оптимальности и ограничениями. Чаще они формулируются в виде задач принятия решений (ЗПР), где окончательный выбор остается за ЛПР, функции которого выполняет технолог или технологической бюро. В постановку любой ЗПР входит некоторое операциональное поле – исходное множество альтернатив (ИМА), из которых ЛПР выбирает (за одни шаг или в процессе некоторой многошаговой процедуры) рациональное подмножество вариантов. Задачи синтеза рациональной последовательности сборки и схемы сборочного состава являются задачами данного типа. Решетка ![]() позволяет найти ИМА, необходимые для генерации рациональных последовательностей и схем в заданных производственных условиях.
позволяет найти ИМА, необходимые для генерации рациональных последовательностей и схем в заданных производственных условиях.
Заключение
Важнейшими проектными решениями технологической подготовки машиностроительного производства являются последовательность сборки изделия и его декомпозиция на независимо собираемые сборочные единицы. Необходимым условиям существования этих решений служит взаимная координация деталей, входящих в сборочные единицы и сборочные полуфабрикаты. Координация фрагментов изделия достигается базированием деталей относительно друг друга. Отношение базирования является многоместным и не может быть точно описано в терминах графов. Адекватной моделью базирования при сборке является гиперграф механических связей. По данной модели можно построить решетку F(H), которая служит универсальной порождающей средой для генерации проектных решений, требующих взаимной координации своих составных частей. Важнейшими из таких решений являются последовательность сборки изделия и схема сборочного состава. Решетка F(H) позволяет синтезировать множество всех последовательностей и схем, которые допускает конструкция изделия. Эти множества служат исходными множествами альтернатив в задачах синтеза рациональных последовательностей и схем с учетом дополнительным технологических, производственных и др. условий.
Списоклитературы
1. Baldwin D.F., Abell, T.E., Lui M.M., De Fazio T.L., Whitney D.E. An integrated computer aid for generating and evaluating assembly sequences for mechanical products // IEEE Transactions on Robotics and Automation. 1991. Vol. 7, iss. 1. P.78-94. DOI: 10.1109/70.68072
2. Whitney D.E. Mechanical Assemblies: Their Design, Manufacture, and Role in Product Development. Oxford University Press, 2004. 518 p.
3. De Fazio T.L., Whitney D.E. Simplified generation of all mechanical assembly sequences // IEEE Journal of Robotics and Automation. 1987. Vol. 3, iss. 6. P. 640-658. DOI: 10.1109/JRA.1987.1087132
4. Dini G., Failli F., Lazzerini B., Marcelloni F. Generation of optimized assembly sequences using genetic algorithms // Annals of the CIRP. 1999. Vol. 48. P. 17-20.
5. Antonsson E.K., Cagan J. Formal Engineering Design Synthesis. Cambridge University Press, 2005. 500 p.
6. Homem De Mello L.S., Sanderson A.C. A correct and complete algorithm for the generation of mechanical assembly sequences // IEEE Transactions on Robotics and Automation. 1991. Vol. 7, iss. 2. P. 228-240. DOI: 10.1109/70.75905
7. Homem De Mello L.S., Lee S. Computer-Aided Mechanical Assembly Planning. Springer, 1991. 464 p. (Ser. The Springer International Series in Engineering and Computer Science; vol. 148). DOI: 10.1007/978-1-4615-4038-0
8. Айгнер М. Комбинаторная теория. М.: Мир, 1982. 558 с.
9. Бабушкин А.И., Башта А.А., Белов А.И., Душин Б.И. Оптимизация последовательности сборки // Автоматика и телемеханика. 1977. № 9. С. 77-82.
10. Божко А.Н., Бетин Е А. Анализ стягиваемости гиперграфов // Информационные технологии. 2005. № 5. С. 6-12.
11. Божко А.Н. Моделирование механических связей изделия. Условия стягиваемости // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2011. № 5. Режим доступа: http://technomag.bmstu.ru/doc/182518.html (дата обращения 01.09.2013).
12. Божко А.Н. Моделирование механических связей изделия // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2011. № 3. Режим доступа: http://technomag.bmstu.ru/doc/168373.html (дата обращения 01.09.2013)
13. Божко А.Н. Моделирование позиционных связей в механических системах // Информационные технологии. 2012. № 10. С. 27-33.
14. Гретцер Г. Общая теория решеток. М.: Мир, 1982. 456 с.
15. Новиков М.П. Основы технологии сборки машин и механизмов. М.: Машиностроение, 1980. 298 с.
16. Павлов В.В. Основы автоматизации проектирования технологических процессов сборки летательных аппаратов: учеб. пособие. М.: Изд-во МАТИ, 1975. 98 с.
17. Плотко В.П. Определение последовательности сборки сборочных единиц // Автоматизированное проектирование технических систем и процессов. Минск: ИТК АН БССР, 1979. С. 11-14.
18. Сборка и монтаж изделий машиностроения: справочник. В 2 т. Т. 2 / Под ред. В.С. Корсакова, В.К. Замятина. М.: Машиностроение, 1983. 360 с.
19. Солонин И.С. Солонин C.И. Расчет сборочных и технологических размерных цепей. М.: Машиностроение, 1980. 112 с.
20. Тимковский В.Б. Дискретная математика в мире станков и деталей. М.: Наука, 1992. 145 с.
21. Харари Ф. Теория графов / Под ред. Г.П. Гаврилова. 2-е изд. М.: Едиториал УРСС, 2003. 296 с.
Публикации с ключевыми словами: сборочная единица, сборка, граф, базирование, гиперграф, механическая связь, последовательность сборки, решетка, упорядоченное множество, сопряжение, стягивание, схема сборочного состава
Публикации со словами: сборочная единица, сборка, граф, базирование, гиперграф, механическая связь, последовательность сборки, решетка, упорядоченное множество, сопряжение, стягивание, схема сборочного состава
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



