научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2013
DOI: 10.7463/1113.0621065
УДК 539.3
Россия, МГТУ им. Н.Э. Баумана
Введение. Полимерные композиционные материалы находят широкое применение при создании тепловой защиты аэрокосмических летательных аппаратов и возвращаемых аппаратов. При проектировании теплозащитных материалов к ним предъявляется комплекс требований: обладания относительно высокими теплопрочностными свойствами, пониженной теплопроводностью, пониженной плотностью и другими. В [1] был предложен аналитический подход к проектированию оптимальной микроструктуры теплозащитных композитов для обеспечения выполнения комплекса требуемых эксплуатационных характеристик материалов. В данной работе предложено развитие этого метода с учетом более детального рассмотрения микронапряжений и тепловых полей в композитах, и с применением метода конечного элемента для решения локальных задач для расчета микрохарактеристик композитов, возникающих при использовании метода асимптотического осреднения композитов с периодической структурой [2-7].
Постановка задачи оптимального проектирования композиционного материала. Рассмотрим композиционный материал, состоящий из изотропной матрицы и N-1 изотропного наполнителя со следующими характеристиками: ρα – плотность; Eα – модуль Юнга; να – коэффициент Пуассона; Gα – модуль сдвига; ![]() – пределы прочности при растяжении, сжатии и сдвиге, соответственно; λα –коэффициент теплопроводности. Здесь индекс
– пределы прочности при растяжении, сжатии и сдвиге, соответственно; λα –коэффициент теплопроводности. Здесь индекс ![]() соответствует наполнителю с номером α, а индекс α=N соответствует матрице. Объемные концентрации компонент обозначим φα, для них выполняется очевидное соотношение:
соответствует наполнителю с номером α, а индекс α=N соответствует матрице. Объемные концентрации компонент обозначим φα, для них выполняется очевидное соотношение:  .
.
Введем обозначения для эффективных характеристик композиционного материала: ![]() – плотность;
– плотность; ![]() – компоненты тензора эффективных модулей упругости;
– компоненты тензора эффективных модулей упругости; ![]() – эффективные пределы прочности композита при одноосных растяжениях и сжатиях вдоль трех ортогональных осей, соответственно;
– эффективные пределы прочности композита при одноосных растяжениях и сжатиях вдоль трех ортогональных осей, соответственно; ![]() – компоненты эффективного тензора теплопроводности. Все эти эффективные характеристики зависят от объемных концентраций компонентов, а также от их геометрической формы. Будем далее полагать, что геометрическая форма может быть параметризована только с помощью одного числового параметра. Это допущение является достаточно сильным, ему удовлетворяет ограниченное число геометрических форм армирующих компонентов композитов, например, дисперсные частицы с шаровой формой, частицы в виде микросфер с постоянной толщиной стенок микросфер, цилиндрические волокна и некоторые другие типы, в которых меняется только один геометрический параметр. Тогда для такого типа однопараметрических композитов их эффективные характеристики могут быть представлены как функции только концентраций компонентов:
– компоненты эффективного тензора теплопроводности. Все эти эффективные характеристики зависят от объемных концентраций компонентов, а также от их геометрической формы. Будем далее полагать, что геометрическая форма может быть параметризована только с помощью одного числового параметра. Это допущение является достаточно сильным, ему удовлетворяет ограниченное число геометрических форм армирующих компонентов композитов, например, дисперсные частицы с шаровой формой, частицы в виде микросфер с постоянной толщиной стенок микросфер, цилиндрические волокна и некоторые другие типы, в которых меняется только один геометрический параметр. Тогда для такого типа однопараметрических композитов их эффективные характеристики могут быть представлены как функции только концентраций компонентов:
 ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . (1)
. (1)
Аналитическое выражение для функций (1) при любых структурах армирования возможно только для плотности (линейная функция), для остальных функций эти зависимости имеют сложный нелинейный вид, аналитически они могут быть вычислены только приближенно ([2]), или для очень простых микроструктур , например, слоистых ([1]). Методика численного конечно-элементного вычисления функций (1) представлена в следующих разделах статьи.
Зададим ограничения на эффективные характеристики композита:
![]() , (2)
, (2)
где ![]() – некоторые числовые константы – ограничения, задаваемые проектировщиком композиционного материала.
– некоторые числовые константы – ограничения, задаваемые проектировщиком композиционного материала.
Задачей оптимального проектирования микроструктуры композита будем называть задачу минимизации плотности композита
 (3)
(3)
при выполнении ограничений (2). Задача (3) с ограничениями (2) представляет собой задачу поиска минимума линейной функции в условиях нелинейных ограничений.
Методика решения вспомогательной задачи расчета эффективных характеристик композита. Для нахождения функций ![]() и
и ![]() - эффективных характеристик упругости и теплопроводности композита применим метод асимптотического осреднения [5-12], согласно которому для нахождения этих функций необходимо решить специальные краевые трехмерные задачи теории упругости и теории теплопроводности на 1/8 части ячейки периодичности композита. Эти задачи называются локальными задачами Lpq и Lq , соответственно.
- эффективных характеристик упругости и теплопроводности композита применим метод асимптотического осреднения [5-12], согласно которому для нахождения этих функций необходимо решить специальные краевые трехмерные задачи теории упругости и теории теплопроводности на 1/8 части ячейки периодичности композита. Эти задачи называются локальными задачами Lpq и Lq , соответственно.
В соответствии с [7] локальные задачи Lpq теории упругости имеют вид:
 (4)
(4)
где ΣαN – поверхности контакта компонентов композита; Σs – координатные плоскости, ![]() ;
; ![]() –торцевые поверхности ячейки периодичности, имеющей форму единичного куба, s=1,2,3;
–торцевые поверхности ячейки периодичности, имеющей форму единичного куба, s=1,2,3; ![]() - безразмерные координаты, изменяющиеся в единичном кубе (локальные координаты),
- безразмерные координаты, изменяющиеся в единичном кубе (локальные координаты), ![]() ,
, ![]() ,
, ![]() – перемещения, напряжения (микронапряжения) и деформации в компонентах композита Vα,
– перемещения, напряжения (микронапряжения) и деформации в компонентах композита Vα, ![]() – тензоры модулей упругости компонентов, вычисляемые через упругие константы Eα , να , Gα изотропных компонентов стандартным образом [13], /j – производная по локальной координате
– тензоры модулей упругости компонентов, вычисляемые через упругие константы Eα , να , Gα изотропных компонентов стандартным образом [13], /j – производная по локальной координате ![]() ,
, ![]() - компоненты вектора нормали. Функции
- компоненты вектора нормали. Функции ![]() удовлетворяют следующим граничным условиям на
удовлетворяют следующим граничным условиям на ![]() :
:
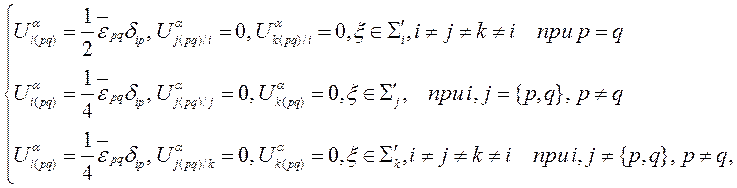 (5)
(5)
где ![]() – заданные средние деформации (макродеформациии) композита.
– заданные средние деформации (макродеформациии) композита.
Локальная задача Lpтеории теплопроводности имеет вид:
 (6)
(6)
где![]() – компоненты вектора теплового потока,
– компоненты вектора теплового потока, ![]() –компоненты вектора градиента температуры,
–компоненты вектора градиента температуры, ![]() - температура. Граничные условия для задачи Lp теории теплопроводности имеют вид:
- температура. Граничные условия для задачи Lp теории теплопроводности имеют вид:
 (7)
(7)
![]() – заданные компоненты осредненного вектора градиента температуры.
– заданные компоненты осредненного вектора градиента температуры.
Локальные задачи (4),(5) и (6),(7) для каждых значений p,q={1,2,3} решаем методом конечного элемента [7], в результате решения этих задач вычисляем поля микронапряжений ![]() и тепловых микропотоков
и тепловых микропотоков ![]() для всей 1/8 ячейки периодичности
для всей 1/8 ячейки периодичности  . С помощью этих полей вычисляем эффективные характеристики композита по формулам:
. С помощью этих полей вычисляем эффективные характеристики композита по формулам:
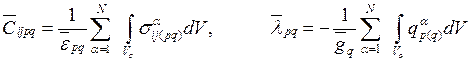 , (8)
, (8)
Осуществляя описанным выше методом решение локальных задач Lpq и Lp при различных значениях концентраций компонентов ![]() , с помощью формул (8) находим искомые функции (1) – зависимости эффективных характеристик композита от концентраций
, с помощью формул (8) находим искомые функции (1) – зависимости эффективных характеристик композита от концентраций ![]() его структурных компонентов.
его структурных компонентов.
Методика расчета эффективных констант прочности композита. Для вычисления пределов прочности ![]() и
и ![]() композита используем следующую методику, предложенную в [8]. Вычислим поля компонент тензоров концентрации напряжений Bijkl(ξs) в компонентах композита, которые связывают микронапряжения со средними напряжениями
композита используем следующую методику, предложенную в [8]. Вычислим поля компонент тензоров концентрации напряжений Bijkl(ξs) в компонентах композита, которые связывают микронапряжения со средними напряжениями
![]() , (9)
, (9)
где 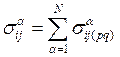 . Компоненты этих тензоров вычисляются по формулам:
. Компоненты этих тензоров вычисляются по формулам:
![]() , (10)
, (10)
где ![]() – компоненты тензора эффективных упругих податливостей композита, обратного к эффективному тензору модулей упругости
– компоненты тензора эффективных упругих податливостей композита, обратного к эффективному тензору модулей упругости ![]() (8), а поля компонент тензоров
(8), а поля компонент тензоров ![]()
![]() - локальных модулей упругости, вычисляются с помощью соотношения
- локальных модулей упругости, вычисляются с помощью соотношения
 . (11)
. (11)
В [8] был предложен метод расчета первичного разрушения композитов на основе критериев прочности Малмейстера-Ву, а в [14] был исследован критерий прочности Писаренко-Лебедева [15]. В данной работе использован критерий прочности Малмейстера-Ву, согласно которому будем считать, что происходит разрушение в некоторой точке материала, принадлежащей компоненте α, если выполняется критерий прочности (условие разрушения)
![]() , (12)
, (12)
здесь обозначены ![]() - среднее напряжение и
- среднее напряжение и ![]() -интенсивность напряжений
-интенсивность напряжений
![]() , (13)
, (13)
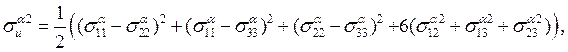
а ![]() - параметры прочности материала компоненты α , определяемые по формулам
- параметры прочности материала компоненты α , определяемые по формулам
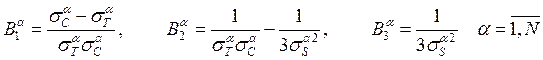 . (14)
. (14)
Рассмотрим процесс простого (пропорционального) нагружения в 6-ти мерном пространстве макронапряжений ![]() , при котором компоненты макронапряжений изменяются пропорционально одному параметру
, при котором компоненты макронапряжений изменяются пропорционально одному параметру ![]() , т.е.
, т.е. ![]() . Если осуществляется одноосное нагружение, то среди компонент тензора
. Если осуществляется одноосное нагружение, то среди компонент тензора ![]() имеется только одна ненулевая компонента
имеется только одна ненулевая компонента![]() , т.е.
, т.е. 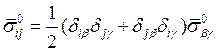 . Будем называть точку
. Будем называть точку ![]() ячейки периодичности композита точкой первоначального разрушения, а напряжение
ячейки периодичности композита точкой первоначального разрушения, а напряжение ![]() - первоначальным пределом прочности композита при нагружении по направлению
- первоначальным пределом прочности композита при нагружении по направлению ![]() в 6-ти мерном пространстве, если для некоторого значения
в 6-ти мерном пространстве, если для некоторого значения ![]() выполняется условие
выполняется условие
![]() , (15)
, (15)
а для значений ![]() выполняются условия
выполняются условия ![]() для всех значений
для всех значений ![]() . Определение (15) дает конструктивный способ нахождения первоначального предела прочности. Для этого необходимо решить задачи Lpq теории упругости, в соответствии с формулами (8)-(9) вычислить тензор концентрации напряжений, задать малое начальное значение параметра нагружения
. Определение (15) дает конструктивный способ нахождения первоначального предела прочности. Для этого необходимо решить задачи Lpq теории упругости, в соответствии с формулами (8)-(9) вычислить тензор концентрации напряжений, задать малое начальное значение параметра нагружения ![]() , и последовательно увеличивать его, пока при некотором его значении
, и последовательно увеличивать его, пока при некотором его значении ![]() в некоторой точке ячейки периодичности композита не будет выполнен критерий (15).
в некоторой точке ячейки периодичности композита не будет выполнен критерий (15).
Для определения пределов не первоначального, а полного разрушения композита, будем использовать следующий алгоритм. Назовем трещиной непрерывную область композита, во всех точках которой выполняется критерий (15), а полным разрушением композита в целом будем называть ситуацию, когда существует по крайней мере одна трещина, соединяющая противоположные грани ячейки периодичности. Минимальное значение напряжение ![]() , приводящее к полному разрушению ячейки периодичности, будем называть эффективным пределом прочности композита при нагружении по лучу
, приводящее к полному разрушению ячейки периодичности, будем называть эффективным пределом прочности композита при нагружении по лучу ![]() .
.
Алгоритм расчета пределов прочности композита был следующим.
1) Выбираем произвольные значения макродеформаций ![]() . Решая задачи Lpq (4),(5) для p,q=1,2,3 методом конечных элементов, по формулам (10),(11) вычислим тензор концентрации напряжений Bijkl(ξ).
. Решая задачи Lpq (4),(5) для p,q=1,2,3 методом конечных элементов, по формулам (10),(11) вычислим тензор концентрации напряжений Bijkl(ξ).
2) Выбираем луч ![]() в 6-мерном пространстве макронапряжений, по которому будет осуществляться нагружение композита. Выбираем начальное малое значение параметра нагружения
в 6-мерном пространстве макронапряжений, по которому будет осуществляться нагружение композита. Выбираем начальное малое значение параметра нагружения ![]() , при котором критерий (15) первоначального разрушения композита заведомо не выполняется. Далее осуществляем итерационный цикл по параметру нагружения, на каждом m-м шаге последовательно увеличивая значения параметра
, при котором критерий (15) первоначального разрушения композита заведомо не выполняется. Далее осуществляем итерационный цикл по параметру нагружения, на каждом m-м шаге последовательно увеличивая значения параметра ![]() . На каждом m-м шаге решения локальных задач Lpq не требуется, а проверяется только выполнение условия (15). Значение
. На каждом m-м шаге решения локальных задач Lpq не требуется, а проверяется только выполнение условия (15). Значение ![]() , при котором впервые выполняется условие (15), соответствует первоначальному пределу прочности
, при котором впервые выполняется условие (15), соответствует первоначальному пределу прочности ![]() .
.
3) Далее увеличиваем значение параметра нагружения ![]() . Конечные элементы, в которых выполнен критерий (15), будем трактовать как новую компоненту композита с номером N+1 и называть разрушенной компонентой. При этом модуль упругости EN+1 разрушенной компоненты полагается существенно меньшим, чем модуль упругости всех остальных компонентов: EN+1<<Eα при α≠N+1.
. Конечные элементы, в которых выполнен критерий (15), будем трактовать как новую компоненту композита с номером N+1 и называть разрушенной компонентой. При этом модуль упругости EN+1 разрушенной компоненты полагается существенно меньшим, чем модуль упругости всех остальных компонентов: EN+1<<Eα при α≠N+1.
4) При ![]() на каждом шаге итерации пересчитываем значение эффективного модуля упругости
на каждом шаге итерации пересчитываем значение эффективного модуля упругости ![]() по формуле (8), в которой напряжения
по формуле (8), в которой напряжения ![]() и средние деформации
и средние деформации ![]() берутся с предыдущего шага итерации :
берутся с предыдущего шага итерации :
 (16)
(16)
затем вычисляется новые средние значения деформации ![]() на m-м шаге
на m-м шаге
![]() ,
, ![]() ,
, ![]() . (17)
. (17)
С этими значениями ![]() решается локальная задача (4), (5) на m-м шаге итерации, по ее результатам вычисляются компоненты
решается локальная задача (4), (5) на m-м шаге итерации, по ее результатам вычисляются компоненты![]() тензоров микронапряжений на m-м шаге.
тензоров микронапряжений на m-м шаге.
5) Далее осуществляется проверка выполнения критерия (15) в каждом не разрушенном конечном элементе для шага итерации m. В случае выполнения условия (15) для дополнительных КЭ, разрушенная область композита увеличивается за счет этих КЭ и далее осуществляется переход к следующему шагу итерации.
6) Эффективный предел прочности композита ![]() будет соответствовать ситуации, когда разрушенные конечные элементы сформируют трещину, соединяющую противоположные грани ячейки периодичности.
будет соответствовать ситуации, когда разрушенные конечные элементы сформируют трещину, соединяющую противоположные грани ячейки периодичности.
7) Описанную процедуру проведем для 6 различных лучей нагружения ![]() , соответствующих одноосному растяжению и сжатию вдоль 3-х координатных осей ξi , т.е. выбирая значения
, соответствующих одноосному растяжению и сжатию вдоль 3-х координатных осей ξi , т.е. выбирая значения ![]() равными:
равными: ![]() и
и ![]() ,
, ![]() . В результате получим эффективные пределы прочности композита
. В результате получим эффективные пределы прочности композита ![]() при растяжении и сжатии,
при растяжении и сжатии, ![]() , соответственно.
, соответственно.
Алгоритм метода численного решения задачи оптимального проектирования.
Рассмотрим далее случай, когда имеется только одна армирующая компонента композита с концентрацией ![]() . Для численного решения задачи оптимального проектирования (1)-(3) композиционного материала с одной армирующей компонентой применим следующий алгоритм.
. Для численного решения задачи оптимального проектирования (1)-(3) композиционного материала с одной армирующей компонентой применим следующий алгоритм.
Задачу условной минимизации (1)-(3) представим в виде задачи безусловной минимизации с помощью метода барьерных функций [16]. С учетом ограничений (2) введем барьерную функцию
 . (18)
. (18)
Тогда задача (1)-(3) сводится к задаче безусловной минимизации
![]() , (19)
, (19)
которая, в свою очередь, сводится к последовательности следующих задач минимизации
![]() (20)
(20)
с критерием остановки
rkR(φk+1)<ε (21)
для заранее определенного ε.
Барьерная функция (18) имеет нелинейный характер из-за присутствия функций ![]() , для решения каждой из задач (20) будем пользоваться методом Хука-Дживса. В качестве начальной точки для метода барьерных функций требуется точка, заведомо не удовлетворяющая ограничениям. В качестве такой точки выберем решение задачи (3) без ограничений (2):
, для решения каждой из задач (20) будем пользоваться методом Хука-Дживса. В качестве начальной точки для метода барьерных функций требуется точка, заведомо не удовлетворяющая ограничениям. В качестве такой точки выберем решение задачи (3) без ограничений (2): ![]() . В случае, если φ(0) удовлетворяет ограничениям (2), то, очевидно, является точным решением исходной задачи (1)-(3). В противном случае φ(0) можно использовать в качестве начальной точки процесса оптимизации. Таким образом, решение последовательности задач (13) с начальной точкой φ(0) и критерием остановки (21) является решением исходной задачи (1)-(3).
. В случае, если φ(0) удовлетворяет ограничениям (2), то, очевидно, является точным решением исходной задачи (1)-(3). В противном случае φ(0) можно использовать в качестве начальной точки процесса оптимизации. Таким образом, решение последовательности задач (13) с начальной точкой φ(0) и критерием остановки (21) является решением исходной задачи (1)-(3).
Итерационную процедуру вычисления эффективных функций (2), описанную в предыдущих разделах, основанную на применении методов МКЭ, используем на каждом шаге оптимизации структуры.
Результаты численного моделирования. Численные расчеты проводились для дисперсно-армированного композита с изотропной матрицей и одним изотропным наполнителем, представляющим собой тонкие микросферы (рис. 1).

Рис. 1. Изображение 1/8 ячейки периодичности дисперсно-армированного композита на основе микросфер.
В процессе расчета для каждой концентрации наполнителя ячейка периодичности разбивалась приблизительно на 400 тысяч конечных элементов. Разбиение проводилось с помощью свободно распространяемого программного продукта Netgen 4.4. Локальные задачи для поиска эффективных характеристик решались в программном комплексе GCD, разрабатываемом на кафедре ФН-11 МГТУ им. Н.Э. Баумана.
В качестве материала тонкой оболочки микросфер было использовано стекло с характеристиками: ρ1=2600 кг/м3, E1=70 ГПа, ν1=0,2, λ1=0,7 Вт/(м·К), ![]() ,
, ![]() ,
, ![]() ; в качестве матрицы рассматривалось кремнийорганическое связующее со следующими характеристиками: ρ2=1100 кг/м3, E2=2 ГПа, ν2=0,35, λ2=0,2 Вт/(м·К),
; в качестве матрицы рассматривалось кремнийорганическое связующее со следующими характеристиками: ρ2=1100 кг/м3, E2=2 ГПа, ν2=0,35, λ2=0,2 Вт/(м·К), ![]() ,
, ![]() ,
, ![]() . Вследствие симметрии структуры рассмотренного типа композита относительно всех 3-х координатных направлений, он будет обладать изотропными эффективными свойствами, т.е. все эффективные модули упругости
. Вследствие симметрии структуры рассмотренного типа композита относительно всех 3-х координатных направлений, он будет обладать изотропными эффективными свойствами, т.е. все эффективные модули упругости ![]() композита совпадают, совпадают также все 3 коэффициента теплопроводности
композита совпадают, совпадают также все 3 коэффициента теплопроводности ![]() , а также пределы прочности
, а также пределы прочности![]() . В процессе численного моделирования были рассчитаны зависимости эффективных характеристик от концентрации стеклянной компоненты микросфер, эти зависимости показаны на рисунках 2-5. В процессе численного моделирования были рассчитаны зависимости эффективных характеристик от концентрации стеклянной компоненты микросфер, эти зависимости показаны на рисунках 2-5. Графики зависимости модуля упругости и коэффициента теплопроводности от коэффициента армирования являются монотонными, как это и следует из теоретических соображений [3]. Коэффициент Пуассона
. В процессе численного моделирования были рассчитаны зависимости эффективных характеристик от концентрации стеклянной компоненты микросфер, эти зависимости показаны на рисунках 2-5. В процессе численного моделирования были рассчитаны зависимости эффективных характеристик от концентрации стеклянной компоненты микросфер, эти зависимости показаны на рисунках 2-5. Графики зависимости модуля упругости и коэффициента теплопроводности от коэффициента армирования являются монотонными, как это и следует из теоретических соображений [3]. Коэффициент Пуассона ![]() композита меняется немонотонным образом – до значения концентрации
композита меняется немонотонным образом – до значения концентрации ![]() он уменьшается, а затем снова возрастает, однако эти изменения невелики по абсолютной величине (от 0.35 до 0.337), вцелом, значения коэффициента Пуассона композита близки по своим значениям к коэффициенту Пуассона матрицы. График зависимости прочности на растяжение
он уменьшается, а затем снова возрастает, однако эти изменения невелики по абсолютной величине (от 0.35 до 0.337), вцелом, значения коэффициента Пуассона композита близки по своим значениям к коэффициенту Пуассона матрицы. График зависимости прочности на растяжение ![]() не является монотонным: при увеличении концентрации микросфер прочность композита вначале резко падает почти в 2 раза по сравнению с прочностью неармированной матрицы, далее при увеличении содержания микросфер она немного возрастает (примерно на 15%), а затем при предельном содержании микросфер – снова падает. Небольшие осцилляции прочности, показанные на рисунке 5, обусловлены численной погрешностью вычислений прочности, которая вызвана сеточными эффектами (при различных концентрациях микросфер конечно-элементная сетка была различной и это вносило определенную погрешность в результат расчета прочности).
не является монотонным: при увеличении концентрации микросфер прочность композита вначале резко падает почти в 2 раза по сравнению с прочностью неармированной матрицы, далее при увеличении содержания микросфер она немного возрастает (примерно на 15%), а затем при предельном содержании микросфер – снова падает. Небольшие осцилляции прочности, показанные на рисунке 5, обусловлены численной погрешностью вычислений прочности, которая вызвана сеточными эффектами (при различных концентрациях микросфер конечно-элементная сетка была различной и это вносило определенную погрешность в результат расчета прочности).
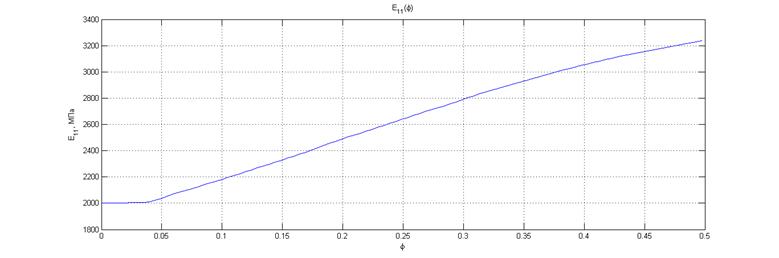
Рисунок 2. Зависимость эффективного модуля упругости ![]() дисперсно-армированного композита от концентрации микросфер
дисперсно-армированного композита от концентрации микросфер ![]() .
.
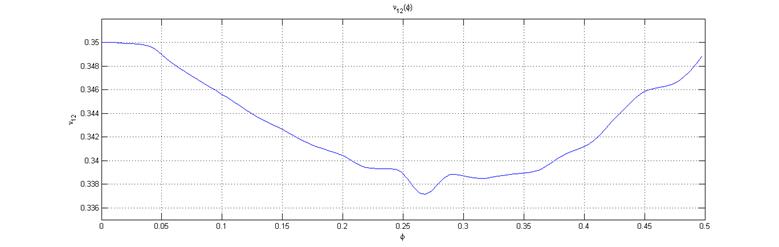
Рис. 3. Зависимость эффективного коэффициента Пуассона дисперсно-армированного композита от концентрации микросфер ![]() .
.

Рис. 4. Зависимость эффективного коэффициента теплопроводности ![]() дисперсно-армированного композита от концентрации микросфер
дисперсно-армированного композита от концентрации микросфер
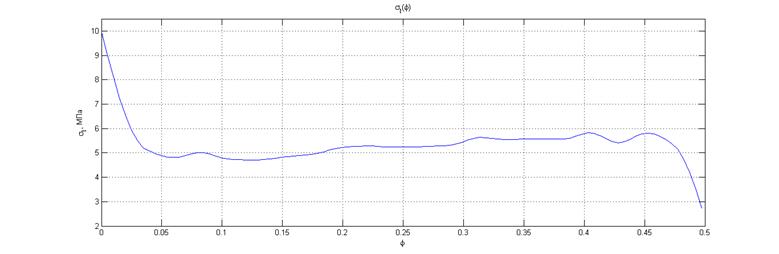
Рис. 5. Зависимость прочности на растяжение ![]() дисперсно-армированного композита от концентрации микросфер
дисперсно-армированного композита от концентрации микросфер
Для задачи оптимизации были выбраны следующие ограничения (2): ![]() и
и ![]() .
.
При этом значение оптимума было достигнуто при концентрации стеклянной фазы ![]() , что соответствует концентрации микросфер
, что соответствует концентрации микросфер ![]() . Соответствующее оптимальное значение плотности композита составляет
. Соответствующее оптимальное значение плотности композита составляет ![]() .
.
Выводы. Разработан численный метод решения задачи оптимизации микроструктуры композиционного материала, с одновременными ограничениями на теплофизические и механические характеристики. Метод основан на конечно-элементном расчете эффективных характеристик композита: модулей упругости, коэффициентов теплопроводности и прочностей, а также на итерационном решении задач оптимизации функционала плотности. Предложенный метод реализован на примере дисперсно-армированного композиционного материала с наполнителем в виде стеклянных микросфер. Численно рассчитаны зависимости эффективных характеристик композита от коэффициента армирования, а также найдено оптимальное содержание наполнителя композита. Предложенный метод может использоваться для определения оптимальных структур композитов в задачах проектирования тепловой защиты.
Исследование выполнено при поддержке Министерства образования и науки Российской Федерации (Соглашения №14.B37.21.0448, 14.B37.21.1869, государственные контракты №14.514.11.4052, 14.516.11.0083, НИР № 1.5433.2011), грантов Президента РФ (МК-6421-2012-9, МК-765.2012.8, МК-6573.2013.3) и гранта РФФИ №12-08-00998.
Список литературы
1. Yu.I. Dimitrienko, G.A. Efremov, S.A. Chernyavsky. Optimum design of erosion-stable heatshield composite materials // Applied Composite Materials. 1997. № 4. 35-52.
2. Бахвалов Н.С., Панасенко Г.П. Осреднение процессов в периодических средах. М.: Наука, 1984. 352 с.
3. Победря Б.Е. Механика композиционных материалов. М.: МГУ, 1984. 336 с.
4. Санчес-Паленсия Э. Неоднородные среды и теория колебаний: пер. с англ. М.: Мир, 1984. 336 с.
5. Димитриенко Ю.И., Соколов А.П. Разработка автоматизированной технологии вычисления эффективных упругих характеристик композитов методом асимптотического осреднения // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2008. № 2. С. 57-67.
6. Димитриенко Ю.И., Соколов А.П. Автоматизация прогнозирования свойств композиционных материалов на основе метода асимптотического осреднения // Информационные технологии. 2008. № 8. С. 31-38.
7. Димитриенко Ю.И., Кашкаров А.И. Конечно-элементный метод для вычисления эффективных характеристик пространственно-армированных композитов // Вестник МГТУ им. Баумана. Сер. Естественные науки. 2002. № 2. С. 95-108.
8. Димитриенко Ю.И., Соколов А.П., Шпакова Ю.В., Юрин Ю.В. Моделирование поверхностей прочности композитов на основе микроструктурного конечно-элементного анализа // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012. № 11. DOI: http://dx.doi.org/10.7463/1112.0496336.
9. Димитриенко Ю.И., Соколов А.П. Многомасштабное моделирование упругих композиционных материалов// Математическое моделирование.- 2012. – Т. 24. – № 5. – С. 3-20.
10. Димитриенко Ю.И., Соколов А.П. Современный численный анализ механических свойств композиционных материалов // Известия РАН. Физическая серия – Т. 75, № 11. - 2011. – с. 1551-1556.
11. Димитриенко Ю.И., Морозов А.Н., Соколов А.П., Ничеговский Е.С. Моделирование эффективных пьезоэлектроупругих свойств композиционных материалов// Вестник МГТУ им.Н.Э. Баумана. Сер. Естественные науки.-№ 3. -2010.- с. 86-97.
12. Димитриенко Ю.И., Ничеговский Е.С. Численное моделирование магнитных свойств композиционных материалов// Вестник МГТУ им.Н.Э. Баумана. Сер. Естественные науки.-№ 1. -2010.- с. 3-12.
13. Димитриенко Ю.И. Основы механики твердого тела/ Механика сплошной среды.Т.4.-Изд-во МГТУ им.Н.Э. Баумана.-2013.-580 с.
14. Ю.И. Димитриенко, А.П. Соколов, С.В. Сборщиков Моделирование микро-разрушения тканевых композитов// Вестник МГТУ им.Н.Э. Баумана. Сер. Естественные науки. Спец.выпуск № 3 «Математическое моделирование».-2012.-с. 5-19.
15. Лебедев А.А. Развитие теорий прочности в механике материалов // Проблемы прочности. 2010. № 5. С. 127-146.
16. Банди Б. Методы оптимизации. Вводный курс. М.: Радио и связь, 1988.
Публикации с ключевыми словами: прочность, упругость, композиционные материалы, МКЭ, методы оптимизации, оптимальное проектирование, теплопроводность, метод асимптотического осреднения, микросферы
Публикации со словами: прочность, упругость, композиционные материалы, МКЭ, методы оптимизации, оптимальное проектирование, теплопроводность, метод асимптотического осреднения, микросферы
Смотри также:
- Оптимизация многокомпонентных дисперсно-армированных композитов на основе сплайн-аппроксимации
- Математическое моделирование диэлектрических свойств полимер-керамических композиционных материалов методом асимптотического осреднения
- Применение метода конечных элементов с переменными матрицами для моделирования динамики движения конструкций стартовых комплексов
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



