научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2013
DOI: 10.7463/1113.0620593
УДК 621.455.4
Россия, МГТУ им. Н.Э. Баумана
Введение
Одним из наиболее распространенных классов электроракетных двигателей являются холловские двигатели. В основе принципа их работы лежит генерация и ускорение ионов рабочего вещества в кольцевом канале, в котором горит разряд в скрещенных электрическом и магнитном полях. Такая схема используется во многих газоразрядных устройствах, применяемых как для космических, так и для наземных целей, в том числе для технологических устройств.
Для анализа рабочих процессов в двигателях с анодным слоем за полувековую историю их разработки были создано много математических моделей [1-3]. Все разработанные модели ставили целью определить распределение локальных параметров плазмы в разрядном промежутке. Такого рода были массивными и имели большое количество допущений и коэффициентов, которые необходимо было получить экспериментально. Быстрые расчеты по таким моделям были весьма затруднительными. Однако для проектирования двигателей с анодным слоем необходимо знать небольшое количество параметров. Самым важным среди них является распределение потенциала, а также расположение анодного слоя. В данной работе предпринята попытка сделать простую модель, учитывающую реальные геометрические размеры двигателя и распределение магнитного поля, которая позволяет быстро оценить распределение потенциала плазмы и положение внешней, низковольтной границы анодного слоя.
В работах [4-6] был предложен параметр, характеризующий распределение магнитного поля в канале двигателя, который был назван удельным магнитным потоком Ω(х), Тл·м. Удельный магнитный поток численно равен интегралу от радиальной составляющей индукции магнитного поля Bz(x) вдоль оси ускорительного канала от точки х до бесконечности:
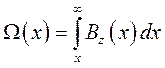 , (1)
, (1)
Эта величина использовалась в работах [1-3] для подсчета угла азимутального отклонения ионов в магнитном поле ускорительного канала. В данной работе показано, что этот параметр можно использовать для нахождения распределения потенциала плазмы в ускорительном канале холловского двигателя.
Постановка задачи
Введем исходные геометрические величины, характеризующие ускорительный канал холловского двигателя: средний диаметр канала D, м; ширина ∆, м. Величину радиальной составляющей индукции магнитного поля Bz(x) будем считать неизменной по азимуту. Распределение удельного магнитного потока обозначим как Ω(х), Тл·м. Напряжение разряда будем обозначать как U, В, массовый расход как ![]() , кг/с;
, кг/с;
Примем следующие допущения:
— нестационарные процессы, осцилляции и т.д. пренебрежимо малы;
— распределение параметров плазмы неизменно по азимуту канала;
— в ускорительном канале соблюдается условие квазинейтральности;
— движение ионов в канале бесдисипативное, после рождения ион пролетает зону разряда без столкновений;
— образование ионов и электронов происходит ударной ионизацией из основного состояния;
— процессом ступенчатой ионизации, теплопроводностью и излучением плазмы пренебрегаем;
— в канале образуются только однократно ионизованные ионы;
— распределение электронов по энергиям в ускоряющем слое является максвелловским с температурой Те;
— кулоновские столкновения в ускорительном канале отсутствуют;
— температура электронов много больше температуры ионов.
Энергию электронов εeбудем выражать в электрон-вольтах:
 (2)
(2)
В работе [1] показано, что для рассматриваемых условий работы отношение частоты ионизации ni(εe) к частоте упругих столкновений электронов ne(εe) постоянно:
 (3)
(3)
Коэффициент δ для инертных газов примем равным 3, для всех металлов, кроме щелочных – 5, для щелочных металлов – 20 [1].
Если стенки канала не оказывают заметного влияния на локальную температуру электронов Te(x), то, по экспериментальным данным, она определяется электрическим потенциалом плазмы φ(x) [1] и для средней энергии электронов мы можем записать:
![]() , (4)
, (4)
где, a – безразмерный коэффициент пропорциональности.
Модель расчета распределения потенциала плазмы в ускорительном канале холловского двигателя
Воспользуемся уравнением движения для электронной компоненты без учета инерционной составляющей [1]:
 , (5)
, (5)
где, ne – частота упругих столкновений электронов, Ve – скорость электронов, E – напряженность электрического поля, B – индукция магнитного поля, ![]() – градиент электронного давления, ne– концентрация электронов.
– градиент электронного давления, ne– концентрация электронов.
Выберем прямоугольную систему координат, с началом на низковольтной границе анодного слоя и осью Ох, направленной к высоковольтной границе, а также осью Оz. направленной поперек канала (рис. 1). Распределение удельного магнитного потока в канале будет определяться следующими величинами:
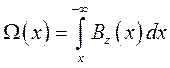 ,
, 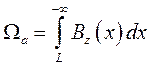 ,
,  , (6)
, (6)
Где Ω(х) – распределение удельного магнитного потока в разрядном промежутке, Ωa – удельный магнитный поток на аноде, Ωk – удельный магнитный поток на низковольтной границе (на катоде).

Рис. 1. Схема распределения расчетных параметров вдоль канала:
je(x) – распределение плотности тока электронов, Ω(x) – распределение удельного магнитного потока, f(x) – распределение потенциала электрического поля, U – напряжение разряда, Ωa – удельный магнитный поток у анода, Ωk – удельный магнитный поток на низковольтной границе, E – напряженность электрического поля, В – индукция магнитного поля
Запишем уравнение (4) в проекциях на ось Ох с учетом того, что индукция магнитного поля имеет лишь радиальную составляющую Bz(x), а напряженность электрического поля Ex(x) – только осевую, причем градиент электронного давления пренебрежимо мал [7] и выделим в левую часть скорость дрейфа электронной компоненты поперек магнитного поля Vex(x):
 ,
,  (7)
(7)
где βe (х) – параметр Холла для электронов.
При условии ![]() из (7) получаем выражение для плотности сквозного электронного тока:
из (7) получаем выражение для плотности сквозного электронного тока:
 (8)
(8)
Изменение плотности электронного тока в направлении анода je(х) определяется ионизационными процессами и зависит от концентрации плазмы ne(х) и частоты ионизации ni(х):
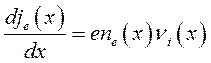 (9)
(9)
Из (8) выделяем ne(х) и подставляем в (8) с учетом (3) получаем:
 (10)
(10)
Удельная объемная мощность, поглощаемая электронной компонентой в слое dx, равна мощности оммического тепловыделения в этом слое за вычетом затрат на ионизацию Qi(x) и потерь на стенках канала Qw(x):
![]() (11)
(11)
Энергетические затраты на ионизацию можно определить, используя константу Столетова:
![]() (12)
(12)
где I – потенциал ионизации, эВ.
Если стенки канала находятся под катодным потенциалом, то потери мощности Qw(x) в уравнении (11) можно не учитывать [1].
Тогда, раскрывая дифференциал в левой части выражения (11), получаем:
 (13)
(13)
Подставляя в левую часть (13) выражение (4) и в последний член правой части (13) выражение (9), преобразуем полученное выражение:
 (14)
(14)
Подставляем (10) в левую часть (14) и сокращая на je(х) получаем:
 (15)
(15)
Откуда:
 (16)
(16)
Интегрируем полученное уравнение при начальных условиях x=0; j(x)=0; W(0)=Wk и получаем выражение для распределения электрического потенциала в ускорительном канале:
 (17)
(17)
Из (17) находим удельный магнитный поток на низковольтной границе из условия x=L; j(L)=U; W(L)=Wa:
 (18)
(18)
Зная распределение магнитного поля в ускорительном канале из (18) можно найти положение низковольтной границы.
Пример расчета
Приведем пример расчета распределения потенциала плазмы. Допустим, что распределение индукции магнитного поля вдоль ускорительного канала носит экспоненциальный характер (рис. 2), рабочее вещество – ксенон, напряжение разряда – 1000 В и 1500 В. На рисунке 3 показаны распределения удельного магнитного потока, посчитанные по выражению (1), а также указаны значения удельного магнитного потока на аноде и рассчитанные по выражению (17) значения удельного магнитного потока на низковольтной границе, рассчитанные по выражению (18). В таблице 1 приведены значения исходных и расчетных параметров для обоих расчетов. Распределение потенциала, рассчитанное для обоих случаев, показано на рисунке 4.
Таблица 1. Результаты расчета
Параметры | № 1 | № 2 |
Рабочее вещество | Ксенон | Ксенон |
Потенциал ионизации, I, эВ | 12,13 | 12,13 |
Параметр δ | 3 | 3 |
Напряжение, U, В | 1000 | 1500 |
Параметр a | 0,5 | 0,5 |
Удельный магнитный поток на аноде, Ωa, Тл.м | 6,7×10-4 | 5,2×10-4 |
Удельный магнитный поток на низковольтной границе, Ωk, Тл.м | 4,7×10-4 | 2,6×10-4 |

Рис. 2. Распределения индукции магнитного поля в канале, используемое в расчете.

Рис. 3. Распределение удельного магнитного потока.

Рис. 4. Распределение потенциала плазмы. № 1 – 1000 В, № 2 – 1500 В.
Выводы
Расчеты показывают, что при заданном распределении магнитного поля, характерном для двигателя с анодным слоем, положение низковольтной границы соответствует практическому опыту [8, 9]. Таким образом, можно сделать вывод, что полученные соотношения позволяют быстро оценить распределение электрического потенциала в ускорительном канале двигателя с анодным слоем, а также найти положение низковольтной границы разряда.
Благодарность
Работа была выполнена при поддержке Гранта № 14.132.21.1587 Министерства образования и науки Российской Федерации.
Список литературы
1. Гришин С.Д., Лесков Л.В. Электрические ракетные двигатели. М.: Машиностроение, 1989. 216 с.
2. Морозов А.И. Физические основы космических электрореактивных двигателей. М.: Атомиздат, 1978. 328 с.
3. Калашников В.К., Саночкин Ю.В. Разряд в ускорителе с замкнутым E┴H-дрейфом изотермических электронов // Физика плазмы. 1981. Т. 7, вып. 2. С. 303-311.
4. Духопельников Д.В., Ивахненко С.Г. Влияние азимутального отклонения ионов на форму пучка двигателя с анодным слоем // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012. № 10. DOI: 10.7463/1012.0483832
5. Марахтанов М.К., Духопельников Д.В., Ивахненко С.Г., Воробьев Е В., Крылов В.И. Влияние азимутального отклонения ионов плазменной струи на тяговый КПД двигателя с анодным слоем // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012. № 12. DOI: 10.7463/1212.0483944
6. Марахтанов М.К., Духопельников Д.В., Ивахненко С.Г., Воробьев Е.В. Экспериментальное подтверждение эффекта азимутального отклонения ионов в двигателях с анодным слоем // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2012. № 11. DOI: 10.7463/1112.0483882
7. Архипов А.С., Ким В.П., Сидоренко Е.К. Стационарные плазменные двигатели Морозова. М.: Изд-во МАИ, 2012. 292 с.
8. Алексеев Д.Н. Исследование особенностей рабочего процесса и ресурса работы ускорителя с замкнутым дрейфом электронов при низких ускоряющих напряжениях: дис. ... канд. техн. наук. М., МГТУ им. Баумана, 1993. 136 с.
9. Хохлов Ю.А. Плазменные ускорители с азимутальным дрейфом электронов для получения тонких оптических пленок: дис. ... канд. техн. наук. М., МГТУ им. Баумана, 1987. 254 с.
Публикации с ключевыми словами: двигатель с анодным слоем, удельный магнитный поток, потенциал плазмы
Публикации со словами: двигатель с анодным слоем, удельный магнитный поток, потенциал плазмы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



