научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2013
DOI: 10.7463/1113.0619595
Россия, МГТУ им. Н.Э. Баумана
Основная идея ко-эволюционных алгоритмов (ко-алгоритмов) оптимизации состоит в следующем. Одновременно в пространстве поиска задачи оптимизации эволюционируют несколько субпопуляций, каждая из которых решает исходную оптимизационную задачу и имеет свою стратегию оптимизации, которая определяется значениями свободных параметров субалгоритма (алгоритма, который управляет данной субпопуляцией). В процессе решения задачи субпопуляции конкурируют между собой за некоторый ресурс (в данной работе – число вычислений значений оптимизируемой функции), который в процессе работы ко-алгоритма перераспределяется в пользу более эффективной из них [1].
Целью ко-гибридизации алгоритмов поисковой оптимизации является повышение их эффективности, которое достигается тем, что в процессе ко-эволюции, по сути, решается задача мета-оптимизации этих алгоритмов – то есть задача определения значений их свободных параметров, которые являются наилучшими для данной задачи оптимизации [2].
Чаще всего при ко-гибридизации в качестве субалгоритмов используют генетический алгоритм и его модификации [3]. Помимо большого числа достоинств генетический алгоритм обладает и рядом недостатков. Так, индивиды в популяции генетического алгоритма не имеют памяти и, по-сути, не «сотрудничают» между собой. В отличие от этого, в используемом нами для ко-гибридизации популяционном алгоритме роя частиц (ParticleSwarmOptimization, PSO) агенты (частицы) «помнят» свое лучшее положение за всю предысторию поиска. Кроме того, в алгоритме PSOинформация о лучшем из найденных роем решении раньше или позже становится известной всем частицам, то есть в этом алгоритме имеет место «сотрудничество» между частицами.
Данная статья является продолжением работы [1], в которой предложен двухпопуляционный ко-алгоритма Co-PSO, построенный на основе алгоритмов PSO, использующих топологии соседства «клика» и «кольцо».
Целью работы является разработка многопопуляционного ко-алгоритма PSO, программная реализация этого алгоритма, исследование эффективности разработанного алгоритмического и программного обеспечения.
В первом разделе работы приводим постановку задачи глобальной оптимизации и схему базового алгоритма PSO. Во втором разделе представляем разработанный нами ко-алгоритм Co-PSOи MatLab-программное обеспечение, реализующее этот алгоритм. Третий раздел посвящен исследованию эффективности разработанного алгоритмического и программного обеспечения. В четвертом разделе рассматриваем решение с помощью разработанных средств задачи оптимального управления космическим аппаратом на этапе его спуска в атмосфере Земли. В заключении сформулированы основные результаты работы и очерчены перспективы ее развития.
1. Постановка задачи глобальной оптимизации и схема алгоритма роя частиц для ее решения
Рассматриваем детерминированную непрерывную задачу глобальной условной минимизации
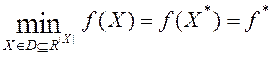 , (1)
, (1)
где ![]() – скалярная целевая функция (критерий оптимальности),
– скалярная целевая функция (критерий оптимальности), ![]() – искомое минимальное значение целевой функции,
– искомое минимальное значение целевой функции, ![]() –
– ![]() -мерный вектор варьируемых параметров,
-мерный вектор варьируемых параметров, ![]() – множество допустимых значений этого вектора (область поиска);
– множество допустимых значений этого вектора (область поиска); ![]() –
– ![]() -мерное арифметическое пространство.
-мерное арифметическое пространство.
Множество частиц в рое обозначаем ![]() , где
, где ![]() – число частиц (размер популяции). На итерации tкоординаты частицы
– число частиц (размер популяции). На итерации tкоординаты частицы ![]() определяют
определяют ![]() -мерные векторы ее координат
-мерные векторы ее координат ![]() и «скорости»
и «скорости» ![]() . Начальные координаты и «скорости» всех частиц роя полагаем заданными и равными
. Начальные координаты и «скорости» всех частиц роя полагаем заданными и равными ![]() ,
, ![]() соответственно.
соответственно.
Основные итерационные формулы алгоритма PSOимеют вид
![]() , (2)
, (2)
![]() . (3)
. (3)
Здесь ![]() -
- ![]() -мерный вектор псевдослучайных чисел, равномерно распределенных в интервале
-мерный вектор псевдослучайных чисел, равномерно распределенных в интервале ![]() ;
; ![]() - символ покомпонентного умножения векторов;
- символ покомпонентного умножения векторов; ![]() - вектор координат частицы
- вектор координат частицы ![]() с наилучшим (в смысле формулы (1)) значением целевой функции
с наилучшим (в смысле формулы (1)) значением целевой функции ![]() за все время поиска
за все время поиска ![]() ;
; ![]() - вектор координат соседней с данной частицы с наилучшим за то же время значением целевой функции;
- вектор координат соседней с данной частицы с наилучшим за то же время значением целевой функции; ![]() ,
, ![]() ,
, ![]() - свободные параметры алгоритма. Параметр
- свободные параметры алгоритма. Параметр ![]() определяет «инерционные» свойства частицы,
определяет «инерционные» свойства частицы, ![]() – ее «когнитивные» свойства,
– ее «когнитивные» свойства, ![]() – «социальность» частицы. Рекомендуемые значения параметров
– «социальность» частицы. Рекомендуемые значения параметров ![]() ,
, ![]() ,
, ![]() равны, соответственно, 0,7298; 1,49618; 1,49618 [4].
равны, соответственно, 0,7298; 1,49618; 1,49618 [4].
Соседство частиц в рое определяет их топология соседства, задаваемая неориентированным графом, в котором вершины графа соответствуют частицам роя, а ребра связывают непосредственных соседей. В алгоритме PSO обычно используют топологии
‑ «клика» (глобально оптимальная топология),
‑ «кольцо» (локально оптимальная топология),
‑ «двумерный тор» (топология фон Неймана),
‑ «кластер».
Топологии «клика» соответствует полносвязный граф, в котором соседями каждой из частиц ![]() являются остальные
являются остальные ![]() частицы. Диаметр клики равен единице. В топологии «кольцо» соседями каждой из частиц являются всего две частицы, которые имеют соседние номера. Диаметр соответствующего графа равен
частицы. Диаметр клики равен единице. В топологии «кольцо» соседями каждой из частиц являются всего две частицы, которые имеют соседние номера. Диаметр соответствующего графа равен 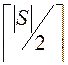 , где
, где ![]() ‑ символ ближайшего целого большего.
‑ символ ближайшего целого большего.
Обзор большого числа модификаций алгоритма PSOпредставлен в работе [4].
2. Ко-алгоритм Co-PSO и его программная реализация
2.1. Схема ко-алгоритма Co-PSO
Поскольку речь идет о ко-алгоритмической гибридизации алгоритмов PSO, ко-эволюционирующие субпопуляции далее называем суброями. Суброи обозначаем ![]() , где
, где ![]() ‑ их число. Схема предлагаемого ко-алгоритма Co-PSOимеет следующий вид.
‑ их число. Схема предлагаемого ко-алгоритма Co-PSOимеет следующий вид.
1) Задаем числа суброев, топологии соседства, используемые каждым из суброев, значения свободных параметров субалгоритмов.
2) Задаем значения свободных параметров ко-алгоритма:
‑ величина ресурса ![]() – максимально допустимое число испытаний (вычислений значений целевой функции);
– максимально допустимое число испытаний (вычислений значений целевой функции);
‑ интервал адаптации ![]() ;
;
- величина штрафа ![]() ;
;
‑ минимально допустимый размер суброя ![]() или его относительное значение
или его относительное значение
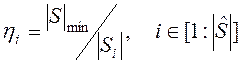 .
.
3) Инициализируем суброи, то есть, присваиваем всем частицам каждого из суброев ![]() начальные положения в пространстве поиска и начальные «скорости».
начальные положения в пространстве поиска и начальные «скорости».
3) Реализуем асинхронное выполнение каждым суброем ![]() независимых итераций.
независимых итераций.
4) Производим оценку эффективности суброев.
5) Проверяем выполнение условия останова. В случае выполнения этого условия, в качестве решения принимаем лучшее решение, найденное роем, и прекращаем вычисления.
6) Осуществляем перераспределение ресурса.
7) Реализуем миграцию лучших частиц. Частицы всех суброев объединяем в единый массив и сортируем в порядке убывания соответствующих значений целевой функции. Затем каждому из суброев из этого массива передаем число частиц, пропорциональное текущему размеру суброя.
8) Переходим к шагу 3.
Оценку эффективности суброя ![]() производим на основе вычисления текущих значений его функции пригодности
производим на основе вычисления текущих значений его функции пригодности ![]() , где
, где ![]() ‑ номер текущей итерации;
‑ номер текущей итерации; ![]() ‑ общее число итераций. Пригодность суброя есть мера его адаптации (приспособленности) к решаемой задаче оптимизации. Значение пригодности вычисляем по формуле
‑ общее число итераций. Пригодность суброя есть мера его адаптации (приспособленности) к решаемой задаче оптимизации. Значение пригодности вычисляем по формуле
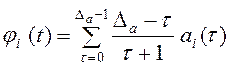 ,
, ![]() , (4)
, (4)
где ![]() , если суброй
, если суброй ![]() на итерации
на итерации ![]() включал в себя лучшую во всей популяции частицу, и
включал в себя лучшую во всей популяции частицу, и ![]() в противном случае. Заметим, что вес величины
в противном случае. Заметим, что вес величины ![]() определяется отношением
определяется отношением 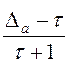 , так что при
, так что при ![]() (текущая итерация) этот вес максимален и равен интервалу адаптации
(текущая итерация) этот вес максимален и равен интервалу адаптации ![]() . С уменьшение номера итерации
. С уменьшение номера итерации ![]() вес величины
вес величины ![]() в сумме (4) быстро уменьшается [1].
в сумме (4) быстро уменьшается [1].
Перераспределение ресурса производим на основе приспособленности суброев (4). Если текущее значение пригодности суброя ![]() максимально по сравнению с пригодностями остальных суброев, то этот суброй признаем победившим, а остальные суброи – проигравшими. Перераспределение ресурса осуществляем путем сокращения размера каждого из проигравших суброев на величину штрафа, определяемого величиной
максимально по сравнению с пригодностями остальных суброев, то этот суброй признаем победившим, а остальные суброи – проигравшими. Перераспределение ресурса осуществляем путем сокращения размера каждого из проигравших суброев на величину штрафа, определяемого величиной ![]() , и увеличения размера победившего суброя на число, равное сумме потерь проигравших. Таким образом, общий размер роя не меняется [1].
, и увеличения размера победившего суброя на число, равное сумме потерь проигравших. Таким образом, общий размер роя не меняется [1].
Если размер проигравшего суброя оказывается меньше величины ![]() , то принимаем его равным этой величине. Таким образом, если
, то принимаем его равным этой величине. Таким образом, если ![]() – размер суброя
– размер суброя ![]() , проигравшего на текущем интервале адаптации, то на следующем интервале размер этого суброя будет равен величине
, проигравшего на текущем интервале адаптации, то на следующем интервале размер этого суброя будет равен величине
![]()
![]() .
.
Если же суброй ![]() выиграл на текущем интервале адаптации, то на следующем интервале его размер определяет выражение
выиграл на текущем интервале адаптации, то на следующем интервале его размер определяет выражение
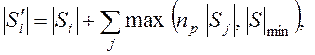
![]() ,
, ![]() .
.
2.2. Обзор других методов ко-гибридизации алгоритмов PSO
Отметим следующее обстоятельство. Задача глобальной оптимизации (1) поставлена нами как задача условной оптимизации. Однако канонический алгоритм PSOи рассмотренная выше схема ко-алгоритма PSOне учитывают ограничений на вектор варьируемых параметров ![]() , то есть, ориентированы на решение задачи безусловной оптимизации. Мы полагаем, что задача условной оптимизации (1) сведена к задаче безусловной оптимизации методом штрафных функций (п. 4).
, то есть, ориентированы на решение задачи безусловной оптимизации. Мы полагаем, что задача условной оптимизации (1) сведена к задаче безусловной оптимизации методом штрафных функций (п. 4).
Известно большое число приемов, позволяющих учитывать в популяционных алгоритмах оптимизации и, в частности, в алгоритме PSO, ограничения на компоненты вектора ![]() . Такие приемы, по сути, модифицируют базовые популяционные алгоритмы и приводят к новым алгоритмам. В ко-алгоритмах ограничения на вектор
. Такие приемы, по сути, модифицируют базовые популяционные алгоритмы и приводят к новым алгоритмам. В ко-алгоритмах ограничения на вектор ![]() могут быть учтены также на уровне ко-алгоритма. Приведем несколько примеров.
могут быть учтены также на уровне ко-алгоритма. Приведем несколько примеров.
В работе [5] предложен ко-алгоритм CPSO(Co-evolutionaryPSO) для случая, когда множество допустимых значений вектора варьируемых параметров ![]() определяют ограничения типа неравенств
определяют ограничения типа неравенств ![]() . Алгоритм CPSO использует мультирой
. Алгоритм CPSO использует мультирой ![]() , содержащий
, содержащий ![]() роев по
роев по ![]() частиц в каждом, а также рой
частиц в каждом, а также рой ![]() , число частиц в котором равно числу ограничивающих функций
, число частиц в котором равно числу ограничивающих функций ![]() . Размерность вектора параметров, ассоциированного с каждой из частиц роев
. Размерность вектора параметров, ассоциированного с каждой из частиц роев ![]() , равна
, равна ![]() . В рое
. В рое ![]() размерность того же вектора равна числу штрафных коэффициентов в штрафной функции, с помощью которой задача условной оптимизации сведена к задаче безусловной оптимизации. Рои
размерность того же вектора равна числу штрафных коэффициентов в штрафной функции, с помощью которой задача условной оптимизации сведена к задаче безусловной оптимизации. Рои ![]() используются для ко-алгоритмического поиска решения указанной задачи безусловной оптимизации, а рой
используются для ко-алгоритмического поиска решения указанной задачи безусловной оптимизации, а рой ![]() ‑ для такого же поиска оптимальных значений коэффициентов штрафа.
‑ для такого же поиска оптимальных значений коэффициентов штрафа.
Близкий подход к решению задачи условной оптимизации используется в работе [6], в которой наряду с ограничениями типа неравенств рассматриваются ограничения типа равенств вида ![]() . При выполнении условий теоремы Куна-Таккера из этой теоремы следует, что исходная задача минимизации (1) эквивалентна задаче безусловной минимизации соответствующей функции Лагранжа по вектору варьируемых параметров
. При выполнении условий теоремы Куна-Таккера из этой теоремы следует, что исходная задача минимизации (1) эквивалентна задаче безусловной минимизации соответствующей функции Лагранжа по вектору варьируемых параметров ![]() и такой же задаче максимизации этой функции по множителям Лагранжа. Для решения указанной минимаксной задачи используется два ко-эволюционирующих роя PSO
и такой же задаче максимизации этой функции по множителям Лагранжа. Для решения указанной минимаксной задачи используется два ко-эволюционирующих роя PSO![]() , их которых рой
, их которых рой ![]() решает задачу минимизации, а рой
решает задачу минимизации, а рой ![]() ‑ задачу максимизации.
‑ задачу максимизации.
Отличная от представленных выше схема ко-эволюционной гибридизации используется в работе [7]. Предложенный в этой работе алгоритм CECBPSO(Сo-EvolutionaryCulturalBasedParticleSwarmOptimization), основан на культурном алгоритме (Culturalalgorithm) [8].
2.3. Программная реализация ко-алгоритма Co-PSO
Программная реализация ко-алгоритма Co-PSOвыполнена в среде пакета программ MatLabR2012aи на языке программирования этого пакета. Язык программирования MatLabпредставляет собой высокоуровневый интерпретируемый язык, основанный на операциях с векторами и матрицами. Язык включает в себя широкий набор функций, объектно-ориентированные возможности и интерфейсы к программам, написанным на других языках программирования. MatLab-программы могут быть оформлены как функции и скрипты. Программная реализация ко-алгоритма PSOвыполнена в виде скриптов и также получила наименование Co-PSO.
Программа Co-PSOвключает в себя расширяемые библиотеки тестовых функций и графов, определяющих топологии соседства, которые могут быть использованы субалгоритмами PSO. В программе могут быть заданы различные условия окончания итераций, но во всех случаях их число ограничено заданным пользователем значением ![]() .
.
Для повышения вероятности локализации глобального экстремума целевой функции, программа Co-PSOподдерживает метод мультистарта. По результатам заданного пользователем числа стартов ![]() программа вычисляет оценку вероятности локализации глобального экстремума
программа вычисляет оценку вероятности локализации глобального экстремума ![]() , а также средние числа испытаний
, а также средние числа испытаний ![]() , итераций
, итераций ![]() и побед данного суброя
и побед данного суброя ![]() , а также предельные размеры суброев-победителей
, а также предельные размеры суброев-победителей ![]() ,
, ![]() , размер суброя-победителя в момент окончания итераций
, размер суброя-победителя в момент окончания итераций ![]() , величины свободных параметров
, величины свободных параметров ![]() суброя-победителя (если эти параметры были различны для различных суброев). Победителем считается тот из суброев, который обеспечил меньшее результирующее значение целевой функции.
суброя-победителя (если эти параметры были различны для различных суброев). Победителем считается тот из суброев, который обеспечил меньшее результирующее значение целевой функции.
В качестве результата работы программа Co-PSOможет построить график изменения значений целевой функции с ростом числа итераций для суброя-победителя а также графики изменения размеров суброев в функции номера итерации.
Всюду далее в данном разделе имеется в виду использование в качестве условия окончания итерационного процесса его стагнацию в течение ![]() итераций, когда лучшее достигнутое значение целевой функции изменяется на величину, не превышающую
итераций, когда лучшее достигнутое значение целевой функции изменяется на величину, не превышающую ![]() .
.
В качестве тестовых функций используем широко известные унимодальную овражную функцию Розенброка, четырехэкстремальную функцию Химмельблау и многоэкстремальную функцию Растригина. Для функций Розенброка и Растригина задача решается в параллелепипеде ![]() , где
, где ![]() , а для функции Химмельблау – в аналогичном параллелепипеде при
, а для функции Химмельблау – в аналогичном параллелепипеде при ![]() .
.
Во всех случаях вычислительный эксперимент выполнен для размерностей вектора варьируемых параметров ![]() , равных 2, 4, 8, 16, 32 и 64.
, равных 2, 4, 8, 16, 32 и 64.
Рассматриваем канонический алгоритм ![]() и два варианта ко-алгоритма PSO, называемые
и два варианта ко-алгоритма PSO, называемые ![]() ,
, ![]() и отличающиеся друг от друга используемыми субалгоритмами PSO.
и отличающиеся друг от друга используемыми субалгоритмами PSO.
Ко-алгоритм ![]() построен на основе шести суброев, из которых два имеют топологию «клика», два – «кольцо» и два – динамическую топологию. Значения свободных параметров
построен на основе шести суброев, из которых два имеют топологию «клика», два – «кольцо» и два – динамическую топологию. Значения свободных параметров ![]() всех субалгоритмов PSO постоянны и равны рекомендованным (п. 1).
всех субалгоритмов PSO постоянны и равны рекомендованным (п. 1).
Ко-алгоритм ![]() также построен на основе шести суброев, но все суброи в этом случае используют одну и ту же топологию соседства частиц. Значения свободных параметров
также построен на основе шести суброев, но все суброи в этом случае используют одну и ту же топологию соседства частиц. Значения свободных параметров ![]() указанных суброев случайным образом равномерно распределенные в интервале
указанных суброев случайным образом равномерно распределенные в интервале ![]() .
.
Свободные параметры ко-алгоритмов ![]() ,
, ![]() имеют следующие значения: интервал адаптации
имеют следующие значения: интервал адаптации ![]() ; величина штрафа
; величина штрафа ![]() ; минимально допустимый размер суброя
; минимально допустимый размер суброя ![]() . Число частиц в каждой из субпопуляций обоих ко-алгоритмов принято равным 50. Используем мультистарт с числом запусков
. Число частиц в каждой из субпопуляций обоих ко-алгоритмов принято равным 50. Используем мультистарт с числом запусков ![]() . Как и в предыдущем исследовании, в качестве тестовых используем функции Розенброка, Химмельблау, Растригина.
. Как и в предыдущем исследовании, в качестве тестовых используем функции Розенброка, Химмельблау, Растригина.
3.1. Канонический алгоритм PSO
Исследование эффективности канонического алгоритма PSO выполнено с целью тестирования разработанного алгоритмического и программного обеспечения, а также с целью создания базы для последующей сравнительной оценки эффективности ко-алгоритма Co-PSO. Рассмотрен канонический алгоритм PSO с топологиями соседства «клика», «кольцо» и динамическая топология (когда, начиная с топологии «кольцо», через каждое фиксированное число итераций в граф соседства случайным образом добавляется одно ребро). В качестве значений свободных параметров алгоритма использованы их рекомендованные значения (п. 1). Число частиц в популяции принято равным ![]() . Используем мультистарт с числом запусков алгоритма
. Используем мультистарт с числом запусков алгоритма ![]() .
.
Оценки вероятности ![]() локализации глобального экстремума в функции величины
локализации глобального экстремума в функции величины ![]() представлены в таблице 1. Аналогичная таблица 2 представляет средние числа испытаний
представлены в таблице 1. Аналогичная таблица 2 представляет средние числа испытаний ![]() .
.
Таблица 1 ‑ Оценки вероятности ![]() локализации глобального экстремума
локализации глобального экстремума
Тестовая функция |
Топология | Размерность вектора | |||||
2 | 4 | 8 | 16 | 32 | 64 | ||
Розенброка | клика | 100 | 93 | 90 | 80 | 67 | 64 |
кольцо | 80 | 73 | 60 | 53 | 50 | 43 | |
динамическая | 87 | 84 | 73 | 64 | 57 | 60 | |
Химмельблау | клика | 97 | 84 | 70 | 64 | 57 | 53 |
кольцо | 100 | 73 | 77 | 70 | 53 | 43 | |
динамическая | 93 | 80 | 73 | 64 | 50 | 40 | |
Растригина | клика | 77 | 67 | 60 | 53 | 47 | 32 |
кольцо | 100 | 93 | 87 | 77 | 70 | 64 | |
динамическая | 73 | 77 | 64 | 57 | 53 | 47 | |
Таблица 2 ‑ Оценки среднего числа испытаний ![]()
Тестовая функция |
Топология | Размерность вектора | |||||
2 | 4 | 8 | 16 | 32 | 64 | ||
Розенброка | клика | 3700 | 5150 | 12500 | 12650 | 14700 | 16400 |
кольцо | 9200 | 14750 | 16600 | 19500 | 21150 | 30700 | |
динамическая | 7600 | 11800 | 13200 | 16400 | 19750 | 28200 | |
Химмельблау | клика | 12100 | 14600 | 14000 | 17700 | 21400 | 27650 |
кольцо | 11700 | 14900 | 17250 | 16200 | 22700 | 25700 | |
динамическая | 10650 | 17700 | 22400 | 21600 | 25050 | 30250 | |
Растригина | клика | 6700 | 13000 | 15200 | 19100 | 25750 | 32900 |
кольцо | 5250 | 8200 | 14650 | 15750 | 21650 | 28200 | |
динамическая | 6400 | 10050 | 16350 | 22700 | 25300 | 30800 | |
Представленные в таблицах 1, 2 результаты подтверждают тот известный факт, что уменьшение диаметра графа соседства частиц ускоряет сходимость итерационного процесса, то есть повышает интенсивность поиска. С другой стороны, небольшой диаметр этого графа уменьшает широту поиска и повышает вероятность преждевременной сходимости итераций к локальному минимуму целевой функции. Таким образом, в каноническом алгоритме PSOтопологию соседства «кольцо» целесообразно использовать в случае многомерных многоэкстремальных целевых функций. При оптимизации более простых целевых функций лучшим решением может быть использование топологии типа «клика».
3.2. Ко-алгоритм Co-PSO![]()
Оценка вероятности локализации глобального экстремума. Зависимость величины ![]() от размерности вектора варьируемых параметров
от размерности вектора варьируемых параметров ![]() иллюстрирует рисунок 1, на котором одновременно показаны наиболее вероятные по мультистарту топологии суброев-победителей.
иллюстрирует рисунок 1, на котором одновременно показаны наиболее вероятные по мультистарту топологии суброев-победителей.
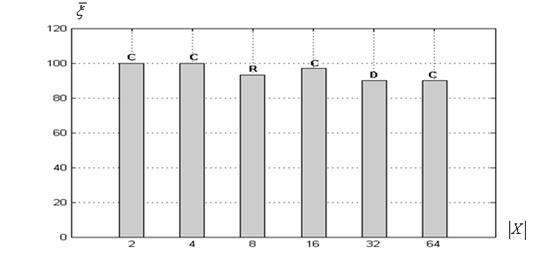
а) функция Розенброка
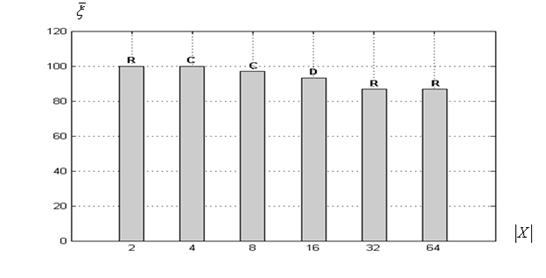
б) функция Химмельблау
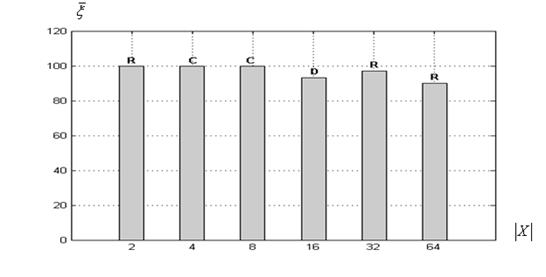
в) функция Растригина
Рисунок 1 – Оценка вероятности ![]() в функции величины
в функции величины ![]() : алгоритм
: алгоритм ![]() ; С – топология «клика», R – «кольцо», D –динамическая топология
; С – топология «клика», R – «кольцо», D –динамическая топология
Из рисунка 1а следует, что при низкой размерности вектора ![]() (равной 2, 4) для всех рассматриваемых тестовых функций алгоритм
(равной 2, 4) для всех рассматриваемых тестовых функций алгоритм ![]() обеспечивает 100% оценку вероятности локализации глобального минимума. В случае высокой размерности указанного вектора эта оценка не опускается ниже примерно 90% (при
обеспечивает 100% оценку вероятности локализации глобального минимума. В случае высокой размерности указанного вектора эта оценка не опускается ниже примерно 90% (при ![]() ). Важно, что величина
). Важно, что величина ![]() медленно уменьшается с ростом размерности вектора
медленно уменьшается с ростом размерности вектора ![]() . Сравнение рисунка 1 и таблицы 1 показывает, что во всех случаях алгоритм
. Сравнение рисунка 1 и таблицы 1 показывает, что во всех случаях алгоритм ![]() обеспечивает лучшую оценку вероятности
обеспечивает лучшую оценку вероятности ![]() , чем канонический алгоритм PSO.
, чем канонический алгоритм PSO.
Среднее число побед. На рисунке 2 приведены диаграммы зависимости среднего по ![]() стартам числа побед суброев
стартам числа побед суброев ![]() от величины
от величины ![]() для каждой из рассматриваемых топологий соседства.
для каждой из рассматриваемых топологий соседства.
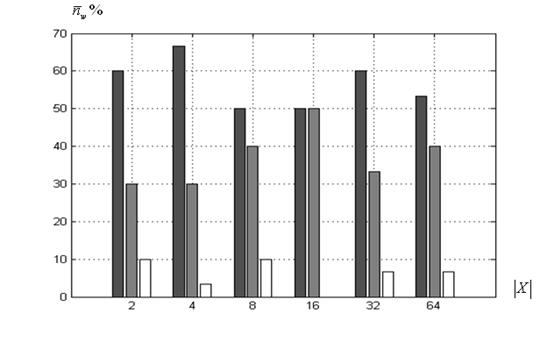
а) функция Розенброка
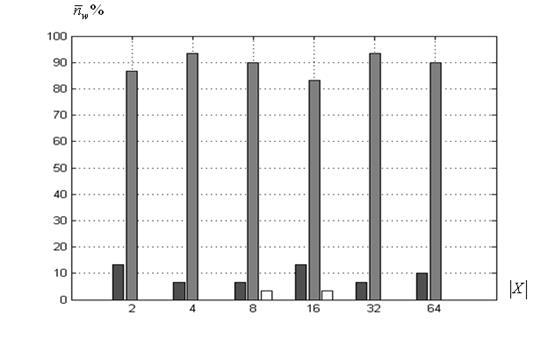
б) функция Химмельблау
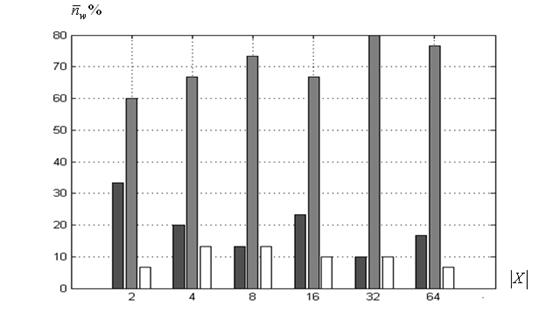
в) функция Растригина
Рисунок 2 – Среднее число побед ![]() в функции величины
в функции величины ![]() : ко-алгоритм
: ко-алгоритм ![]() ; ■ ‑ топология «клика»,■ ‑ «кольцо», □ ‑ динамическая
; ■ ‑ топология «клика»,■ ‑ «кольцо», □ ‑ динамическая
Как и ожидалось (п. 3.1), для функции Розенброка (рисунок 2а) наибольшее среднее число побед (примерно 60%) обеспечивает топология «клика». Для функций Химмельблау и Растригина (рисунки 2б, 2в) в среднем в 90% случаев побеждает алгоритм с топологией «кольцо».
Среднее число итераций. На рисунке 3 представлена диаграмма зависимости среднего числа итераций ![]() от величины
от величины ![]()
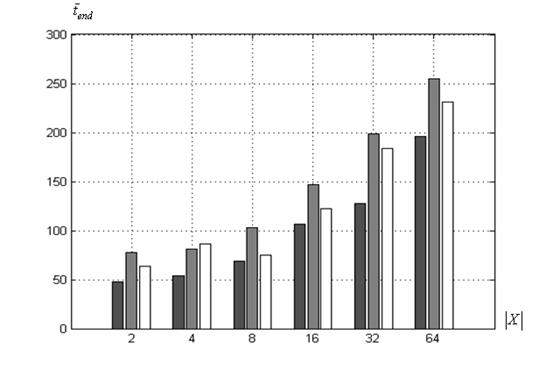
Рисунок 3 – Среднее число итераций ![]() в зависимости от величины
в зависимости от величины ![]() : ко-алгоритм
: ко-алгоритм ![]() ; ■ – функция Розенброка, ■ ‑ Химмельблау, □ ‑ Растригина
; ■ – функция Розенброка, ■ ‑ Химмельблау, □ ‑ Растригина
Рисунок 3 показывает, что для всех рассмотренных тестовых функций сходимость итерационного процесса к глобальному минимуму в худшем случае (при ![]() ) достигается в среднем за 225 итераций. Это значение почти в два раза меньше аналогичной величины для канонического алгоритма PSO(п. 3.1). Ожидаемо, при всех значениях
) достигается в среднем за 225 итераций. Это значение почти в два раза меньше аналогичной величины для канонического алгоритма PSO(п. 3.1). Ожидаемо, при всех значениях ![]() быстрее всего вычислительный процесс достигает состояния стагнации для унимодальной функции Розенброка. Неожиданным является то обстоятельство, что то же состояние для многоэкстремальной функции Растригина достигается, в среднем, при меньшем числе итераций, чем для всего лишь четырехэкстремальной функции Химмельблау. Для объяснения этого феномена необходимы дополнительные исследования.
быстрее всего вычислительный процесс достигает состояния стагнации для унимодальной функции Розенброка. Неожиданным является то обстоятельство, что то же состояние для многоэкстремальной функции Растригина достигается, в среднем, при меньшем числе итераций, чем для всего лишь четырехэкстремальной функции Химмельблау. Для объяснения этого феномена необходимы дополнительные исследования.
Среднее число испытаний. Диаграмма зависимости среднего числа испытаний ![]() от величины
от величины ![]() для суброя-победителя представлена на рисунке 4.
для суброя-победителя представлена на рисунке 4.
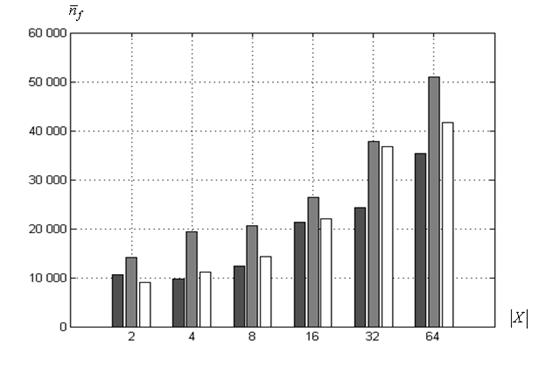
Рисунок 4 – Среднее число испытаний ![]() для суброя-победителя в зависимости от величины
для суброя-победителя в зависимости от величины ![]() : ко-алгоритм
: ко-алгоритм ![]() ; ■ – функция Розенброка, ■ ‑ Химмельблау, □ ‑ Растригина
; ■ – функция Розенброка, ■ ‑ Химмельблау, □ ‑ Растригина
Из рисунка 4 следует, что для суброя-победителя в худшем случае (при ![]() среднее число испытаний
среднее число испытаний ![]() не превышает 53 000. Эта величина почти в 1,5 раза выше аналогичного значения для канонического алгоритма PSO(таблица 2). Меньшее среднее число испытаний ко-алгоритм
не превышает 53 000. Эта величина почти в 1,5 раза выше аналогичного значения для канонического алгоритма PSO(таблица 2). Меньшее среднее число испытаний ко-алгоритм ![]() обеспечивает, как правило, для функции Розенброка, большее число – для функции Химмельблау.
обеспечивает, как правило, для функции Розенброка, большее число – для функции Химмельблау.
Размеры суброев. На рисунке 5 представлены зависимости размера суброя-победителя ![]() в момент окончания итерационного процесса от величины
в момент окончания итерационного процесса от величины ![]() , а также зависимости
, а также зависимости ![]() ,
, ![]() .
.
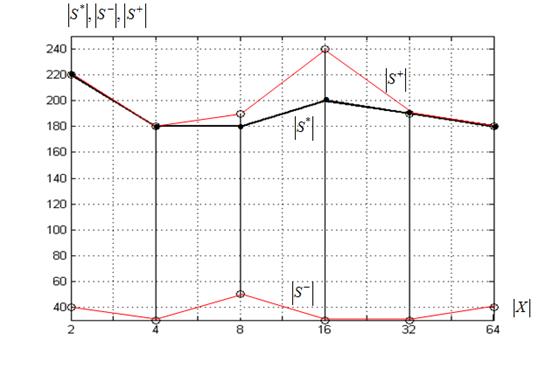
а) функция Розенброка
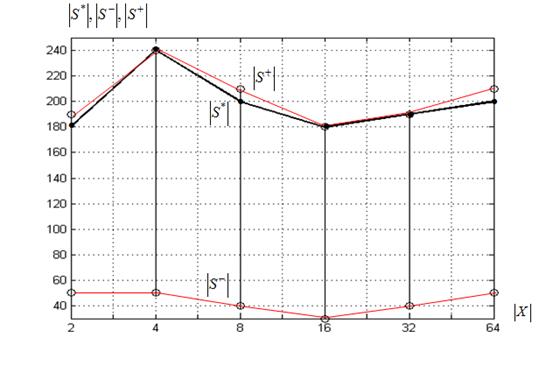
б) функция Химмельблау
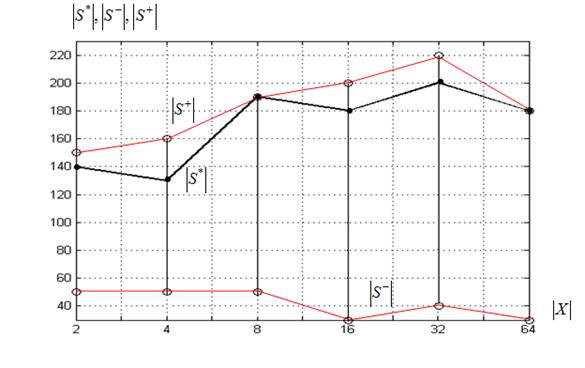
в) функция Растригина
Рисунок 5 – Размеры суброев-победителей ![]() в момент окончания итерационного процесса в функции величины
в момент окончания итерационного процесса в функции величины ![]() : алгоритм
: алгоритм ![]()
Рисунок показывает, что для всех исследуемых функций интервал изменения величины ![]() равен
равен ![]() . Для всех рассматриваемых тестовых функций и размерностей вектора
. Для всех рассматриваемых тестовых функций и размерностей вектора ![]() , суброй-победитель в своей эволюции проходит этап, когда число частиц в нем близко к минимально допустимому
, суброй-победитель в своей эволюции проходит этап, когда число частиц в нем близко к минимально допустимому ![]() . Достигнув своего максимального размера суброй-победитель, как правило, не уменьшается или уменьшается незначительно. Отметим еще то обстоятельство, что не всегда суброй-победитель в момент перехода итерационного процесса в состояние стагнации достигает своего максимального размера.
. Достигнув своего максимального размера суброй-победитель, как правило, не уменьшается или уменьшается незначительно. Отметим еще то обстоятельство, что не всегда суброй-победитель в момент перехода итерационного процесса в состояние стагнации достигает своего максимального размера.
3.3. Ко-алгоритм Co-PSO![]()
Исследование выполнено для трех вариантов ко-алгоритма ![]() :
: ![]() ,
, ![]() ,
, ![]() . Все суброи в этих вариантах используют топологии «клика», «кольцо» и динамическую топологию соответственно.
. Все суброи в этих вариантах используют топологии «клика», «кольцо» и динамическую топологию соответственно.
Оценка вероятности локализации глобального экстремума. Диаграммы зависимости оценки ![]() от величины
от величины ![]() приведены на рисунке 6.
приведены на рисунке 6.
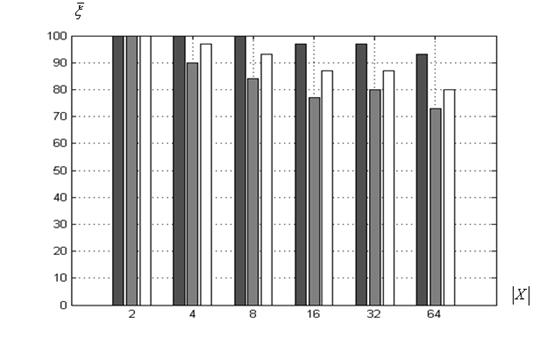
а) функция Розенброка

б) функция Химмельблау
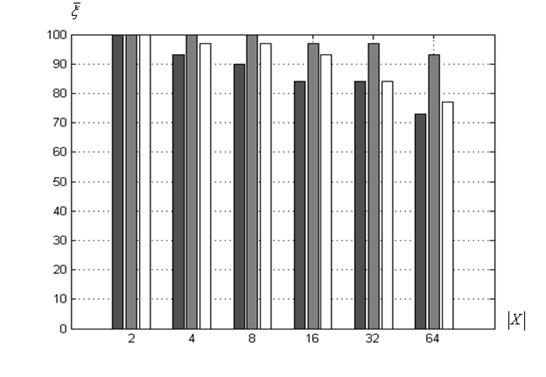
в) функция Растригина
Рисунок 6 – Оценка вероятности ![]() в функции величины
в функции величины ![]() : ■ – ко-алгоритм
: ■ – ко-алгоритм ![]() ; ■ ‑
; ■ ‑ ![]() ; □ ‑
; □ ‑ ![]()
Рисунок 6 показывает следующее. Ожидаемо (п. 3.1), для функции Розенброка (рисунок 6а) при любых значениях ![]() максимальную оценку
максимальную оценку ![]() обеспечивает ко-алгоритм
обеспечивает ко-алгоритм ![]() , а минимальную оценку – ко-алгоритм
, а минимальную оценку – ко-алгоритм ![]() . В случае функции Химмельблау (рисунок 6б) все три ко-алгоритма показывают близкие результаты. Для функции Растригина (рисунок 6в) во всех случаях лучшая оценка
. В случае функции Химмельблау (рисунок 6б) все три ко-алгоритма показывают близкие результаты. Для функции Растригина (рисунок 6в) во всех случаях лучшая оценка ![]() получается с помощью ко-алгоритма
получается с помощью ко-алгоритма ![]() , а худшая – ко-алгоритма
, а худшая – ко-алгоритма ![]() . В худшем случае (при
. В худшем случае (при ![]() ) оценка
) оценка ![]() достигает величины, равной примерно 84%.
достигает величины, равной примерно 84%.
В целом, данное исследование показывает, что ко-алгоритм ![]() обеспечивает более низкую оценку вероятности
обеспечивает более низкую оценку вероятности ![]() в сравнении с ко-алгоритмом
в сравнении с ко-алгоритмом ![]() , но более высокую оценку, чем канонический алгоритм PSO (п. 3.1).
, но более высокую оценку, чем канонический алгоритм PSO (п. 3.1).
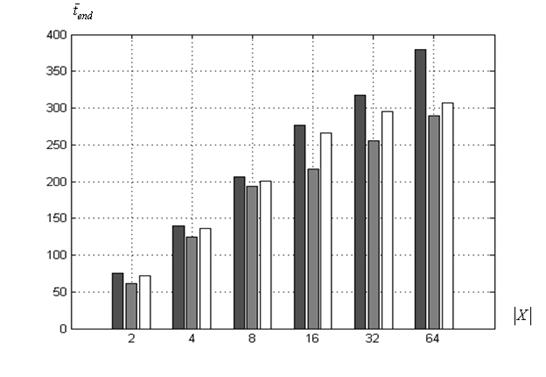
Среднее число итераций. На рисунке 7 представлены диаграммы зависимости среднего числа итераций ![]() от величины
от величины ![]() .
.

а) функция Розенброка
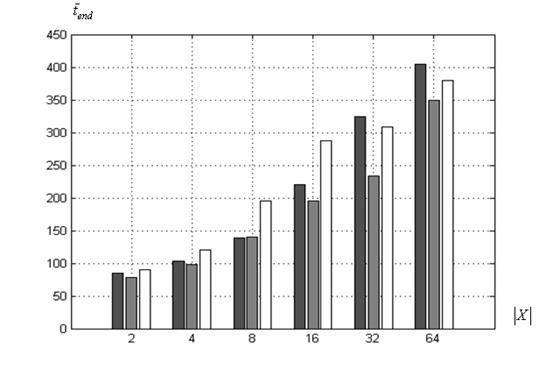
б) функция Химмельблау
в) функция Растригина
Рисунок 7 – Среднее число итераций ![]() в функции величины
в функции величины ![]() : ■ – ко-алгоритм
: ■ – ко-алгоритм![]() , ■ ‑
, ■ ‑ ![]() , □ ‑
, □ ‑ ![]()
Рисунок 7 иллюстрирует следующие факты. Для функции Розенброка (рисунок 7а) наименьшее значение величины ![]() зафиксировано у ко-алгоритма
зафиксировано у ко-алгоритма ![]() , а наибольшее – у алгоритма
, а наибольшее – у алгоритма ![]() . В случае функции Химмельблау (рисунок 7б) минимальное значение величины
. В случае функции Химмельблау (рисунок 7б) минимальное значение величины ![]() , преимущественно, показывает ко-алгоритм
, преимущественно, показывает ко-алгоритм ![]() . Для функции Растригина (рисунок 7в) лучшие результаты с точки зрения величины
. Для функции Растригина (рисунок 7в) лучшие результаты с точки зрения величины ![]() также обеспечивает ко-алгоритм
также обеспечивает ко-алгоритм ![]() . Рисунок 7 показывает, кроме того, что, в худшем случае (при
. Рисунок 7 показывает, кроме того, что, в худшем случае (при ![]() ), для всех трех рассматриваемых тестовых функций величина
), для всех трех рассматриваемых тестовых функций величина ![]() составляет примерно 324 итерации. Этот результат хуже, чем зафиксированный для алгоритма
составляет примерно 324 итерации. Этот результат хуже, чем зафиксированный для алгоритма ![]() , но лучше результата, который показал канонический алгоритм PSO(п. 3.1).
, но лучше результата, который показал канонический алгоритм PSO(п. 3.1).
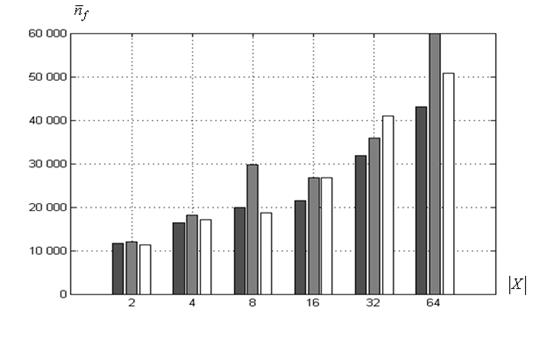
Среднее число испытаний. Зависимость среднего числа испытаний ![]() от величины
от величины ![]() иллюстрирует рисунок 8.
иллюстрирует рисунок 8.
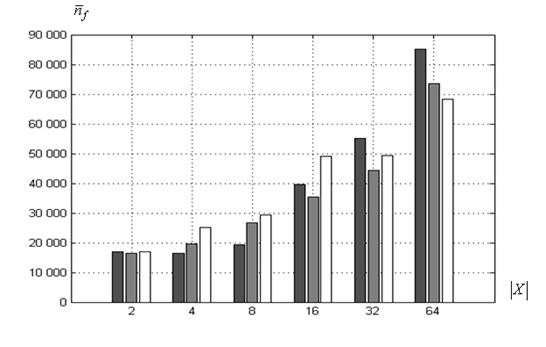
а) функция Розенброка
б) функция Химмельблау
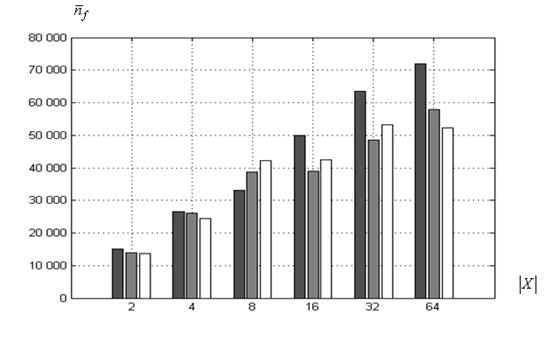
в) функция Растригина
Рисунок 8 – Среднее число испытаний ![]() в функции величины
в функции величины ![]() : ■ – ко-алгоритм
: ■ – ко-алгоритм![]() , ■ ‑
, ■ ‑ ![]() , □ ‑
, □ ‑ ![]()
Из рисунка 8а следует, что для функции Розенброка минимальное значение величины ![]() в большинстве случаев соответствует ко-алгоритму
в большинстве случаев соответствует ко-алгоритму ![]() , а максимальное значение ‑ ко-алгоритму
, а максимальное значение ‑ ко-алгоритму ![]() . Для функции Химмельблау явного лидера по среднему числу испытаний
. Для функции Химмельблау явного лидера по среднему числу испытаний ![]() рисунок 8б не выявляет. В случае функции Растригина (рисунок 8в) минимальная величина
рисунок 8б не выявляет. В случае функции Растригина (рисунок 8в) минимальная величина ![]() соответствует ко-алгоритмам
соответствует ко-алгоритмам ![]() ,
, ![]() . При
. При ![]() (худший случай) величина
(худший случай) величина ![]() для суброя-победителя для всех рассматриваемых тестовых функциях примерно равна 64 000. Эта величина почти в два раза выше аналогичного значения для канонического алгоритма PSO(п. 3.1) и примерно на 30% выше того же значения для алгоритма
для суброя-победителя для всех рассматриваемых тестовых функциях примерно равна 64 000. Эта величина почти в два раза выше аналогичного значения для канонического алгоритма PSO(п. 3.1) и примерно на 30% выше того же значения для алгоритма ![]()
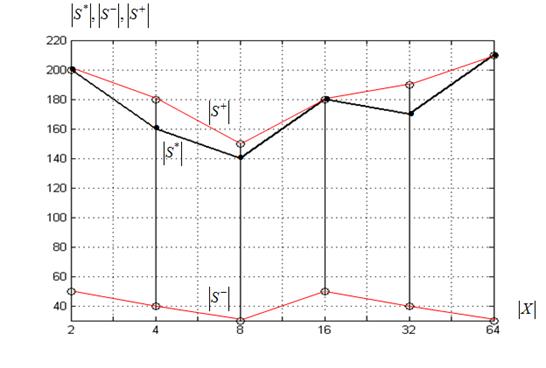
Размеры суброев. На рисунке 9 представлены графики зависимости конечных размеров суброев-победителей ![]() от величины
от величины ![]() , а также аналогичные графики зависимостей
, а также аналогичные графики зависимостей ![]() ,
, ![]() . Из всех результатов исследования представляем четыре: ко-алгоритм
. Из всех результатов исследования представляем четыре: ко-алгоритм ![]() и функция Розенброка; ко-алгоритмы
и функция Розенброка; ко-алгоритмы ![]() ,
, ![]() и функция Химмельблау; ко-алгоритм
и функция Химмельблау; ко-алгоритм ![]() и функция Растригина.
и функция Растригина.

а) ко-алгоритм ![]() , функция Розенброка
, функция Розенброка
б) ко-алгоритм ![]() , функция Химмельблау
, функция Химмельблау
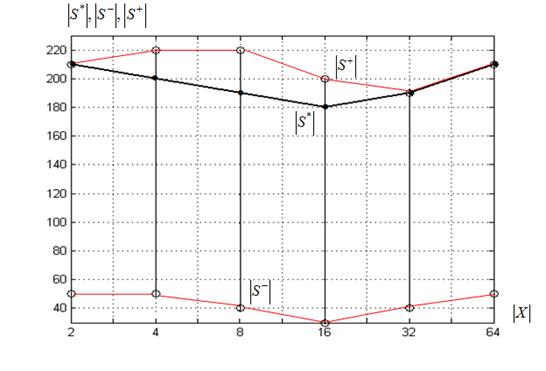
в) ко-алгоритм ![]() , функция Химмельблау
, функция Химмельблау
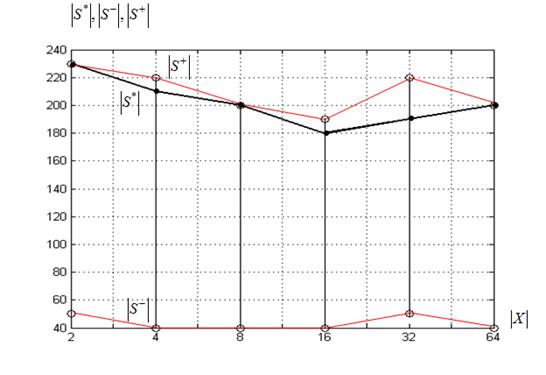
г) ко-алгоритм ![]() , функция Растригина
, функция Растригина
Рисунок 9 – Предельные размеры суброев ![]() в функции величины
в функции величины ![]()
Из рисунка 9 следует, что для суброя-победителя минимальная величина ![]() равна 20, а максимальная ‑ 240. Характер поведения предельных размеров суброев-победителей близок к аналогичным результатам, полученным для алгоритма
равна 20, а максимальная ‑ 240. Характер поведения предельных размеров суброев-победителей близок к аналогичным результатам, полученным для алгоритма ![]() (см. выше).
(см. выше).
Величины свободных параметров ![]() суброев-победителей. На рисунке 10 представлены диаграммы значений свободных параметров
суброев-победителей. На рисунке 10 представлены диаграммы значений свободных параметров ![]() суброев-победителей в функции величины
суброев-победителей в функции величины ![]() .
.
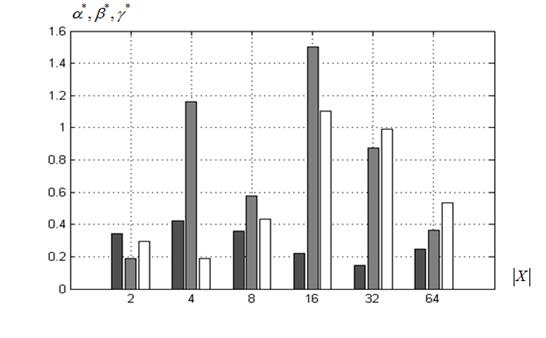
а) ко-алгоритм ![]() , функция Розенброка
, функция Розенброка
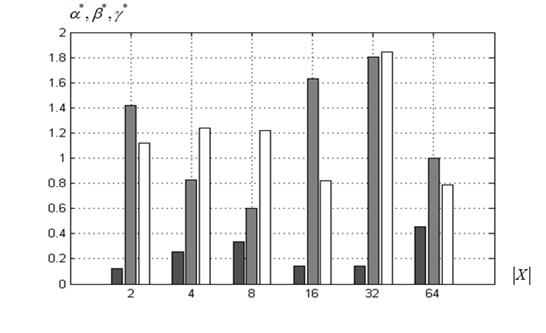
б) ко-алгоритм ![]() , функция Химмельблау
, функция Химмельблау
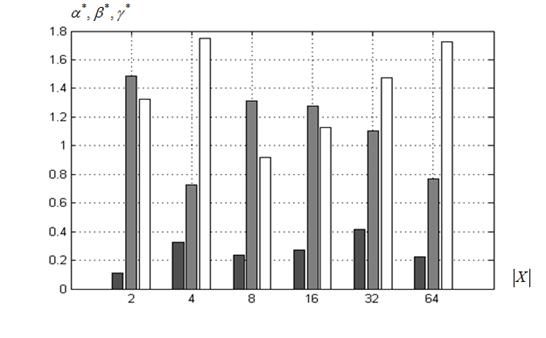
в) ко-алгоритм ![]() , функция Химмельблау
, функция Химмельблау
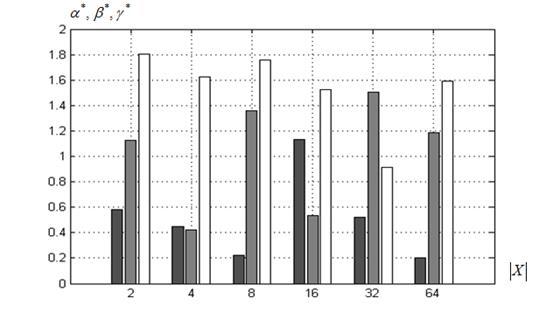
г) ко-алгоритм ![]() , функция Растригина
, функция Растригина
Рисунок 10 – Значения свободных параметров ![]() суброев-победителей в функции величины
суброев-победителей в функции величины ![]() : ■ – параметр
: ■ – параметр![]() , ■ ‑
, ■ ‑ ![]() , □ ‑
, □ ‑ ![]()
Рисунок 10 показывает, что во всех экспериментах полученные значения свободных параметров значительно отличаются от рекомендованных (п. 3.1). Так, оказалось, что значение инерционного параметра ![]() во всех случаях не превышает значения 0,6, в то время как рекомендованное значение равно 0,7298. Значения социальной и когнитивной компонент изменяются в широком диапазоне [0,2; 1,8].
во всех случаях не превышает значения 0,6, в то время как рекомендованное значение равно 0,7298. Значения социальной и когнитивной компонент изменяются в широком диапазоне [0,2; 1,8].
Таким образом, вычислительный эксперимент показал, что по всем рассмотренным индикаторам эффективности ко-алгоритмы ![]() и
и ![]() превосходят канонический алгоритм PSO. Эффективность ко-алгоритма
превосходят канонический алгоритм PSO. Эффективность ко-алгоритма ![]() в большинстве случаев оказалась выше эффективности ко-алгоритма
в большинстве случаев оказалась выше эффективности ко-алгоритма ![]() .
.
4. Задача об управляемом спуске космического аппарата
Рассматриваем задачу оптимального управления спуском космического аппарата в атмосфере Земли [9]. Используем уточненную постановку задачи из работы [3].
Начало системы координат ![]() , в которой рассматриваем движение аппарата, находится в центре Земли. Ось
, в которой рассматриваем движение аппарата, находится в центре Земли. Ось ![]() направлена на исходное положение аппарата, ось
направлена на исходное положение аппарата, ось ![]() - в сторону его движения и перпендикулярна оси
- в сторону его движения и перпендикулярна оси ![]() , ось
, ось ![]() образует с указанными осями правую тройку.
образует с указанными осями правую тройку.
Математическую модель объекта управления представляет система обыкновенных дифференциальных уравнений (ОДУ)
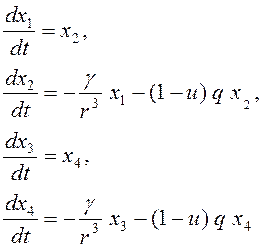 (11)
(11)
при заданных начальных условиях ![]() ,
, ![]() . Приняты следующие обозначения:
. Приняты следующие обозначения: ![]() - координаты центра масс космического аппарата;
- координаты центра масс космического аппарата; ![]() - компоненты его скорости;
- компоненты его скорости; ![]() - управление;
- управление; ![]() - величина радиус-вектора аппарата;
- величина радиус-вектора аппарата; ![]() – гравитационная постоянная Земли;
– гравитационная постоянная Земли; 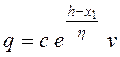 - составляющая аэродинамической силы;
- составляющая аэродинамической силы; ![]() - величина скорости аппарата; c – его аэродинамическая характеристика; h – высота атмосферы;
- величина скорости аппарата; c – его аэродинамическая характеристика; h – высота атмосферы; ![]() – согласующий коэффициент модели атмосферы [3].
– согласующий коэффициент модели атмосферы [3].
Определены функционалы качества управления
 , (12)
, (12)
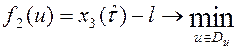 , (13)
, (13)
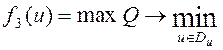 , (14)
, (14)
имеющие смысл максимальной перегрузки, отклонения от заданной точки на поверхности Земли и максимальной амплитуды перегрузки соответственно. Здесь ![]() км – радиус Земли,
км – радиус Земли, ![]() м/c2 – ускорение свободного падения,
м/c2 – ускорение свободного падения, ![]() – длительность полета, l– координата по оси
– длительность полета, l– координата по оси ![]() заданной точки на поверхности Земли,
заданной точки на поверхности Земли, ![]() - множество допустимых управлений,
- множество допустимых управлений, ![]() - заданные константы.
- заданные константы.
Задача представляет собой трехкритериальную задачу оптимального управления динамической системой и состоит в определении допустимого управления ![]() , доставляющего минимум критериям оптимальности (12) – (14).
, доставляющего минимум критериям оптимальности (12) – (14).
Не смотря на известный недостаток решения задач многокритериальной оптимизации с помощью скалярной свертки их частных критериев оптимальности [10], применяем именно этот метод. Используем аддитивную скалярную свертку
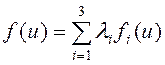 , (15)
, (15)
где ![]() – весовой коэффициент, учитывающий относительную важность функционала
– весовой коэффициент, учитывающий относительную важность функционала ![]() . В результате получаем однокритериальную задачу оптимального управления динамической системой (11) с критерием оптимальности (15).
. В результате получаем однокритериальную задачу оптимального управления динамической системой (11) с критерием оптимальности (15).
Аналогично тому, как это сделано в работе [3], сводим полученную задачу оптимального управления к задаче нелинейного программирования.
Покрываем интервал ![]() равномерной сеткой с узлами
равномерной сеткой с узлами ![]()
![]() и отыскиваем оптимальное управление
и отыскиваем оптимальное управление ![]() в классе кусочно-линейных функций (рисунок 11).
в классе кусочно-линейных функций (рисунок 11).
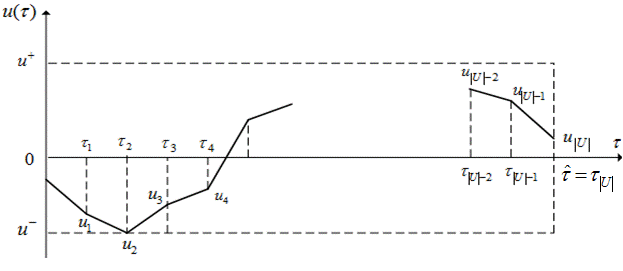
Рисунок 11 – Кусочно-линейная аппроксимация управления ![]()
Обозначаем ![]() , где
, где ![]() . Тогда указанная выше однокритериальная задача оптимального управления принимает вид
. Тогда указанная выше однокритериальная задача оптимального управления принимает вид
 , (16)
, (16)
где ![]() . Таким образом, имеем задачу глобальной условной оптимизации (16) с целевой функцией (15), вектором варьируемых параметров U и множеством его допустимых значений
. Таким образом, имеем задачу глобальной условной оптимизации (16) с целевой функцией (15), вектором варьируемых параметров U и множеством его допустимых значений ![]() .
.
4.2. Вычислительный эксперимент
Эксперимент выполнен при следующих начальных условиях космического аппарата: ![]() км,
км, ![]() ,
, ![]() км/c,
км/c, ![]() км/с. Поскольку снижение значения максимальной перегрузки является приоритетным, задаем следующие значения весовых коэффициентов
км/с. Поскольку снижение значения максимальной перегрузки является приоритетным, задаем следующие значения весовых коэффициентов ![]() :
:
![]() .
.
Размерность вектора ![]() принимаем равной 50.
принимаем равной 50.
Специальное исследование показало, что система ОДУ (11) является нежесткой. Поэтому для интегрирования этой системы используем метод Рунге-Кутты 4-го порядка.
Задачу решаем с использованием ко-алгоритма ![]() с пятью ко-эволюционирующими суброями, каждый из которых имеют топологию соседства частиц типа «клика» и отличается от других суброев значениями своих параметров
с пятью ко-эволюционирующими суброями, каждый из которых имеют топологию соседства частиц типа «клика» и отличается от других суброев значениями своих параметров ![]() . Приняты следующие значения свободных параметров ко-алгоритма: интервал адаптации
. Приняты следующие значения свободных параметров ко-алгоритма: интервал адаптации ![]() , величина штрафа
, величина штрафа ![]() , минимально допустимый размер суброя
, минимально допустимый размер суброя ![]() . Размер роя равен
. Размер роя равен ![]() . В процессе инициализации роя все субпопуляции получают число частиц, равное 20. Поскольку размерность вектора варьируемых параметров велика (равна 51), а априорная информация о ландшафте целевой функции
. В процессе инициализации роя все субпопуляции получают число частиц, равное 20. Поскольку размерность вектора варьируемых параметров велика (равна 51), а априорная информация о ландшафте целевой функции ![]() отсутствует, для повышения вероятности локализации глобального экстремума используем мультистарт с числом запусков алгоритма
отсутствует, для повышения вероятности локализации глобального экстремума используем мультистарт с числом запусков алгоритма ![]() . Число итераций ко-алгоритма ограничиваем величиной
. Число итераций ко-алгоритма ограничиваем величиной ![]() .
.
Рисунок 12 иллюстрирует сходимость вычислительного процесса при решении задачи с помощью ко-алгоритма ![]() и канонического алгоритма PSO соответственно. Заметим, что не учитывает максимальную амплитуду перегрузки
и канонического алгоритма PSO соответственно. Заметим, что не учитывает максимальную амплитуду перегрузки ![]() [3].
[3].

а) ко-алгоритм ![]() : суброй-победитель
: суброй-победитель
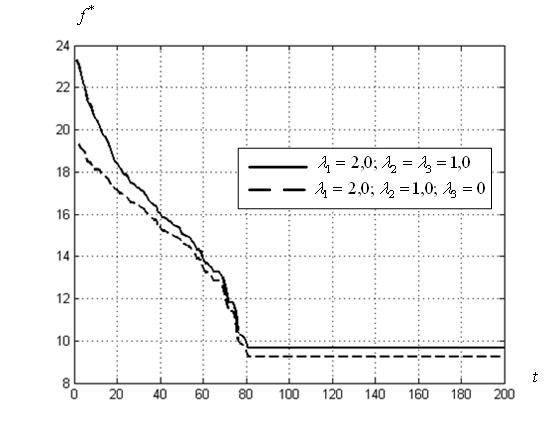
б) канонический алгоритм PSO
Рисунок 12 – Сходимость вычислительного процесса для лучшего по мультистарту запуска алгоритма и суброя-победителя
Рисунок показывает значительное превосходство в скорости сходимости ко-алгоритма ![]() над каноническим алгоритмом PSO. Лучшее, достигнутое ко-алгоритмом
над каноническим алгоритмом PSO. Лучшее, достигнутое ко-алгоритмом ![]() значение целевой функцией, равно
значение целевой функцией, равно ![]() , а аналогичное значение для канонического алгоритма PSO‑
, а аналогичное значение для канонического алгоритма PSO‑ ![]() . Таким образом, из рисунка следует, что ко-алгоритм
. Таким образом, из рисунка следует, что ко-алгоритм ![]() по сравнению с каноническим алгоритмом PSOобеспечивает не только более высокую скорость сходимости, но и более высокую точность локализации глобального экстремума целевой функции.
по сравнению с каноническим алгоритмом PSOобеспечивает не только более высокую скорость сходимости, но и более высокую точность локализации глобального экстремума целевой функции.
Представляет интерес рисунок 13, иллюстрирующий характер сходимости итерационного процесса для каждого из суброев ко-алгоритма ![]() (вариант
(вариант ![]() ). Победителем в данном эксперименте стал суброй
). Победителем в данном эксперименте стал суброй ![]() , который обеспечил значения критериев оптимальности, равные
, который обеспечил значения критериев оптимальности, равные ![]() .
.
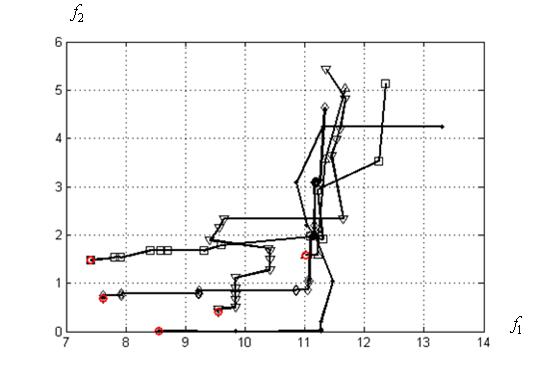
Рисунок 13 – Сходимость лучшего по мультистарту запуска алгоритма: вариант ![]() ; ко-алгоритм
; ко-алгоритм ![]() ;
;
‑, ∆, □, ◊, ![]() ‑ суброи
‑ суброи ![]() –
– ![]() соответственно; красные маркеры соответствуют концу итерационного процесса
соответственно; красные маркеры соответствуют концу итерационного процесса
На рисунке 14 представлены зависимости численности ![]() суброев ко-алгоритма в функции номера итерации t;
суброев ко-алгоритма в функции номера итерации t; ![]() . Зависимость победившего суброя (имеющего номер 4) выделена красным цветом.
. Зависимость победившего суброя (имеющего номер 4) выделена красным цветом.
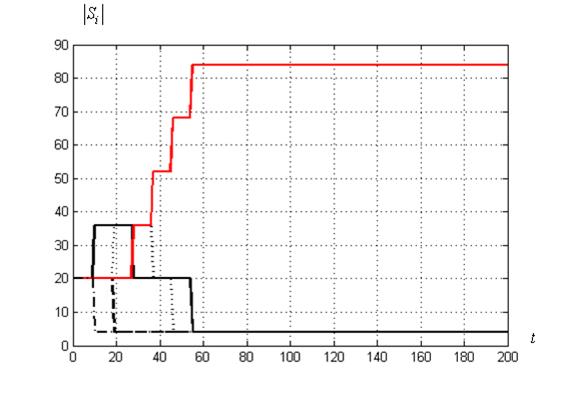
Рисунок 14 – Численности ![]() суброев в функции номера итерации для лучшего по мультистарту запуска алгоритма: ко-алгоритм
суброев в функции номера итерации для лучшего по мультистарту запуска алгоритма: ко-алгоритм ![]() ;
; ![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ‑ суброи
‑ суброи ![]() –
– ![]() соответственно
соответственно
Рисунок 14 показывает, что после первого интервала адаптации лидером становится суброй ![]() . Суброй-победитель
. Суброй-победитель ![]() начинает лидировать после третьего интервала адаптации и сохраняет свое лидерство до завершения итерационного процесса, когда число частиц в нем становится равным 84.
начинает лидировать после третьего интервала адаптации и сохраняет свое лидерство до завершения итерационного процесса, когда число частиц в нем становится равным 84.
Диаграмма значений свободных параметров ![]() суброев
суброев ![]() приведена на рисунке 15. Примечательно, что значения этих параметров суброя-победителя наиболее близки к их рекомендованным значениям (п. 1) и составляют 0,9846, 1,13299, 1,6412 соответственно.
приведена на рисунке 15. Примечательно, что значения этих параметров суброя-победителя наиболее близки к их рекомендованным значениям (п. 1) и составляют 0,9846, 1,13299, 1,6412 соответственно.
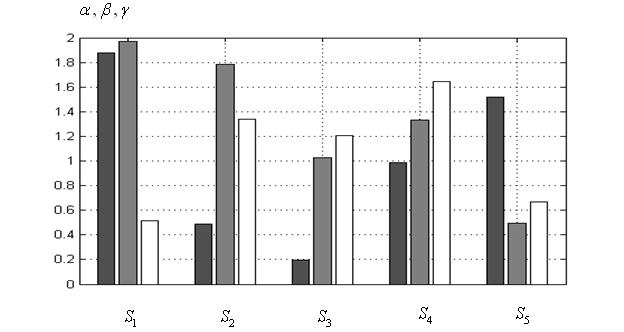
Рисунок 15 – Значения свободных параметров суброев ко-алгоритма ![]() для лучшего по мультистарту запуска: ■ – параметр
для лучшего по мультистарту запуска: ■ – параметр ![]() , ■ ‑
, ■ ‑ ![]() , □ ‑
, □ ‑ ![]()
Полученная в вычислительном эксперименте траектория спуска космического аппарата представлена на рисунке 16. Минимальное отклонение от заданного места посадки, достигнутое алгоритмом ![]() , составляет 0,68 км, а каноническим алгоритмом PSO – 0,92 км.
, составляет 0,68 км, а каноническим алгоритмом PSO – 0,92 км.
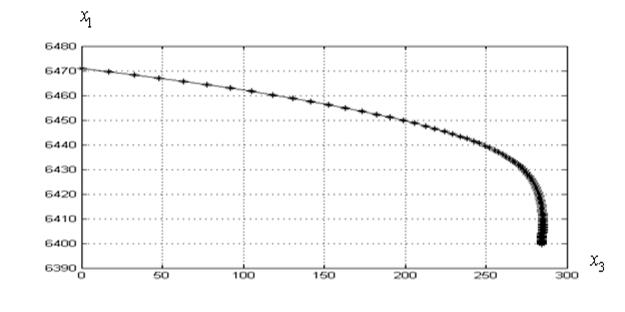
Рисунок 16 – Траектория спуска космического аппарата для лучшего по мультистарту запуска алгоритма; ко-алгоритм ![]()
Показательным является рисунок 17, на котором приведены максимальные перегрузки ![]() в функции времени спуска
в функции времени спуска ![]() космического аппарата, полученные с помощью ко-алгоритма
космического аппарата, полученные с помощью ко-алгоритма ![]() и канонического алгоритма PSO. Пунктирные линии на графиках соответствуют начальному приближению управления
и канонического алгоритма PSO. Пунктирные линии на графиках соответствуют начальному приближению управления ![]() , сплошные линии – найденному оптимальному управлению
, сплошные линии – найденному оптимальному управлению ![]() (в момент
(в момент ![]() окончания итерационного процесса). Перегрузка обусловлена действием аэродинамической силы, пропорциональной квадрату скорости космического аппарата. После 250-ой секунды спуска эта скорость становится относительно малой и колебания перегрузки несущественны. Поэтому графики ограничены этим временем.
окончания итерационного процесса). Перегрузка обусловлена действием аэродинамической силы, пропорциональной квадрату скорости космического аппарата. После 250-ой секунды спуска эта скорость становится относительно малой и колебания перегрузки несущественны. Поэтому графики ограничены этим временем.
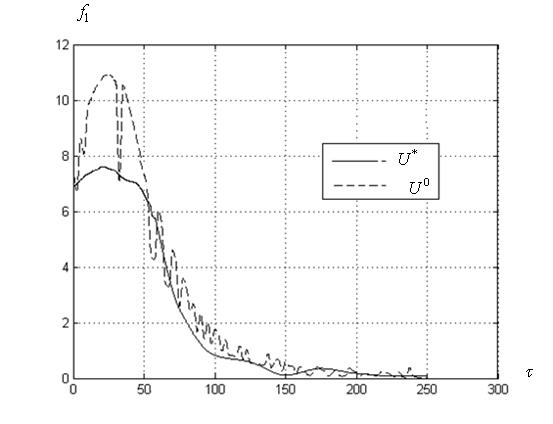
а) ко-алгоритм ![]()
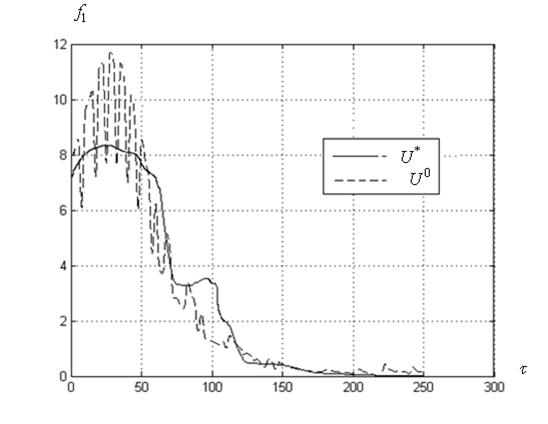
б) канонический алгоритм PSO
Рисунок 17 – Зависимость перегрузки ![]() от времени спуска космического аппарата для лучшего по мультистарту запуска алгоритма
от времени спуска космического аппарата для лучшего по мультистарту запуска алгоритма
Рисунок 18, показывает, что ко-алгоритм ![]() обеспечивает по сравнению с каноническим алгоритмом PSOзначительно более гладкую зависимость перегрузки от времени снижения космического аппарата (что подтверждают соответствующие значения критерия оптимальности
обеспечивает по сравнению с каноническим алгоритмом PSOзначительно более гладкую зависимость перегрузки от времени снижения космического аппарата (что подтверждают соответствующие значения критерия оптимальности ![]() ).
).
Приведем, наконец, оптимальные управления, найденные ко-алгоритмом ![]() и каноническим алгоритмом PSO, которым соответствуют представленные выше результаты (рисунок 18).
и каноническим алгоритмом PSO, которым соответствуют представленные выше результаты (рисунок 18).
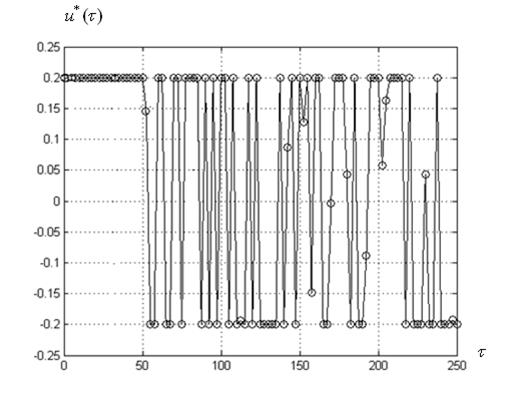
а) ко-алгоритм ![]()
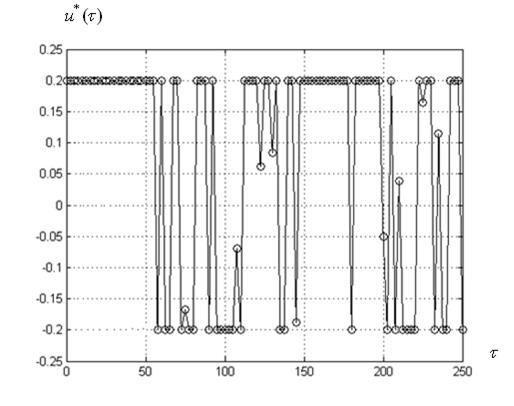
б) канонический алгоритм PSO
Рисунок 18 – Варианты оптимального управления ![]() для лучшего по мультистарту запуска алгоритма
для лучшего по мультистарту запуска алгоритма
Известно, что характерной особенностью рассматриваемой динамической системы является оптимальность в ней, так называемых, скользящих режимов, когда, в пределе, управление переключается между своими минимально и максимально допустимыми значениями с бесконечной частотой. Заметим, что именно это обстоятельство делает рассматриваемую задачу сложной с вычислительной точки зрения. Рисунок 20 показывает, что ко-алгоритм ![]() обеспечивает гораздо более хорошее приближение к указанному режиму, чем канонический алгоритм PSO.
обеспечивает гораздо более хорошее приближение к указанному режиму, чем канонический алгоритм PSO.
В работе предложен ко-эволюционный алгоритм глобальной оптимизации Co-PSO, основанный на алгоритме роя частиц. Ко-алгоритм предполагает параллельное (по крайней мере, на логическом уровне) функционирование заданного числа субалгоритмов PSO, которые используют различные топологии соседства частиц и/или различные значения своих свободных параметров.
Представлен MatLab-комплекс программ, реализующих алгоритм Co-PSO и канонический алгоритм роя частиц PSO.
Выполнен широкий вычислительный эксперимент по исследованию эффективности алгоритма Co-PSO и реализующего его программного обеспечения. В эксперименте использованы тестовые функции Розенброка, Химмельблау и Растригина. Результаты исследования показывают превосходство алгоритма Co-PSO над каноническим алгоритмом PSO по ряду критериев эффективности.
С помощью разработанного алгоритмического и программного обеспечения решена трехкритериальная задача оптимального управления космическим аппаратом на этапе его спуска в атмосфере Земли. Результаты решения показали высокую эффективность предложенных алгоритмических и программных решений.
В развитие работы авторы планируют параллельную реализацию и исследование параллельной версии ко-алгоритма Co-PSO.
Список литературы
1. Воробьева Е.Ю., Карпенко А.П., Селиверстов Е.Ю. Ко-гибридизация алгоритмов роя частиц // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журнал. 2012. № 4. Режим доступа: http://www.technomag.edu.ru/doc/355729.html (дата обращения 27.08.2013).
2. Karpenko A.P., Svianadze Z.O. Meta-optimization based on self-organizing map and genetic algorithm // Optical Memory and Neural Networks (Information Optics). 2011. Vol. 20, no. 4. P. 279-283. http://dx.doi.org/10.3103/S1060992X11040059
3. Карпенко А.П., Митина Е.В., Семенихин А.С. Когенетический алгоритм Парето-аппроксимации в задаче многокритериальной оптимизации // Информационные технологии. 2013. № 1. С. 22-32.
4. Карпенко А.П., Селиверстов Е.Ю. Глобальная оптимизация методом роя частиц. Обзор // Информационныетехнологии. 2010. № 2. С. 25-34.
5. Yongquan Zhou, Shengyu Pei. A hybrid co-evolutionary particle swarm optimization algorithm for solving constrained engineering design problems // China: Journal of computers. 2010. Vol. 5, no. 6. P. 965-972.
6. Yuhui Shi, Renato A. Krohling. Co-evolutionary particle swarm optimization to solve min-max problems // USA: Proceedings of the Evolutionary Computation. 2002. Vol. 2. P. 1682-1687.
7. Yang Sun, Lingbo Zhang, Xingsheng Gu. Co-evolutionary cultural based particle swarm optimization algorithm // China: Life system modeling and intelligent. Communications in computer and information science. 2010. Vol. 98, no. 1. P. 1-7.
8. Jie J., Han Ch., Zeng J. An Extended Mind Evolutionary Computation Model for Optimizations // Applied Mathematics and Computation. 2007. Vol. 185, no. 2. P. 1038-1049.
9. Федоренко Р.П. Приближенное решение задач оптимального управления. М.: Наука, 1978. 488 с.
10. Карпенко А.П., Федорук В.Г. Один класс прямых адаптивных методов многокритериальной оптимизации // Информационные технологии. 2009. № 5. C. 24-30.
Публикации с ключевыми словами: алгоритм роя частиц, гибридизация, ко-эволюция
Публикации со словами: алгоритм роя частиц, гибридизация, ко-эволюция
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



