научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2013
DOI: 10.7463/1013.0615247
УДК 621.378:551.508
Россия, МГТУ им. Н.Э. Баумана
Введение
Для эффективного мониторинга атмосферы и оперативного контроля многокомпонентных газовых смесей требуется создание высокочувствительных быстродействующих газоанализаторов, способных дистанционно или локально контролировать содержание в атмосферном воздухе загрязняющих газовых компонент. Лазерные методы являются наиболее перспективными для оперативного газоанализа многокомпонентных смесей [1-6].
Если качественный состав газовой смеси известен, то измерение концентраций компонент смеси (количественный анализ смеси) может быть проведено путем проведения многоспектральных измерений (например, с помощью абсорбционного или оптико-акустического методов), используя набор лазерных излучателей или перестраиваемый по длине волны источник лазерного излучения [1-6].
Одной из проблем, возникающих в лазерном анализе при измерении количественного состава многокомпонентных газовых смесей, является необходимость применения (при определении концентраций газов смеси из многоспектральных лазерных измерений) специальных алгоритмов обработки[1-3, 7-9]. При этом трудность задачи измерения количественного состава газов существенно возрастает для сложных смесей газов, в которых концентрации компонент газовой смеси отличаются на несколько порядков или присутствуют газовые компоненты без ярко выраженных максимумов в спектрах поглощения [10, 11].
Данная статья посвящена сравнительному анализу алгоритмов восстановления концентраций газов в сложных многокомпонентных смесях из многоспектральных лазерных измерений.
1. Постановка задачи
Будем считать, что анализируемая газовая смесь содержит K газовых компонент и измерения проводятся на М длинах волн, а ширина линий генерации лазера много меньше ширины линий поглощения анализируемых газов. Тогда задача нахождения концентраций газов из результатов многоспектральных лазерных измерений сводится к решению системы линейных алгебраических уравнений лазерного газоанализа [1-3]. В матричной форме система уравнений лазерного газоанализа имеет вид
![]() , (1)
, (1)
где
![]() - матрица системы (1) размерностью
- матрица системы (1) размерностью ![]() ;
;
![]() - M-мерный искомый вектор (K компонент этого вектора соответствуют концентрациям газов);
- M-мерный искомый вектор (K компонент этого вектора соответствуют концентрациям газов);
![]() - M-мерный вектор коэффициентов неселективного ослабления;
- M-мерный вектор коэффициентов неселективного ослабления;
K - матрица коэффициентов поглощения компонент газовой смеси размерностью ![]() ;
;
![]() - K-мерный вектор концентраций газов;
- K-мерный вектор концентраций газов;
![]() - M-мерный вектор приведенных измеряемых сигналов (показателей поглощения исследуемой смеси).
- M-мерный вектор приведенных измеряемых сигналов (показателей поглощения исследуемой смеси).
Неизвестными в (1) являются компоненты вектора ![]() (парциальные концентрации газовых компонент) и компоненты вектора
(парциальные концентрации газовых компонент) и компоненты вектора ![]() (коэффициенты неселективного ослабления).
(коэффициенты неселективного ослабления).
Коэффициенты неселективного ослабления слабо зависят от длины волны.Поэтому для устранения их влияния для определения концентрации одного газа обычно измерения выполняются на паре лазерных длин волн: ![]() - длине волны, на которой поглощение исследуемым газом максимально,
- длине волны, на которой поглощение исследуемым газом максимально, ![]() - длине волны, на которой поглощение исследуемым газом практически отсутствует. Вычитая уравнения для каждой пары длин волн
- длине волны, на которой поглощение исследуемым газом практически отсутствует. Вычитая уравнения для каждой пары длин волн![]() и
и ![]() друг из друга, приходим к следующему матричному уравнению [1-3]
друг из друга, приходим к следующему матричному уравнению [1-3]
![]() , (2)
, (2)
где
![]() - М/2-мерный вектор разностей сигналов
- М/2-мерный вектор разностей сигналов ![]() ;
;
![]() - матрица размерностью
- матрица размерностью ![]() с разностями коэффициентов поглощения
с разностями коэффициентов поглощения ![]() .
.
В идеальных условиях в случае отсутствия шума измерения точные значения концентраций компонент газовой смеси (или газовых загрязнителей атмосферного воздуха) можно найти непосредственно из решения уравнений лазерного газоанализа (1), (2), используя обратную матрицу (конечно, если детерминант матрицы не равен нулю). Однако, при регистрации результатов реальных измерений правая часть уравнений (1), (2) всегда известна со случайной ошибкой, обусловленной погрешностями измерения, шумами аппаратуры и т.п.
Таким образом, в (2) вместо ![]() имеем
имеем
![]() ,
,
где
![]() - М –мерный вектор шума (погрешностей измерения
- М –мерный вектор шума (погрешностей измерения ![]() ).
).
В этих условиях попытки непосредственно обратить уравнения (1), (2) приводят к тому, что найденный обратный оператор может не обладать свойством устойчивости, т.е. малые вариации данных измерений могут приводить к большим вариациям искомых величин. Такая ситуация характерна для многокомпонентных смесей (с числом компонент обычно более пяти, шести). Выход из этой трудности заключается в использовании (при определении концентраций газовых компонент по данным многоспектрального измерений) алгоритмов обработки, основанных на методах решения некорректных математических задач [12, 13].
В настоящее время для определения концентраций газов в многокомпонентных смесях по данным многоспектрального измерений эффективно используются метод поиска квазирешений или метод регуляризации Тихонова с применением различных способов (как детерминистических, так и статистических) выбора параметра регуляризации [1-3, 14-17].
Однако, для сложных газовых смесей, в которых концентрации компонент газовой смеси отличаются на несколько порядков или присутствуют компоненты без ярко выраженных максимумов в спектрах поглощения, эти методы дают большие (многие десятки и сотни процентов) погрешности (т.е. концентрации газовых компонент практически не восстанавливаются).
Единственными на сегодняшний день методами, которые используются для определения количественного состава сложных многокомпонентных смесей из многоспектральных измерений, являются метод, основанный на построении байесовской оценки решения [10], и проекционный метод [11].
В принципе, для решения этой задачи, видимо, могла бы быть создана и модификация метода поиска квазирешений. Однако, метод поиска квазирешений требует большого объема вычислений, даже при таком эффективном алгоритме подбора решений как генетический алгоритм [2].
Ниже методом математического моделирования проводится сравнительный анализ метода, основанного на построении байесовской оценки решения, и проекционного метода для задачи восстановления из многоспектральных измерений концентраций газов в сложных многокомпонентных смесях, в которых концентрации компонент газовой смеси отличаются на несколько порядков или присутствуют компоненты без ярко выраженных максимумов в спектрах поглощения.
2. Метод, основанный на построении байесовской оценки решения
Построение байесовской оценки искомого вектора ![]() для уравнения лазерного газоанализа (1) многокомпонентной газовой смеси проводится при следующих предположениях:
для уравнения лазерного газоанализа (1) многокомпонентной газовой смеси проводится при следующих предположениях:
1). Вектор шума измерения ![]() подчиняется нормальному распределению, некоррелирован с измеряемым сигналом и имеет нулевое среднее значение и корреляционную матрицу
подчиняется нормальному распределению, некоррелирован с измеряемым сигналом и имеет нулевое среднее значение и корреляционную матрицу ![]() .
.
2). Априорное распределение искомого вектора ![]() также является нормальным с некоторым средним значением
также является нормальным с некоторым средним значением ![]() и корреляционной матрицей
и корреляционной матрицей ![]() .
.
3). Корреляционные матрицы ![]() и
и ![]() обратимы (существуют матрицы
обратимы (существуют матрицы ![]() и
и ![]() ).
).
Для задачи лазерного многокомпонентного газоанализа трудно задать или отдать предпочтение какой-либо функции потерь. Поэтому оценку решения уравнения лазерного газоанализа будем определять из условия максимума апостериорной плотности вероятности ![]() .
.
При сделанных предположениях показано [4], что апостериорное распределение ![]() является нормальным и байесовская оценка
является нормальным и байесовская оценка ![]() вектора
вектора ![]() совпадает с оценкой, определяемой из максимума апостериорной плотности вероятности.
совпадает с оценкой, определяемой из максимума апостериорной плотности вероятности.
Тогда для задачи лазерного газоанализа (при использовании матричного уравнения (1)) байесовская оценка ![]() вектора
вектора ![]() определяется следующим уравнением
определяется следующим уравнением
![]() . (3)
. (3)
Здесь верхний индекс "Т" означает транспонирование матрицы, верхний индекс "-1" – обратную матрицу.
Матрица системы уравнений (1) размером положительно определена и для любого вектора измерения существует единственная байесовская оценка [4], которая дается выражением (3).
Байесовская оценка является несмещенной, эффективной и устойчивой (при уменьшении дисперсии шумов сходится в среднеквадратичном смысле к точному решению уравнения лазерного газоанализа).
Устойчивость полученного методом байесовской оценки решения достигается сужением класса возможных решений и это сужение основывается на вводимой (в решение) априорной информации об искомом решении - задается априорное нормальное распределение искомого решения и его первые два момента (среднее значение и корреляционная матрица). Такая априорная информация может быть вполне доступна во многих задачах, например, при рутинном газоанализе.
3. Проекционный метод
Исходным является уравнение (2), которое в другой форме записи имеет вид
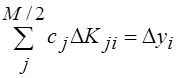 ,
, ![]() . (4)
. (4)
Величина ![]() является вектором в М/2 -мерном пространстве (K– число газов в смеси), а каждое из М/2 уравнений в (4) рассматривается как гиперплоскость.
является вектором в М/2 -мерном пространстве (K– число газов в смеси), а каждое из М/2 уравнений в (4) рассматривается как гиперплоскость.
Выберем для вектора концентраций газов ![]() начальное приближение -
начальное приближение - ![]() . Следующее приближение
. Следующее приближение ![]() находится как проекция
находится как проекция ![]() на первую гиперплоскость [9,10]
на первую гиперплоскость [9,10]
![]() , (5)
, (5)
где ![]() ; точкой обозначено скалярное произведение векторов.
; точкой обозначено скалярное произведение векторов.
Затем вычисляется проекция ![]() , используя формулу (5), векторы
, используя формулу (5), векторы ![]() и
и ![]() .
.
Далее вычисляется проекция ![]() и т.д. до проекции
и т.д. до проекции ![]() . На этом первый цикл итераций заканчивается. Далее проводится второй цикл итераций, который начинается с вектора
. На этом первый цикл итераций заканчивается. Далее проводится второй цикл итераций, который начинается с вектора ![]() и заканчивается вектором
и заканчивается вектором ![]() . После mитераций получим в качестве решения вектор
. После mитераций получим в качестве решения вектор ![]() .
.
Для задачи лазерного газоанализа многокомпонентных газовых смесей в качестве априорной информации может быть использовано среднее значение концентраций газов в качестве начального приближения ![]() .
.
4. Математическое моделирование
Для сравнительного анализа алгоритмов восстановления концентраций газов в сложных многокомпонентных смесях из многоспектральных лазерных измерений проводилось математическое моделирование.
Найденные (с использованием разных алгоритмов обработки) значения концентраций газов ![]() сравнивались с исходными (заданными) значениям концентраций
сравнивались с исходными (заданными) значениям концентраций ![]() и вычислялась погрешность определения концентраций газов
и вычислялась погрешность определения концентраций газов
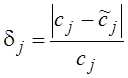 .
.
Математическое моделирование проводилось для одиночных измерений и серии из 1000 единичных измерений. Определялись концентрации газов и средние погрешности ![]() по серии из 1000 измерений.
по серии из 1000 измерений.
Результаты математического моделирования приведены на рисунках 1-10. На всех рисунках ряд 1 – метод прямого решения уравнения (1); ряд 2 – метод, основанный на построении байесовской оценки (3) (при построении байесовской оценки относительные среднеквадратические значения возможных изменений концентраций газов задавались равными 95 %); ряд 3 – проекционный метод, для которого в качестве начального приближения взят вектор со средними значениями концентраций газов. Средние значения концентраций газов отличались от заданных значений в большую или меньшую сторону на 80 %.
В практических задачах возникают ситуации, когда не только приближенные исходные данные, но и сама матрица коэффициентов поглощения ![]() известна не точно (в задаче газоанализа это соответствует, например, случаю, когда коэффициенты поглощения исследуемых газов известны с ошибками). Случайные ошибки в матрице коэффициентов поглощения (так же как и шум измерения) приводят к погрешностям определения концентраций газов.
известна не точно (в задаче газоанализа это соответствует, например, случаю, когда коэффициенты поглощения исследуемых газов известны с ошибками). Случайные ошибки в матрице коэффициентов поглощения (так же как и шум измерения) приводят к погрешностям определения концентраций газов.
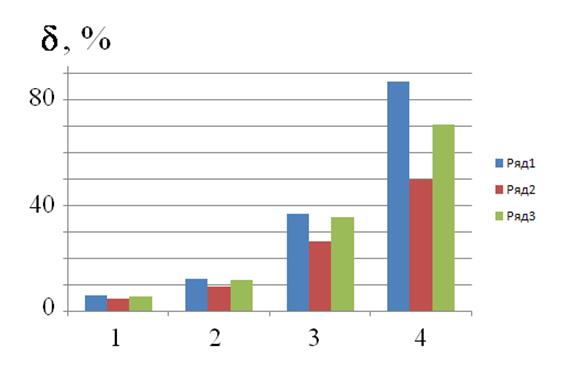
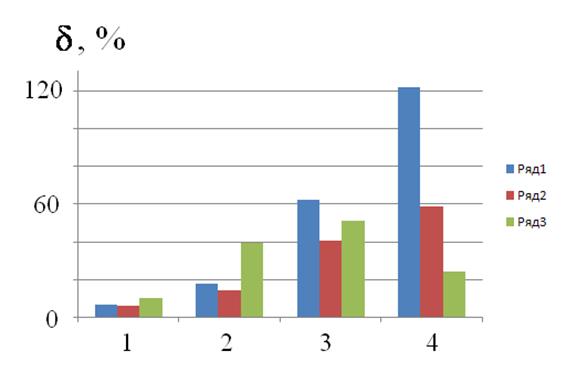
На рисунках 1, 2 приведены примеры результатов математического моделирования для шестикомпонентной смеси (этилен-фреон-12-гидразин-аммиак-метанол-этилакрилат) при неточно известной матрице коэффициентов поглощения газов (которая использовалась для восстановления по данным лазерных измерений концентраций газовых компонент смеси). Относительное среднеквадратическое значение шума измерения полагалось равным 3 %.
На рисунке 1 показаны погрешности ![]() (в процентах) определения концентрации гидразина, для которого в матрице коэффициентов поглощения
(в процентах) определения концентрации гидразина, для которого в матрице коэффициентов поглощения ![]() было введено искажение; на рисунке 2 - погрешности определения концентрации одного из других газов смеси (аммиака). На рисунках 1 и 2 введены обозначения: 1- неискаженная матрица коэффициентов поглощения газовых компонент; для 2-4 вместо
было введено искажение; на рисунке 2 - погрешности определения концентрации одного из других газов смеси (аммиака). На рисунках 1 и 2 введены обозначения: 1- неискаженная матрица коэффициентов поглощения газовых компонент; для 2-4 вместо ![]() в матрице коэффициентов поглощения стоят коэффициенты: 2 – 0,25
в матрице коэффициентов поглощения стоят коэффициенты: 2 – 0,25 ![]() ; 3 – 0,4
; 3 – 0,4 ![]() ; 4 – 0,55
; 4 – 0,55 ![]() . Для проекционного метода использовались пять итераций.
. Для проекционного метода использовались пять итераций.
Из рисунка 1 хорошо видно, что для метода прямого решения уравнения лазерного газоанализа с увеличением степени искажения матрицы коэффициентов поглощения газов погрешности определения концентрации гидразина сильно возрастают и становятся неприемлемо большими. Для байессовского и проекционного методов с увеличением степени искажения матрицы коэффициентов поглощения погрешности определения концентрации газов также возрастают, но гораздо медленнее. При этом погрешности для байессовского метода заметно меньше, чем для проекционного.
|
Рис. 1 - Зависимость погрешности определения концентрации гидразина от степени искажения матрицы коэффициентов поглощения газов |
Для других газов смеси ситуация похожая, однако, сам уровень погрешностей для всех методов обработки остается небольшим (рисунок 2).
|
Рис. 2 - Зависимость погрешности определения концентрации аммиака от степени искажения матрицы коэффициентов поглощения газов |
При математическом моделировании восстановления концентраций газов в смесях с компонентами без ярко выраженных максимумов в спектрах поглощения исследовались погрешности определения концентраций газовых компонент в шестикомпонентной смеси «этилен – фреон 12 – акролеин – аммиак – метанол – этилакрилат».
Для контроля количественного состава смеси были использованы следующие спектральные каналы измерения: 10P14, 10P10, 10R18, 10R22, 10P20, 10P22, 10R6, 10R12, 9P14, 9P22, 9R14, 9R22 (они соответствуют дискретно перестраиваемому по длине волны лазеру на углекислом газе [2]).
Показатели поглощения газовых компонент на длинах волн ![]() и
и ![]() приведены в Таблице 1.
приведены в Таблице 1.
Таблица 1
Показатели поглощения газовых компонент на длинах волн ![]() и
и ![]()
Газы | Этилен | Фреон 12 | Акролеин | ||||
Спектральные каналы |
|
|
|
|
|
| |
10P14 | 10P10 | 10R18 | 10R22 | 10P22 | 10P20 | ||
Коэффициенты поглощения | 32,14 | 3,09 | 9,15 | 0,93 | 1,75 | 1,41 | |
Газы | Аммиак | Метанол | Этилакрилат | ||||
Спектральные каналы |
|
|
|
|
|
| |
10R6 | 10R12 | 9P14 | 9P22 | 9R14 | 9R24 | ||
Коэффициенты поглощения | 32,5 | 0,06 | 9,75 | 3,65 | 7,02 | 4,02 | |
Из таблицы 1 видно, что исследуемая смесь содержит одну газовую компоненту (акролеин), которая не имеет ярко выраженного максимума поглощения при выбранных спектральных каналах измерения.
Примеры результатов математического моделирования приведены на рисунке 3 (для акролеина) и на рисунке 4 (для метанола).
Относительное среднеквадратическое значение шума измерения изменялось при математическом моделировании от 0,5 % до 8 % (шум измерения одинаковый во всех спектральных каналах). Для проекционного метода использовались три итерации. На рисунках 3 и 4: 1 соответствует среднеквадратическое значение шума измерения 0,5 %; 2 - 1 %; 3 – 2 %; 4 – 4 %; 5 – 8 %.
|
Рис. 3 - Погрешности определения концентрации акролеина, не имеющего ярко выраженного максимума поглощения для выбранных спектральных каналов |
|
Рис. 4 - Погрешности определения концентрации метанола в смеси с компонентой, не имеющей ярко выраженного максимума поглощения |
Из рисунков 3 и 4 видно, что с увеличением шума измерения погрешности определения концентрации газовых компонент стандартным методом решения (ряд 1), использующим обратную матрицу, увеличиваются. Причем, для компоненты, которая не имеет ярко выраженного максимума поглощения (акролеин), эта погрешность может достигать более 100 % (т.е. концентрация компоненты не определяется) уже при шуме 4 % (ряд 1 на рисунке 3). При использовании баессовского и проекционного методов погрешности определения концентраций газов существенно меньше. При этом погрешности для байессовский метод обеспечивает заметно меньшие погрешности, чем проекционный метод.
Примеры результатов математического моделирования восстановления концентраций газов в смесях с сильно отличающимися концентрациями газов приведены на рисунках 5 – 10. Здесь показаны погрешности определения концентраций газовых компонент в шестикомпонентной смеси «этилен – фреон 12 – гидразин – аммиак – метанол – этилакрилат». Были использованы следующие спектральные каналы измерения: 10P14, 10P10, 10R18, 10R22, 10P22, 10P28, 10R6, 10R12, 9P14, 9P20, 9R14, 9R22 [2]. Относительное среднеквадратическое значение шума измерения в уравнении (1) полагалось равным 5 % (шум измерения одинаковый во всех спектральных каналах). Для проекционного метода использовались 2 итерации. Исходные концентрации газов имеют примерно один порядок: 1,6 10![]() ; 2 – 4,6 10
; 2 – 4,6 10![]() ; 3 – 8 10
; 3 – 8 10![]() ; 4 – 8,5 10
; 4 – 8,5 10![]() ; 5 – 6,6 10
; 5 – 6,6 10![]() ; 6 – 9,2 10
; 6 – 9,2 10![]() .
.
На рисунке 5 приведены погрешности ![]() определения концентрации этилена при изменении его концентрации в смеси (концентрации остальных компонент соответствуют исходным).
определения концентрации этилена при изменении его концентрации в смеси (концентрации остальных компонент соответствуют исходным).
На рисунках 6 и 7 приведены погрешности ![]() определения концентрации соответственно фреона 12 и гидразина при изменении их концентрации в смеси (концентрации остальных компонент соответствуют исходным).
определения концентрации соответственно фреона 12 и гидразина при изменении их концентрации в смеси (концентрации остальных компонент соответствуют исходным).
|
Рис. 5 - Погрешности определения концентрации этилена. 1 соответствует концентрации 1,6 10 |
|
Рис. 6 - Погрешности определения концентрации фреона 12. 1 соответствует концентрации 4,6 10 |
|
Рис. 7 - Погрешности определения концентрации гидразина. 1 соответствует концентрации 8 10 |
На рисунке 8 приведены погрешности ![]() определения концентрации аммиака при изменении его концентрации (концентрации остальных газов соответствуют исходным).
определения концентрации аммиака при изменении его концентрации (концентрации остальных газов соответствуют исходным).
|
Рис. 8 - Погрешности определения концентрации аммиака. |
|
Рис. 9 - Погрешности определения концентрации этилена метанола. 1 соответствует концентрации 6,6 10 |
|
Рис. 10 - Погрешности определения концентрации этилакрилата. 1 соответствует концентрации 9,2 10 |
На рисунках 9 и 10 приведены погрешности ![]() определения концентрации соответственно метанола и этилакрилата при изменении их концентрации в смеси (концентрации остальных компонент соответствуют исходным).
определения концентрации соответственно метанола и этилакрилата при изменении их концентрации в смеси (концентрации остальных компонент соответствуют исходным).
Из рисунков 5-10 для всех газов смеси видно, что с уменьшением концентрации газовой компоненты погрешность ее определения стандартным методом решения (ряд 1 на рисунках 5-10), использующим обратную матрицу системы, увеличивается и может достигать сто процентов и более при уменьшении (на один или два порядка и более – в зависимости от газа) концентрации газовой компоненты по сравнению с исходной.
При использовании баессовского и проекционного методов (ряды 2 и 3 на рисунках 5-10) для определения концентрации газовой компоненты погрешность ее определения в существенно меньше (чем при использовании стандартного метода решения). В большинстве случаев наименьшие погрешности определения концентраций газов обеспечивает метод, основанный на построении байесовской оценки решения уравнения лазерного газоанализа.
Заключение
В статье проведен сравнительный анализ алгоритмов восстановления концентраций газов из многоспектральных лазерных измерений в сложных многокомпонентных смесях, в которых концентрации компонент газовой смеси отличаются на несколько порядков или присутствуют компоненты без ярко выраженных максимумов в спектрах поглощения. Показано, что использование метода, основанного на построении байесовской оценки решения уравнения лазерного газоанализа, в большинстве случаев обеспечивает наименьшие погрешности определения концентраций газов.
Список литературы
1. Козинцев В.И., Белов М.Л., Городничев В.А., Федотов Ю.В. Основы количественного лазерного анализа. М.: Из-во МГТУ им. Н.Э. Баумана, 2006. 464 c.
2. Козинцев В.И., Белов М.Л., Городничев В.А., Федотов Ю.В. Лазерный оптико-акустический анализ многокомпонентных газовых смесей. М.: Изд-во МГТУ им. Н.Э. Баумана, 2003. 352 с.
3. Оптико-электронные системы экологического мониторинга природной среды / В.И. Козинцев, В.М. Орлов, М.Л. Белов, В.А. Городничев, Б.В. Стрелков. М.: Изд-во МГТУ им. Н.Э. Баумана, 2002. 528 c.
4. Лазерная оптико-акустическая спектроскопия межмолекулярных взаимодействий в газах / Ю.Н. Пономарев, Б.Г. Агеев, М.В. Зигрист, В.А. Капитанов, Д. Куртуа, О.Ю. Никифорова. Томск: МГП «РАСКО», 2000. 200 с.
5. Пономарев Ю.Н. Лазерная оптико-акустическая спектроскопия атмосферы // Оптика атмосферы и океана. 1995. Т. 8, № 1-2. С. 224-241.
6. Лазерная аналитическая спектроскопия / В.С. Антонов, Г.И. Беков, М.А. Большов, В.П. Жаров, В.С. Летохов, Ю.А. Курицын, Р.И. Персонов, А.Н. Шибанов. М.: Наука, 1986.320 с.
7. Белов М.Л., Добрица Д.Б., Козинцев В.И., Городничев В.А. Восстановление концентраций компонент газовых смесей из многоспектральных лазерных измерений методом статистической регуляризации // Вестник МГТУ им. Н.Э. Баумана. Сер. Приборостроение. 2001. № 3. С. 36-43.
8. Белов М.Л., Городничев В.А., Козинцев В.И., Федотов Ю.В. Метод поиска квазирешений в задаче лазерного оптико-акустического газоанализа // Оптика атмосферы и океана. 2002. Т. 15, № 4. С. 388-392.
9. Еременко Л.Н., Козинцев В.И., Городничев В.А. Метод байесовских оценок в задаче лазерного газоанализа // Известия вузов. Физика. 2008. № 9. С. 29-35.
10. Козинцев В.И., Иден Г., Белов М.Л., Смирнова О.А., Городничев В.А., Еременко Л.Н., Федотов Ю.В. Определение концентраций газов в сложных многокомпонентных смесях методом байесовских оценок // Вестник МГТУ им. Н.Э. Баумана. Сер. Приборостроение. 2009. № 4. С. 1-13.
11. Городничев В.А., Белов М.Л., Бусаргин А.Ю., Еременко Л.Н. Лазерный анализ многокомпонентных смесей газов с сильно отличающимися концентрациями // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2013. № 2. DOI: 10.7463/0213.0539070
12. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. 288 с.
13. Воскобойников Ю.Э., Преображенский Н.Г., Седельников А.Н. Математическая обработка эксперимента в молекулярной газодинамике. Новосибирск: Наука, 1984. 238 с.
14. Макушкин Ю.С., Мицель А.А., Хмельницкий Г.С. Лазерная абсорбционная диагностика атмосферных газов // Журнал прикладной спектроскопии. 1981. Т. 35, вып. 5. С. 785-790.
15. Козинцев В.И. Об обработке сигналов лазерного оптико-акустического газоанализатора при анализе многокомпонентных газовых смесей // Оптика атмосферы и океана. 1996. Т. 9, № 10. С. 1373-1378.
16. Авдиенко В.В., Белов М.Л., Городничев В.А., Добрица Д.Б., Козинцев В.И. Мониторинг многокомпонентных газовых смесей с помощью лазерного оптико-акустического полигазоанализатора // Журнал прикладной спектроскопии. 1996. Т. 65, № 5. С. 755-759.
17. Белов М.Л., Добрица Д.Б., Городничев В.А., Козинцев В.И. Сравнительный анализ методов восстановления концентраций газов в многокомпонентных смесях из данных измерений лазерного оптико-акустического газоанализатора // Оптика атмосферы и океана. 2000. Т. 13, № 2. С. 146-150.
Публикации с ключевыми словами: лазер, байесовская оценка, проекционный метод, количественный газоанализ, сложные многокомпонентные газовые смеси
Публикации со словами: лазер, байесовская оценка, проекционный метод, количественный газоанализ, сложные многокомпонентные газовые смеси
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||