научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2013
DOI: 10.7463/0813.0605972
УДК 623.454.255
МГТУ им. Н.Э. Баумана, Москва, Российская федерация
Введение
При исследовании функционирования контактных датчиков цели (КДЦ) взрывателей необходимо количественно описывать силы инерции, порождаемые взаимодействием боеприпаса с преградами различного типа. При этом применяют эмпирические формулы, т.е. экспериментально полученные соотношения, которые связывают характеристики боеприпаса (масса qи калибр d), скорость встречи ![]() с преградой и ее физико-механические свойства. В фундаментальных работах [1, 2] рассмотрены теоретические аспекты процесса взаимодействия боеприпасов с преградами различного типа. Известны специальные прикладные программы, позволяющие проследить развитие во времени пространственного процесса внедрения боеприпаса в преграду [3].
с преградой и ее физико-механические свойства. В фундаментальных работах [1, 2] рассмотрены теоретические аспекты процесса взаимодействия боеприпасов с преградами различного типа. Известны специальные прикладные программы, позволяющие проследить развитие во времени пространственного процесса внедрения боеприпаса в преграду [3].
Различают следующие виды взаимодействия боеприпаса с преградами [2]: мгновенно-контактное (взрыв боевого заряда происходит в результате срабатывания КДЦ мгновенного действия, а энергия взрыва расходуется на разрушение объектов на поверхности преграды) и ударно-проникающее (удар боеприпаса о преграду и внедрение в нее на заданную или полную глубину, соответствующую остановке боеприпаса; взрыв боевого заряда происходит в результате срабатывания инерционного КДЦ). Движение боеприпаса в преграде, на которое не влияют ее размеры, называют прониканием, а движение, связанное с разрушением тыльных слоев преграды и выходом боеприпаса, – пробиванием.
Одной из теоретических предпосылок при установлении закона сопротивления сплошной среды является следующее положение – кинетическая энергия боеприпаса ![]() расходуется исключительно на преодоление сопротивления преграды. Данное положение тем ближе к истине, чем податливее преграда, прочнее снаряд и меньше скорость встречи. Выходной сигнал КДЦ (механический или электрический) представляет собой отклик чувствительного элемента (сенсора) на динамическое взаимодействие головной части боеприпаса с целью, при этом возникают волны механического напряжения, причем наиболее энергоемки продольные волны [4].
расходуется исключительно на преодоление сопротивления преграды. Данное положение тем ближе к истине, чем податливее преграда, прочнее снаряд и меньше скорость встречи. Выходной сигнал КДЦ (механический или электрический) представляет собой отклик чувствительного элемента (сенсора) на динамическое взаимодействие головной части боеприпаса с целью, при этом возникают волны механического напряжения, причем наиболее энергоемки продольные волны [4].
Процесс проникания боеприпаса в сплошные среды обычно разбивают на три этапа [5, 6].
1) Внедрение боеприпаса на глубину, примерно равную длине головной части L. Этот этап характеризуется изменением площади контакта со средой и возрастанием силы сопротивления до максимума, падение скорости боеприпаса относительно невелико.
2) Площадь контакта боеприпаса со средой практически постоянна, однако скорость все время уменьшается, в связи с чем сила сопротивления преграды также непрерывно снижается. За боеприпасом образуется канал (каверна), который в средах малой прочности схлопывается.
3) Сквозное прибивание – данный этап возможен при конечной толщине преграды и достаточно большой скорости снаряда (бронебойного или бетонобойного).
Первым этапом внедрения часто пренебрегают, ограничиваясь рассмотрением только стационарного движения боеприпаса во время второго этапа и считая, что он определяет все основные закономерности процесса [6]. Однако с точки зрения функционирования КДЦ взрывателя начальный этап является основным, поскольку срабатывание КДЦ должно произойти в пределах именно этого этапа (т.е. в пределах длительности переднего фронта закона ударной перегрузки).
Параметры данного этапа внедрения боеприпаса могут быть выявлены на основе соответствующей аппроксимации начального участка силовой характеристики преграды. В настоящей работе предложены два способа аппроксимации, основанные на использовании эмпирических формул для полного пути внедрения боеприпаса, с учетом экспериментально установленных фактов, указанных выше. При этом сделано предположение, что влияние скорости и перемещения боеприпаса при внедрении может быть учтено раздельно, путем введения в силовую характеристику преграды соответствующих функциональных множителей.
Задача решается в одномерной постановке, т.е. траектория боеприпаса в преграде считается прямолинейной. Такое допущение, строго говоря, приемлемо в случае преград типа грунта, в ограниченном диапазоне значений угла встречи от нормали к поверхности преграды (до 20…300). Однако, поскольку объектом исследования являются параметры только начального этапа внедрения, влиянием последующего искривления траектории боеприпаса, при бóльших углах встречи, с практической точки зрения можно пренебречь
Показано, что предлагаемый подход, будучи приближенным, тем не менее дает приемлемое для практики описание процесса взаимодействия боеприпаса с преградой. В качестве примера приведены результаты расчета КДЦ кассетного боевого элемента, причем получаемое расчетное значение перегрузки совпадает с рабочим уровнем, указанным в техническом задании.
Рассмотрен вопрос о возможности создания КДЦ интеграторного типа как средства определения запреградной скорости боеприпаса и фильтрации колебательных составляющих выходного сигнала КДЦ..
1 Эмпирические формулы
Силовая характеристика преграды при одномерной постановке задачи может быть представлена следующим образом:
| (1) |
Здесь Р – сила сопротивления; X и V – перемещение и скорость боеприпаса, соответственно, причем взаимосвязь ![]() определяет динамику процесса и в большой степени зависит от начальной скорости удара
определяет динамику процесса и в большой степени зависит от начальной скорости удара ![]() . Если эта взаимосвязь известна, то, очевидно, можно считать, что
. Если эта взаимосвязь известна, то, очевидно, можно считать, что ![]() .
.
Широко известно описание силовой характеристики в форме, предложенной Г.И. Покровским [2, 5, 6]
| (2) |
где эмпирические коэффициенты а, bи с характеризуют, соответственно, динамические, вязкие и прочностные свойства преграды; ![]() – коэффициент, учитывающий конфигурацию головной части снаряда;
– коэффициент, учитывающий конфигурацию головной части снаряда; ![]() – площадь его миделевого сечения. При таком описании сила сопротивления максимальна в начальный момент удара, когда
– площадь его миделевого сечения. При таком описании сила сопротивления максимальна в начальный момент удара, когда ![]() , т.е.
, т.е. ![]() ; при последующем движении боеприпаса скорость и, соответственно, сила сопротивления уменьшаются и при проникании боеприпаса на полную глубину
; при последующем движении боеприпаса скорость и, соответственно, сила сопротивления уменьшаются и при проникании боеприпаса на полную глубину ![]() обращаются в ноль.
обращаются в ноль.
Уравнение прямолинейногодвижения боеприпаса (рассматриваемого как твердое тело) в процессе взаимодействия его с преградой можно записать следующим образом:
| (3) |
При расчете КДЦ удобно оперировать перегрузкой
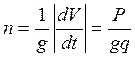
Интегрируя (3), будем иметь
 .
.
Принимая ![]() (остановка боеприпаса), получаем соотношение
(остановка боеприпаса), получаем соотношение
| (4) |
т.е. кинетическая энергия боеприпаса затрачивается на совершение работы, связанной с преодолением сопротивления среды, о чем сказано выше. Схема проникания снаряда в преграду при прямолинейной траектории показана на рисунке 1, где ![]() – глубина проникания;
– глубина проникания; ![]() и
и ![]() – углы встречи от нормали и относительно поверхности преграды соответственно.
– углы встречи от нормали и относительно поверхности преграды соответственно.
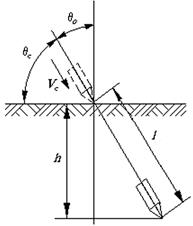
Рисунок 1 – Схема проникания снаряда в преграду
Эмпирические формулы, которые обычно используют для определения ![]() , выводят из выражения (2), удерживая в нем те или иные члены, которые характеризуют доминирующие физические свойства преграды. Наиболее известные из них представлены в таблице 1.
, выводят из выражения (2), удерживая в нем те или иные члены, которые характеризуют доминирующие физические свойства преграды. Наиболее известные из них представлены в таблице 1.
Таблица 1 – Эмпирические формулы для определения ![]()
Название формулы | Выражение для | Примечание |
Березанская |
|
|
Забудского-Маиевского |
| |
Вуича |
| m – поправочный коэффициент для трех классов преград: грунт, кладка, дерево; корректировка параметров: |
Петри |
|
|
Числовые значения коэффициентов, фигурирующих в этих формулах, можно найти в ряде работ [5–9].
2 Аппроксимация силовой характеристики преграды
При конструировании выражения для силовой характеристики преграды следует принять во внимание следующие экспериментально установленные факты:
1) при внедрении боеприпаса на длину головной части L сила сопротивления преграды, как сказано выше, максимальна;
2) при внедрении боеприпаса, равном полному пути ![]() , сила сопротивления и скорость снаряда обращаются в ноль.
, сила сопротивления и скорость снаряда обращаются в ноль.
Возможность выявления параметров переднего фронта закона перегрузки на основе использования ![]() можно обосновать следующим образом. Значения
можно обосновать следующим образом. Значения ![]() , подсчитываемые по эмпирическим формулам, получены в результате обработки результатов полигонных стрельб и, следовательно, интегрально учитывают весь ход протекания ударного процесса при взаимодействии боеприпаса с преградой, в том числе (что особенно важно подчеркнуть) и первый этап внедрения. Иначе говоря, параметры первого этапа как бы «зашифрованы» в величине
, подсчитываемые по эмпирическим формулам, получены в результате обработки результатов полигонных стрельб и, следовательно, интегрально учитывают весь ход протекания ударного процесса при взаимодействии боеприпаса с преградой, в том числе (что особенно важно подчеркнуть) и первый этап внедрения. Иначе говоря, параметры первого этапа как бы «зашифрованы» в величине ![]() , и их необходимо извлечь.
, и их необходимо извлечь.
2.1 Кусочно-линейная аппроксимация
Рассмотрим два способа приближенного описания силовой характеристики. Предположим сначала, что она в пределах всего пути внедрения может быть представлена в виде кусочно-линейной функции перемещения снаряда:
| (5) |
Более строгая зависимость ![]() может быть в принципе выведена из формулы (1), если известна взаимосвязь между элементами движения боеприпаса
может быть в принципе выведена из формулы (1), если известна взаимосвязь между элементами движения боеприпаса ![]() , как отмечено выше. Однако с практической точки зрения достаточно того, что выражение (5) отображает два важных факта: сила сопротивления преграды максимальна при внедрении боеприпаса на длину головной части и обращается в ноль при внедрении на полную глубину. Величина максимальной силы сопротивления
, как отмечено выше. Однако с практической точки зрения достаточно того, что выражение (5) отображает два важных факта: сила сопротивления преграды максимальна при внедрении боеприпаса на длину головной части и обращается в ноль при внедрении на полную глубину. Величина максимальной силы сопротивления ![]() априорно неизвестна, но может быть найдена с помощью энергетического соотношения (4), из которого следует, что кинетическая энергия удара равна площади под силовой характеристикой в пределах полного пути внедрения l, т.е.
априорно неизвестна, но может быть найдена с помощью энергетического соотношения (4), из которого следует, что кинетическая энергия удара равна площади под силовой характеристикой в пределах полного пути внедрения l, т.е.
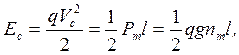
откуда

и, соответственно, максимальная перегрузка
| (6) |
Отсюда видно, что чем больше ![]() , т.е. чем более податлива преграда, тем (при одинаковой скорости встречи) ниже уровень перегрузки, что вполне очевидно с физической точки зрения. Аналогичный результат получен в работе [9], однако авторы, используя энергетическое соотношение (4), участком нарастания силы сопротивления до максимума пренебрегают, т.е. считают, что (в наших обозначениях)
, т.е. чем более податлива преграда, тем (при одинаковой скорости встречи) ниже уровень перегрузки, что вполне очевидно с физической точки зрения. Аналогичный результат получен в работе [9], однако авторы, используя энергетическое соотношение (4), участком нарастания силы сопротивления до максимума пренебрегают, т.е. считают, что (в наших обозначениях)
 .
.
Здесь «по умолчанию» предполагается, что сила сопротивления максимальна в момент встречи боеприпаса с преградой, как это следует из формулы (2).
Запишем для первого этапа уравнение (3), учитывая (5):
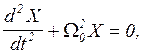 .
.
Здесь ![]() Решение данного уравнения имеет вид
Решение данного уравнения имеет вид
 .
.
Принимая ![]() , найдем длительность переднего фронта
, найдем длительность переднего фронта
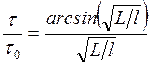 .
.
Здесь ![]() – время свободного перемещения боеприпаса на длину головной части (если пренебрегать сопротивлением преграды, т.е. падением скорости в пределах переднего фронта). Влияние энергии удара и свойств преграды характеризуется множителем, зависящим от отношения
– время свободного перемещения боеприпаса на длину головной части (если пренебрегать сопротивлением преграды, т.е. падением скорости в пределах переднего фронта). Влияние энергии удара и свойств преграды характеризуется множителем, зависящим от отношения ![]() . Скорость боеприпаса в конце первого этапа внедрения
. Скорость боеприпаса в конце первого этапа внедрения
 .
.
Наконец, находим закон перегрузки
 .
.
Из приведенных формул видно, что по мере возрастания энергии удара (т.е. увеличения l) относительная доля начального этапа удара уменьшается.
2.2 Учет изменения площади взаимодействия с преградой
Теперь предположим, что влияние элементов движения боеприпаса на силовую характеристику преграды можно учитывать раздельно, записав выражение (1) в виде произведения двух функциональных множителей:
| (7) |
где ![]() – относительное перемещение боеприпаса на начальном этапе (
– относительное перемещение боеприпаса на начальном этапе (![]() ). Функция
). Функция ![]() характеризует относительное изменение площади сечения при возрастании силы сопротивления до максимума во время первого этапа внедрения, причем
характеризует относительное изменение площади сечения при возрастании силы сопротивления до максимума во время первого этапа внедрения, причем ![]() . Функция
. Функция ![]() отображает квазистационарный (установившийся) процесс внедрения во время второго этапа, который описывается формулой (7) при
отображает квазистационарный (установившийся) процесс внедрения во время второго этапа, который описывается формулой (7) при ![]() :
:
![]() .
.
Введем безразмерные скорость боеприпаса ![]() и текущее время
и текущее время ![]() . Тогда
. Тогда
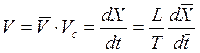 ,
,
а величину Tопределим из условия ![]() . В результате уравнение движения боеприпаса можно записать в следующем виде:
. В результате уравнение движения боеприпаса можно записать в следующем виде:
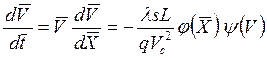 .
.
Рассмотрим в качестве примера Березанскую формулу, которая выводится с помощью (2) при учете только вязкой составляющей, т.е. принимаем
![]() .
.
Нетрудно видеть, что (см. таблицу 1)
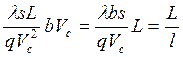 .
.
Таким образом,
 ..
..
и, соответственно,
 ,
,
где  – скорость в конце переднего фронта закона перегрузки. Зависимость
– скорость в конце переднего фронта закона перегрузки. Зависимость ![]() может быть вычислена из соотношений
может быть вычислена из соотношений
 ,
,
Длительность переднего фронта
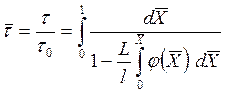 .
.
Если, например, считать, что головная часть коническая, то ![]() , и тогда
, и тогда
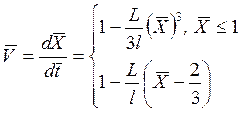 .
.
Соответственно,
 ,
,
где ![]() . Принимая
. Принимая ![]() , найдем длительность переднего фронта
, найдем длительность переднего фронта
 .
.
3 Расчет КДЦ кассетного боевого элемента
Инерционный КДЦ простейшего типа состоит из ударника массой m, контрпредохранительной пружины с жесткостью с и капсюля-воспламенителя (или капсюля-детонатора). Уравнения движения боеприпаса и ударника при встрече с преградой имеют вид
 ,
,
где ![]() – начальное сопротивление пружины; с – ее жесткость;
– начальное сопротивление пружины; с – ее жесткость; ![]() – скорость ударника. Введя перегрузку боеприпаса, уравнение движения ударника можно записать в виде
– скорость ударника. Введя перегрузку боеприпаса, уравнение движения ударника можно записать в виде
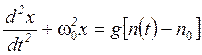 ,
,
где ![]() – начальная «настройка» КДЦ;
– начальная «настройка» КДЦ; ![]() – условная частота собственных колебаний. Полная система уравнений, необходимая для численного решения данной задачи, будет иметь вид
– условная частота собственных колебаний. Полная система уравнений, необходимая для численного решения данной задачи, будет иметь вид
 .
.
Движение ударника начнется в момент времени ![]() , определяемый из условия
, определяемый из условия ![]() . Соответствующее заглубление боеприпаса
. Соответствующее заглубление боеприпаса ![]() , очевидно, тем больше, чем больше
, очевидно, тем больше, чем больше ![]() . Следует отметить, что величина
. Следует отметить, что величина ![]() в данном случае имеет чисто расчетный смысл, поскольку срабатывание КДЦ произойдет при заглублении боеприпаса, соизмеримом с длиной головной части. Условие надежности действия КДЦ
в данном случае имеет чисто расчетный смысл, поскольку срабатывание КДЦ произойдет при заглублении боеприпаса, соизмеримом с длиной головной части. Условие надежности действия КДЦ
![]() ,
,
где ![]() – скорость ударника в момент накола; a – расстояние между жалом ударника и капсюлем;
– скорость ударника в момент накола; a – расстояние между жалом ударника и капсюлем; ![]() – минимальная скорость, обеспечивающая 100%-ное срабатывание капсюля.
– минимальная скорость, обеспечивающая 100%-ное срабатывание капсюля.
Рассмотрим конкретный пример [10]: боеприпас – кассетный боевой элемент (КБЭ), представление о конструкции которого дает рисунок 2 [5]. Параметры изделия таковы ![]() м;
м; ![]() кг; длина головной части
кг; длина головной части ![]() м; расчетная (целевая) преграда – грунт средней плотности; скорость встречи с преградой от 90 до 200 м/с; угол встречи
м; расчетная (целевая) преграда – грунт средней плотности; скорость встречи с преградой от 90 до 200 м/с; угол встречи ![]() , т.е. траекторию КБЭ в преграде можно считать прямолинейной и использовать приведенные выше соотношения для этого случая.
, т.е. траекторию КБЭ в преграде можно считать прямолинейной и использовать приведенные выше соотношения для этого случая.

1 – взрыватель, 2 – блок готовых поражающих элементов, 3 – разрывной заряд, 4 – стабилизатор
Рисунок 2 – Кассетный боевой элемент
Параметры инерционного КДЦ, входящего в состав взрывателя к КБЭ: масса ударника ![]() г (
г (![]() м/с); жесткость упругого контрпредохранителя
м/с); жесткость упругого контрпредохранителя ![]() H/м; начальная осадка
H/м; начальная осадка ![]() мм;
мм; ![]() мм. Для расчета полного пути КБЭ в преграде воспользуемся Березанской формулой. Принимаем значение коэффициента преграды (грунт средней плотности)
мм. Для расчета полного пути КБЭ в преграде воспользуемся Березанской формулой. Принимаем значение коэффициента преграды (грунт средней плотности) ![]() [6], коэффициент формы
[6], коэффициент формы ![]() . Тогда
. Тогда
 ;
; 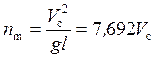
Сначала используем кусочно-линейную аппроксимацию силовой характеристики, согласно (5):

Основные параметры ударного процесса приведены в таблице 3. Отметим, что эти параметры достаточно близки к указанным в техническом задании на КБЭ – расчетный уровень перегрузки при скорости встречи около 120 м/с задан равным 1000.
Таблица 3 – Параметры ударного процесса при встрече КБЭ с преградой
| l, м |
| t, мс |
|
|
90 100 110 120 130 140 150 160 170 180 190 200 | 1,194 1,326 1,459 1,592 1,724 1,857 1,990 2,122 2,255 2,388 2,520 2,653 | 692 768 845 922 1000 1076 1152 1229 1306 1383 1460 1536 | 2,408 2,160 1,958 1,791 1,650 1,530 1,426 1,335 1,255 1,184 1,121 1,064 | 1,032 1,028 1,026 1,023 1,022 1,020 1,018 1,017 1,016 1,015 1,014 1,013 | 0,907 0,917 0,925 0,931 0,937 0,941 0,945 0,949 0,952 0,955 0,957 0,959 |
В таблице 4 даны результаты исследования функционирования КДЦ в указанных условиях нагружения, через ![]() обозначено время срабатывания (от момента начала контакта). Видно, что срабатывание КДЦ в данном случае происходит на спадающем участке кривой перегрузки (
обозначено время срабатывания (от момента начала контакта). Видно, что срабатывание КДЦ в данном случае происходит на спадающем участке кривой перегрузки (![]() ), хотя и на небольшом удалении от максимума.
), хотя и на небольшом удалении от максимума.
Таблица 4 – Параметры срабатывания КДЦ
|
|
|
|
|
90 100 110 120 130 140 150 160 170 180 190 200 | 2,450 2,283 2,142 2,021 1,916 1,824 1,743 1,670 1,606 1,546 1,493 1,443 | 1,018 1,057 1,094 1,129 1,161 1,192 1,222 1,251 1,279 1,305 1,332 1,356 | 8,470 9,075 9,633 10,16 10,67 11,14 11,59 12,03 12,46 12,86 13,27 13,64 | 1,098 1,177 1,249 1,318 1,383 1,444 1,503 1,560 1,616 1,667 1,720 1,768 |
В случае более прочной преграды при одинаковой скорости встречи длительность переднего фронта практически не изменяется (она имеет порядок ![]() ), но возрастает пиковый уровень перегрузки, т.е. увеличивается энергоемкость начального участка кривой перегрузки. Поэтому срабатывание КДЦ будет происходить в пределах длительности переднего фронта.
), но возрастает пиковый уровень перегрузки, т.е. увеличивается энергоемкость начального участка кривой перегрузки. Поэтому срабатывание КДЦ будет происходить в пределах длительности переднего фронта.
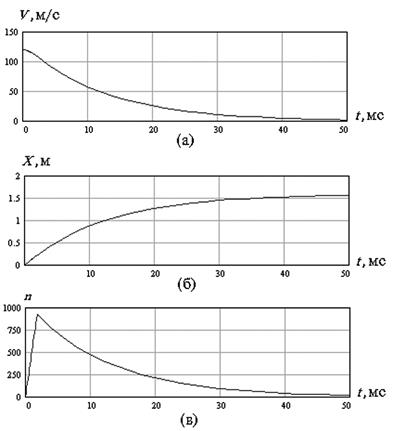
(а) – скорость; (б) – перемещение; (в) – закон перегрузки
Рисунок 3 – Элементы движения КБЭ при встрече с преградой
На рисунке 3 показаны элементы движения КБЭ при указанной в ТЗ скорости встречи с преградой ![]() м/с. Расчетный уровень перегрузки соответствует указанному в ТЗ (порядка 1000). Следует отметить, что закон перегрузки в пределах переднего фронта практически линейный, т.е. соответствует принятой аппроксимации (вследствие относительно малого падения скорости). Этот факт может быть использован при приближенном описании закона перегрузки в пределах переднего фронта, например, при оценке чувствительности КДЦ и оптимизации его параметров [10].
м/с. Расчетный уровень перегрузки соответствует указанному в ТЗ (порядка 1000). Следует отметить, что закон перегрузки в пределах переднего фронта практически линейный, т.е. соответствует принятой аппроксимации (вследствие относительно малого падения скорости). Этот факт может быть использован при приближенном описании закона перегрузки в пределах переднего фронта, например, при оценке чувствительности КДЦ и оптимизации его параметров [10].
На рисунке 4 приведены элементы движения ударника КДЦ, а также, для сравнения, начальный участок кривой перегрузки. В целом результаты проведенного расчета свидетельствуют, что в заданных условиях встречи КБЭ с целевой преградой надежное срабатывание КДЦ гарантируется. Таким образом, предложенный подход позволяет получить вполне адекватную оценку работоспособности инерционного КДЦ, по крайней мере при взаимодействии боеприпаса с преградой рассматриваемого типа.
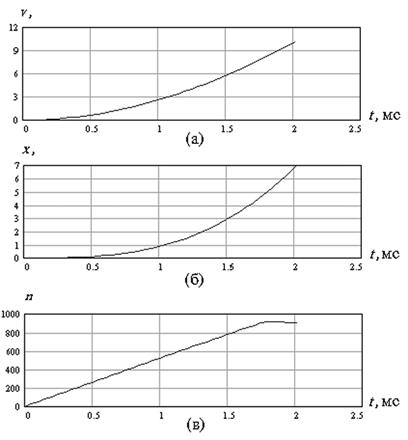
(а) – скорость ударника; (б) – перемещение ударника; (в) – начальный участок закона перегрузки
Рисунок 4 – Элементы движения ударника КДЦ
Выше (раздел 2.2) приведены соотношения, получающиеся при применении Березанской формулы, в частности, при конической головной части боеприпаса. Для рассматриваемого КБЭ (при ![]() м/с) имеем:
м/с) имеем: ![]() м;
м; ![]() м;
м; ![]() с. На рисунках 5 и 6 показаны результаты моделирования процесса взаимодействия боеприпаса с преградой. Сравнивая эти графики с полученными выше (рисунок 3), отметим близость основных параметров, что подтверждает принципиальную приемлемость обоих подходов.
с. На рисунках 5 и 6 показаны результаты моделирования процесса взаимодействия боеприпаса с преградой. Сравнивая эти графики с полученными выше (рисунок 3), отметим близость основных параметров, что подтверждает принципиальную приемлемость обоих подходов.
Задача рассматривалась в упрощенной, т.е. одномерной постановке, но вновь подчеркнем, что влиянием искривления траектории боеприпаса в преграде можно, по-видимому, пренебречь, поскольку оценивается работоспособность КДЦ только в пределах начального этапа внедрения.

Рисунок 5 – Закон и передний фронт перегрузки при встрече КБЭ с преградой
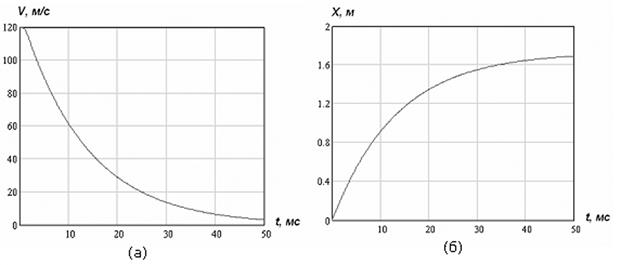
а – скорость; б – заглубление
Рисунок 6 – Элементы движения КБЭ
4 Интегрирующий КДЦ
Интегрирование выходного сигнала КДЦ может быть использовано для получения информации о скорости боеприпаса при пробитии преграды, т.е. для фиксации момента выхода боеприпаса в запреградное пространство, поскольку при этом скорость становится практически постоянной. При интегрировании происходит сглаживание пульсаций (и, следовательно, волновых наложений), и можно получить достаточно гладкий сигнал, поддающийся более эффективной обработке.
Как известно, при измерении быстропротекающих процессов стремятся использовать высокочастотные измерительные средства [11–13]. Это нетрудно объяснить, предположив, что уравнение, описывающее преобразование воздействия ![]() в отклик датчика
в отклик датчика ![]() , может быть записано в виде
, может быть записано в виде
| (8) |
где k– масштабный коэффициент; ![]() – частота собственных колебаний; h – коэффициент демпфирования. Если из (8) выразить закон реакции, то получим соотношение
– частота собственных колебаний; h – коэффициент демпфирования. Если из (8) выразить закон реакции, то получим соотношение
| (9) |
в котором ![]() – основная, или «статическая», компонента отклика, пропорциональная закону входного воздействия, а
– основная, или «статическая», компонента отклика, пропорциональная закону входного воздействия, а ![]() – динамическая ошибка измерения, т.е. компонента, зависящая от частоты собственных колебаний и «маскирующая» основную составляющую. Из (9) видно, что точность измерения тем выше, чем больше член
– динамическая ошибка измерения, т.е. компонента, зависящая от частоты собственных колебаний и «маскирующая» основную составляющую. Из (9) видно, что точность измерения тем выше, чем больше член ![]() по сравнению с остальными двумя членами в левой части. Следует, однако, отметить, что при этом также снижается и чувствительность преобразователя, поскольку «статическая» компонента обратно пропорциональна
по сравнению с остальными двумя членами в левой части. Следует, однако, отметить, что при этом также снижается и чувствительность преобразователя, поскольку «статическая» компонента обратно пропорциональна ![]() . Условия, при выполнении которых обеспечивается требуемая точность измерения динамических процессов, сформулированы в известных работах академика А.Н. Крылова, например, [14].
. Условия, при выполнении которых обеспечивается требуемая точность измерения динамических процессов, сформулированы в известных работах академика А.Н. Крылова, например, [14].
При функционировании КДЦ выходной сигнал, помимо основной (информативной) составляющей, будет содержать паразитные компоненты (обусловленные распространением упругих волн по корпусу и блокам бортового оборудования), которые необходимо «отфильтровать». Это особенно относится к ракетам, имеющим большие продольные размеры. Фильтрация, естественно, может быть реализована и с помощью системы обработки, но представляет интерес оценка возможности простейшего варианта, т.е. использования самого сенсора как интегратора.
Помимо «фильтрации», т.е. сглаживания выходного сигнала, интегрирование может быть и рабочим, т.е. основным преобразованием. Например, может быть использован такой информативный признак цели, как падение (изменение) скорости боеприпаса при взаимодействии с преградой (такая ситуация характерна, например, для противокорабельной ракеты, пробивающей борт корабля или стенку берегового укрепления).
Если в левой части уравнения (8) доминирующим будет «диссипативный» член, т.е. демпфирующий элемент, сила сопротивления которого пропорциональна относительной скорости, то
| (10) |
т.е. основной будет компонента ![]() , пропорциональная интегралу от входного воздействия, а
, пропорциональная интегралу от входного воздействия, а ![]() в данном случае – ошибка интегрирования. Из структуры динамической ошибки следует, что необходимо стремиться к уменьшению частоты собственных колебаний, т.е. преобразователь должен обладать большой инерционностью, что может быть достигнуто, например, за счет ослабления опоры сенсора. Кроме того, поскольку в состав ошибки входит производная отклика
в данном случае – ошибка интегрирования. Из структуры динамической ошибки следует, что необходимо стремиться к уменьшению частоты собственных колебаний, т.е. преобразователь должен обладать большой инерционностью, что может быть достигнуто, например, за счет ослабления опоры сенсора. Кроме того, поскольку в состав ошибки входит производная отклика ![]() , то он должен представлять собой относительно медленно изменяющийся во времени процесс.
, то он должен представлять собой относительно медленно изменяющийся во времени процесс.
Для дальнейшего анализа воспользуемся спектральным (частотным) подходом. Согласно (8), передаточная функция преобразователя имеет вид
| (11) |
где s– оператор Лапласа. Соответственно, комплексный коэффициент передачи

и амплитудно-частотная характеристика (АЧХ)
| (12) |
где ![]() ;
; ![]() – коэффициент демпфирования. При
– коэффициент демпфирования. При ![]() имеем «статическое» значение частотной характеристики, т.е.
имеем «статическое» значение частотной характеристики, т.е. ![]() .
.
Для идеального интегратора, согласно (11),
| (13) |
Нормируя частотные характеристики (13) и (11) по ![]() , получим
, получим
| (14) |
| (15) |
Сравнивая (14) и (15), нетрудно заметить, что близость частотных характеристик «реальной» и идеальной интегрирующей систем обеспечивается в сравнительно узком диапазоне частот, в пределах которого ![]() , или отношение
, или отношение ![]() достаточно мало. На рисунках 7 и 8 показаны АЧХ, соответствующие выражениям (14) (кривая 1) и (15) (кривая 2) при различных значениях e. Наглядно видно, что по мере увеличения значения e система постепенно утрачивает колебательные свойства и приближается к апериодической.
достаточно мало. На рисунках 7 и 8 показаны АЧХ, соответствующие выражениям (14) (кривая 1) и (15) (кривая 2) при различных значениях e. Наглядно видно, что по мере увеличения значения e система постепенно утрачивает колебательные свойства и приближается к апериодической.
.

Рисунок 7 – АЧХ при |
| Рисунок 8 – АЧХ при |
Исходное уравнение преобразователя (8) приведем к безразмерному виду, введя следующие величины: статическое смещение ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() – коэффициент демпфирования. В результате получим
– коэффициент демпфирования. В результате получим
| (16) |
Такая запись уравнения упрощает исследование, поскольку необходимо задать только форму (и временные параметры) внешнего воздействия, т.е. закон ![]() и варьировать значения коэффициента демпфирования. На рисунках 9 и 10 показаны закон в виде последовательности двух прямоугольных импульсов противоположного знака и результат точного интегрирования, соответственно, а на рисунке 11 – сигнал на выходе преобразователя (
и варьировать значения коэффициента демпфирования. На рисунках 9 и 10 показаны закон в виде последовательности двух прямоугольных импульсов противоположного знака и результат точного интегрирования, соответственно, а на рисунке 11 – сигнал на выходе преобразователя (![]() ). По осям координат отложены безразмерные величины (масштабы одинаковы). Видно, что сигнал близок по форме к «идеальной» кривой (рисунок 10), однако наблюдается характерный отрицательный «хвост» разрядного типа. Уровень этого отрицательного выброса может быть использован как критерий качества интегрирования, если на него наложить соответствующее ограничение. Кроме того, уровень этого сигнала почти в 5 раз меньше по сравнению с уровнем «идеального» сигнала. Из выражения (10) видно, что чувствительность датчика уменьшается по мере возрастания коэффициента демпфирования.
). По осям координат отложены безразмерные величины (масштабы одинаковы). Видно, что сигнал близок по форме к «идеальной» кривой (рисунок 10), однако наблюдается характерный отрицательный «хвост» разрядного типа. Уровень этого отрицательного выброса может быть использован как критерий качества интегрирования, если на него наложить соответствующее ограничение. Кроме того, уровень этого сигнала почти в 5 раз меньше по сравнению с уровнем «идеального» сигнала. Из выражения (10) видно, что чувствительность датчика уменьшается по мере возрастания коэффициента демпфирования.
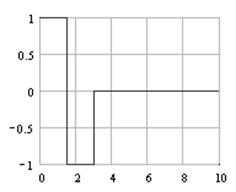


Рисунок 9 –Закон воздействия |
| Рисунок 10 – Идеальное интегрирование |
| Рисунок 11 – Сигнал на выходе «реального» интегратора |
При отсутствии члена ![]() в левой части (9) получается система первого порядка (апериодическое звено)
в левой части (9) получается система первого порядка (апериодическое звено)
 ,
,
в которой ![]() выполняет роль своеобразной постоянной времени. Уравнением данного типа, например, описывается схема замещения генераторного магнитоупругого преобразователя с одной обмоткой, обладающего четко выраженными интегрирующими свойствами [10], что подтверждает реальность решения поставленной задачи..
выполняет роль своеобразной постоянной времени. Уравнением данного типа, например, описывается схема замещения генераторного магнитоупругого преобразователя с одной обмоткой, обладающего четко выраженными интегрирующими свойствами [10], что подтверждает реальность решения поставленной задачи..
Заключение
Основные результаты работы сводятся к следующему.
1) Сделано предположение, что влияние скорости и перемещения боеприпаса на процесс взаимодействия с преградой может быть учтено раздельно, путем введения соответствующих функциональных множителей в выражение для силовой характеристики преграды.
2) Показано, что параметры начального участка процесса взаимодействия боеприпаса с преградой, являющегося основным с точки зрения функционирования КДЦ, могут быть выявлены на основе использования эмпирических формул для полного пути внедрения боеприпаса и экспериментально установленных фактов.
3) Предложены два способа аппроксимации начального участка силовой характеристики преграды, а именно: в виде кусочно-линейной зависимости силы сопротивления и зависимости текущей площади сечения головной части боеприпаса от его перемещения. Приведенный пример расчета КДЦ кассетного боевого элемента иллюстрирует применение предложенной методики.
4) Проанализирована возможность использования КДЦ интеграторного типа, позволяющего оценивать скорость боеприпаса после выхода в запреградное пространство и отфильтровывать колебательные наложения.
Данные результаты получены при приближенной, т.е. одномерной постановке задачи, когда траектория боеприпаса в преграде считается прямолинейной. Тем не менее, предложенная методика дает возможность достаточно адекватно оценивать работоспособность контактных датчиков цели, поскольку их срабатывание происходит в пределах начального участка (переднего фронта) закона силы сопротивления преграды, и, следовательно, с практической точки зрения влиянием искривления траектории снаряда при последующем внедрении в преграду можно пренебречь. Предложенный подход может быть использован и в случае более прочных преград, но в пределах ограниченного диапазона углов, отсчитываемых от нормали.
Список литературы
1. Сагомонян А.Я. Проникание (проникание твердых тел в сжимаемые сплошные среды). М.: Изд-во МГУ, 1974. 300 с.
2. Ионов В.Н. Прочность боеприпаса при взаимодействии с преградой. М.: Машиностроение, 1979. 423 с.
3. Велданов В.А., Наумов А.Н. Расчет характеристик пространственного проникания тел в сопротивляющиеся среды. М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. 24 с.
4. Сулин Г.А. Теоретические основы расчета сенсорных систем: учеб. пособие. СПб. : БГТУ («Военмех»), 2000. 64 с.
5. Средства поражения и боеприпасы: учебник / А.В. Бабкин, В.А. Велданов, Е.Ф. Грязнов и др.; под ред. В.В. Селиванова. М.: Изд-во МГТУ им. Н.Э. Баумана, 2008. 984 с.
6. Андреев С.Г., Овчинников А.Ф., Охитин В.Н. Основы конструкции и действия боеприпасов. Ч. 1. Теория и расчет. М.: ЦНИИНТЭИ и ТЭИ, 1989. 155 с.
7. Третьяков Г.М. Боеприпасы артиллерии. М.: Воениздат, 1947. 536 с.
8. Прохоров Б.А. Боеприпасы артиллерии. М.: Машиностроение, 1973. 512 с.
9. Куров В.Д., Должанский Ю.М. Основы проектирования пороховых ракетных снарядов. М.: Оборонгиз, 1961. 294 с.
10. Ефремов А.К. Автономные информационные и управляющие системы. В 4 т. Т. 4. М.: ООО НИЦ «Инженер», ООО «Онико-М», 2011. 330 с.
11. Инженерные методы исследования ударных процессов / Г.С. Батуев, Ю.В. Голубков, А.К. Ефремов, А.А. Федосов. 2-е изд. М.: Машиностроение, 1977. 240 с.
12. Проектирование датчиков для измерения механических величин / Под ред. Е.П. Осадчего. М.: Машиностроение, 1979. 480 с.
13. Пеллинец В.С. Измерение ударных ускорений. М.: Изд-во стандартов, 1975. 288 с.
14. Крылов А.Н. О некоторых дифференциальных уравнениях математической физики, имеющих приложение в технических вопросах. 5-еизд. М.-Л.: ГИТТЛ, 1950. 369 с.
Публикации с ключевыми словами: аппроксимация, контактный датчик цели, начальный этап внедрения снаряда, силовая характеристика преграды, эмпирические формулы, датчик цели интеграторного типа
Публикации со словами: аппроксимация, контактный датчик цели, начальный этап внедрения снаряда, силовая характеристика преграды, эмпирические формулы, датчик цели интеграторного типа
Смотри также:
- Аппроксимация функции предпочтений лица, принимающего решения, в задаче многокритериальной оптимизации. Методы на основе планов второго порядка
- Итерационный метод решения СЛАУ на основе механической аналогии
- Исследование применения полиномиальной аппроксимации для преобразования данных в системе сжатия телеметрической информации
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||
 .
.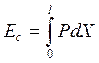 ,
,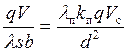
 – коэффициент свойств преграды;
– коэффициент свойств преграды;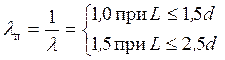
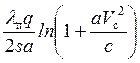


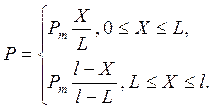
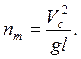
 ,
,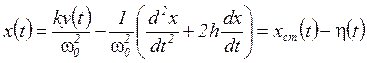 ,
, ,
,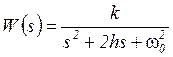 ,
, ,
,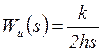 ;
;  ;
; 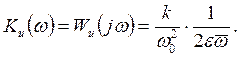
 ,
,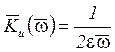 .
.



