научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 10, октябрь 2013
DOI: 10.7463/1013.0605836
Россия, МГТУ им. Н.Э. Баумана
ООО МТЦ «САУРУС-ЭНЕРГО»
Биогеографию определяют как науку на стыке биологии и географии, которая изучает закономерности географического распространения и распределения животных, растений и микроорганизмов. Математическая теория биогеографии начала развиваться в 60-е годы прошлого века с фундаментальной работы Роберта МакАртура (RobertMacArthur) и Эдварда Вилсона (EdwardWilson) «Теория островной биогеографии» [1]. Здесь под островом (island) понимается среда обитания, географически изолированная от других сред. Качество острова с точки зрения его пригодности для обитания видов определяет индекс пригодности (Habitat Suitability Index, HSI). Значения этого индекса полагают зависящими от набора параметров острова (SuitabilityIndexVariables, SIVs), примерами которых являются температура, влажность, разнообразие растительности и т.д.
Острова, обладающие более высоким индексом пригодности, имеют большое число населяющих их видов. Для таких островов характерно, во-первых, большое число индивидов, которые эмигрируют на соседние острова. Во-вторых, в силу насыщенности этих островов видами, они имеют низкий уровень иммиграции. Напротив, системы с малыми значениями HSI имеют, как правило, небольшое число видов. Для этих островов характерным является низкий уровень эмиграции и высокий уровень иммиграции.
Важно, что процесс иммиграции на «бедные» острова может повысить пригодность этих островов (поскольку пригодность острова пропорциональна разнообразию ее форм жизни). Если пригодность острова остается низкой, то проживающие на этом острове виды приобретают тенденцию к исчезновению, которая, однако, далее открывает путь к дополнительной иммиграции с «богатых» островов. Таким образом, острова с низкой пригодностью оказываются более динамичными с точки зрения числа населяющих их видов, чем острова, имеющие высокую пригодность.
Модели биогеографии могут быть использованы и используются для решения задач оптимизации на основе следующей аналогии. Полагаем, что значение целевой функции есть индекс пригодности соответствующего острова-решения. Хорошее решение отождествляем с островом, имеющим высокий индекс пригодности, а плохое – наоборот, с островом с низким значением этого индекса. Хорошие решения подвержены изменениям в гораздо меньшей степени, чем плохие. К тому же хорошие решения могут использовать плохие решения для повышения своего качества. Аналогично, плохие решения могут повышать свое качество с использованием хороших решений.
Указанный подход к решению задачи оптимизации с использованием модели биогеографии называют BBO (Biogeography-BasedOptimization). BBOотносится к классу методов, вдохновленных природой, к которым принадлежат также такие широко известные методы, как генетический, роя частиц (PSO) [2], муравьиной колонии (ACO) [3], пчел (BCO) [4] и большое число других методов [5].
Работа преследует три цели. Во-первых, поскольку нам незнакомы публикации на русском языке по методу BBO, представить русскоязычному читателю этот новый метод глобальной оптимизации. Во-вторых, показать эффективность метода на одной из классических тестовых задач глобальной непрерывной многомерной оптимизации. В-третьих, исследовать эффективность метода при решении актуальной практической задачи об оптимальном размещении устройств регулирования напряжения в электроэнергетической сети.
В первом разделе представляем элементы теории биогеографии, используемые в дальнейшем изложении. Во втором разделе приводим постановку задачи глобальной непрерывной оптимизации и даем схему метода BBO. Третий раздел посвящен исследованию эффективности метода на одной из трудных тестовых задач глобальной оптимизации. В четвертом разделе рассматриваем решение задачи об оптимальном размещении устройств регулирования напряжения в электрической сети. В Заключении формулируем основные результаты работы и перспективы ее развития.
1. Элементы теории биогеографии
Элементы теории биогеографии представляем, следуя публикации [6]. Простейшую модель распространения видов на одном из островов иллюстрирует рисунок 1, показывающий уровни иммиграции ![]() и эмиграции
и эмиграции ![]() в функции числа видов
в функции числа видов ![]() данного острова.
данного острова.
Рисунок 1 показывает, что максимум иммиграции ![]() имеет место при минимальном числе видов на острове. С увеличением числа видов остров становится все более переполненным, и все меньшее число видов‑иммигрантов способно пережить иммиграцию. Число видов острова, при котором иммиграция становится равной нулю, обозначаем
имеет место при минимальном числе видов на острове. С увеличением числа видов остров становится все более переполненным, и все меньшее число видов‑иммигрантов способно пережить иммиграцию. Число видов острова, при котором иммиграция становится равной нулю, обозначаем ![]() .
.
Для эмиграции имеет место противоположная тенденция. При нулевом числе видов острова эмиграция равна, очевидно, нулю. С увеличением числа видов вследствие переполненности острова большее число видов получает стимулы для того, чтобы покинуть этот остров и исследовать другие острова. Эмиграция достигает максимального значения, равного ![]() , при числе видов, равном
, при числе видов, равном ![]() .
.
Равенство уровней иммиграции и эмиграции достигается при некотором числе видов ![]() . Данное число является метастабильным, поскольку возможны случайные всплески, как иммиграции, так и эмиграции, обусловленные, например, эпидемиями, изменениями климата острова и прочее.
. Данное число является метастабильным, поскольку возможны случайные всплески, как иммиграции, так и эмиграции, обусловленные, например, эпидемиями, изменениями климата острова и прочее.
В действительности зависимости уровней иммиграции и эмиграции от числа видов, конечно, не являются линейными. Однако канонический метод BBOиспользует рассмотренные линейные модели.

Рисунок 1 – Простейшая модель распространения видов на острове:
![]() ‑ интенсивность иммиграции;
‑ интенсивность иммиграции; ![]() ‑ интенсивность эмиграции;
‑ интенсивность эмиграции; ![]() ‑ число видов на острове
‑ число видов на острове
Обозначим ![]() вероятность того, что рассматриваемый остров содержит
вероятность того, что рассматриваемый остров содержит ![]() видов. Изменение вероятности
видов. Изменение вероятности ![]() за период времени
за период времени ![]() определяет выражение
определяет выражение
![]()
![]()
![]() ). (1)
). (1)
Справедливость выражения вытекает из того факта, что для получения ![]() видов в момент времени
видов в момент времени ![]() должно выполняться одно из следующих условий:
должно выполняться одно из следующих условий:
1) в момент времени ![]() остров содержал
остров содержал ![]() видов, и за период времени
видов, и за период времени ![]() иммиграция и эмиграция отсутствовали (первое слагаемое в формуле (1));
иммиграция и эмиграция отсутствовали (первое слагаемое в формуле (1));
2) в момент времени ![]() остров содержал
остров содержал ![]() видов, и за указанный период имела место иммиграция (второе слагаемое в (1));
видов, и за указанный период имела место иммиграция (второе слагаемое в (1));
3) в момент времени ![]() остров содержал
остров содержал ![]() видов, и за тот же период наблюдалась эмиграция (третье слагаемое в (1)).
видов, и за тот же период наблюдалась эмиграция (третье слагаемое в (1)).
В пределе при ![]() из выражения (1) следует система
из выражения (1) следует система ![]() -го обыкновенных дифференциальных уравнений (ОДУ)
-го обыкновенных дифференциальных уравнений (ОДУ)
 (2)
(2)
В векторной форме эта система приобретает классический для теории биогеографии вид
![]() ,
, ![]() , (3)
, (3)
где ![]() ;
; ![]() -матрицу
-матрицу ![]() определяет формула
определяет формула
 ; (4)
; (4)
![]() ‑ вектор начальных условий;
‑ вектор начальных условий; ![]() - символ транспонирования.
- символ транспонирования.
Для линейной модели распространения видов, представленной на рисунке 1, уровни иммиграции и эмиграции определяют, соответственно, выражения
 ,
, 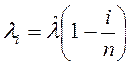 ;
; ![]() . (5)
. (5)
Ограничимся случаем, когда максимальные уровни эмиграции и иммиграции равны, то есть когда ![]() . В этом случае, очевидно, для любого
. В этом случае, очевидно, для любого ![]() имеет место равенство
имеет место равенство
![]() (6)
(6)
и матрица ![]() приобретает вид
приобретает вид
 . (7)
. (7)
Известно [6], что установившееся решение системы ОДУ (2) при ее любых допустимых начальных условиях определяет формула
 , (8)
, (8)
где ![]() ‑ собственный вектор матрицы
‑ собственный вектор матрицы ![]() , соответствующий ее нулевому собственному значению;
, соответствующий ее нулевому собственному значению;
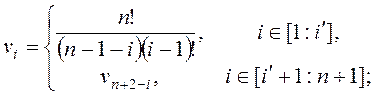
 . (9)
. (9)
Здесь ![]() ‑ символ ближайшего целого большего.
‑ символ ближайшего целого большего.
В работе [6] показано, что в соответствие с уравнением (2) в установившемся состоянии острова, как с низким, так и с высоким числом видов имеют относительно низкую вероятность изменения этого числа. Напротив, острова, имеющие среднее число видов, подвержены изменениям своей численности видов с высокой вероятностью.
Из выражения (8) вытекает, что сумма элементов вектора ![]() равна единице и распределение значений компонентов этого вектора симметрично относительно среднего элемента (элемента с номером
равна единице и распределение значений компонентов этого вектора симметрично относительно среднего элемента (элемента с номером ![]() ). Например, для случая
). Например, для случая ![]() компоненты вектора
компоненты вектора ![]() имеют приближенные значения
имеют приближенные значения
![]() .
.
2. Простановка задачи и схема метода биогеографии
Рассматриваем задачу целочисленной глобальной условной оптимизации
![]() , (10)
, (10)
где ![]() – целевая функция,
– целевая функция, ![]() –
– ![]() -мерный вектор целочисленных варьируемых параметров,
-мерный вектор целочисленных варьируемых параметров, ![]() – искомый оптимальный вектор варьируемых параметров,
– искомый оптимальный вектор варьируемых параметров, ![]() – искомое оптимальное значение целевой функции,
– искомое оптимальное значение целевой функции, ![]() ‑ параллелепипед допустимых значений вектора варьируемых параметров:
‑ параллелепипед допустимых значений вектора варьируемых параметров:
![]() . (11)
. (11)
Введем следующие обозначения [6].
![]() ‑ остров.
‑ остров.
![]() ‑ вектор параметров, определяющих остров
‑ вектор параметров, определяющих остров ![]() ;
; ![]() .
.
![]() ‑ допустимое значение
‑ допустимое значение ![]() -ой компоненты вектора
-ой компоненты вектора ![]() ;
; ![]() .
.
![]() ‑ индекс пригодности (фитнесс) острова
‑ индекс пригодности (фитнесс) острова ![]() ;
; ![]() .
.
![]() ‑ совокупность
‑ совокупность ![]() островов, экосистема.
островов, экосистема.
![]() ‑ интенсивность иммиграции, монотонная невозрастающая функция величины
‑ интенсивность иммиграции, монотонная невозрастающая функция величины ![]() . Вероятность того, что SIVsсоседних островов будут мигрировать на данный остров
. Вероятность того, что SIVsсоседних островов будут мигрировать на данный остров ![]() , пропорциональна интенсивности иммиграции
, пропорциональна интенсивности иммиграции ![]() этого острова.
этого острова.
![]() ‑ интенсивность эмиграции, монотонная неубывающая функция величины
‑ интенсивность эмиграции, монотонная неубывающая функция величины ![]() . Вероятность того, что SIVsданного острова будут мигрировать на соседние острова, пропорциональна интенсивности эмиграции
. Вероятность того, что SIVsданного острова будут мигрировать на соседние острова, пропорциональна интенсивности эмиграции ![]() этого острова.
этого острова.
![]() ‑ вероятностный оператор модификации острова
‑ вероятностный оператор модификации острова ![]() , изменяющий остров
, изменяющий остров ![]() на основе экосистемы
на основе экосистемы ![]() . Вероятность того, что остров будет модифицирован, пропорциональна интенсивности его иммиграции
. Вероятность того, что остров будет модифицирован, пропорциональна интенсивности его иммиграции ![]() . Вероятность того, что источником модификации станет остров
. Вероятность того, что источником модификации станет остров ![]() , пропорциональна его интенсивности эмиграции
, пропорциональна его интенсивности эмиграции ![]() . Псевдокод оператора
. Псевдокод оператора ![]() представлен на рисунке 2.
представлен на рисунке 2.

Рисунок 2 – Псевдокод оператора ![]() модификации острова
модификации острова
Заметим, что приведенное определение оператора ![]() гарантирует, что допустимый вектор
гарантирует, что допустимый вектор ![]() , соответствующий выбранному острову, после его модификации останется допустимым.
, соответствующий выбранному острову, после его модификации останется допустимым.
![]() ‑ свободный параметр элитизма оператора
‑ свободный параметр элитизма оператора ![]() , равный числу лучших островов экосистемы
, равный числу лучших островов экосистемы ![]() , для которого величина
, для которого величина ![]() устанавливается равной нулю;
устанавливается равной нулю; ![]() .
.
![]() ‑ вероятностный оператор мутации, случайным образом изменяющий SIVs острова
‑ вероятностный оператор мутации, случайным образом изменяющий SIVs острова ![]() , основываясь на вероятности
, основываясь на вероятности ![]() , полученной в результате решения системы ОДУ вида (2), (6). Псевдокод оператора для острова
, полученной в результате решения системы ОДУ вида (2), (6). Псевдокод оператора для острова ![]() представлен на рисунке 3.
представлен на рисунке 3.

Рисунок 3 – Псевдокод оператора ![]() мутации острова
мутации острова
Из приведенного определения оператора мутации следует, что он не нарушает ограничений на SIVs.
![]() ‑ свободный параметр элитизма оператора
‑ свободный параметр элитизма оператора ![]() , имеющий смысл числа лучших островов экосистемы
, имеющий смысл числа лучших островов экосистемы ![]() , для которых вероятность мутации устанавливается равной нулю;
, для которых вероятность мутации устанавливается равной нулю; ![]() .
.
![]() ‑ функция перехода экосистемы, изменяющая эту систему в процессе одной итерации процесса оптимизации по правилу
‑ функция перехода экосистемы, изменяющая эту систему в процессе одной итерации процесса оптимизации по правилу
![]() ,
,
где ![]() ‑ совокупности уровней иммиграции и эмиграции всех островов экосистемы соответственно;
‑ совокупности уровней иммиграции и эмиграции всех островов экосистемы соответственно; ![]() ‑ наборы значений
‑ наборы значений ![]() всех островов до и после мутации соответственно. Другими словами, выполнение функции перехода
всех островов до и после мутации соответственно. Другими словами, выполнение функции перехода ![]() начинается с вычисления уровней иммиграции и эмиграции каждого из островов. Затем производится модификация каждого из островов и перевычисление значений их индексов пригодности. Наконец, выполняются мутации всех островов и повторное перевычисление их пригодностей.
начинается с вычисления уровней иммиграции и эмиграции каждого из островов. Затем производится модификация каждого из островов и перевычисление значений их индексов пригодности. Наконец, выполняются мутации всех островов и повторное перевычисление их пригодностей.
Во введенных обозначениях алгоритм биогеографии определяет триплет ![]() . Здесь
. Здесь ![]() ‑ операция, которая инициализирует экосистему и вычисляет для каждого из островов начальное значение его индекса пригодности;
‑ операция, которая инициализирует экосистему и вычисляет для каждого из островов начальное значение его индекса пригодности; ![]() - условие завершения итераций. Исходя из общих для всех популяционных алгоритмов принципов, операция
- условие завершения итераций. Исходя из общих для всех популяционных алгоритмов принципов, операция ![]() может быть реализована с помощью того или иного генератора случайных чисел, на основе некоторого эвристического решения рассматриваемой задачи оптимизации, с помощью какой-либо задачезависимой процедуры. По тем же правилам условие
может быть реализована с помощью того или иного генератора случайных чисел, на основе некоторого эвристического решения рассматриваемой задачи оптимизации, с помощью какой-либо задачезависимой процедуры. По тем же правилам условие ![]() может зависеть от числа итераций, индекса пригодности лучшего острова, некоторой другой задачезависимой величины.
может зависеть от числа итераций, индекса пригодности лучшего острова, некоторой другой задачезависимой величины.
Полагаем размер ![]() экосистемы постоянным, хотя, подобно некоторым вариантам генетических алгоритмов, возможно использование экосистем переменного размера. Кроме того полагаем, хотя это также не является обязательным, что функции
экосистемы постоянным, хотя, подобно некоторым вариантам генетических алгоритмов, возможно использование экосистем переменного размера. Кроме того полагаем, хотя это также не является обязательным, что функции ![]() ,
, ![]() линейны и имеют одинаковые максимальные значения, равные
линейны и имеют одинаковые максимальные значения, равные ![]() . Значения параметров элитизма операторов модификации и мутации принимаем одинаковыми и равными
. Значения параметров элитизма операторов модификации и мутации принимаем одинаковыми и равными ![]() .
.
Общая схема метода BBO имеет следующий вид.
1) Представляем задачу оптимизации в терминах остров и их SIVsи HSI. Инициализируем максимальное число островов ![]() , максимальные интенсивности иммиграции и эмиграции
, максимальные интенсивности иммиграции и эмиграции ![]() , максимальный уровень мутации
, максимальный уровень мутации ![]() (см. ниже) и параметр элитизма
(см. ниже) и параметр элитизма ![]() .
.
2) С помощью оператора ![]() инициализируем случайный набор островов ‑ потенциальных решений задачи оптимизации.
инициализируем случайный набор островов ‑ потенциальных решений задачи оптимизации.
3) В соответствие с функцией перехода экосистемы ![]() для каждого из островов вычисляем интенсивности иммиграции и эмиграции.
для каждого из островов вычисляем интенсивности иммиграции и эмиграции.
4) С помощью оператора модификации ![]() , используя вычисленные интенсивности иммиграции и эмиграции, модифицируем каждый из неэлитных островов. Перевычисляем индексы пригодности этих островов.
, используя вычисленные интенсивности иммиграции и эмиграции, модифицируем каждый из неэлитных островов. Перевычисляем индексы пригодности этих островов.
5) Обновляем для каждого из островов вероятность соответствующего числа видов и с этой вероятностью применяем к каждому из неэлитных островов оператор мутации ![]() . Перевычисляем индексы пригодности обновленных островов.
. Перевычисляем индексы пригодности обновленных островов.
6) Проверяем выполнение условия окончания итераций ![]() . Если это условие не выполнено, то переходим к шагу 3, если выполнено, то завершаем вычисления.
. Если это условие не выполнено, то переходим к шагу 3, если выполнено, то завершаем вычисления.
После шагов 2, 4, 5 проверяем допустимость полученных решений. Недопустимые решения соответствующим образом изменяем.
Поясним схемы операторов модификации ![]() и мутации
и мутации ![]()
Оператор модификации ![]() . Каждый из островов
. Каждый из островов ![]() может быть модифицирован с некоторой вероятностью
может быть модифицирован с некоторой вероятностью ![]() . Если по этому принципу для модификации отобран остров
. Если по этому принципу для модификации отобран остров ![]() , то, используя значение его уровня иммиграции
, то, используя значение его уровня иммиграции ![]() , для каждой компоненты вектора
, для каждой компоненты вектора ![]() вероятностно принимаем решение о том, должна ли быть изменена эта компонента или нет. Если данная компонента должна быть изменена, то, используя соответствующие значения уровней эмиграции
вероятностно принимаем решение о том, должна ли быть изменена эта компонента или нет. Если данная компонента должна быть изменена, то, используя соответствующие значения уровней эмиграции ![]() других решений, вероятностно определяем компонента какого из этих решений
других решений, вероятностно определяем компонента какого из этих решений ![]() должна мигрировать, чтобы заменить указанную компоненту в решении
должна мигрировать, чтобы заменить указанную компоненту в решении ![]() .
.
Заметим, что, например, в отличие от генетического алгоритма и алгоритма эволюционных стратегий, в методе BBO миграция не создает новых решений, но лишь адаптивно модифицирует их [7].
Оператор мутации![]() . Как отмечалось выше, равновесие видов на острове может быть нарушено по многим причинам. Это означает, что индекс пригодности острова HSI подвержен случайным возмущениям. Оператор мутации моделирует данное явление с помощью случайных мутаций SIV. Полагаем, что уровень мутации решения
. Как отмечалось выше, равновесие видов на острове может быть нарушено по многим причинам. Это означает, что индекс пригодности острова HSI подвержен случайным возмущениям. Оператор мутации моделирует данное явление с помощью случайных мутаций SIV. Полагаем, что уровень мутации решения ![]() обратно пропорционален вероятности
обратно пропорционален вероятности ![]() и определяется формулой
и определяется формулой
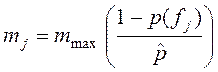 , (10)
, (10)
где ![]() ‑ свободный параметр алгоритма,
‑ свободный параметр алгоритма, ![]() . Вероятности
. Вероятности ![]() вычисляются путем интегрирования системы ОДУ (2). Данная схема мутации имеет целью увеличение разнообразия островов. Схема делает малопригодные решения более подверженными мутации, которая дает им шанс быть улучшенными. Эта схема также не исключает возможность изменения высокопригодных решений. Таким образом, данная схема реализует принцип элитизма, обеспечивая с высокой вероятностью сохранение лучших решений.
вычисляются путем интегрирования системы ОДУ (2). Данная схема мутации имеет целью увеличение разнообразия островов. Схема делает малопригодные решения более подверженными мутации, которая дает им шанс быть улучшенными. Эта схема также не исключает возможность изменения высокопригодных решений. Таким образом, данная схема реализует принцип элитизма, обеспечивая с высокой вероятностью сохранение лучших решений.
3. Исследование эффективности метода биогеографии
Метод биогеографии реализован нами в программной системе Matlab [8]. Метод реализован для непрерывной задачи глобальной безусловной оптимизации. Исследование эффективности метода выполнено на известной тестовой функции Растригина
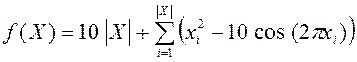 ,
,
![]() ,
,
которая имеет один глобальный минимум, в котором значение функции равно нулю.
Если не оговорено противное, исследование выполнено при следующих значениях свободных параметров метода:
‑ размер экосистемы ![]() ;
;
‑ вероятность модификации острова ![]() ;
;
‑ коэффициент мутации ![]() ;
;
‑ параметр элитизма ![]() .
.
В качестве условия окончания итераций используем стагнацию вычислений в течение ![]() итераций. Число запусков Matlabпрограммы, реализующей метод BBO, полагаем равным 20 или 30 (см. ниже).
итераций. Число запусков Matlabпрограммы, реализующей метод BBO, полагаем равным 20 или 30 (см. ниже).
Используем следующие критерии, определяющие эффективность метода:
· ![]() ‑ оценка вероятности локализации глобального минимума с заданной точностью
‑ оценка вероятности локализации глобального минимума с заданной точностью ![]() ;
;
· ![]() ‑ среднее достигнутое значение функции
‑ среднее достигнутое значение функции ![]() ;
;
· ![]() ‑ среднеквадратическое отклонение достигнутого значения функции
‑ среднеквадратическое отклонение достигнутого значения функции ![]() ;
;
· ![]() ‑ среднее число итераций;
‑ среднее число итераций;
· ![]() ‑ среднее число вычислений значений функции
‑ среднее число вычислений значений функции ![]() (среднее число испытаний).
(среднее число испытаний).
Некоторые результаты исследования представлены в таблицах 1, 2.
Таблица 4.1. Эффективность алгоритма: ![]() ;
; ![]() ;
; ![]()
Критерий эффективности алгоритма | |||||
|
|
|
|
|
|
0,005 | 0,63 | 0,54 | 0,62 | 75 | 2243 |
0,01 | 0,67 | 0,44 | 0,68 | 44 | 1322 |
0,03 | 0,60 | 0,54 | 0,73 | 43 | 1283 |
0,07 | 0,70 | 0,37 | 0,65 | 49 | 1470 |
0,1 | 0,7 | 0,37 | 0,65 | 50 | 1477 |
0,4 | 0,43 | 0,67 | 0,66 | 54 | 1601 |
Таблица 4.2. Эффективность алгоритма: ![]() ;
; ![]() ;
; ![]()
Критерий эффективности алгоритма | |||||
|
|
|
|
|
|
0,005 | 0,50 | 1,43 | 1,17 | 128 | 3819 |
0,01 | 0,50 | 1,57 | 1,24 | 128 | 3839 |
0,03 | 0,26 | 1,34 | 1,17 | 140 | 4184 |
0,07 | 0,33 | 0,94 | 0,86 | 155 | 4648 |
0,1 | 0,26 | 1,01 | 0,78 | 144 | 4307 |
0,4 | 0,26 | 1,58 | 1,22 | 155 | 4653 |
Результаты таблицы 4.1 иллюстрируют рисунки 4 – 8, а таблицы 4.2 ‑ рисунки 9 – 12.

Рисунок 4 − Оценка вероятности локализации глобального минимума ![]() в функции величины коэффициента мутации
в функции величины коэффициента мутации ![]() :
: ![]() ;
; ![]() ;
; ![]()
Из рисунка 4 видно, что с увеличением значения коэффициента мутации ![]() оценка вероятности локализации глобального минимума
оценка вероятности локализации глобального минимума ![]() уменьшается. Оптимальные значения величины
уменьшается. Оптимальные значения величины ![]() лежат в интервале [0,07; 0,1]. Отметим, что эти результаты получены при малом размере экосистемы
лежат в интервале [0,07; 0,1]. Отметим, что эти результаты получены при малом размере экосистемы ![]() .
.
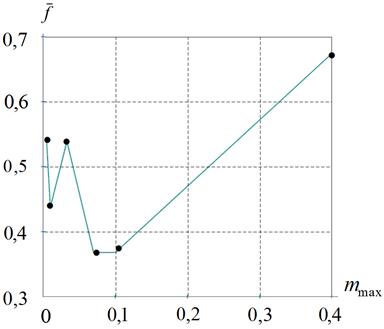
Рисунок 5 − Среднее достигнутое значение фитнесс ![]() в функции величины коэффициента мутации
в функции величины коэффициента мутации ![]() :
: ![]() ;
; ![]() ;
; ![]()
Рисунок 5 показывает наличие четкого минимума в зависимости ![]() . При значениях коэффициента мутации
. При значениях коэффициента мутации ![]() , больших 0,1, быстро возрастает среднее достигнутое значение целевой функции
, больших 0,1, быстро возрастает среднее достигнутое значение целевой функции ![]() . С точки зрения минимизации этой величины оптимальные значения величины
. С точки зрения минимизации этой величины оптимальные значения величины ![]() также лежат в интервале [0,07; 0,1].
также лежат в интервале [0,07; 0,1].

Рисунок 6 − Среднеквадратическое отклонение ![]() в функции величины коэффициента мутации
в функции величины коэффициента мутации ![]() :
: ![]() ;
; ![]() ;
; ![]()
Из рисунка 6 вытекает, что по критерию минимума среднеквадратического отклонения ![]() оптимальными являются малые значения величины
оптимальными являются малые значения величины ![]() , равные примерно 0,05. На правом краю найденного выше диапазона
, равные примерно 0,05. На правом краю найденного выше диапазона ![]() (0,03; 0,07) среднеквадратическое отклонение оказывается приемлемым.
(0,03; 0,07) среднеквадратическое отклонение оказывается приемлемым.

Рисунок 7 − Среднее число итераций ![]() в функции величины коэффициента мутации
в функции величины коэффициента мутации ![]() :
: ![]() ;
; ![]() ;
; ![]()
Рисунок 7 иллюстрирует тот факт, что зависимость среднего числа итераций ![]() от коэффициента мутации имеет минимум в окрестности
от коэффициента мутации имеет минимум в окрестности ![]() . При значениях этого параметра, меньших 0,1, величина
. При значениях этого параметра, меньших 0,1, величина ![]() быстро возрастает.
быстро возрастает.

Рисунок 8 − Среднее число испытаний ![]() в функции величины коэффициента мутации
в функции величины коэффициента мутации ![]() :
: ![]() ;
; ![]() ;
; ![]()
Характер зависимости среднего числа испытаний ![]() от величины коэффициента мутации
от величины коэффициента мутации ![]() (рисунок 8), ожидаемо, подобен зависимости
(рисунок 8), ожидаемо, подобен зависимости ![]() . Как и последняя функция, функция
. Как и последняя функция, функция ![]() имеет минимум в окрестности
имеет минимум в окрестности ![]() .
.
Рисунки 9 – 12 соответствуют высокой размерности вектора варьируемых параметров функции Растригина (![]() ). Поэтому рассмотренные выше зависимости в данном случае имеют несколько иной вид. Прежде всего, обращает на себя внимание низкая оценка вероятности локализации глобального минимума
). Поэтому рассмотренные выше зависимости в данном случае имеют несколько иной вид. Прежде всего, обращает на себя внимание низкая оценка вероятности локализации глобального минимума ![]() (рисунок 9). Объясняется этот факт малым размером используемой экосистемы (величина
(рисунок 9). Объясняется этот факт малым размером используемой экосистемы (величина ![]() равна всего 10). Отметим также значительно больший диапазон изменения величин
равна всего 10). Отметим также значительно больший диапазон изменения величин ![]() ,
, ![]() ,
, ![]() ,
, ![]() (зависимость
(зависимость ![]() не представлена в силу отмеченной выше близости ее к зависимости
не представлена в силу отмеченной выше близости ее к зависимости ![]() ).
).
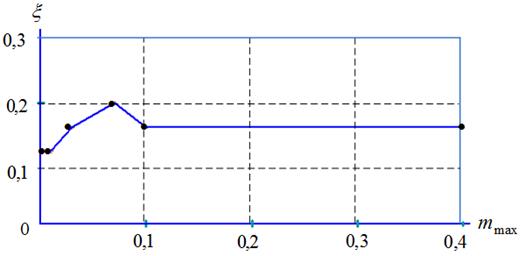
Рисунок 9 − Вероятности локализации глобального минимума ![]() в функции величины коэффициента мутации
в функции величины коэффициента мутации ![]() :
: ![]() ;
; ![]() ;
; ![]()

Рисунок 10 − Среднее достигнутое значение фитнесс ![]() в функции величины коэффициента мутации
в функции величины коэффициента мутации ![]() :
: ![]() ;
; ![]() ;
; ![]()

Рисунок 11 − Среднеквадратичное отклонение ![]() в функции величины коэффициента мутации
в функции величины коэффициента мутации ![]() :
: ![]() ;
; ![]() ;
; ![]()
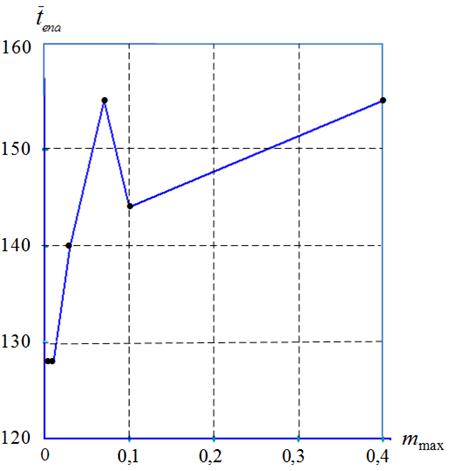
Рисунок 12 − Средне число итераций ![]() в функции величины коэффициента мутации
в функции величины коэффициента мутации ![]() :
: ![]() ;
; ![]() ;
; ![]()
Из рисунков 9 – 12 следует, что при высокой размерности вектора варьируемых параметров ![]() целесообразно использовать значения коэффициента мутации
целесообразно использовать значения коэффициента мутации ![]() из интервала
из интервала ![]() .
.
Результаты сравнения эффективности метода BBOс эффективностью значительного числа эволюционных и популяционных методов на широком классе тестовых задач глобальной оптимизации представлены в работе [6].
4. Оптимизация размещения компенсаторов реактивной мощности в электросетях
Вследствие интенсификации и усложнения технологических процессов на современных производствах, в настоящее время все большую долю в общем объеме суммарных электрических нагрузок занимают нагрузки с повышенным потреблением реактивной мощности. Такие нагрузки оказывают отрицательное влияние на качество электроэнергии питающих сетей. С другой стороны, нормальная работа электрооборудования зависит от качества электроэнергии этих сетей. Взаимовлияние электрооборудования и питающей электрической сети называют их электромагнитной совместимостью.
Основным средством обеспечения электромагнитной совместимости электрооборудования и питающей сети является компенсация реактивной мощности в этой сети. Проблема компенсации реактивной мощности включает в себя задачи выбора целесообразных компенсирующих источников реактивной мощности (компенсаторов), определение требуемой мощности этих источников, а также их размещение в системе электроснабжения. Решение проблемы компенсации реактивной мощности позволяет существенно снизить потери мощности в сетях [9].
В последние годы опубликовано значительное число работ, посвященных исследованию эффективности решения задачи об оптимальном размещении компенсаторов [10]. Использование метода BBOдля решения этой задачи предложено в 2009 году [11] (см. также работы [12, 13]).
5.1. Постановка задачи. Активную и реактивную мощности электрического потока из ![]() -ой электрической шины в такую же j-ю шину определяют уравнения
-ой электрической шины в такую же j-ю шину определяют уравнения


соответственно. Здесь ![]() ‑ напряжения на указанных шинах,
‑ напряжения на указанных шинах, ![]() ‑ угол сдвига напряжений между шинами,
‑ угол сдвига напряжений между шинами, ![]() − реактивное сопротивление линии передачи между ними.
− реактивное сопротивление линии передачи между ними.
Изменение реактивной мощности на ![]() -шине имеет вид
-шине имеет вид
![]() ,
,
где ![]() – реактивная мощность установленного компенсатора.
– реактивная мощность установленного компенсатора.
Рассматриваем компенсаторы двух типов ‑ конденсаторная батарея и шунтирующий реактор (индуктивность). Полагаем заданными величины ![]() , определяющие диапазоны допустимых реактивных мощностей компенсаторов указанных типов, так что справедливы неравенства
, определяющие диапазоны допустимых реактивных мощностей компенсаторов указанных типов, так что справедливы неравенства
![]() ;
; ![]() .
.
Введем в рассмотрение ![]() -мерный вектор решений
-мерный вектор решений ![]() такой, что
такой, что ![]() ‑ мощность компенсатора, установленного на
‑ мощность компенсатора, установленного на ![]() -ой шине. Здесь знаки плюс и минус определяют емкость и индуктивность соответствующего компенсатора. Подчеркнем, что приведенное определение вектора
-ой шине. Здесь знаки плюс и минус определяют емкость и индуктивность соответствующего компенсатора. Подчеркнем, что приведенное определение вектора ![]() обеспечивает выполнение следующего ограничения: разрешена установка только одного компенсатора на каждую из шин. Также имеет место следующее ограничение: общее число компенсаторов в сети
обеспечивает выполнение следующего ограничения: разрешена установка только одного компенсатора на каждую из шин. Также имеет место следующее ограничение: общее число компенсаторов в сети ![]() не должно превышать величины
не должно превышать величины ![]() или, другими словами, общее число ненулевых элементов вектора
или, другими словами, общее число ненулевых элементов вектора ![]() не должно превышать этой величины.
не должно превышать этой величины.
Ставится задача найти типы, мощности и места расположения компенсаторов, которые обеспечивают минимум суммарных потерь мощности электрической сети ![]() :
:
![]() . (11)
. (11)
Здесь ![]() ‑ множество допустимых значений вектора варьируемых параметров
‑ множество допустимых значений вектора варьируемых параметров ![]() , формируемое указанными выше ограничениями.
, формируемое указанными выше ограничениями.
Поскольку допустимы только целочисленные значения компонентов ![]() вектора
вектора ![]() , задачу (11) следует классифицировать как задачу целочисленного программирования. Наша MatLab-реализация BBOметода ориентирована на решение непрерывной задачи глобальной оптимизации. Поэтому используем известный прием решения задач целочисленного программирования, заключающийся в решении задачи (11) как непрерывной и последующем округлении значений компонентов полученного вектора решения до целых [14].
, задачу (11) следует классифицировать как задачу целочисленного программирования. Наша MatLab-реализация BBOметода ориентирована на решение непрерывной задачи глобальной оптимизации. Поэтому используем известный прием решения задач целочисленного программирования, заключающийся в решении задачи (11) как непрерывной и последующем округлении значений компонентов полученного вектора решения до целых [14].
При заданных значениях компонентов вектора ![]() суммарные потери мощности в электрической сети
суммарные потери мощности в электрической сети ![]() могут быть вычислены с помощью большого числа отечественных и зарубежных программ ‑ RastrWin, КОСМОС, MUSTANG, DAKAR, АНАРЭС-2000, EnergyCS, PSS/E, DigSilent, EUROSTAGи другие. Используем программный продукт PowerFactory компании DlgSilent, преимуществами которого являются точность и достоверность результатов, объектная ориентированность, широкая функциональность, наличие русской версии и ее локальной поддержки [15].
могут быть вычислены с помощью большого числа отечественных и зарубежных программ ‑ RastrWin, КОСМОС, MUSTANG, DAKAR, АНАРЭС-2000, EnergyCS, PSS/E, DigSilent, EUROSTAGи другие. Используем программный продукт PowerFactory компании DlgSilent, преимуществами которого являются точность и достоверность результатов, объектная ориентированность, широкая функциональность, наличие русской версии и ее локальной поддержки [15].
Общую структуру используемого программного обеспечения иллюстрирует рисунок 13.

Рисунок 13 – Структура программного обеспечения
5.2. Оптимизация электросети IEEE 9[16]
Схема электросети IEEE 9 в интерфейсе системы PowerFactory представлена на рисунках 14, 15.
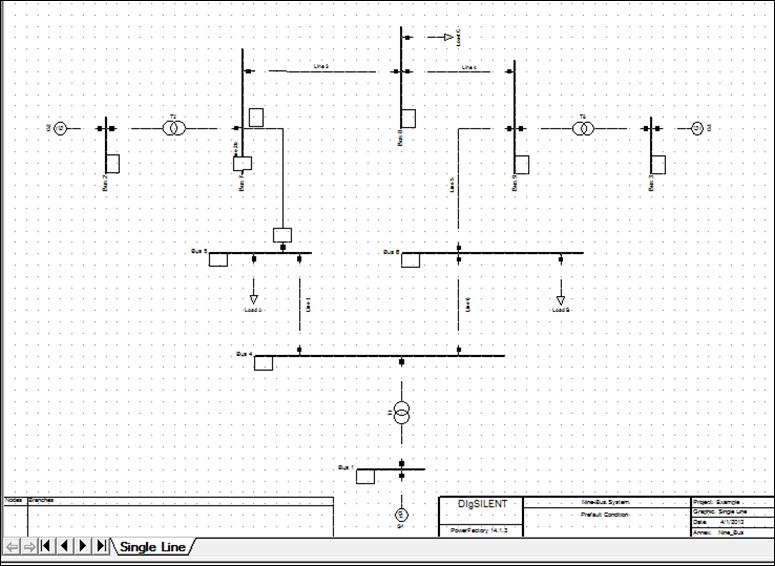
Рисунок 14 − Схема девятишинной электрической сетиIEEE 9: интерфейс системы PowerFactory

![]()
а) б) в) г) д)
Рисунок 15 – Условные обозначения: а) генератор; б) шина; в) линия электропередач; г) нагрузка; д) трансформатор
На реактивную мощность компенсаторов и их число накладываем ограничения, определяемые следующими равенствами:
![]()
![]() МВар;
МВар; ![]() ;
;
![]() МВар;
МВар; ![]() .
.
Поскольку число шин в рассматриваемой системе равно девяти, размерность вектора варьируемых параметров ![]() также равна этой величине.
также равна этой величине.
Задача решена при следующих значениях свободных параметров алгоритма:
![]() .
.
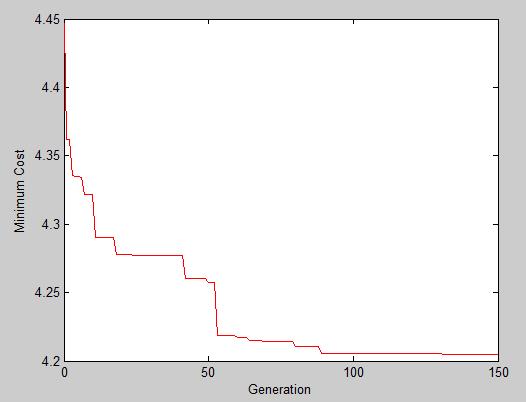
Сходимость алгоритма иллюстрирует рисунок 16; результаты решения задачи представлены в таблице 3.
Рисунок 16 − Сходимость алгоритма биогеографии при оптимизации тестовой электрической сети IEEE 9: интерфейс системы PowerFactory
Таблица 3. Результаты решения задачи оптимизации электрической сети IEEE 9
Потери активной мощности в сети IEEE 9 без использования компенсаторов составляют 4,63 МВт. Представленному в таблице 3 решению соответствуют потери мощности, равные 4,2 MВт. Таким образом, за счет оптимизации набора и размещения компенсаторов удалось снизить потери активной мощности в рассматриваемой сети примерно на 9,2%.
5.3. Оптимизация электрической сети Кубани
Электрическая сеть Кубани включает в себя 45 генераторов, 614 шин; 483 линии электропередач, 100 трансформаторов. Рассматриваем задачу расстановки компенсаторов в 110 киловольтной части этой сети, в которой числа шин, линий передач и трансформаторов равны 488, 419, 20 соответственно. Моделирование этой сети в системе PowerFactory показывает, что без использования компенсаторов потери активной мощности в сети составляют 148,8 МВт.
Оптимизация данной сети выполнена при ограничениях, определяемых равенствами
![]()
![]() МВар;
МВар; ![]() ;
;
![]() МВар;
МВар; ![]() .
.
Размерность вектора варьируемых параметров ![]() равна числу шин. Задача решена при указанных выше значениях свободных параметров алгоритма.
равна числу шин. Задача решена при указанных выше значениях свободных параметров алгоритма.
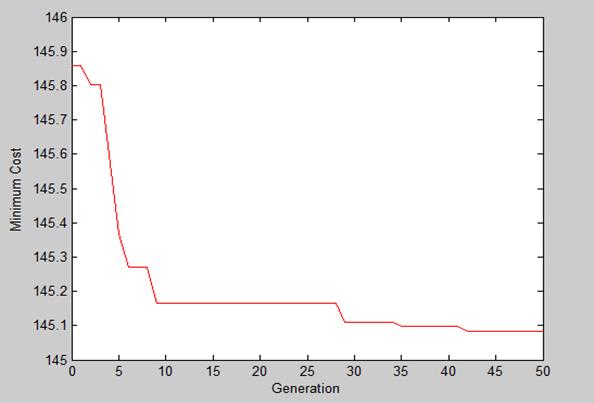
Сходимость алгоритма иллюстрирует рисунок 17, аналогичный рисунку 16.
Рисунок 17 −Сходимость алгоритма биогеографии при оптимизации электрической сети Кубани: интерфейс системы PowerFactory
Результат решения задачи представлены в таблице 4.
Таблица 4. Результаты решения задачи оптимизации электрической сети Кубани
Решению задачи, которое представлено в таблице 4 соответствуют потери активной мощности, равные 145,07 MВт. Таким образом, применение указанных в таблице 4 пяти компенсаторов и их оптимальное размещение позволяют снизить потери мощности на 2,5%.
В работе представлен перспективный метод глобальной оптимизации – метод биогеографии. Эффективность метода и разработанного программного обеспечения продемонстрирована на примере известной сложной задачи минимизации многомерной функции Растригина.
Выполнена интеграция разработанного в системе MatLab программного обеспечения, реализующего BBOметод, с известным программным продуктом PowerFactory компании DlgSilent, который предназначен для решения широкого круга задач электроэнергетики и используется нами для расчета суммарных потерь мощности в исследуемой электрической сети. С помощью программного комплекса MatLabBBO+ PowerFactory проведено исследование эффективности метода биогеографии при решении задач оптимизации электрической сети IEEE 9 и сети Кубани. За счет оптимизации набора и размещения компенсаторов удалось снизить потери активной мощности в указанных сетях примерно на 9,2% и 2,5% соответственно.
Как и в работе [6] метод биогеографии показал свою высокую эффективность. В развитие работы авторы предполагают исследовать природу этого факта. Предполагается также синтез и исследование эффективности гибридных популяционных методов, построенных на основе метода биогеографии.
Работа поддержана грантом РФФИ 12-07-00222а «Управление знаниями, извлекаемыми из текстовых документов, на основе кластеризации онтологий».
Список литературы
1. MacArthur R.H., Wilson E.O. The Theory of Island Biogeography. Princeton University Press, 1967. 224 p.
2. Карпенко А.П., Селиверстов Е.Ю. Глобальная оптимизация методом роя частиц. Обзор // Информационныетехнологии. 2010. № 2. С. 25-34.
3. Dréo J., Siarry P. Continuous interacting ant colony algorithm based on dense heterarchy // Future Generation Computer Systems. 2004. No. 20. P. 841-856.
4. Karaboga D., Basturk B. Artificial Bee Colony (ABC) optimization algorithm for solving constrained optimization problems // In: Foundations of Fuzzy Logic and Soft Computing. Springer Verlag, 2007. P. 789-797. (Ser. Lecture Notes in Computer Science; vol. 4529). DOI: 10.1007/978-3-540-72950-1_77
5. Карпенко А.П. Популяционные алгоритмы глобальной поисковой оптимизации. Обзор новых и малоизвестных алгоритмов // Приложение к журналу «Информационные технологии». 2012. № 7. С. 1-32.
6. Simon D. Biogeography-Based Optimization // IEEE Transactions on Evolutionare Computation. December 2008. Vol. 12, no. 6. P. 702-713. DOI: 10.1109/TEVC.2008.919004
7. Holland J.H. Adaptation in Natural and Artificial Systems. Cambridge: MIT Press, 1992. 228 p.
8. Потемкин В.Г. Введение в MATLAB. М.: Диалог-МИФИ, 2000. 256 с.
9. FACTS (Flexible Alternative Current Transmission Systems) - гибкиесистемыпередачипеременноготокакакфизическаяосноваумныхсетей. Режим доступа: http://energyfuture.ru/facts-flexible-alternative-current-transmission-systems (дата обращения 23.08.2013).
10. Subramanian A., Ravi G. Multi-type FACTS placement for loss minimization using biogeography based optimization // Archives of Electrical Engineering. 2012. Vol. 61, no. 4. P. 517-531.
11. Rarick R., Simon D., Villaseca F.E., Vakaranam B. Biogeography-based optimization and the solution of the power flow problem // Proceedings of the IEEE International Conference on Systems, Man and Cybernetics (San Antonio TX, USA, October 2009). SMC 2009. P. 1003-1008. DOI: 10.1109/ICSMC.2009.5346046
12. Bhattachary A., Chattopadhyay P.K. Solution of optimal reactive power flow using Biogeographybased optimization // International Journal of Energy and Power Engineering. 2010. Vol. 3, no. 4. P. 269-277.
13. Bhattacharya A., Chattopadhyay P.K. Biogeography - base optimization for different economic load dispatch problems // IEEE Transactions on Power Systems. 2010. Vol. 25, iss. 2. P. 1064-1077. DOI: 10.1109/TPWRS.2009.2034525
14. Groenwold A.A., Stander N., Snyman J.A. A pseudo-discrete rounding method for structural optimization // Structural Optimization. 1996. No. 11. P. 218-227.
15. DIgSILENT. PowerFactory. Available at: http://www.digsilent.de/index.php/products-powerfactory.html , accessed 23.08.2013.
16. Nallagalva S.K., Kumar Kirar M.K., Agnihotri G. Transient Stability Analysis of the IEEE 9 Bus Electric Power System // International Journal of Scientific Engineering and Technology. 2012. Vol. 1, no. 3. P. 161-166.
Публикации с ключевыми словами: задача глобальной оптимизации, метод биогеографии, задача оптимизации электрической сети
Публикации со словами: задача глобальной оптимизации, метод биогеографии, задача оптимизации электрической сети
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||