научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 11, ноябрь 2013
DOI: 10.7463/1113.0604082
УДК 519.6
Россия, МГТУ им. Н.Э. Баумана
Введение
В состав многих современных изделий и сооружений области высоких технологий, таких как летательные аппараты, реакторные установки АЭС и др., входят гидромеханические системы различного назначения. Разработка и последующая эксплуатация таких систем связаны с поиском решения двух типов экстремальных задач – оптимизации и диагностики. Задачи первого типа возникают, например, при выборе оптимальных параметров систем или реализации оптимального управления. Обеспечение безопасной и эффективной эксплуатации требует решения задач второго типа: коррекции математических моделей и диагностирования систем по результатам косвенных измерений. Входными данными для диагностирования являются результаты экспериментального определения следственных характеристик системы или процесса, включая регистрируемые параметры колебательных и ударных процессов. Искомыми являются причинные характеристики, к которым относятся коэффициенты уравнений расчетной динамической модели, граничные условия, геометрические и ряд других характеристик. В задачах этого типа следует учитывать недифференцируемость и многоэкстремальность критериальных функций ввиду наличия кратных частот, а также неполноты и зашумленности информации, полученной при измерениях. Значительная трудоемкость численного решения обратных спектральных задач обусловлена их некорректностью, которая чаще всего проявляется в неустойчивости решения относительно погрешностей входных данных.
Оптимизационное исследование сложных объектов основано на разработке и последующем уточнении их математических моделей [1–4]. Усложнение модели объекта, в свою очередь, вызывает необходимость создания новых, более эффективных методов оптимизации. Следует отметить, что в аспекте динамики спектры колебаний содержат существенную информацию об исследуемом объекте. Возникают задачи определения оптимальных собственных характеристик системы или процесса, а также использования собственных характеристик для коррекции моделей и диагностирования систем. Одним из активно развивающихся направлений, связанных с проблемой безопасности реакторных установок АЭС, является исследование двухфазных газожидкостных потоков. Некоторые результаты как численного моделирования, так и экспериментальных исследований двухфазных потоков представлены в работах [5–8]. Актуальной является задача идентификации аномалий фазового состава теплоносителя в контуре реакторной установки. Используемый далее общий подход основан на разработке и применении математических моделей систем, математических методов расчета основных динамических характеристик систем, методов теории обратных задач, методов глобальной оптимизации.
В первом разделе формулируется задача глобальной оптимизации. Краткое описание гибридных алгоритмов оптимизации дано во втором разделе; там же приведены сведения о реализации алгоритмов в виде прикладных программ. Численный пример применения гибридных алгоритмов рассматривается в третьем разделе, где представлены результаты решения модельной задачи диагностирования фазового состава теплоносителя в циркуляционном контуре реакторной установки.
1. Постановка задач
Некоторые стандартные постановки экстремальных задач для гидромеханических систем приведены в работе [9]. Так, задача коррекции расчетной динамической модели и диагностирования системы как обратная спектральная задача связана с поиском вектора переменных управления, при котором первые ![]() собственных частот модели совпадают с составляющими некоторого заданного ограниченного спектра или близки к ним. Для оценки уровня рассогласования сравниваемых характеристик объекта используется векторный способ описания. Так как информация о формах колебаний объекта зачастую отсутствует или является существенно неполной, ниже рассматривается только рассогласование между частотными составляющими нормального и заданного спектров. Возможные подходы основаны на минимизации квадратичной функции рассогласования или минимизации максимальной из функций рассогласования спектральных составляющих. Так, для попарно сравниваемых спектральных составляющих может быть построено следующее конечное множество критериев рассогласования
собственных частот модели совпадают с составляющими некоторого заданного ограниченного спектра или близки к ним. Для оценки уровня рассогласования сравниваемых характеристик объекта используется векторный способ описания. Так как информация о формах колебаний объекта зачастую отсутствует или является существенно неполной, ниже рассматривается только рассогласование между частотными составляющими нормального и заданного спектров. Возможные подходы основаны на минимизации квадратичной функции рассогласования или минимизации максимальной из функций рассогласования спектральных составляющих. Так, для попарно сравниваемых спектральных составляющих может быть построено следующее конечное множество критериев рассогласования
![]() ,
,
где ![]() собственные значения, относящиеся к исходному (текущему) и заданному спектрам. Требуется найти такой вектор переменных управления, который приводит к наименьшим отличиям между сравниваемыми спектрами, т.е. следует произвести настройку модели объекта на заданный спектр. Это эквивалентно одновременной минимизации всех
собственные значения, относящиеся к исходному (текущему) и заданному спектрам. Требуется найти такой вектор переменных управления, который приводит к наименьшим отличиям между сравниваемыми спектрами, т.е. следует произвести настройку модели объекта на заданный спектр. Это эквивалентно одновременной минимизации всех ![]() критериев рассогласования: требуется найти
критериев рассогласования: требуется найти
![]() ;
;
здесь векторная целевая функция записывается в виде
![]() .
.
Задача коррекции расчетной динамической модели системы формулируется в следующем виде: определить вектор переменных управления ![]() , который минимизирует максимальное значение критерия рассогласования, т.е. ищется
, который минимизирует максимальное значение критерия рассогласования, т.е. ищется
![]() .
. ![]()
Решением сформулированной дискретной минимаксной задачи ![]() является такой вектор
является такой вектор ![]() , принадлежащий множеству допустимых значений, при котором скалярная критериальная функция
, принадлежащий множеству допустимых значений, при котором скалярная критериальная функция ![]()
![]() принимает минимальное значение. В случае, когда
принимает минимальное значение. В случае, когда ![]() , спектр частот настраиваемой модели полностью совпадает с заданным спектром по
, спектр частот настраиваемой модели полностью совпадает с заданным спектром по ![]() низшим частотам. Последнее условие вследствие неполноты экспериментальных данных и погрешностей, полученных при измерениях, не выполняется. В последующем рассматривается регуляризованная задача
низшим частотам. Последнее условие вследствие неполноты экспериментальных данных и погрешностей, полученных при измерениях, не выполняется. В последующем рассматривается регуляризованная задача ![]() с многоэкстремальной не всюду дифференцируемой критериальной функцией
с многоэкстремальной не всюду дифференцируемой критериальной функцией ![]() , где
, где ![]() параметр регуляризации [9, 10]. Используется предположение о том, что отношения приращений функций к приращениям аргументов не превышают некоторого порога. Последний определяется ограниченной энергией изменений в системе и может быть описан с помощью константы Липшица.
параметр регуляризации [9, 10]. Используется предположение о том, что отношения приращений функций к приращениям аргументов не превышают некоторого порога. Последний определяется ограниченной энергией изменений в системе и может быть описан с помощью константы Липшица.
В обобщение постановок экстремальных задач выбора оптимальных параметров, коррекции расчетной динамической модели и диагностирования системы, принимается следующая формулировка задачи глобальной оптимизации: требуется найти
 , (1)
, (1)
где
![]() , (2)
, (2)
![]() ; (3)
; (3)
использованы обозначения: ![]() целевая функция;
целевая функция; ![]() вектор переменных управления;
вектор переменных управления; ![]() функции ограничений задачи,
функции ограничений задачи, ![]() ;
; ![]() конечное множество индексов;
конечное множество индексов; ![]() допустимая область;
допустимая область; ![]() область поиска;
область поиска; ![]() глобальное решение;
глобальное решение; ![]() размерность задачи;
размерность задачи; ![]() ; через
; через ![]() обозначено
обозначено ![]() -мерное вещественное линейное пространство. Функции
-мерное вещественное линейное пространство. Функции ![]() ,
, ![]() ,
, ![]() , задачи (1) – (3) предполагаются непрерывными липшицевыми. Предполагается также, что действительная функция
, задачи (1) – (3) предполагаются непрерывными липшицевыми. Предполагается также, что действительная функция ![]() является многоэкстремальной, не всюду дифференцируемой и для нее задана вычислительная процедура, позволяющая определять значения функции в точках допустимой области. Необходимо также учесть возможную высокую трудоемкость вычисления критериальных функций, что может потребовать значительных вычислительных ресурсов.
является многоэкстремальной, не всюду дифференцируемой и для нее задана вычислительная процедура, позволяющая определять значения функции в точках допустимой области. Необходимо также учесть возможную высокую трудоемкость вычисления критериальных функций, что может потребовать значительных вычислительных ресурсов.
2. Гибридные алгоритмы глобальной оптимизации
2.1 Алгоритм M-PCALMS
Детерминированные методы решения задач глобальной оптимизации многоэкстремальных функций к настоящему времени достаточно хорошо разработаны и находят широкое применение. Однако их эффективность существенно ограничена размерностью задачи. В случае большого числа переменных применяют алгоритмы стохастической глобальной оптимизации. К ним относятся алгоритмы моделируемого отжига, генетические, управляемого случайного поиска и др. [11–13]. Вместе с тем, чувствительность к выбору параметров алгоритмов этого типа, устанавливаемых пользователем или определяемых содержанием задачи, сильно влияет на скорость сходимости итерационного процесса. В настоящее время значительное внимание уделяется проблеме гибридизации алгоритмов глобальной оптимизации [14, 15]. Гибридный алгоритм, как правило, объединяет какой-либо стохастический алгоритм сканирования пространства переменных, используемый при определении области, перспективной на глобальный экстремум, и детерминированный метод локального поиска. При этом вычислительная эффективность результирующего алгоритма по сравнению с исходными алгоритмами может значительно возрасти [16, 17].
Одним из наиболее мощных современных стохастических алгоритмов глобальной оптимизации является алгоритм PCA [18]. Существенным шагом алгоритма является сравнительная оценка качества решения, определяемого текущей и предшествующей конфигурацией системы. Пробное приближение принимается с определенной вероятностью, что исключает сходимость к локальному минимуму при поиске глобального решения. Позднее в работе [19] был предложен более мощный алгоритм M-PCA [19]. Работа алгоритмов PCA и M-PCA основана на использовании аналогии с физическими процессами абсорбции и рассеяния частиц при ядерных реакциях. В алгоритме PCA для исследования области поиска используется одна частица. На начальном шаге выбирается пробное решение (Old_Config), которое затем модифицируется посредством стохастического возмущения (Perturbation()), что позволяет найти новое решение (New_Config). С помощью функции Fitness() дается сравнительная оценка нового и предыдущего решений, на основании которой новое решение может быть принято или отвергнуто. Если новое решение отвергнуто, то происходит переход к функции Scattering(), реализующей схему Метрополиса. Для сканирования области, перспективной на минимум, применяются функции Perturbation() и Small_Perturbation(). Новое решение принимается, если оно лучше предыдущего (абсорбция); если найденное решение хуже предыдущего, то происходит переход в отдаленную область пространства поиска (рассеяние), что позволяет преодолевать локальные минимумы. Эффективность описанного поиска глобального решения алгоритмом PCA может быть значительно повышена за счет одновременного использования большого числа частиц. Такой подход реализует алгоритм M-PCA, который непосредственно ориентирован на применение в среде параллельных вычислений. Наилучшее решение определяется с учетом данных о всех частицах, участвующих в процессе. Единственным задаваемым параметром для алгоритма M-PCA является число итераций.
Локальный поиск в гибридном алгоритме должен быть реализован с учетом предположения о недифференцируемости критериальной функции. Поэтому при выборе детерминированного метода локального поиска необходимо учитывать его способность работать с такими функциями. К числу современных методов, специально разработанных для решения задач недифференцируемой оптимизации, относятся, например, bundle-метод с ограниченной памятью [20], субградиентный метод [21] и др. Альтернативный подход основан на построении сглаживающих аппроксимаций критериальных функций и последующем применении мощных классических алгоритмов оптимизации гладких функций [22]. В работе [23] представлен двухпараметрический метод построения сглаживающих аппроксимаций не всюду дифференцируемых функций и предложен вариант метода линеаризации LMS со сглаживанием. Разработан гибридный алгоритм, объединяющий стохастический алгоритм M-PCAсканирования пространства переменных и детерминированный метод LMSлокального поиска. Результирующий алгоритм M-PCALMS реализован в виде прикладного программного обеспечения [24].
2.2 Алгоритм M-PCAMNM
Решение подзадачи локального поиска для не всюду дифференцируемой критериальной функции можно также получить с помощью методов, не использующих производные. В работе [25] представлен вариант симплекс-метода Нелдера-Мида, сходимость которого доказана теоретически. Кроме того, алгоритм, реализующий модифицированный метод Нелдера-Мида, является робастным для задач с разрывными или зашумленными критериальными функциями. Отмечена более высокая вычислительная эффективность модифицированной версии метода по сравнению с классической. Таким образом, может быть предложен гибридный алгоритм глобальной недифференцируемой оптимизации M-PCAMNM, объединяющий стохастический алгоритм M-PCA (общий поиск в пространстве переменных) и модифицированный симплекс-метод Нелдера–Мида (локальный поиск). Ниже представлен фрагмент псевдокода нового гибридного алгоритма M-PCANMN.
0 GenerateaninitialsolutionOld_Config
Best_Fitness = Fitness (Old_Config)
Update Blackboard
For ![]() to # of particles
to # of particles
For ![]() to # of iterations
to # of iterations
Update Blackboard
Perturbation ( )
If Fitness (New_Config) > Fitness (Old_Config)
If Fitness (New_Config) > Best_Fitness
Best_Fitness := Fitness (New_Config)
End If
Old_Config := New_Config
Exploration ( )
Else
Scattering ( )
End If
End For
End For
2. Exploration ( )
For ![]() to # of iterations
to # of iterations
Small_Perturbation ( )
Local search
using Modified Nelder-Mead Simplex Method
Check stopping criterion:
Find global solution Best Fitness
Else continue
If Fitness (New_Config) > Best_Fitness
Best_Fitness := Fitness (New_Config)
End If
Old_Config := New_Config
End For
Return
3. Scattering ( )
![]() ( Fitness (New_Config)) / (Best_Fitness)
( Fitness (New_Config)) / (Best_Fitness)
If ![]() > random(0, 1)
> random(0, 1)
Old_Config := random solution
Else
Exploration ( )
End If
Return
В состав алгоритма M-PCAMNM входят также стандартные процедуры Perturbation( ) и Small_Perturbation( ) [19]. Другой гибридный алгоритм M-PCASFC, объединяющий стохастический алгоритм M-PCA и детерминированный метод кривой, заполняющей пространство, используемый при локальном поиске, представлен в работе [26].
3. Численные примеры
Рассматривается модельная задача диагностирования фазового состава теплоносителя в главном циркуляционном контуре серийного блока ВВЭР-1000 [6]. Переменными управления являются относительные значения скорости звука ![]() в теплоносителе на участках, соответствующих: зоне нагрева теплоносителя в напорном баке системы компенсации объема СКО
в теплоносителе на участках, соответствующих: зоне нагрева теплоносителя в напорном баке системы компенсации объема СКО ![]() ; выходному объему реактора
; выходному объему реактора ![]() ; активной зоне реактора
; активной зоне реактора ![]() ; проточной части главного циркуляционного насоса циркуляционной петли с СКО
; проточной части главного циркуляционного насоса циркуляционной петли с СКО ![]() . При отсутствии в теплоносителе второй фазы нормальный спектр
. При отсутствии в теплоносителе второй фазы нормальный спектр ![]() определяется максимальными значениями скорости звука на выделенных участках.
определяется максимальными значениями скорости звука на выделенных участках.
В первом примере аномальный спектр ![]() получен при наличии двухфазной смеси как в выходном объеме, так и в активной зоне реактора, при этом:
получен при наличии двухфазной смеси как в выходном объеме, так и в активной зоне реактора, при этом: ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Таблица 1 – Нормальный и аномальный спектры частот колебаний теплоносителя
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0.89 | 6.77 | 9.82 | 15.44 | 15.96 | 18.94 | 24.57 | 26.69 | 27.07 | 30.52 |
| 0.86 | 6.77 | 9.36 | 15.33 | 15.96 | 18.86 | 21.22 | 26.67 | 26.93 | 29.41 |
После определения области, содержащей глобальный минимум, завершающие итерации алгоритма M-PCALMSпроводятся с использованием градиентной информации для сглаживающих аппроксимаций критериальной функции. Сходимость решения иллюстрируют рисунки 1, 2 (Niter – число итераций).
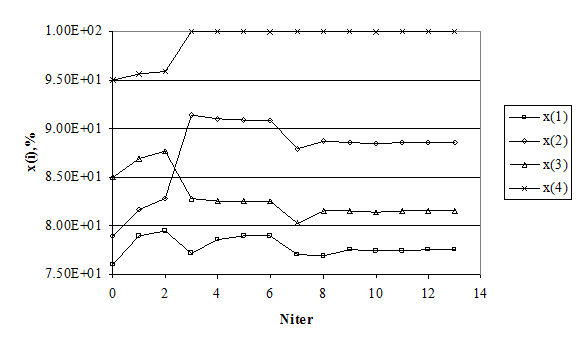
Рис. 1. Изменение значений переменных управления ![]() на завершающих итерациях алгоритма
на завершающих итерациях алгоритма
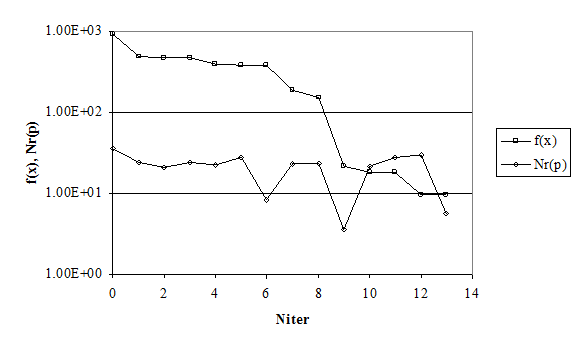
Рис. 2. Уточнение значений критериальной функции ![]() и нормы
и нормы ![]() вектора направления поиска на завершающих итерациях алгоритма
вектора направления поиска на завершающих итерациях алгоритма
Получено приближенное решение задачи: ![]() ;
; ![]() ;
; ![]() ;
; ![]() . При этом относительная погрешность определения значений переменных управления не превышает
. При этом относительная погрешность определения значений переменных управления не превышает ![]() , а точность настройки спектра частот имеет порядк
, а точность настройки спектра частот имеет порядк ![]() Гц.
Гц.
Во втором примере аномальный спектр ![]() получен при наличии двухфазной смеси как в выходном объеме, так и в активной зоне реактора, при этом:
получен при наличии двухфазной смеси как в выходном объеме, так и в активной зоне реактора, при этом: ![]() ;
; ![]() ;
; ![]() ;
; ![]() . После определения области, содержащей глобальный минимум, завершающие итерации алгоритма M-PCAMNM проводятся с использованием модифицированного симплекс-метода Нелдера-Мида.
. После определения области, содержащей глобальный минимум, завершающие итерации алгоритма M-PCAMNM проводятся с использованием модифицированного симплекс-метода Нелдера-Мида.
Таблица 2 – Нормальный и аномальный спектры частот колебаний теплоносителя
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0.89 | 6.77 | 9.82 | 15.44 | 15.96 | 18.94 | 24.57 | 26.69 | 27.07 | 30.52 |
| 0.86 | 6.77 | 9.36 | 15.33 | 15.96 | 18.86 | 21.22 | 26.67 | 26.93 | 29.41 |
Сходимость решения иллюстрируют рисунки 3, 4 (Niter – число итераций). Получено приближенное решение задачи: ![]() ;
; ![]() ;
; ![]() ;
; ![]() . При этом относительная погрешность определения значений переменных управления не превышает
. При этом относительная погрешность определения значений переменных управления не превышает ![]() , а точность настройки спектра частот имеет порядк
, а точность настройки спектра частот имеет порядк ![]() Гц.
Гц.

Рис. 3. Изменение значений переменных управления ![]() на завершающих итерациях алгоритма
на завершающих итерациях алгоритма

Рис. 4. Уточнение значений критериальной функции ![]() на завершающих итерациях алгоритма
на завершающих итерациях алгоритма
Выводы. Представлены два гибридных алгоритма глобальной оптимизации, объединяющие современный стохастический алгоритм M-PCA, используемый при сканировании пространства переменных, и методы локального поиска. В первом алгоритме M-PCALMSлокальный поиск проводится методом линеаризации со сглаживающимися аппроксимациями критериальной функции. Во втором алгоритме M-PCAMNM при при локальном поиске используется модифицированный симплекс-метод Нелдера-Мида. Разработано программное обеспечение, реализующее гибридные алгоритмы. Предложен подход к решению задачи вычислительной диагностики фазового состава теплоносителя в контуре реакторной установки с использованием гибридных алгоритмов. Модельные расчеты показали возможность идентификации аномалий фазового состава теплоносителя на выделенных участках контура с достаточной для приложений точностью.
Работа выполнена при финансовой поддержке Министерства образования и науки РФ (грант Президента РФ по поддержке научных исследований ведущих научных школ РФ, код НШ-4748.2012.8).
Список литературы
1. Ватульян А.О. Обратные задачи в механике деформируемого твердого тела. М.: Физматлит, 2007. 224 с.
2. Horváth M. Inverse spectral problems and closed exponential systems // Annals of Mathematics. 2005. Vol. 162, no. 2. P. 885-918.
3. Pulecchi T., Casella F., Lovera M. Object-oriented modelling for spacecraft dynamics: Tools and applications // Simulation Modelling and Theory. 2010. V. 18, no. 1. P. 63-86.
4. Lopez I., Sarigul-Klijn N. A review of uncertainty in flight vehicle structural damage monitoring, diagnosis and control: Challenges and opportunities // Progress in Aerospace Sciences. 2010. V. 46, no. 7. P. 247-273.
5. Böttcher M., Krüβmann R. Primary loop study of a VVER-1000 reactor with special focus on coolant mixing // Nuclear Engineering and Design. 2010. V. 240, no. 9. P. 2244-2253.
6. De Oliveira M.V., de Almeida J.C.S. Applications of artificial intelligence techniques in modeling and control of a nuclear power plant pressurizer system // Progress in Nuclear Energy. 2013. V. 63. P. 71-85.
7. Poullikkas A. Effects of two-phase liquid-gas flow on the performance of nuclear reactor cooling pumps // Progress in Nuclear Energy. 2003. V. 42, no. 1. P. 3-10.
8. Kinelev V.G., Shkapov P.M., Sulimov V.D. Application of global optimization to VVER-1000 reactor diagnostics // Progress in Nuclear Energy. 2003. V. 43, no. 1-4. P. 51-56.
9. Pang S., Chen L., Zhang M., Yin Y., Chen T., Zhou J., Liao D. Numerical simulation two phase flows of casting filling process using SOLA particle level set method // Applied Mathematical Modelling. 2010. V. 34, no. 12. P. 4106-4122.
10. Yang X., Schlegel J.P., Liu Y., Paranjape S., Hibiki T., Ishii M. Experimental study of interfacial area transport in air-water two-phase flow in a scaled ![]() BWR rod bundle // International Journal of Multiphase Flow. 2013. V. 50. P. 16-32.
BWR rod bundle // International Journal of Multiphase Flow. 2013. V. 50. P. 16-32.
11. Сулимов В.Д., Шкапов П.М. Методология решения экстремальных задач для механических и гидромеханических систем // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2012. Спец. вып. № 8. С. 17-34.
12. Li X.Y., Law S.S. Adaptive Tikhonov regularization for damage detection based on nonlinear model updating // Mechanical Systems and Signal Processing. 2010. V. 24, no. 2. P. 1646-1664.
13. Egea J.A., Vazquez E., Banga J.R., Martí R. Improoved scatter search for the global optimization of computationally expensive dynamic models // Journal of Global Optimization. 2009. V. 43, no. 2. P. 175-190.
14. Bertsimas D., Nohadami O. Robust optimization with simulated annealing // Journal of Global Optimization. 2010. V. 48, no. 3. P. 323-334.
15. Lu T.-C., Juang J.-C. Quantum-inspired space search algorithm (QSSA) for global numerical optimization // Applied Mathematics and Computation. 2011. V. 218, no. 6. P. 2516-2532.
16 La Cruz D., Noguera G. Hybrid spectral gradient method for the unconstrained minimization problem // Journal of Global Optimization. 2009. V. 44, no. 2. P. 193-212.
17. Thangaraj R., Pant M., Abraham A., Bouvry P. Particle swarm optimization: hybridization perspectives and experimental illustrations // Applied Mathematics and Computation. 2011. Vol. 217, no. 12. P. 5208-5226.
18. Gaviano M., Lera D., Steri A.M. A local search method for continuous global optimization // Journal of Global Optimization. 2010. V. 48, no. 1. P. 73-85.
19. Voglis C., Parsopoulos K.E., Papageorgiou D.G., Lagaris I.E., Vrahatis M.N. MEMSODE: A global optimization software based on hybridization of population-based algorithms and local searches // Computer Physics Communications. 2012. V. 183, no. 2. P. 1139-1154.
20. Sacco W.F., de Oliveira C.R.E. A new stochastic optimization algorithm based on particle collisions // Transactions of the American Nuclear Society. Proceedings of the 2005 ANS Annual Meeting. 2005. V. 92. P. 657-659.
21. Luz E.F.P., Becceneri J.C., de Campos Velho H.F. A new multi-particle collision algorithm for optimization in a high performance environment // Journal of Computational Interdisciplinary Sciences. 2008. V. 1. P. 3-10.
22. Karmitsa N., Mäkelä M.M. Limited memory bundle method for large bound constrained optimization: convergence analysis // Optimization Methods & Software. 2010. V. 25, no. 6. P. 895-916.
23. Bagirov A.M., Jin L., Karmitsa N., Al Nuaimat A., Sultanova N. Subgradient method for nonconvex nonsmooth optimization // Journal of Optimization Theory and Applications. 2013. V. 157, no. 2. P. 416-435.
24. Beck A., Teboulle M. Smoothing and first order methods: a unified framework // SIAM Journal of Optimization. 2012. V. 22, no. 2. P. 557-580.
25. Сулимов В.Д. Локальная сглаживающая аппроксимация в гибридном алгоритме оптимизации гидромеханических систем // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2010. № 3. С. 3-14.
26. Сулимов В.Д., Шкапов П.М. Глобальная минимизация многомерной многоэкстремальной липшицевой целевой функции с использованием гибридного алгоритма V-PCALMS: Свидетельство о государственной регистрации программы для ЭВМ № 2012617546. 2012.
27. Price C.J., Coope I.D., Byatt D. A convergent variant of the Nelder-Mead algorithm // Journal of Optimization Theory and Applications. 2002. V. 113, no. 1. P. 5-19.
28. Sulimov V.D., Shkapov P.M. Application of hybrid algorithms to computational diagnostic problems for hydromechanical systems // Journal of Mechanics Engineering and Automation. 2012. V. 2, no. 12. P. 734-741.
Публикации с ключевыми словами: глобальная оптимизация, гидромеханическая система, экстремальная задача, липшицева функция, критериальная функция, локальный поиск, гибридный алгоритм
Публикации со словами: глобальная оптимизация, гидромеханическая система, экстремальная задача, липшицева функция, критериальная функция, локальный поиск, гибридный алгоритм
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



