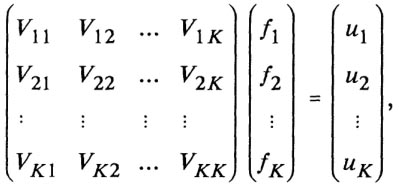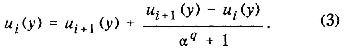научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#9 сентябрь 2006
DOI: 10.7463/0906.0060408
А.П. Карпенко, д-р физ.-мат. наук проф., МГТУ им. Н.Э. Баумана
В настоящее время кардинально ускорить исследования, связанные с моделированием на ЭВМ, можно только путем использования многопроцессорных вычислительных систем (МВС). Кроме высокой скорости вычислений другими важными достоинствами МВС являются их более низкая удельная скорость, повышенная надежность и живучесть, способность к постепенному наращиванию вычислительной мощности по сравнению с однопроцессорными ЭВМ. Для эффективного использования МВС требуется решить ряд задач, среди которых одной из важнейших является задача согласования (mapping или matching problem) [1]. В соответствии с тем, что распараллеливание может быть осуществлено на уровнях построения модели исследуемого явления, метода решения, алгоритма и программы [2], можно говорить о согласовании на уровнях модели, метода, алгоритма, программы и вычислительного процесса. Согласование на уровне алгоритма предполагает, что модель и метод исследования фиксированы. Требуется среди множества алгоритмов, соответствующих им, найти наилучший для данной МВС по заданному критерию эффективности согласования. Методы и алгоритмы, используемые при решении задачи согласования, существенно зависят от того, какой параллелизм имеется в виду — "мелкозернистый" или "крупнозернистый" [3]. Статья ориентирована на "крупнозернистый" параллелизм (параллелизм на уровне ветвей алгоритма), который адекватен МВС с архитектурой MIMD. Множество алгоритмов, на котором решается задача согласования, в тривиальном случае представляет собой просто набор различных алгоритмов. В этом случае задача согласования является переборной — для каждого алгоритма требуется, вообще говоря, решить задачу согласования на уровне программы и выбрать алгоритм, который обеспечивает оптимальное значение критерия эффективности согласования. В статье в качестве указанного множества алгоритмов рассматривается множество алгоритмов А, порожденных изменением некоторого вектора параметров К: А = {А(K), К Î К}, где К — множество допустимых значений К. В этом случае задача согласования (параметрического) есть задача поиска вектора параметров K* Î К ( а тем самым и алгоритма А(К*)), оптимизирующего заданный критерий эффективности согласования. В некоторых случаях задача параметрического согласования может быть решена без полного перебора векторов из множества К, а в простейших случаях — аналитически. Строгая постановка задачи параметрического согласования дана в работе [4]. Идея построения параметрического множества алгоритмов и поиска в нем оптимального для данной МВС алгоритма впервые, вероятно, высказана в работах [5, 6]. Упоминание о возможности подобного использования параметризованных множеств параллельных алгоритмов имеется также в работе [7]. В данной статье для построения параметризованных множеств алгоритмов используется методика, основанная на комбинации метода декомпозиции области решения до и после дискретизации задачи и ускоряющих преобразований на основе многосеточных методов. Методика предложена нами совместно с Ю.П. Боглаевым в работе [8]. Методика порождает множества, вообще говоря, трехуровневых иерархических алгоритмов, параметрами которых являются порядок ускоряющего преобразования и количество подобластей [9—11]. Указанная методика использована нами для построения параметризованных множеств следующих алгоритмов: 1) вычисления кубатур [9]; 2) интерполяции на основе локальных и нелокальных кубических сплайнов [10]; 3) интегрирования одного класса обыкновенных дифференциальных уравнений [11]. В качестве примера рассмотрим использование этой методики для задачи интерполяции на основе нелокальных кубических сплайнов. Программная реализация идеи параметрического согласования приводит к "гибкой" программе [12], параметрически самосогласующейся с архитектурой используемой вычислительной системы Такая программа на основе информации о вычислительной сложности задачи, допустимой погрешности решения и архитектуре вычислительной системы определяет оптимальные вектор параметров К* и алгоритм А(K)* и реализует найденное оптимальное или квазиоптимальное отображение программы, соответствующей алгоритму А(K)*, на данную архитектуру. В статье рассматривается пример реализации параметризованного алгоритма интерполяции на основе нелокальных кубических сплайнов в виде программы, параметрически самосогласующейся с архитектурой вычислительной системы ПС-3000 [13]. МЕТОДИКА СИНТЕЗА ПАРАМЕТРИЗОВАННЫХ АЛГОРИТМОВ. Изложим методику параметризации на примере прямой задачи численного анализа. Пусть L(W) — пространство функций f(x) с нормой || . ||W, определенных на множестве W Ì Rn. Линейный оператор V действует из L(W) в пространство L(w) функций u(y) с нормой || . || w, определенных на множестве w и имеющих значения в пространстве R1, т.е. Vf = u. (1) Рассмотрим задачу приближенного построения функции u(y) по заданной функции f(х). Строгая постановка задачи дана в работе [8]. Методика основана на так называемых прямом, блочном и ускоряющем методах синтеза параллельных алгоритмов. Прямой метод. Проведем дискретизацию множеств W, w и обозначим полученные множества
Разобьем множества Прямой метод распараллеливания включает в себя два этапа: • параллельное вычисление значений решения на множествах • построение на основе найденных значений приближенного решения u(у) Î L(w) ("сборка" решения). Параметром численного алгоритма, полученного на основе прямого метода, является количество подмножеств К. Очевидно, что прямой метод есть ни что иное, как широко используемая в вычислительной практике геометрическая схема распараллеливания соответствующего последовательного алгоритма. Поэтому погрешность прямого алгоритма равна погрешности последнего. Далее прямой метод не рассматривается. Блочный метод. Разобьем множества W, w на К непересекающихся подмножеств Wi, wi, i Î [1, К]. Эти разбиения порождают [8] разложение пространств L(W), L(w) в прямую сумму подпространств L(Wi), L(wi) и блочное представление (1):
где fi Î L(Wi), ui Î L(wi). Блочный метод распараллеливания состоит из двух следующих шагов. • параллельное вычисление ui = Vl,1f1 + Vi,2f2 + ... + Vi,KfK, i Î [1, K]; • построение на основе найденных значений ui приближенного решения (1). Параметром численного алгоритма, полученного на основе блочного метода, является количество подмножеств К. Ускоряющий метод. Этот метод основан на применении ускоряющих преобразований Ричардсона, Эйткена, Шенкса и др. [14]. Изложим схему метода на примере преобразования Ричардсона. Пусть Wi , i = 1, 2, ... есть последовательность дискретизаций множества W такая, что lim ||Wi|| = 0, i ® 0 где || . || есть некоторая норма в Rn. Найдем приближенное решение задачи (1) ui(у) Î L (w). Если погрешность приближения u(у) функцией ui(у) может быть представлена в виде ||u(y) - ui(y)||w= c ||Wi||q + O (||Wi||q+1), где q > 0, с — неизвестная константа, то ускоряющее преобразование Ричардсона для функций ui(у), ui+1(у) задается формулой
Здесь a = ||Wi+1|| / ||Wi||. Погрешность приближения u(у) функцией ui(у) равна ||u(у) - ui(у)||w = О(|| Wi ||)q+1). Схема ускоряющего метода распараллеливания на основе преобразования Ричардсона имеет вид: • параллельное нахождение решений ui(y); ui+1(у); • "сборка" по формуле (3) уточненного решения. Количество параллельных ветвей К в данном случае равно двум. Большим потенциальным параллелизмом обладают известные обобщения преобразования Ричардсона, использующие при формировании и) (у) не только решения а,(у), и^/у), но и решения и*2<У). и^3(у) и т.д. СИНТЕЗ ПАРАМЕТРИЗОВАННОГО МНОЖЕСТВА АЛГОРИТМОВ ОДНОМЕРНОЙ ИНТЕРПОЛЯЦИИ НА ОСНОВЕ НЕЛОКАЛЬНЫХ КУБИЧЕСКИХ СПЛАЙНОВ. Постановка задачи. Рассматривается функция f(x), х Î [а, b] одного переменного из класса функций С1(m) (Мт) = С(т)(Мт). Решается задача построения непрерывной на [а, b], возможно со своей первой и старшими производными, функции F(x), интерполирующей f(х) на сетке D : а = x0< х1 < х2...<хn = b, где хi — xi-1 = hi, i Î [1, n] — шаг сетки (рис. 1). Функция F(x) строится на основе непериодических нелокальных кубических сплайнов с краевыми условиями вида W(x0) = W0 = f(1)(x0), W(xn) = Wn = f(1)(xn), где W0, Wn — "наклоны" в узлах х0, хn сетки D [15]. Погрешность приближения f(х) функцией F(х) оценивается величиной || R(x) || = sup | f(x) - F(х)|. х Î [а,b] Наряду с сеткой D используется сетка D', содержащая 2n + 1 узлов (рис. 1). Заметим, что все результаты могут быть перенесены на случай периодического сплайна, задания сплайна через "моменты", и отличные от рассматриваемых краевые условия [15]. Блочный алгоритм. Схема блочного алгоритма построения функции F(х) имеет вид: 1) разбиение интервала [а, b] по узлам сетки D на К подынтервалов [аi, bi], i Î [1, К] и К— 1 подынтервалов [a'i, b'i], i Î [1, K- 1] (рис. 2); 2) параллельное построение на интервалах [ai, bi] нелокальных кубических сплайнов Si(x) с краевыми условиями Si(j)(ai) = f(j)(ai), Si(j)(bi) = f(j)(bi), где j = О, 1.
3) параллельное построение на vi + 2 узлах каждого из подынтервалов [а'i, b'i], i Î [1, К — 1] интерполирующих полиномов Эрмита Еi(х) порядка vi + 5 с краевыми условиями
где j= 0, 1, 3; 4) "сборка" искомой функции
Ограничимся случаем v = 0. При этом порядок интерполирующего полинома Эрмита равен 5. В работе [10] показано, что если f(x) Î С(m)(Мm), m ³ 1, то функция F(х), построенная на основе нелокального кубического сплайна S(x) и локального сплайна пятого порядка Е(х) с помощью блочного алгоритма: 1) принадлежит классу С(3)[а, b], 2) совпадает в узлах сетки D с соответствующими значениями функции f(х), 3) приближает f(х) с погрешностью
1) построение сеток D, D' (см. рис. 1); 2) параллельное определение на этих сетках интерполирующих нелокальных кубических сплайнов S(x), S' (х); 3) "сборка" искомой функции F(x) = S'(x) + (S(x) - S'(x)) r (x), где функция r(х) определяется главными членами погрешностей приближения f(х) сплайнами S(х), S'(x). В работе [10] показано, что если /(х) е С(т)(Мт), т * 5, то функция Р(х), построенная с помощью ускоряющего алгоритма на основе преобразования Ричардсона: 1) принадлежит классу С(2)[а, b]; 2) совпадает в узлах сетки D ' с соответствующими значениями функции f(х); 3) приближает f(х) с погрешностью || R(x) || £ 3/8 aM5H5; где
Н — шаг сетки D. Заметим, что если f(х) Î С(m)(Мm), m ³ 5, то ускоряющий алгоритм на основе преобразования Ричардсона по сравнению с нелокальным кубическим сплайном $(х) обладает следующими свойствами: • на единицу относительно Н повышает порядок приближения f(х) функцией F(х); • на единицу повышает порядок гладкости функции f(х), при котором происходит насыщение интерполяционного процесса. Существенным является тот факт, что функция F(х), построенная с помощью ускоряющего алгоритма на основе преобразования Ричардсона, не обладает основным свойством нелокальных кубических сплайнов — непрерывностью второй производной. Причиной этого, легко видеть, является разрывность первой производной функции r(х) в узлах сетки D. В работе [10] предложена модификация r(х), при которой F(х) принадлежит классу С(3)[а, b], и исследованы некоторые другие свойства функции F(х). Замечание. Мы показали, что ускоряющий алгоритм на основе преобразования Ричардсона, использующий нелокальные кубические сплайны, повышает порядок приближения лишь для функций, более гладких, чем функции класса f(х) Î С(4)(М4). Это обстоятельство делает нецелесообразным применение ускоряющего алгоритма на основе преобразования Ричардсона к функциям, построенным с помощью блочного алгоритма в предыдущем пункте. Таким образом, результаты исследования позволяют строить двухуровневые алгоритмы одномерной интерполяции, использующие прямой и блочный либо прямой и ускоряющий алгоритмы. ПРИМЕР РЕАЛИЗАЦИИ. На основе предложенного подхода разработаны параметрически самосогласующиеся программы для ряда МВС, реализующие рассмотренные блочный и/или ускоряющий алгоритмы одномерной интерполяции на основе нелокальных кубических сплайнов: 1) программа для двухпроцессорной вычислительной системы NORD 10/50 (блочный и ускоряющий алгоритмы) [16]; 2) программа для вычислительной системы ПЭВМ ЕС 1840 — параллельный сопроцессор ПСП (блочный алгоритм) [17]; 3) программа для вычислительной системы ПС-3000 с одним скалярным и одним векторным процессорами (блочный алгоритм) [13]. Рассмотрим последнюю программу [18]. Алгоритм параметрического согласования, реализованный в программе, ориентирован на критерий эффективности, возрастающий по К, k, (k — количество узлов в каждом из К блоков) и погрешность R (F) приближения f(х) функцией F(х), убывающую по тем же параметрам. Алгоритм состоит в выборе (путем перебора) из допустимых К, k, при которых R(F) £ e, значений, доставляющих локальный минимум критерию эффективности согласования. Здесь e — максимально допустимая погрешность интерполяции. Рассматривается два отображения алгоритма на архитектуру МВС: отображение Х1, при котором все вычисления выполняются на скалярном процессоре; отображение Х2, при котором вычисление значений интерполируемой функции и построение интерполирующих сплайнов и полиномов Эрмита в блоках выполняются на векторном процессоре, а построение интерполирующей функции F(х) (ее "сборка") — на скалярном процессоре. В последнем случае вычисления в соседних блоках выполняются на соседних процессорах векторного процессора. Используемый критерий эффективности согласования представляет собой время построения интерполирующей функции и учитывает особенности архитектуры МВС ПС-3000:
где pf — вычислительная сложность функции f(х); a1, a2 — экспериментально определенные константы; q1, q2 — производительности скалярного и векторного процессоров, соответственно; [v] — ближайшее целое, большее v. Погрешность приближения f(х) функцией F(х) оценивается суммой взвешенных величин R(S), R(Е) — погрешностей приближения f(х) на блоке нелокальным кубическим сплайном и полиномом Эрмита пятого порядка, соответственно:
Здесь К(k — 1) и K — 1 — количество шагов сетки, на которых }(х) приближается нелокальными кубическими сплайнами и полиномами Эрмита, соответственно, Кk — 1 — общее число шагов. С помощью рассматриваемой программы мы выполнили исследование эффективности параметрического согласования В качестве интерполируемой функции f(x) использовалась функция с порядком гладкости m = 3, имеющая производную f(3)(x), ограниченную величиной m3 = 240 Максимально допустимая погрешность интерполяции е принималась равной 24 . 10-4. Использовались следующие ограничения на параметры К: k ³ 3,1 £ К £ 50,Кk= 250, т е число блоков могло изменяться от 1 до 50, а суммарное количество узлов в сетке ограничивалось 250 Так как при каждом данном количестве блоков оптимальным, очевидно, является алгоритм, имеющий минимальное число узлов в них, то эксперименты проводились при тех К, k, при которых R(F) = e. Результаты исследования показывают, что для всех рассмотренных вычислительных сложностей интерполируемой функции рf оптимальным является отображение Х2 (с использованием векторного процессора) Время решения задачи уменьшается при этом до 7 раз по сравнению с отображением Х1 (без его использования). Для отображения X1 независимо от pf оптимальным является число блоков К = 1 и число узлов k = 169 Объясняется это тем, что при данных значениях К, k: минимально суммарное количество узлов в сетке Для отображения Х2 оптимальные значения параметров К, k зависят от вычислительной сложности интерполируемой функции. С уменьшением рf оптимальное число блоков К возрастает до ~15, а число узлов k в каждом из них уменьшается до ~12 Этот результат является следствием двух противоположных тенденций: с одной стороны, с ростом числа блоков увеличивается общее число узлов в сетке и, тем самым, общий объем вычислительной работы; с другой стороны, с ростом К увеличивается уровень параллелизма алгоритма и эффективность использования векторного процессора. Выигрыш в значении критерия эффективности согласования может достигать 5 раз Список литературы 1 Воеводин В.В. Математические модели и методы в параллельных процессах М • Наука, 1986 296 с 2 Молчанов И.Н. Введение в алгоритмы параллельных вычислений Киев Наукова думка, 1990 128 с 3 Gruber R., Cooper W.A., Beniston M., Gengler M. Software development strategies for parallel computer architectures // Physics Report (Review Section of Physics Letters) 1991. V.207 N3—5 Р 167-214 4 Карпенко А.П. Параметрическое согласование вычислительных алгоритмов с архитектурой многопроцессорных систем / 1. Общий случай М , 1993 25 с. (Препринт/ИВТАН; N 2—367). 5 Давыдов Ю.М. Дифференциальные приближения и представления разностных схем М МФТИ, 1981 131 с. 6. Давыдова И.М., Давыдов Ю.М. Об особенностях решения вычислительных задач на современных и перспективных высоко производительных вычислительных системах // Вычислительные процессы и системы (Москва). 1985. N 2. С. 162—172. 7. Миренков Н.Н. Параллельное программирование для много модульных вычислительных систем. М.: Радио и связь, 1989. 320 с. 8. Bogaev Yu.P., Karpenko A.P. Hierarchy of parallelism in some problems of numerical analysis. Chernogolovka, 1988. 19p.(Preprint/Institute of Solid State Physics). 9. Боглаев Ю.П., Карпенко А.П. Иерархия параллельных вычислений кубатур. Черноголовка, 1986. 22 с. (Препринт/ИФТТ АН СССР). 10. Боглаев Ю.П., Карпенко А.П. Некоторые алгоритмы интерполяции на основе одномерных сплайнов для многопроцес сорных вычислительных систем. Черноголовка, 1987. 36 с. (Пре принт/ ИФТТ АН СССР). 11. Карпенко А.П. Методы интегрирования линейных обыкно венных дифференциальных уравнений второго порядка, ориенти рованный на многопроцессорные вычислительные системы. М , 1990. 33 с. (Препринт/ ИВТАН; N 8-306). 12. Schwan K., Jones A.K. Flexible software development for multiple computer system // IEEE Trans. on Software Eng. - 1986. VSE12, N 3. P. 385-401. 13. Карпенко А.П., Шумаева С.М. Одномерная сплайн-интер поляция, самосогласующаяся с архитектурой вычислительной системы ПС-3000 // Информ. бюлл. "Алгоритмы и программы" / ВНТИЦентр. М., 1990. N 2. С. 7. (Рег. номер ГосФАП 50890000528). 14. Марчук Г.И., Шайдуров В.В. Повышение точности реше ний разностных схем. М.: Наука, 1979. 240 с. 15. Алберг Дж., Нильсон Э., Уолш Дж. Теория сплайнов и ее приложения. М.: Мир, 1973. 230 с. 16. Карпенко А.П., Шумаева С.М. Программа одномерной сплайн-интерполяции, самосогласующаяся с архитектурой двух процессорной вычислительной системы МОКВ 10/50// Информ. бюлл. "Алгоритмы и программы" / ВНТИЦентр. 1990. N 1. С. 6 (Рег. номер ГосФАП 50890000404). 17. Одномерная сплайн-интерполяция, самосогласующаяся с архитектурой вычислительной системы ПЭВМ ЕС 1840 / парал лельный сопроцессор ПСП / А.П. Карпенко, В.М. Кузьмицкий, А.С. Липницкий и др. // Информ. бюлл. "Алгоритмы и програм мы" / ВНТИЦентр. 1989. N11. С. 4. (Рег. номер ГосФАП 50880000075). 18. Боглаев Ю.П., Карпенко А.П., Шумаева С.М. Параметри ческое согласование некоторых алгоритмов сплайн-интерполяции с архитектурой многопроцессорных вычислительных систем // Автоматика и телемеханика. 1990. N 5. С. 166—176.
|
Публикации с ключевыми словами: вычислительные алгоритмы, многопроцессорные системы
Публикации со словами: вычислительные алгоритмы, многопроцессорные системы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||