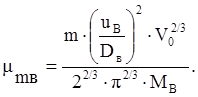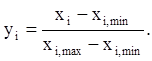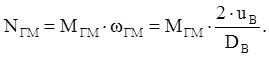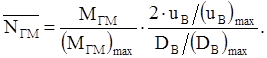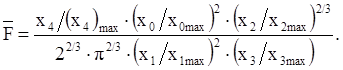научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 07, июль 2013
DOI: 10.7463/0713.0590873
Россия, МГТУ им. Н.Э. Баумана
Введение
Для решения задачи выбора оптимальных параметров технических систем существует несколько хорошо зарекомендовавших себя методов. Широкое применение получили методы, основанные на использовании множества Парето[1-3], и связанный с ними ЛПτ-поиск оптимальных параметров [4]. Основная особенность данных методов состоит в том, что конструктор по результатам численных экспериментов выбирает наилучший вариант, основываясь на своем опыте. При этом конструктор имеет возможность в интерактивном режиме учитывать неформализуемые критерии качества системы.
В последнее время при решении задач оптимального проектирования технических систем обращается внимание на трудоемкость используемого метода. Основанные на генетических алгоритмах (далее ГА) и модифицированных генетических алгоритмах (далее МГА) методы, позволяют сократить объем вычислений и найти оптимальные параметры системы [5, 6].
Для системы охлаждения двигателя транспортного средства большой грузоподъемности предварительно была выбрана схема гидропривода с дискретным гидрораспределителем [7]. Описывающая динамику данной системы математическая модель представлена в работе [8]. Результаты математического моделирования и физического эксперимента показали, что оптимальные переходные процессы обеспечиваются настройкой клапанов управления гидрораспределителя и поэтому не нужно применять дополнительные устройства для корректирования динамики выбранной системы гидропривода [8, 9]. Необходимо оптимизировать при выборе только параметры, выпускаемых фирмами элементов, которые используются в гидроприводе.
Для выбора целевой функции при решении задачи проектирования оптимальной системы следует предварительно определить показатели ее качества. Число показателей качества при оценке эффективности проектного варианта гидропривода целесообразно, по возможности, ограничивать. Численные значения показателей качества могут быть назначены так, что лучшему проектному варианту будут соответствовать максимальные значения одних и минимальные значения других.
Массогабаритные показатели и энергетические характеристики обычно публикуются фирмами-изготовителями элементов гидропривода. Они широко используются в практике проектирования технических систем. Для сравнения проектных вариантов лучше применять безразмерные показатели, вычисляемые в виде некоторых чисел подобия. В случае гидропривода с неограниченным по углу вращательным движением выходного звена такое число определяет формула [10]
| (1) |
в которой m – масса всего устройства вместе с рабочей жидкостью, Ωв – угловая скорость выходного звена, q – характерный объем гидромотора, равный 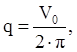 где V0 – рабочий объем гидромотора, Mв – максимальный вращающий момент, действующий на выходное звено. Индексы “m” и “в” указывают на связь числа с массой и вращательным движением выходного звена устройства, соответственно.
где V0 – рабочий объем гидромотора, Mв – максимальный вращающий момент, действующий на выходное звено. Индексы “m” и “в” указывают на связь числа с массой и вращательным движением выходного звена устройства, соответственно.
Входящие в формулу (1) величины зависят от конструкции и размеров элементов гидропривода, что исключает возможность указать зависимости этих величин друг от друга. При решении задачи выбора параметров гидропривода для системы охлаждения двигателя транспортного средства необходимо найти такой проектный вариант, чтобы предложенная в виде (1) целевая функция имела бы минимальное значение.
Для вычисления параметров гидропривода в проектном варианте, заменим в формуле (1) величину Ωв диаметром Dв рабочего колеса вентилятора и его окружной скоростью uв на радиусе Dв/2. В результате получим
| (2) |
При применении генетических алгоритмов, необходимо формулу (2) преобразовать, представив совокупность варьируемых параметров в виде
| (3) |
где x0 ≡ uв (м/с), x1 ≡ Dв (м), x2 ≡ V0 (м3), x3 ≡ Mв (Нм), x4 ≡ m (кг)..
С помощью (3) формулу (2) можно представить как
| (4) |
2. Применение МГА при решении задачи
Сначала заменим в формуле (4) переменные x0, x1, x2, x3, x4, нормированными параметрами [11]:
| (5) |
В соотношении (5), хi– варьируемое значение параметра, а xi,maxи xi,min– максимальное и минимальное значения параметра, соответственно.
Ограничения варьируемых при выборе оптимальных параметров системы примем, исходя из каталогов фирм-изготовителей гидрооборудования и рекомендаций в практике ее использования. Эти ограничения как начальные xнач и конечные xкон значения параметров следующие:
| (6) |
После применения соотношения (5) к совокупности ограничений на варьируемые параметры (6), нормированные ограничения примут вид
|
|
Применяя алгоритм МГА [12], получили значения совокупности нормированных параметров:
|
|
3. Применение ГА при решении задачи
Рассмотренная задача выбора параметров системы с гидроприводом была решена также с помощью встроенного в MatlabГА [6, 13, 14]. В результате получили
|
|
4. Решение задачи с помощью ЛПτ-поиска
Для оценки результатов решения задачи по выбору параметров с помощью одного глобального критерия, используемого в генетическом алгоритме, был применен ЛПτ-поиск при двух критериях: решающего [4] – функции вида (4) и мощности, развиваемой гидромотором.
Полученные выше решения параметров исследуемой системы доставляют минимум одному критерию (4), который вследствие этого является решающим. Чтобы выяснить, потребуется ли варьировать значения параметров, если независимо от критерия (4) изменять полезную мощность гидромотора, был использован ЛПτ-поиск для определения оптимальных параметров системы в соответствии с принципом Парето.
Размерное значение мощности, развиваемой гидромотором Nгм, определяет соотношение:
| (7) |
Для дальнейшего исследования результатов оптимизации параметров системы представим соотношение (7) в безразмерной форме:
|
|
В этом случае
|
|
Критерием оптимальности служит минимальное расстояние выбранной точки в пространстве нормированных критериев от начала координат.
Найденному значению соответствует точка в пространстве размерных параметров, определяемая совокупностью (3):
|
|
Результаты оптимизации системы приведены на рисунке 1.

Рис. 1. Результаты определения оптимальных параметров системы с гидроприводом различными способами.
4. Сравнение результатов определения оптимальных параметров тремя способами с выбранными параметрами при интерактивном проектировании системы
При проектировании рассматриваемой системы, кроме целевой функции и параметрических ограничений, требовалось учитывать такие неформализуемые условия, как возможности использования в гидроприводе реально существующих элементов. Вследствие этого, окончательно были приняты параметры вентилятора и гидромотора, указанные в последней строке таблицы 1. Полученные в результате оптимизации параметры системы приведены в первых строках таблицы 1.
Таблица 1. Параметры системы охлаждения двигателя транспортного средства
Параметры Способ определения | uв, м/с | Dв, мм | V0, см3 | Mв, Нм | m, кг |
Значения параметров, полученных при использовании ГА с помощью одного глобального критерия | 70,00 | 631,9 | 21,90 | 71,39 | 8,16 |
Значения параметров, полученных при использовании МГА с помощью одного глобального критерия | 70,00 | 625,9 | 23,20 | 70,54 | 8,20 |
Значения параметров, полученных при использовании принципа Парето с применением ЛПτ-поиска по двум критериям | 75,283 | 671,3 | 21,46 | 72,24 | 8,65 |
Значения параметров, принятые с учетом неформализуемых критериев и используемых в разработанной системе с гидроприводом | 74,88 | 650,0 | 26,00 | 70,4 | 8,82 |
При указанных в таблице 1 значениях параметров uв, Dв, Mв полезная мощность гидромотора, вычисленная с помощью формулы (7), приведена в таблице 2.
Таблица 2. Полезная мощность гидромотора
Способ определения значения мощности | Значение мощности гидромотора, кВт |
Получено при использовании ГА | 15,82 |
Получено при использовании МГА | 15,78 |
Получено при использовании принципа Парето с применениемЛПτ-поиска | 16,20 |
Значение, принятое в результате интерактивного проектирования системы | 16,25 |
Заключение
Использование генетических алгоритмов (ГА и МГА) в задачах проектирования гидроприводов с дискретно управляемым движением выходного звена позволяет находить оптимальное проектное решение по основанной на формуле (1) одной целевой функции.
Рассмотренные в статье три способа выбора оптимальных параметров системы дают близкие значения параметров, но решение задачи с помощью ЛПτ-поиска с двумя критериями является более трудоемким, чем решение с помощью генетических алгоритмов. В связи с этим, последний способ следует применять на заключительном этапе интерактивного проектирования при необходимости учета неформализуемых критериев.
Полезная мощность гидромотора, полученная при интерактивном проектировании системы, несколько превышает оптимальное значение, но обеспечивает создание гидропривода из стандартно выпускаемых фирмами изделий. Испытания опытного образца такого гидропривода подтверждают целесообразность его применения.
Список литературы
1. Боровин Г.К., Попов Д.Н. Многокритериальная оптимизация гидросистем: учеб. пособие для вузов. М.: МГТУ им. Н.Э. Баумана, 2007. 94 с.
2. Карпенко А.П., Семенихин А.С. Аппроксимации множества Парето методами роя частиц и муравьиной колонии // 6-я международная научно-практическая конференция "Интегрированные модели и мягкие вычисления в искусственном интеллекте" (Коломна, 16-19 мая 2011 г.): тез. докл. Коломна, 2011. С. 83-94.
3. Воронов Е.М. Многокритериальный синтез позиционного управления на основе многопрограммной стабилизации. Ч. 1 // Вестник МГТУ им. Н.Э. Баумана. Сер. Приборостроение. 2012. № 2. С. 3-19.
4. Соболь И.М., Статников Р.Б. Выбор оптимальных параметров в задачах со многими критериями. М.: Дрофа, 2006. 176 с.
5. Генетические алгоритмы, искусственные нейронные сети и проблемы виртуальной реальности / Г.К. Вороновский, К.В. Махотило, С.Н. Петрашев, С.А. Сергеев. Харьков: Основа, 1997. 112 с.
6. Панченко Т.В. Генетические алгоритмы: учеб. пособие. Астрахань: Издательский дом «Астраханский университет», 2007. 88 с.
7. Труханов К.А. Гидропривод вентилятора для системы охлаждения автомобильного двигателя // Известия МГТУ «МАМИ». 2011. № 2 (12). С. 78-84.
8. Труханов К.А. Математическое моделирование гидропривода вентилятора для системы охлаждения автомобильного двигателя // Известия МГТУ «МАМИ». 2012. № 1 (13). С. 84-95.
9. Кригер А.М., Дискин М.Е., Новенников А.Л., Пикус В.И. Жидкостное охлаждение автомобильных двигателей. М.: Машиностроение, 1985. 176 с.
10. Попов Д.Н. Оценка эффективности и оптимальное проектирование гидроприводов // Вестник машиностроения. 1986. № 9. С. 20-23.
11. Ежов А.А., Шумский С.А. Нейрокомпьютинг и его применения в экономике и бизнесе. Режим доступа: http://www.intuit.ru/department/expert/neurocomputing/7/3.html (дата обращения 21.12.2012).
12. Смирнов Н.И., Сабанин В.Р., Репин А.И. Модифицированный генетический алгоритм для задач оптимизации в управлении. Режим доступа: http://www.neuroproject.ru/Papers/exponenta.doc (дата обращения 08.10.2012).
13. Constrained Minimization Using the Genetic Algorithm // MathWorks : website. Режим доступа: http://www.mathworks.com/help/gads/examples/constrained-minimization-using-the-genetic-algorithm.html (дата обращения 22.11.2012).
14. Открытие инструментария генетического алгоритма // MATLAB.Exponenta : сайт. Режим доступа: http://matlab.exponenta.ru/genalg/08_03_01.php (дата обращения 04.03.2013).
Публикации с ключевыми словами: гидропривод, оптимизация, двигатель, система охлаждения, вентилятор, параметры оптимальные, средство транспортное, управление дискретное, функция целевая
Публикации со словами: гидропривод, оптимизация, двигатель, система охлаждения, вентилятор, параметры оптимальные, средство транспортное, управление дискретное, функция целевая
Смотри также:
- Оптимизация среднеоборотного дизеля с наддувом при ограничении максимального давления цикла.
- Проблемы оптимального проектирования гидропривода вентилятора для системы охлаждения автомобильного двигателя
- Выбор хладагента и оптимизация параметров цикла системы термостатирования посадочного аппарата «Венера-Д»
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||