научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 07, июль 2013
DOI: 10.7463/0713.0590785
УДК 004.942, 519.876.5
Россия, МГТУ им. Н.Э. Баумана
Введение
При решении задач математической физики численными методами, такими как метод конечных элементов [1], метод конечных разностей [2], часто возникает необходимость нахождения решения систем линейных алгебраический уравнений (СЛАУ) [3] высоких порядков, матрица коэффициентов которых имеет выраженный диагональный (ленточный) характер. С распространением многопроцессорных вычислительных систем появилась возможность адаптации точных алгоритмов решения СЛАУ к данной архитектуре. Работы в этом направлении ведутся продолжительное время [4], разработано большое количество алгоритмов для вычислительных систем различной архитектуры [5-7]. Однако, предложенные алгоритмы рассматривают диагональную ленту матрицы коэффициентов как полностью заполненную ненулевыми элементами, хотя в практических задачах эта лента, как правило, содержит большое количество ненулевых диагоналей. Поэтому актуальной является задача разработки алгоритма, учитывающего внутреннюю разреженность диагональной ленты матрицы коэффициентов, что должно повысить его экономичность.
В работе предложен алгоритм параллельного решения СЛАУ с многодиагональной (многоленточной) матрицей коэффициентов на многопроцессорной вычислительной системе с общей памятью. Данный алгоритм реализует метод Гаусса [3] и состоит из трёх основных этапов: трансформация задачи, прямой ход алгоритма, обратный ход алгоритма.
1. Постановка задачи
Задача нахождения решения СЛАУ может быть представлена в виде
![]() x = c, (1)
x = c, (1)
где A - квадратная ленточная матрица коэффициентов с шириной ленты L, x - вектор-столбец неизвестных, с – вектор-столбец свободных членов. В общем случае A, x и c имеют вид
| | | | | | | | |
| | | | | | | | (2) |
| | | | , | | , | | . |
Под решением задачи понимают такую совокупность чисел ![]() , которая при подстановке на место неизвестных
, которая при подстановке на место неизвестных ![]() обращает все уравнения этой системы в тождества. Для большинства практических задач определитель матрицы A отличен от 0, следовательно, задача (1) имеет единственное решение.
обращает все уравнения этой системы в тождества. Для большинства практических задач определитель матрицы A отличен от 0, следовательно, задача (1) имеет единственное решение.
Следует отметить следущую особенность решения СЛАУ с ленточной матрицей коэффициентов. Исходная матрица в практических задачах является сильно разреженной, однако, в ходе решения прямыми методами (таким, например, как метод Гаусса) лента полностью заполняется новыми ненулевыми элементами, что резко замедляет ход как последовательного, так и параллельного решения.
2. Трансформация задачи
На данном этапе производится изменение задачи (1) с целью уменьшения количества новых ненулевых элементов матрицы коэффициентов и упрощения процедуры распределения нагрузки между процессорами вычислительной системы.
Пусть N - число диагоналей, содержащих отличные от нуля элементы матрицы A(ненулевые диагонали),![]() - вектор, содержащий элементы k-ой ненулевой диагонали. Размерность векторов dk постоянна и равна n. Индексы компонентов векторов
- вектор, содержащий элементы k-ой ненулевой диагонали. Размерность векторов dk постоянна и равна n. Индексы компонентов векторов ![]() соответствуют индексам строк матрицы A, в которых они находятся. Если какой-либо компонент векторов
соответствуют индексам строк матрицы A, в которых они находятся. Если какой-либо компонент векторов ![]() выходит за пределы матрицы A, то данные компоненты тождественно равны 0. Будем считать, что диагональ матрицы A, представленная вектором d1,не содержит нулевых элементов.
выходит за пределы матрицы A, то данные компоненты тождественно равны 0. Будем считать, что диагональ матрицы A, представленная вектором d1,не содержит нулевых элементов.
Введем смещение ![]() – натуральное число, лежащее в интервале
– натуральное число, лежащее в интервале ![]() . Значение
. Значение ![]() определяется по формуле
определяется по формуле
![]()
Расширим вектор xзадачи (1), добавив в его начало Sпеременных, а также введём в систему ![]() дополнительных уравнений
дополнительных уравнений

где ![]() - неизвестные, добавленные в (1). Введённым уравнениям присвоим номера
- неизвестные, добавленные в (1). Введённым уравнениям присвоим номера ![]() . Тогда модифицированная задача примет вид
. Тогда модифицированная задача примет вид
![]() x` = c`, (3)
x` = c`, (3)
где A` - матрица коэффициентов, x` - вектор-столбец неизвестных и с` - вектор-столбец свободных членов. Размерность матрицы ![]() составит
составит ![]() , размерности векторов x` и c` будут равны
, размерности векторов x` и c` будут равны ![]()
Далее к строкам матрицы  с индексом
с индексом  прибавим строки матрицы
прибавим строки матрицы  , полученные после модификации (1), по следующему правилу –
, полученные после модификации (1), по следующему правилу –
к строке с индексом  прибавляется строка с индексом
прибавляется строка с индексом  .
.Рассмотрим пример трансформации исходной задачи (1) размерности 5x5 со смещениеми
. Исходная задача имеет вид
| | | | | * | | | | | (4) | |
| 0 | | 0 | 0 | | | | | |||
| | | | ||||||||
0 | | 0 | | 0 | |||||||
| = | | | ||||||||
| 0 | | 0 | | |||||||
| | | | ||||||||
0 | | 0 | | 0 | |||||||
| | | . | ||||||||
0 | 0 | | 0 | |
Отметим, что в данной задаче D= (d1, d2, d3). Модифицируем задачу, используя рассмотренный выше алгоритм.
Так как S = 2, добавим две дополнительные переменные и два уравнения в задачу (4):
| | | | | | | * | | | |
| |
0 | 0 | | 0 | | 0 | 0 | | | | |||
| | | ||||||||||
0 | 0 | 0 | | 0 | | 0 | ||||||
| | | ||||||||||
0 | 0 | | 0 | | 0 | | ||||||
| = | | ||||||||||
0 | 0 | 0 | | 0 | | 0 | ||||||
| | | ||||||||||
0 | 0 | 0 | 0 | | 0 | | ||||||
| | 0 | ||||||||||
1 | 0 | 0 | 0 | 0 | 0 | 0 | ||||||
| | 0 | ||||||||||
0 | 1 | 0 | 0 | 0 | 0 | 0 | ||||||
Прибавим последние две строки матрицы  к первым двум по вышеуказанному правилу, получим
к первым двум по вышеуказанному правилу, получим | | | | | | | * | | | | | | |
1 | 0 | | 0 | | 0 | 0 | | | | (5) | |||
| | | |||||||||||
0 | 1 | 0 | | 0 | | 0 | |||||||
| | | |||||||||||
0 | 0 | | 0 | | 0 | | |||||||
| = | | |||||||||||
0 | 0 | 0 | | 0 | | 0 | |||||||
| | | |||||||||||
0 | 0 | 0 | 0 | | 0 | | |||||||
| | 0 | |||||||||||
1 | 0 | 0 | 0 | 0 | 0 | 0 | |||||||
| | 0 | |||||||||||
0 | 1 | 0 | 0 | 0 | 0 | 0 | |||||||
Отметим, что в модифицированной задаче (5) векторы ненулевых диагоналей имеют вид
 ,
,  ,
,  .
.На основе теоремы Кронекера – Капелли легко показать существование и единственность решения задачи (3) при условии существования и единственности решения задачи (1).
Необходимо отметить, что проведённая трансформация системы уравнений привела её матрицу коэффициентов к верхнетреугольному виду с нижним окаймлением. Это означает, что в прямом ходе метода Гаусса все подлежащие исключению ненулевые элементы матрицы (в том числе и вновь возникающие) располагаются только в её S последних строках.
3. Представление данных
В задаче (3), как правило, матрица ![]() является сильно разреженной, поэтому нецелесообразно хранить все элементы матрицы. Так уже при n = 10000 для хранения матрицы A, каждый элемент которой представлен числом с плавающей точкой двойной точности, требуется около 745 Мб.
является сильно разреженной, поэтому нецелесообразно хранить все элементы матрицы. Так уже при n = 10000 для хранения матрицы A, каждый элемент которой представлен числом с плавающей точкой двойной точности, требуется около 745 Мб.
Матрица ![]() полностью определяется следующими параметрами и векторами:
полностью определяется следующими параметрами и векторами:
· n – размерность одной строки матрицы A;
· S – смещение матрицы A;
· L– ширина ленты матрицы A;
· N – число ненулевых диагоналей матрицы A;
· ![]() – векторы размерностью n, содержащие элементы k-ой ненулевой диагонали матрицы A;
– векторы размерностью n, содержащие элементы k-ой ненулевой диагонали матрицы A;
· p– вектор размерности ![]() , где
, где ![]() равен номеру i-ой ненулевой диагонали, отсчитанному от d1.
равен номеру i-ой ненулевой диагонали, отсчитанному от d1.
Вектора cи xсохраняют свое представление, указанное в (2).
Для матрицы A` дополнительно введем векторы ![]() . Каждый из этих векторов имеет размерность Lи содержит отличные от 0 элементы строки матрицы A` с номером
. Каждый из этих векторов имеет размерность Lи содержит отличные от 0 элементы строки матрицы A` с номером ![]() .
.
При таком подходе к представлению данных система из 10000 уравнений с ![]() и
и ![]() занимает около 0,3 Мб. Без введения вектора p эта же задача занимала бы в памяти 7,62 Мб (нет возможности учесть диагонали, состоящие из нулей внутри ленты).
занимает около 0,3 Мб. Без введения вектора p эта же задача занимала бы в памяти 7,62 Мб (нет возможности учесть диагонали, состоящие из нулей внутри ленты).
4. Прямой ход алгоритма
Первоначально первые S уравнений задачи (3) вычитаются из последних S уравнений системы по следующему правилу: из уравнения с номером ![]() вычитается уравнение с номером
вычитается уравнение с номером ![]() . Для примера (4) получим систему
. Для примера (4) получим систему
| | | | | | | * | | | |
|
1 | 0 | | 0 | | 0 | 0 | | | | ||
0 | 1 | 0 | | 0 | | 0 | | | | ||
0 | 0 | | 0 | | 0 | | | | | ||
0 | 0 | 0 | | 0 | | 0 | | = | | ||
0 | 0 | 0 | 0 | | 0 | | | | | ||
0 | 0 | | 0 | | 0 | 0 | | | | ||
0 | 0 | 0 | | 0 | | 0 | | | | ||
Тогда векторы ![]() принимают вид
принимают вид ![]() ,
, ![]() .
.
Далее начинается итерационный процесс, состоящий из ![]() итераций. Каждая итерация состоит из двух шагов. На первом шаге компоненты векторов
итераций. Каждая итерация состоит из двух шагов. На первом шаге компоненты векторов ![]() и c` вычисляются по формулам
и c` вычисляются по формулам
![]() ,
,
![]() ,
,
 ,
,
![]() . (6)
. (6)
В выражении (6) индекс i- номер итерации, ![]() - номер ненулевой диагонали в векторе
- номер ненулевой диагонали в векторе ![]() , стоящий на позиции m,
, стоящий на позиции m, ![]() – значение j-го компонента вектора
– значение j-го компонента вектора ![]() на итерации с номером i,
на итерации с номером i, ![]() – значение компоненты вектора c` с индексом
– значение компоненты вектора c` с индексом ![]() на итерации с номером i.
на итерации с номером i.
На втором шаге итерации выполняется циклический сдвиг векторов ![]() на один элемент влево.
на один элемент влево.
Из выражения (6) легко видеть возможность независимого вычисления компонентов векторов ![]() , что позволяет параллельно производить вычисления в общем случае на
, что позволяет параллельно производить вычисления в общем случае на ![]() независимых узлах вычислительной системы.
независимых узлах вычислительной системы.
После выполнения ![]() итераций в правом нижнем углу матрицы коэффициентов образуется (возможно, полностью заполненная) подматрица Q размерности SxS. Для примера (4) получаем
итераций в правом нижнем углу матрицы коэффициентов образуется (возможно, полностью заполненная) подматрица Q размерности SxS. Для примера (4) получаем
| | | | | | | * | | | |
| |
1 | 0 | | 0 | | 0 | 0 | | | | |||
| | | ||||||||||
0 | 1 | 0 | | 0 | | 0 | ||||||
| | | ||||||||||
0 | 0 | | 0 | | 0 | | ||||||
| = | | ||||||||||
0 | 0 | 0 | | 0 | | 0 | ||||||
| | | ||||||||||
0 | 0 | 0 | 0 | | 0 | | ||||||
| | | ||||||||||
0 | 0 | 0 | 0 | 0 | | | ||||||
| | | ||||||||||
0 | 0 | 0 | 0 | 0 | | | ||||||
При этом векторы ![]() имеют вид
имеют вид ![]() ,
, ![]() . В частном случае некоторые диагональные элементы
. В частном случае некоторые диагональные элементы ![]() могут быть равны нулю, что потребует переупорядочивания последних S строк матрицы A`.
могут быть равны нулю, что потребует переупорядочивания последних S строк матрицы A`.
Перед выполнением следующего этапа требуется синхронизировать работу программы. Для последних S уравнений задачи (3) выполняется прямой ход метода Гаусса. Для примера (4) имеем
| | | | | | | * | | | |
| |
1 | 0 | | 0 | | 0 | 0 | | | | |||
| | | ||||||||||
0 | 1 | 0 | | 0 | | 0 | ||||||
| | | ||||||||||
0 | 0 | | 0 | | 0 | | ||||||
| = | | ||||||||||
0 | 0 | 0 | | 0 | | 0 | ||||||
| | | ||||||||||
0 | 0 | 0 | 0 | | 0 | | ||||||
| | | ||||||||||
0 | 0 | 0 | 0 | 0 | | | ||||||
| | | ||||||||||
0 | 0 | 0 | 0 | 0 | | | ||||||
Тогда вектора ![]() примут вид
примут вид ![]() ,
, ![]() .
.
5. Обратный ход алгоритма
Обратный ход алгоритма полностью совпадает с аналогичным этапом канонического метода Гаусса.
6. Схема метода для многопроцессорной вычислительной системы
Рассматриваем вычислительную систему с общей памятью, включающую p процессоров. Схема метода решения задачи на вычислительной системе данной архитектуры выглядит следующим образом.
1) Какой-либо из процессоров назначается главным (master-процессор), а все остальные - вспомогательными (slave-процессоры). На master-процессоре запускается основной процесс алгоритма.
2) В оперативную память системы загружаются исходные данные решаемой задачи.
3) На master–процессоре выполняем модификацию задачи (1) согласно изложенному выше алгоритму.
4) Запускается ![]() потоков управления, каждому из которых передаётся на обработку z=
потоков управления, каждому из которых передаётся на обработку z=![]() векторов
векторов ![]() . Если S не кратно p, то последний поток управления получит меньше векторов
. Если S не кратно p, то последний поток управления получит меньше векторов ![]() чем остальные. Распределение потоков управления по процессорам выполняется планировщиком операционной системы. При обработке данных участвуют как master-процессор, так и slave-процессоры.
чем остальные. Распределение потоков управления по процессорам выполняется планировщиком операционной системы. При обработке данных участвуют как master-процессор, так и slave-процессоры.
5) Каждый поток управления, используя (6), производит модификацию векторов![]()
![]() где
где ![]() – номер потока управления.
– номер потока управления.
6) На master-процессоре выполняется прямой ход стандартного метода Гаусса для последних S уравнений модифицированной задачи.
7) На master-процессоре выполняется обратный ход метода Гаусса.
7. Аналитическая оценка эффективности алгоритма
Для начала оценим время выполнения итерации алгоритма на одном процессоре. На каждой итерации требуется выполнить не более чем S операций деления, ![]() операции умножения и
операции умножения и ![]() операций вычитания.
операций вычитания.
Пусть среднее время выполнения одной операции деления над числами с плавающей точкой двойной точности задаётся константой ![]() , а время выполнения прочих арифметических операций - константой
, а время выполнения прочих арифметических операций - константой ![]() . Тогда аналитическое выражение для времени выполнения прямого хода для всей системы имеет вид
. Тогда аналитическое выражение для времени выполнения прямого хода для всей системы имеет вид
![]() , (7)
, (7)
где ![]() – слагаемое, введенное для учета верхней границы числа арифметических операций, требуемых для решения СЛАУ из Sуравнений в конце выполнения прямого хода алгоритма. Константы
– слагаемое, введенное для учета верхней границы числа арифметических операций, требуемых для решения СЛАУ из Sуравнений в конце выполнения прямого хода алгоритма. Константы ![]() определяются экспериментально.
определяются экспериментально.
Оценим время выполнения данного алгоритма на многопроцессорной системе с общей оперативной памятью, используя рассмотренную выше схему метода:
![]() . (8)
. (8)
В (8) время ![]() - накладные расходы на модификацию задачи (1), запуск
- накладные расходы на модификацию задачи (1), запуск ![]() потоков и распределения их по процессорам,
потоков и распределения их по процессорам, ![]() – время выполнения вычислительных операций всеми процессорами:
– время выполнения вычислительных операций всеми процессорами:
![]() . (9)
. (9)
В формуле (9) величина ![]() – время решения части задачи i-ым процессором. В данную величину следует включить время обращения процессора к общей оперативной памяти. В случае, если все процессоры системы имеют одинаковую производительность и не имеют дополнительной вычислительно нагрузки, выражение (8) принимает вид
– время решения части задачи i-ым процессором. В данную величину следует включить время обращения процессора к общей оперативной памяти. В случае, если все процессоры системы имеют одинаковую производительность и не имеют дополнительной вычислительно нагрузки, выражение (8) принимает вид
![]() (10)
(10)
Отсюда получаем выражение для ускорения вычислительного процесса
![]() . (11)
. (11)
Ниже приведены результаты аналитического исследования алгоритма.
Пример 1. Отобразим зависимость ![]() для матрицы с n = 25000000, N = 5, S = 2500. Количество вспомогательных векторов
для матрицы с n = 25000000, N = 5, S = 2500. Количество вспомогательных векторов ![]() при модификации задачи составляет 2500, объем требуемой памяти - 1,02 Гб. Организационное время на создание одного потока принимается постоянным и составляет 0,0003 сек,
при модификации задачи составляет 2500, объем требуемой памяти - 1,02 Гб. Организационное время на создание одного потока принимается постоянным и составляет 0,0003 сек, ![]() Полученная зависимость приведена на рисунке 1.
Полученная зависимость приведена на рисунке 1.
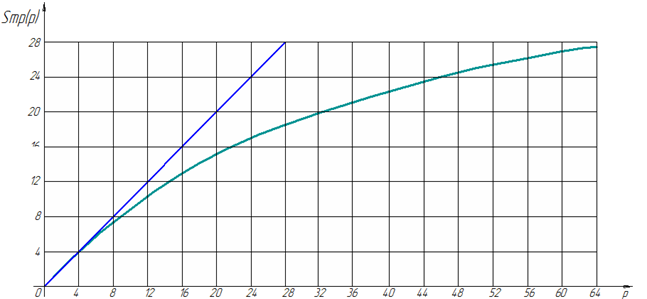
Рисунок 1. Зависимость ![]() от числа процессоров p для примера 1
от числа процессоров p для примера 1
На рисунке 2 дан график зависимости ускорения от смещения S ленты матрицы коэффициентов при фиксированном количестве процессов p=8.

Рисунок 2. Зависимость ![]() от смещения для примера 1
от смещения для примера 1
Пример 2. Здесь приводятся зависимости ускорения ![]() при
при ![]() и
и ![]() для задачи с n = 100000000, N = 10000, остальные исходные данные аналогичны примеру 1. Ниже на рисунках 3 и 4 приведены зависимости аналогичные зависимостям на рисунках 1 и 2.
для задачи с n = 100000000, N = 10000, остальные исходные данные аналогичны примеру 1. Ниже на рисунках 3 и 4 приведены зависимости аналогичные зависимостям на рисунках 1 и 2.

Рисунок 3. Зависимость ![]() от числа процессоров P для примера 2
от числа процессоров P для примера 2
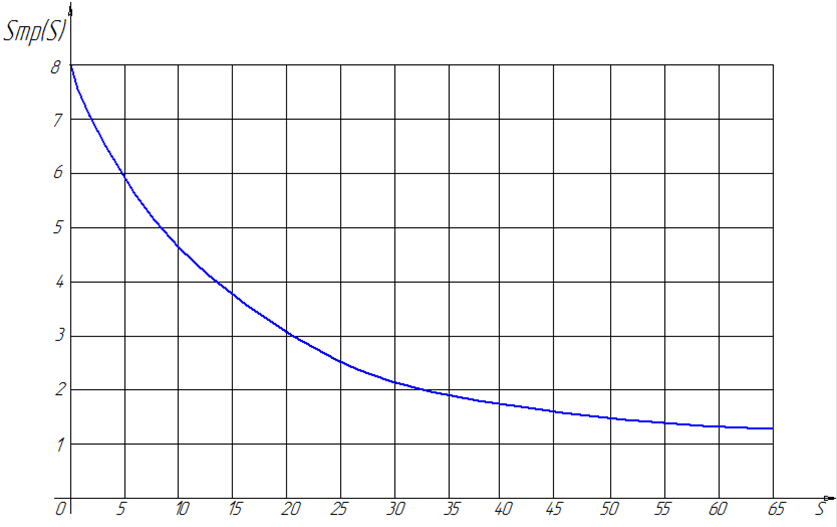
Рисунок 4. Зависимость ![]() от смещения для примера 2
от смещения для примера 2
Пример 3. Здесь даны зависимости ускорения ![]() при
при ![]() и
и ![]() для матрицы
для матрицы ![]() . Ниже на рисунках 5 и 6 приведены зависимости аналогичные зависимостям на рисунках 1 и 2.
. Ниже на рисунках 5 и 6 приведены зависимости аналогичные зависимостям на рисунках 1 и 2.

Рисунок 5. Зависимость ![]() от числа процессоров p для примера 3
от числа процессоров p для примера 3

Рисунок 6. Зависимость ![]() от смещения для примера 2
от смещения для примера 2
Пример 4. Здесь исследуется зависимость ускорения ![]() для задачи небольшой размерности
для задачи небольшой размерности ![]() , результат представлен на рисунке 7.
, результат представлен на рисунке 7.
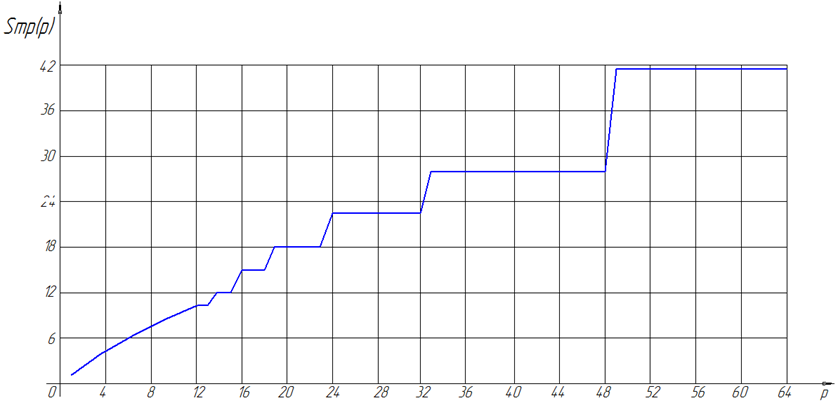
Рисунок 7. Зависимость ![]() от числа процессоров p для примера 4
от числа процессоров p для примера 4
Из рассмотренных выше примеров очевидно, что ускорение слабо зависит от размерности задачи, а зависит лишь от смещения. Ступеньки на рисунках 1, 3, 5, 7 появились из-за несбалансированности загрузки системы, полученной в результате некратности чисел S и p. Так при увеличении p не всегда стоит ожидать кратного увеличения ускорения. Из рисунков 2, 4, 6 видно, как с ростом смещения падает ускорение, это связано с преобладанием слагаемого ![]() в (9). Наибольшая эффективность алгоритма достигается при равенстве количества процессоров системы p и смещения S.
в (9). Наибольшая эффективность алгоритма достигается при равенстве количества процессоров системы p и смещения S.
8. Программная реализация
Алгоритм реализован на языке высокого уровня C++ [8] с использованием стандартных библиотек многопоточного программирования операционной системы UNIX [9].
Ниже приведены результаты численных экспериментов для некоторых СЛАУ.
n = 100000, S = 400, N = 5.
Кол-во ядер | 1 | 2 | 3 | 4 |
| 8,12 | 4,42 | 3,03 | 2,09 |
| 1,00 | 1,83 | 2,67 | 3.87 |
n = 100000, S = 700, N =5.
Кол-во ядер | 1 | 2 | 3 | 4 |
| 31,40 | 16,22 | 11,17 | 8,19 |
| 1,00 | 1,93 | 2,81 | 3,83 |
n = 3000000, S = 400, N = 5.
Кол-во ядер | 1 | 2 | 3 | 4 |
| 243 | 127 | 86 | 64 |
| 1,00 | 1,910 | 2,820 | 3,790 |
n = 3000000, S = 700, N = 5.
Кол-во ядер | 1 | 2 | 3 | 4 |
| 957 | 492 | 322 | 254 |
| 1,00 | 1,94 | 2,97 | 3,76 |
Далее для n = 3000000, N = 5 приведена зависимость ускорения ![]() от S при использовании четырёхядерной вычислительной системы.
от S при использовании четырёхядерной вычислительной системы.
S | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 |
| 0,001 | 0,095 | 3,15 | 7,39 | 75,11 | 93 | 1192 | 11260 |
| 0,0037 | 0,254 | 11,28 | 26,17 | 266,93 | 328 | 2250 | 18353 |
| 3,70 | 3,58 | 3,58 | 3,55 | 3,55 | 3,52 | 1,88 | 1,63 |
Данные результаты полностью согласуются с аналитической оценкой эффективности алгоритма. Так с ростом ширины ленты эффективность алгоритма падает, а при одинаковой ширине ленты ускорение практически не зависит от размерности исходной задачи n.
Заключение
В статье предложен новый параллельный алгоритм решения систем линейных алгебраических уравнений с диагонально-ленточной матрицей коэффициентов, учитывающий наличие нулевых элементов в отдельных диагоналях внутри ленты.
Основными достоинствами алгоритма являются следующие.
- Простота программной реализации.
- Высокие показатели ускорения для задач с малым смещением ленты матрицы коэффициентов.
- Экономия памяти вычислительной системы.
- Возможность простой адаптации под различные вычислительные системы с общей памятью.
- Отсутствие множественного доступа по записи к исходным данным.
К недостаткам алгоритма относятся следующие.
- Падение ускорения с увеличением смещения S ленты матрицы A.
- Необходимость выделения дополнительной памяти на этапе модификации исходной задачи.
- Возможная несбалансированность нагрузки процессоров вычислительной системы.
Список литературы
1. Ильин В.А., Позняк Э.Г. Линейная алгебра. М.: Физматлит, 1999. 280 с.
2. Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия. М.: Проспект, 2007. 400 с.
3. Ортега Дж. Введение в параллельные и векторные методы решения линейных систем: пер. с англ. М.: Мир, 1991. 367 с. [Ortega J.M. Introduction to Parallel and Vector Solution of Linear Systems. NY.: Plenum Press, 1988. 305 p.]
4. Tewarson R.P. Solution of linear equations with coefficient matrix in band form // BIT Numerical Mathematics. 1968. Vol. 8, iss. 1. P. 53-58. DOI: 10.1007/BF01939979
5. Saad Y., Schultz H. Parallel direct methods for solving banded linear systems // Linear Algebra Appl. 1987. Vol. 88-89. P. 623-650. http://dx.doi.org/10.1016/0024-3795(87)90128-5
6. Polizzi E., Sameh A. SPIKE: A parallel environment for solving banded linear systems // Computers & Fluids. 2007. Vol. 36, no. 1. P. 113-141. http://dx.doi.org/10.1016/j.compfluid.2005.07.005
7. Krüger J., Westermann R. GPU Gems 2. Chapter 44. A GPU Framework for Solving Systems of Linear Equations. Режим доступа: http://http.developer.nvidia.com/GPUGems2/gpugems2_chapter44.html (дата обращения 19.06.2013).
8. Эккель Б. Философия C++. Введение в стандартный C++. СПб.: Питер, 2004. 572 с. [Eckel B. Thinking in C++: Introduction to Standard C++. NY.: PrenticeHall, 2000. 814 p.]
9. Чан Т. Системное программирование на C++ для Unix. М.: BHV, 1997. 490 с. [Chan T. UNIX System Programming using C++. Prentice Hall, 1997. 598 p.]
Публикации с ключевыми словами: параллельный алгоритм, система линейных алгебраических уравнений, многодиагональная матрица коэффициентов, многоленточная матрица коэффициентов, многопроцессорная вычислительная система
Публикации со словами: параллельный алгоритм, система линейных алгебраических уравнений, многодиагональная матрица коэффициентов, многоленточная матрица коэффициентов, многопроцессорная вычислительная система
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



