научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 08, август 2013
DOI: 10.7463/0813.0589299
УДК 621.9
Россия, МГТУ им. Н.Э. Баумана
Введение
Математические модели в резании металлов можно классифицировать как теоретические и экспериментальные (эмпирические) зависимости. Теоретические зависимости, представленные в работах Зорева, Розенберга, Клушина и других ученых, опираются на схему стружкообразования и включают в себя механические, технологические и физические свойства материала. Достоинством такого подхода является его универсальность, недостатком – затруднения при определении на практике требуемых характеристик. Экспериментальные зависимости, широко представленные в справочной литературе, являются эмпирическими моделями, полученными в результате математической обработки экспериментальных данных. Наиболее распространены степенные зависимости с корректирующими коэффициентами, которые получались на основе линейной аппроксимации при обработке данных в логарифмических координатах. А также модели, являющиеся произведением площади срезаемого слоя на дополнительные коэффициенты. Оба типа указанных зависимостей получены на основании серий однофакторных экспериментов и должны сопровождаться таблицами коэффициентов. Их достоинствами являются доступные для варьирования на практике параметры зависимости, простота получения и использования. Недостатками – оценочный характер, отсутствие учета совместного влияния параметров зависимости на результирующее значение, большое количество опытов и правомерность только в области проведенных экспериментов.
Самостоятельным направлением в математическом описании процессов механической обработки являются полиномиальные модели, полученные в результате спланированных многофакторных экспериментов. Такие зависимости, проходя через экспериментальные точки, с высокой степенью достоверности описывают все пространство эксперимента за счет возможности учета совместного влияния параметров на результат. Но полиномиальные модели требуют подготовки и планирования эксперимента, а также обработки и анализа их на базе специального математического аппарата.
Целью данной работы является формирование принципиального алгоритма получения и анализа многомерных полиномиальных зависимостей в резании металлов на примере токарной обработки и сравнение экспериментально полученных результатов с результатами математического анализа.
Научная новизна работы заключается в подтверждении положений, экспериментально полученных в [1]. В частности, математически доказано, что для минимизации энергозатрат на токарной обработке со снятием припуска за два прохода максимально возможный припуск должен сниматься на черновом проходе, обработка должна вестись на максимально возможных скоростях резания и подачах на оборот, причем подача на черновой обработке должна превышать подачу на чистовой.
Для достижения представленной цели и получения научных результатов поставлены и решены следующие задачи:
- экспериментально или на основе литературных источников определить факторы, наиболее сильно влияющие на динамические характеристики токарной обработки, и характер этого влияния;
- составить план эксперимента для получения полиномиальной модели тангенциальной составляющей силы резания и использования ее для модели энергопотребления при точении;
- оптимизировать параметры токарной обработки по критерию минимального суммарного энергопотребления черновой и чистовой обработки на базе специального математического аппарата.
1. Определение факторов эксперимента
При планировании эксперимента фактором называется независимая переменная величина, влияющая на параметр оптимизации. Каждый фактор имеет область определения, т.е. совокупность всех значений, которые он может принимать. Факторы должны быть управляемыми, т.е. позволяющими экспериментатору установить их требуемые значения и поддерживать постоянными эти значения в течение опыта, непосредственно воздействующими на объект исследования, совместимыми и независимыми друг от друга [2].
Особенностью планирования эксперимента с механической обработкой металлов являются технологические мероприятия, позволяющие сохранить условия обработки в процессе эксперимента близкими к постоянным. Например, для достоверности полученных результатов при исследованиях динамических характеристик при точении необходимо предельно сократить время непосредственного участия режущего лезвия в процессе обработки, чтобы величина износа, установленная в плане эксперимента, была близка к постоянной; вести обработку в области с минимальным отжатием заготовки, вызывающем вибрации и изменение глубины резания; проводить замеры составляющих силы резания на одном диаметре заготовки, чтобы сохранить идентичные условия в зоне резания и т.д. Перечисленные требования определяют необходимость предельно возможного сокращения количества опытов и их продолжительности для определения составляющих силы резания.
Одним из направлений указанного сокращения опытов является планирование дробного факторного эксперимента, подробно рассмотренного в работе [3] для токарной обработки. Но исследования по такой схеме показали, что достоверность результирующей полиномиальной функции во многом зависит от выбранной схемы смешивания оценок и установки на ее основе номеров кодов факторов при смешанном коэффициенте. Неточности и погрешности на этом этапе моделирования дробного факторного эксперимента приводят к неадекватности результирующей модели.
Другим направлением сокращения опытов является углубленный анализ параметров обработки, вводимых в качестве факторов в полном факторном эксперименте. В частности, по литературным источникам было установлено, что на силу резания при точении оказывают влияние параметры режима обработки (глубина резания t, мм; подача на оборот Sо, мм/об; скорость резания v, м/мин), параметры режущего инструмента (передний угол γ, град; главный угол в плане φ, град; величина износа режущей кромки по задней поверхности hз, мм) и твердость материала HB. При этом значение главного угла в плане φ в первую очередь оказывает влияние на перераспределение долей осевой и радиальной составляющих силы резания [4], влияние на тангенциальную составляющую, которая определяет мощность резания и энергопотребление, не превышает 10%; кроме того, значение угла φ часто определено конструктивными особенностями детали и не может подвергаться варьированию. В свою очередь возможность управления передним углом γ при использовании сменных многогранных пластин исключена из-за наличия сложного рельефа передней поверхности.
Экспериментальные исследования, подготовленные и проведенные для анализа влияния глубины и скорости резания, подачи на оборот и износа по задней поверхности, как потенциальных факторов полиномиальной зависимости, дали результаты, представленные ниже и проиллюстрированы рисунками 1 ... 5. Во всех случаях рассмотрена токарная обработка стали 45 ГОСТ 1050-74 резцами из твердого сплава Т15К6 ГОСТ 3882-74.
На рисунке 1 представлены экспериментальные зависимости тангенциальной составляющей силы резания от глубины резания при различных подачах на оборот. Общую зависимость можно характеризовать как монотонно возрастающую, близкую к линейной. При изменении глубины резания 0,5 мм до 3,5 мм величина силы резания возрастает более чем в 3...5 раз.

Рисунок 1. Зависимость тангенциальной составляющей силы резания от глубины резания при различных подачах на оборот (v = 91 м/мин, HB 200, γ = 10°, φ = 45°, hз = 0).
Влияние подачи на тангенциальную составляющую силы резания при различных скоростях резания представлено на рисунке 2. Аналогично предыдущей зависимость характеризуется как монотонно возрастающая, близкая к линейной. При изменении подачи от 0,07 мм/об до 0,39 мм/об величина тангенциальной составляющей силы резания возрастает более чем в 3...4 раза.

Рисунок 2. Зависимость тангенциальной составляющей силы резания от подачи при различных скоростях резания (t = 2 мм, HB 200, γ = 10°, φ = 45°, hз = 0).
Зависимость силы резания от скорости резания не является монотонной в диапазоне технологически допустимых значений аргумента (рисунок 3). Кривая имеет экстремумы, положение которых определяется сочетанием обрабатываемого и инструментального материалов и другими параметрами обработки.
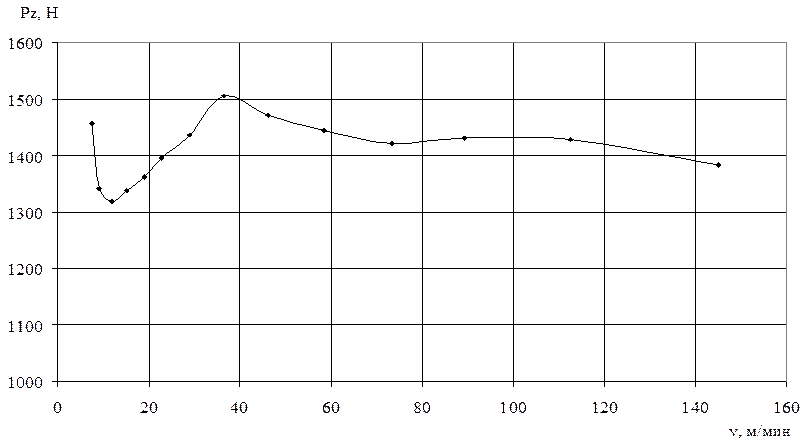
Рисунок 3. Зависимость тангенциальной составляющей силы резания от скорости резания (t = 2 мм, So = 0,3 мм/об, HB 200, γ = 10°, φ = 45°, hз = 0).
Влияние износа по задней поверхности получено с помощью однофакторных экспериментов при различных параметрах режима обработки. Замеры проводились при эксплуатации треугольных СМП, работавших в одинаковых производственных условиях, текущий износ которых составил соответственно 0; 0,146; 0,235; 0,35 и 0,581 мм (рисунок 4). Результаты экспериментов представлены на рисунке 5.

Рисунок 4. Вид задней поверхности экспериментальных изношенных пластинок.
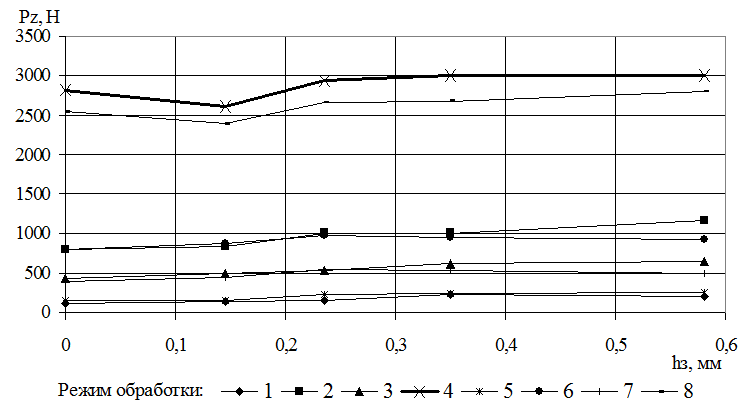
Рисунок 5. Графики зависимости тангенциальной составляющей силы резания от износа по задней поверхности при различных режимах обработки:
Номер режима обработки: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Глубина резания t, мм: | 0,5 | 3 | 0,5 | 3 | 0,5 | 3 | 0,5 | 3 |
Подача на оборот Sо, мм/об: | 0,097 | 0,097 | 0,39 | 0,39 | 0,097 | 0,097 | 0,39 | 0,39 |
Скорость резания v, м/мин: | 56 | 56 | 56 | 56 | 139 | 139 | 139 | 139 |
Во всех сериях эксперимента, согласно графикам, с увеличением износа изменяется сила резания, суммарное увеличение которой составляет от 15% на режиме 4 до 78% на режиме 5. На графиках видно, что при небольшой величине износа может наблюдаться уменьшение силы резания, а затем ее монотонное увеличение на всех рассмотренных режимах обработки.
Экспериментальные исследования твердости поковок позволили принять, что твердость заготовок в партии из одной плавки является одинаковой с некоторыми отклонениями от математического ожидания.
В результате глубина резания t, подача на оборот Sо, скорость резания v и величина износа режущей кромки по задней поверхности hз удовлетворяют всем требованиям к факторам полного факторного эксперимента, причем при назначении уровней двух последних следует учесть нелинейный характер их влияния на объект исследования.
2. Составление плана эксперимента
Число опытов N в полном факторном эксперименте определяется числом всех сочетаний уровней факторов, т.е. N = mn, где m – число уровней каждого фактора, n – число факторов. Таким образом, при n = 4 минимальное число опытов на двух уровнях составляет 16, а на трех уровнях 81. Поскольку увеличение числа опытов может привести к изменениям условий эксперимента с течением времени, желательно ограничиться двумя уровнями его варьирования, если нет априори известной экстремальной зависимости результата от какого-либо исследуемого фактора. В рассматриваемом примере получения полиномиальной зависимости тангенциальной составляющей силы резания при точении уровни подачи и глубины резания могут быть назначены на всем технологически допустимом диапазоне варьирования. При назначении уровней износа и скорости резания должны быть учтены участки монотонности: для скорости нижний уровень должен превышать 50 м/мин; для износа верхний уровень либо не должен превышать 0,2 мм (что соответствует рекомендациям многих производителей), либо сравнивать новый инструмент со значительно изношенным до 0,6...0,8 мм, линеаризируя экспериментальные кривые.
Математическая обработка результатов может осуществляться при равномерном дублировании опытов, при неравномерном дублировании и при отсутствии дублирования. В управляемом эксперименте желательно обеспечить равномерное дублирование.
Уровни варьируемых факторов для проведения экспериментальных исследований представлены в таблице 1, а матрица планирования эксперимента в таблице 2.
Таблица 1.
Значения уровней варьируемых факторов.
Уровни и интервалы | Факторы | |||||||
1 | 2 | 3 | 4 | |||||
натуральное значение | значение в кодах | натуральное значение | значение в кодах | натуральное значение | значение в кодах | натуральное значение | значение в кодах | |
глубина резания t, мм | лx1 | подача на оборот Sо, мм/об | x2 | скорость резания v, м/мин | x3 | величина износа по задней поверхности hз, мм | x4 | |
Уровень 1 | 1 | -1 | 0,1 | -1 | 86 | -1 | 0 | -1 |
Уровень 2 | 5 | +1 | 0,5 | +1 | 138 | +1 | 0,17 | +1 |
Основной уровень | 3 | - | 0,3 | - | 112 | - | 0,085 | - |
Интервал варьирования | 2 | - | 0,2 | - | 26 | - | 0,085 | - |
Значение в кодах получено по формуле [2]:
| (1) |
где ![]() - натуральное значение i-того фактора (например, t = 5 мм),
- натуральное значение i-того фактора (например, t = 5 мм), ![]() - натуральное значение основного уровня i-того фактора (t0 = 3 мм), εi – интервал варьирования i-того фактора (определяется от основного уровня, εt = 2 мм).
- натуральное значение основного уровня i-того фактора (t0 = 3 мм), εi – интервал варьирования i-того фактора (определяется от основного уровня, εt = 2 мм).
Представленная матрица сформирована для наиболее простой полиномиальной зависимости, в которой не включены степени выше первой для каждого фактора, но представлен весь спектр возможного совместного влияния факторов эксперимента. В общем виде уравнение выглядит следующим образом:
| (2) |
Таблица 2.
Матрица планирования полного факторного эксперимента 24.
№ | x0 | x1 | x2 | x3 | x4 | x1x2 | x1x3 | x1x4 | x2x3 | x2x4 | x3x4 | x1x2x3 | x1x2x4 | x1x3x4 | x2x3x4 | x1x2x3x4 | y |
1 | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | + | y1 |
2 | + | + | + | + | - | + | + | - | + | - | - | + | - | - | - | - | y2 |
3 | + | + | + | - | + | + | - | + | - | + | - | - | + | - | - | - | y3 |
4 | + | + | + | - | - | + | - | - | - | - | + | - | - | + | + | + | y4 |
5 | + | + | - | + | + | - | + | + | - | - | + | - | - | + | - | - | y5 |
6 | + | + | - | + | - | - | + | - | - | + | - | - | + | - | + | + | y6 |
7 | + | + | - | - | + | - | - | + | + | - | - | + | - | - | + | + | y7 |
8 | + | + | - | - | - | - | - | - | + | + | + | + | + | + | - | - | y8 |
9 | + | - | + | + | + | - | - | - | + | + | + | - | - | - | + | - | y9 |
10 | + | - | + | + | - | - | - | + | + | - | - | - | + | + | - | + | y10 |
11 | + | - | + | - | + | - | + | - | - | + | - | + | - | + | - | + | y11 |
12 | + | - | + | - | - | - | + | + | - | - | + | + | + | - | + | - | y12 |
13 | + | - | - | + | + | + | - | - | - | - | + | + | + | - | - | + | y13 |
14 | + | - | - | + | - | + | - | + | - | + | - | + | - | + | + | - | y14 |
15 | + | - | - | - | + | + | + | - | + | - | - | - | + | + | + | - | y15 |
16 | + | - | - | - | - | + | + | + | + | + | + | - | - | - | - | + | y16 |
3. Обработка результатов эксперимента
Опыты проведены на станке модели 16К20 сборным токарным резцом с пластиной Т15К6 без покрытия (α = 8°, γ = 12°, α' = 6°, φ = 45°) на прутке диаметром 88 мм из стали 45 ГОСТ 1050-74. Замеры тангенциальной составляющей силы резания Pz проведены на динамометрической установке, включающей динамометр УДМ600, тензометрический усилитель 8АНЧ-21 и компьютер с платой аналого-цифрового преобразователя (АЦП) LA70M4. Реализованный план полного факторного эксперимента с результатами опытов и статистической обработки представлен в таблице 3.
Для каждого опыта, т.е. строки в плане эксперимента, определены среднее значение тангенциальной составляющей силы резания Pz сред, дисперсия и среднее квадратическое отклонение. С помощью G-критерия Кохрена при 5%-ном уровне значимости принята гипотеза однородности дисперсий, на основании чего определены коэффициенты регрессии в уравнении (2). Все расчеты выполнены по рекомендациям [2]. Далее по критерию Стьюдента при 5%-ном уровне значимости выявлены незначащие коэффициенты: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . В результате получена следующая модель:
. В результате получена следующая модель:
| (3) |
На основании F-критерия Фишера для адекватности при 5%-ном уровне значимости принята гипотеза адекватности полученной модели (3).
После преобразований, обратных кодированию, по формуле (1) полиномиальная зависимость тангенциальной составляющей силы резания при точении в указанных ранее условиях выглядит следующим образом:
| (4) |
Таблица 3.
План полного факторного эксперимента с результатами опытов и статистической обработки.
№ | Глубина резания t, мм | Подача на оборот Sо, мм/об | Скорость резания v, м/мин | Величина износа по задней поверхности hз, мм | Среднее значение тангенциальной составляющей силы резания Pz сред, Н | Дисперсия, Н2 | Среднее квадрати-ческое отклонение, Н | G-критерий Кохрена | Табличное значение G-критерия Кохрена | F-критерий Фишера для адекватности | Табличное значение F-критерия Фишера для адекватности | |
01 | 5 | 0,5 | 138 | 0,17 | 2266 | 7581 | 87 | 0,307 | 0,322 | 0,69 | 2,4 | |
02 | 5 | 0,5 | 138 | 0,00 | 2258 | 4950 | 70 | |||||
03 | 5 | 0,5 | 86 | 0,17 | 2214 | 4734 | 69 | |||||
04 | 5 | 0,5 | 86 | 0,00 | 2305 | 36 | 6 | |||||
05 | 5 | 0,1 | 138 | 0,17 | 898 | 320 | 18 | |||||
06 | 5 | 0,1 | 138 | 0,00 | 677 | 712 | 27 | |||||
07 | 5 | 0,1 | 86 | 0,17 | 910 | 3670 | 61 | |||||
08 | 5 | 0,1 | 86 | 0,00 | 709 | 1556 | 39 | |||||
09 | 1 | 0,5 | 138 | 0,17 | 454 | 234 | 15 | |||||
10 | 1 | 0,5 | 138 | 0,00 | 411 | 519 | 23 | |||||
11 | 1 | 0,5 | 86 | 0,17 | 479 | 27 | 5 | |||||
12 | 1 | 0,5 | 86 | 0,00 | 520 | 56 | 7 | |||||
13 | 1 | 0,1 | 138 | 0,17 | 162 | 12 | 3 | |||||
14 | 1 | 0,1 | 138 | 0,00 | 140 | 149 | 12 | |||||
15 | 1 | 0,1 | 86 | 0,17 | 159 | 35 | 6 | |||||
16 | 1 | 0,1 | 86 | 0,00 | 165 | 104 | 10 |
Полученная полиномиальная зависимость с высокой точностью описывает и экспериментальные точки, и промежуточные точки пространства эксперимента. Но полином не дает возможности визуальной оценки влияния каждого из параметров обработки (факторов эксперимента) на результирующее значение, а определение минимального или максимального значения требует использования дополнительного математического аппарата. В частности, для определения экстремума полиномиальной зависимости (функции) необходимо решить систему уравнений, являющуюся совокупностью приравненных к нулю частных производных по всем аргументам (найти градиент функции и приравнять его к нулю). Но особенностью инженерных задач является то, что их математическое решение должно удовлетворять техническим и технологическим критериям, поэтому при решении на каждый из аргументов накладываются ограничения.
Поскольку на границе заданной области отсутствует полноценная d-окрестность, необходимая для математических понятий максимума и минимума функции, задача нахождения минимального значения функции с учетом заранее наложенных ограничений делится на два самостоятельных алгоритма: нахождение минимального значения на границе и внутри заданного пространства [6].
Поиск минимального значения на границе ограниченной функции может быть осуществлен по методу множителей Лагранжа – методу нахождения минимума функции ![]() относительно наложенных k ограничений, где каждая точка n-мерного пространства функции
относительно наложенных k ограничений, где каждая точка n-мерного пространства функции ![]() описывается вектором
описывается вектором ![]() , т.е.
, т.е. ![]() – с наложенным дополнительным условием Каруша-Куна-Такера.
– с наложенным дополнительным условием Каруша-Куна-Такера.
4. Решение задачи оптимизации параметров токарной обработки по критерию минимального суммарного энергопотребления черновой и чистовой обработки
В работе [1] было экспериментально установлено, что степень влияния соотношения припусков чернового и чистового проходов на тенденцию изменения суммарного энергопотребления зависит от соотношения подач при обработке. Решение на основе перечисленных выше математических методов не позволит наглядно отобразить какие-либо тенденции, но позволит решить оптимизационную задачу, рассматривая еще и факторы скорости резания и износа в многомерном пространстве эксперимента. Расчеты произведены для обработки диаметра 90 мм на длине 100 мм с припуском под два прохода 5 мм на сторону аналогично однофакторным экспериментальным исследованиям, представленным в [1].
Энергия E, затрачиваемая на один технологический проход при токарной обработке:
| (5) |
где ![]() – основное технологическое время, мин;
– основное технологическое время, мин; 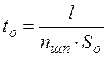 , l – длина обработки, мм, nшп – частота вращения шпинделя, об/мин.
, l – длина обработки, мм, nшп – частота вращения шпинделя, об/мин.
Принимая, что  , где d – диаметр заготовки, мм, имеем:
, где d – диаметр заготовки, мм, имеем:
| (6) |
где ![]() определено уравнением (4).
определено уравнением (4).
Суммарное энергопотребление двух технологических проходов записывается как:
| (7) |
где индексы 1 и 2 принадлежат параметрам чернового и чистового прохода соответственно; ![]() ,
, ![]() , учитывая, что припуск чистового прохода
, учитывая, что припуск чистового прохода ![]() .
.
Ограничения, для применения их в данном методе, должны быть представлены неравенствами вида![]() , где i – порядковый номер от 1 до k. Они представляют собой технические или технологические ограничения, определяющие область исследования. Причем ограничения, заданные двойными неравенствами, вырождаются в K = 2k ограничений, используемых в методе множителей Лагранжа. Ограничения, накладываемые на аргументы функции (7), определены экспериментальными исследованиями и рекомендациями из справочной литературы и сведены в таблицу 4.
, где i – порядковый номер от 1 до k. Они представляют собой технические или технологические ограничения, определяющие область исследования. Причем ограничения, заданные двойными неравенствами, вырождаются в K = 2k ограничений, используемых в методе множителей Лагранжа. Ограничения, накладываемые на аргументы функции (7), определены экспериментальными исследованиями и рекомендациями из справочной литературы и сведены в таблицу 4.
Таблица 4.
Ограничения на аргументы функции (7).
| Параметр обработки | Нижняя граница включительно | Верхняя граница включительно | ||||
значение | ограничение в общем виде | ограничение на границе | значение | ограничение в общем виде | ограничение на границе | ||
Черновой проход |
| 3,5 |
|
| 4,0 |
|
|
| 0,02 |
|
| 0,4 |
|
| |
| 80 |
|
| 140 |
|
| |
| 0 |
|
| 0,2 |
|
| |
Чистовой проход |
| 0,01 |
|
| 0,05 |
|
|
| 80 |
|
| 140 |
|
| |
| 0 |
|
| 0,2 |
|
| |
Функция (7) удовлетворяет всем требуемым условиям для использования метода множителей Лагранжа: на нее наложены ограничения, она дифференцируемая и гладкая на всей области исследования. Функция Лагранжа примет следующий вид:
| (8) |
где ![]() - исследуемая функция,
- исследуемая функция, ![]() - множители Лагранжа.
- множители Лагранжа.
Дополнительное условие Каруша-Куна-Такера:
| (9) |
где точка ![]() - точка минимума, а условия
- точка минимума, а условия ![]() представлены в таблице 4.
представлены в таблице 4.
Для определения экстремумов функции внутри области исследования найдем ее градиент и приравняем его к нулю:
| (10) |
Точка экстремума является точкой минимума функции, если ее матрица Гессе - матрица вторых частных производных, описывающая поведение функции во втором порядке - положительно определенная.
Решение систем (9) и (10) с предположением, что все ограничения активы, т.е. ![]() , и с проверкой матрицы Гессе произведено с помощью программного пакета MatLab. Результат решения представлен в таблице 5.
, и с проверкой матрицы Гессе произведено с помощью программного пакета MatLab. Результат решения представлен в таблице 5.
Таблица 5.
Координаты минимальных точек на границе и внутри области исследования функции (7).
Параметр обработки |
мм |
мм/об |
м/мин |
мм |
мм/об |
м/мин |
мм | Eсум, Дж |
Значение | 4,0 | 0,4 | 140 | 0 | 0,05 | 140 | 0 | 165675 |
В результате расчетов установлено, что при указанных выше условиях на токарной обработке снятие припуска за два прохода требует минимальных затрат электроэнергии при параметрах обработки, лежащих на границе исследуемой области. Аналитический расчет подтвердил тенденции, экспериментально полученные в [1]: максимально возможный припуск должен сниматься на черновом проходе, обработка должна вестись на максимально возможных скоростях резания и подачах на оборот, причем подача на черновой обработке должна превышать подачу на чистовой. Расчетная величина затрачиваемой энергии в исследуемой области составляет 165675 Дж или 0,046 кВт×ч.
Выводы.
1. В результате анализа характера влияния параметров обработки на тангенциальную составляющую силы резания при точении с целью введения их в качестве факторов в полный факторный эксперимент получено, что глубина резания t, подача на оборот Sо, скорость резания v и величина износа режущей кромки по задней поверхности hз удовлетворяют всем требованиям к факторам полного факторного эксперимента, причем при назначении уровней двух последних следует учесть нелинейный характер их влияния на объект исследования. В полученной экспериментальной зависимости отражены линейные эффекты и эффекты совместного влияния параметров обработки на результат.
2. Математическое исследование полиномиальных многомерных зависимостей с наложенными технологическими ограничениями требует математического аппарата, обеспечивающего решение двух самостоятельных задач: нахождение минимального значения на границе и внутри заданного пространства. Для чего может быть использован метод множителей Лагранжа с наложенным дополнительным условием Каруша-Куна-Такера и проверка матрицы Гессе экстремальных точек внутри пространства.
3. В результате расчетов подтверждены тенденции, экспериментально полученные в [1]. В частности, для минимизации энергозатрат на токарной обработке со снятием припуска за два прохода максимально возможный припуск должен сниматься на черновом проходе, обработка должна вестись на максимально возможных скоростях резания и подачах на оборот, причем подача на черновой обработке должна превышать подачу на чистовой.
Список литературы
1. Малькова Л.Д. Энергосбережение при проектировании технологической операции токарной обработки // Известия ВУЗов. Машиностроение. 2011. Спец. выпуск. С. 43-49.
2. Спиридонов А.А. Планирование эксперимента при исследовании технологических процессов. М.: Машиностроение, 1981. 184 с.
3. Древаль А.Е., Малькова Л.Д. Совместное влияние параметров механической обработки на величину составляющих силы резания // Известия ВУЗов. Машиностроение. 2007. № 8. С. 53-61.
4. Грановский Г.И., Грановский В.Г. Резание металлов: учебник для машиностроительных и приборостроительных специальностей вузов. М.: Высшая школа, 1985. 304 с.
5. Львовский Е.Н. Статистические методы построения эмпирических формул: учеб. пособие для втузов. 2-е изд., перераб. и доп. М.: Высшая школа, 1988. 239 с.
6. Зорич В.А. Математический анализ. Часть 1. 2-е изд., испр. и доп. М.: ФАЗИС, 1997. 554 с.
Публикации с ключевыми словами: сила резания, токарная обработка, энергопотребление, полиномиальная модель, полный факторный эксперимент
Публикации со словами: сила резания, токарная обработка, энергопотребление, полиномиальная модель, полный факторный эксперимент
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||
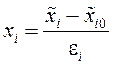 ,
,
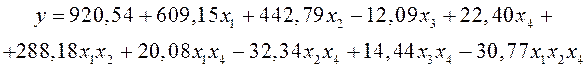
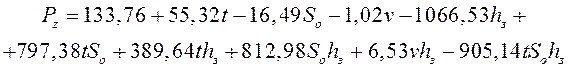
 , кВт
, кВт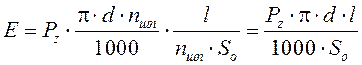 , Дж
, Дж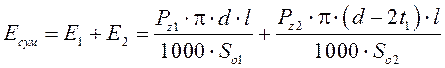 , Дж
, Дж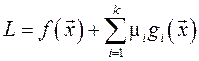
 ,
,


