научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 07, июль 2013
DOI: 10.7463/0713.0588392
УДК: 53.083
Россия, Волгоградский Государственный Университет
Введение
Измерение разности фаз является важной задачей радиотехники и радиофизики. Прецизионные фазометры используются в радиодальномерах и измерителях геометрических параметров объектов [1]. При этом для достижения с помощью стандартных измерителей погрешности фазовых измерений ![]() необходимо обеспечить отношение сигнал/шум порядка 120 дБ, что нереально для радиоволновых измерений. Высокоскоростные цифровые системы получения и обработки данных позволяют заменить устаревшие аналоговые и цифровые методы измерения разности фаз [2] на более совершенные, использующие априорную информацию о математической модели сигнала [3]. Реализация фазометра в виде аппаратно-программной системы реального времени [4] при ограниченных вычислительных возможностях цифровой системы обработки данных возможна на основе параметрических методов, позволяющих с минимальными вычислительными и временными затратами получить оценку измеряемых параметров сигнала.
необходимо обеспечить отношение сигнал/шум порядка 120 дБ, что нереально для радиоволновых измерений. Высокоскоростные цифровые системы получения и обработки данных позволяют заменить устаревшие аналоговые и цифровые методы измерения разности фаз [2] на более совершенные, использующие априорную информацию о математической модели сигнала [3]. Реализация фазометра в виде аппаратно-программной системы реального времени [4] при ограниченных вычислительных возможностях цифровой системы обработки данных возможна на основе параметрических методов, позволяющих с минимальными вычислительными и временными затратами получить оценку измеряемых параметров сигнала.
Существующие методы цифровой фазометрии в качестве априорной информации используют модель гармонического сигнала с постоянной амплитудой и мгновенной частотой [5], однако в реальных радиоволновых измерениях более адекватной является модель квазигармонического сигнала
![]() , (1)
, (1)
где a(t) – огибающая, ![]() – мгновенная частота [6]. Серьезным препятствием непосредственного применения известных методов фазовых измерений [2, 5] к квазигармоническим сигналам вида (1) является неоднозначность определения полной фазы сигнала θ(t) при наличии амплитудной модуляции a(t) [7]. В радиотехнике это явление известно как амплитудно-фазовая конверсия. Действительно, соотношение (1) ставит в соответствие одной функции x(t) два переменных параметра a(t) и θ(t), однозначное определение которых требует дополнительного условия. В работе [8] показано, что при медленном изменении частоты, параметры a(t) и θ(t) могут быть восстановлены однозначно. Эксперименты, проведенные с электромеханической установкой [9], показали, что при отношении сигнал/шум для наблюдаемого сигнала 50 дБ и значительной амплитудной и частотной модуляции возможно восстановление полной фазы квазигармонического сигнала с погрешностью не хуже 10–6 рад.
– мгновенная частота [6]. Серьезным препятствием непосредственного применения известных методов фазовых измерений [2, 5] к квазигармоническим сигналам вида (1) является неоднозначность определения полной фазы сигнала θ(t) при наличии амплитудной модуляции a(t) [7]. В радиотехнике это явление известно как амплитудно-фазовая конверсия. Действительно, соотношение (1) ставит в соответствие одной функции x(t) два переменных параметра a(t) и θ(t), однозначное определение которых требует дополнительного условия. В работе [8] показано, что при медленном изменении частоты, параметры a(t) и θ(t) могут быть восстановлены однозначно. Эксперименты, проведенные с электромеханической установкой [9], показали, что при отношении сигнал/шум для наблюдаемого сигнала 50 дБ и значительной амплитудной и частотной модуляции возможно восстановление полной фазы квазигармонического сигнала с погрешностью не хуже 10–6 рад.
Формально, предложенный в работах [7 – 9] метод можно использовать и для измерения сдвига фаз двух квазигармонических сигналов как разности их полных фаз. Однако такой подход не является оптимальным, так как не использует априорную информацию о равенстве мгновенных частот исследуемых сигналов. В задачах же радиоинтерферометрии, акустики и ряде других часто приходится иметь дело с сигналами, полученными от одного источника, что является дополнительной априорной информацией при определении фазового сдвига сигналов.
Параметрический метод измерения разности фаз
Рассмотрим два квазигармонических сигнала:
![]() , (2)
, (2)
огибающие которых a1(t), a2(t) различны, а полные фазы отличаются на постоянную величину j0, при этом как полные фазы, так и огибающие отвечают условиям медленности изменения [7 – 9]:
![]() (3)
(3)
Искомыми параметрами сигналов являются частота и фазовый сдвиг, а амплитудная модуляция, выраженная в изменении огибающих a1(t), a2(t), представляет собой паразитное явление, которое необходимо скомпенсировать.
Пусть Δ – некоторый временной интервал, такой, что ω(t)Δ < π/4. При дискретизации сигнала с шагом Δt интервал Δ может содержать несколько интервалов Δt, то есть Δ = QΔt. Возьмем значения сигналов в точках (t – iΔ), (i = 0, ..., 4) и разложим их в ряд около центральной точки (t – 2Δ) с шагом Δ и 2Δ:
 (4)
(4)
Для простоты записи в (4) примем следующие обозначения:
a1(t – 2Δ) = a1, a2(t – 2Δ) = a2, θ(t – 2Δ) = θ, ω(t –2Δ) = ω.
Используя представление сигналов (4), составим две комбинации из их значений:
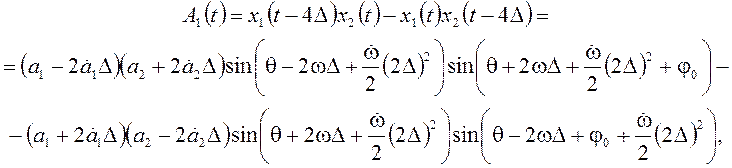
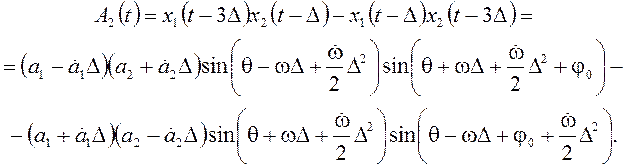
Окончательно получаем
 (5)
(5)
Здесь δ1(t) и δ2(t) – погрешности вычисления величин A1(t) и A2(t) соответственно, вызванные наличием шума и опущенных старших производных в разложении (4).
Отношение величин (5) дает выражение для оценки частоты
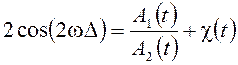 , (6)
, (6)
где ω = ω(t – 2Δ), χ(t) – погрешность, осциллирующая с частотой ω, амплитуда которой пропорциональна погрешностям δ1(t) и δ2(t).
Теперь рассмотрим отношение

где  . В приближении малости производной огибающей, отсюда следует
. В приближении малости производной огибающей, отсюда следует
 . (7)
. (7)
Аналогично рассмотрим отношение значений второго сигнала:

Отсюда с использованием соотношения (7) можно получить выражение для tg(φ0):
 , (8)
, (8)
где
 (9)
(9)
Выражая в равенстве (8) sin(2ωΔ) через cos(2ωΔ) и применяя формулу (6), получим выражение для оценки фазового сдвига сигналов в момент времени t:
 . (10)
. (10)
Для применения алгоритма (10) к цифровой системе перейдем к дискретному времени t = nΔt, n = 0,..., N – 1, Δ = QΔt. Тогда функции (5) и (9) примут вид

Здесь используется обозначение f[n] = f(nDt). Перепишем выражение (10) для дискретного времени:
 . (11)
. (11)
В данном случае оценка разности фаз квазигармонических сигналов получается по пяти отсчетам, что при наличии шума приведет к большой ошибке. Согласно рассматриваемой модели (4) φ0 является константой на рассматриваемом временном интервале. Последовательность χ[n] осциллирует с частотой ω, и ее среднее значение на интервале наблюдения T >> 2π/ω близко к нулю. Тогда с помощью метода наименьших квадратов, минимизируя ошибку
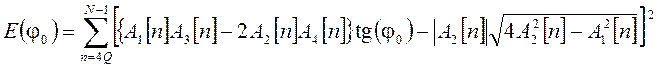 ,
,
получаем выражение для оценки сдвига фаз на выборке в Nотсчетов сигнала:
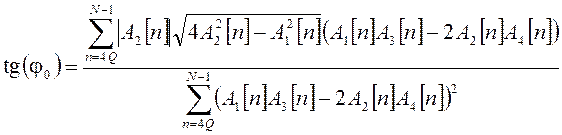 . (12)
. (12)
Заметим, что выражение (12) может использоваться не только на полной выборке данных, но и в пределах некоторого интервала наблюдения (окна).
Численное моделирование работы метода
Численное моделирование подтвердило возможность использования предлагаемого метода для оценивания фазового сдвига j0. В качестве примера на рисунке 1 представлена зависимость абсолютной погрешности определения фазового сдвига Δj = j – j0 на основе формулы (12) от заданного значения j0 для гармонических последовательностей
![]() .
.
Здесь φ – фазовый сдвиг, полученный в эксперименте, f0 = 0,031. Во всех представленных экспериментах N = 100000, Δt = 1, Q = 1, φ0 изменяется в диапазоне [0, π/2].
На рисунке 1 представлен результат моделирования для гармонических сигналов с медленно меняющимися огибающими
![]() ,
,
где γ1 = 0,0002, γ2 = 0,0002 и f0= 0,147.

Рисунок 1 – Зависимость абсолютного отклонения оценки фазового сдвига Δφ от значения φ0 для сигналов с амплитудной модуляцией
Как видно из рисунка 1, несмотря на существенное изменение амплитуды от начала до конца исследуемой выборки, ошибка восстановления заданной разности фаз φ0 не превышает 2∙10-6 рад при его изменении от 0 до π/2. При этом абсолютное отклонение резко возрастает на краю интервала.
Устойчивость метода к медленному изменению частоты иллюстрирует результат обработки сигналов с частотной модуляцией вида
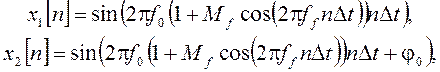
представленный на рисунке 2. Здесь f0 = 0,093, Mf = 0,15 и ff = 0,00053.

Рисунок 2 – Зависимость абсолютного отклонения оценки фазового сдвига Δφ от значения φ0 для сигналов с медленно меняющейся частотой
Аппаратно-программный комплекс
Экспериментальная установка для проверки работы описанного метода измерения фазового сдвига состоит из блока формирования сигналов (БФС), блока выходных фильтров нижних частот (БФНЧ), блока дискретизации сигналов (БДС) и персонального компьютера (ПК) (рисунок 3). Блок БФНЧ содержит прецизионные аналоговые элементы, помещенные в пассивный термостат. Это необходимо для того, чтобы дрейф их параметров не влиял на разность фаз сигналов.

Рисунок 3 – Структурная схема аппаратно-программного комплекса
БФС совместно с БФНЧ предназначен для генерации двух гармонических сигналов с переменными огибающими следующего вида:
 (13)
(13)
Здесь M1 и M2 – глубина амплитудной модуляции первого и второго каналов соответственно, fм1 и fм2 – частоты, φм1 и φм2 – фазы модулирующих сигналов, f1 и f2 – несущие частоты, φ1 и φ2 – фазы формируемых сигналов. Структурная схема БФС представлена на рисунке 4.

Рисунок 4 – Структурная схема БФС
Гармонические сигналы создаются цифровыми синтезаторами частоты ЦСЧ1 – ЦСЧ4, реализованными на основе микросхем прямого цифрового синтеза AD9835 [10]. Управление ЦСЧ осуществляется посредством ПК через микроконтроллер МК, который получает по шине USBкоманды и информацию для работы ЦСЧ. МК передает по последовательному интерфейсу каждому ЦСЧ информацию о частоте, фазе, а также режимах его работы. Тактирование МК и ЦСЧ происходит от внешнего источника опорной частоты 10 МГц. Сгенерированные сигналы проходят через полосовые фильтры Ф1 – Ф4 для удаления постоянной составляющей сигнала, сформированного ЦАП ЦСЧ, и частот, превышающих 1 МГц. Сигналы с выходов фильтров Ф2 и Ф4 с частотами f1 и f2 и сигналы с выходов фильтров Ф1 и Ф3 с частотами fм1 и fм2 поступают на сумматоры СУМ1 и СУМ2 соответственно, где к ним добавляется постоянный уровень напряжения, необходимый для осуществления амплитудной модуляции. С выходов смесителей сигналы подаются на БФНЧ, после которых принимают вид (13). Немодулированные сигналы с частотами f1 и f2 и постоянными амплитудами также подаются на выходы.
Частоты fм1, fм2, f1 и f2 задаются с помощью персонального компьютера в диапазоне от 1 Гц до 500 кГц, с абсолютной погрешностью ±1,16×10-6 Гц, начальные фазы φм1, φм2, φ1 и φ2 также задаются с помощью ПК в диапазоне от 0 до 2π с абсолютной погрешностью ±7,66×10-4 рад. Глубина модуляции для обоих каналов определяется параметрами схемы и может быть задана на уровне 20%, либо отключена. Уровень выходных сигналов составляет приблизительно 1 В.
Вторым компонентом комплекса является блок дискретизации сигналов, предназначенный для усиления сигналов, их оцифровки и передачи в ПК последовательностей данных. Прибор содержит два независимых канала. На рисунке 5 представлена структурная схема БДС.
Для усиления входных сигналов предназначены усилители У1 и У2, реализованные на прецизионных операционных усилителях. Для каждого из 16-разрядных АЦП1 и АЦП2 AD7671 [11] опорный уровень формирует свой источник опорного напряжения 2,5 В (ИОН1 и ИОН2). Дискретизация сигналов происходит синхронно по команде микроконтроллера МК. Прием данных из АЦП1 и АЦП2 микроконтроллером МК происходит поочередно по последовательной шине данных, после чего эти данные по шине USB поступают в ПК. Частота дискретизации БДС равна fd = 1250/241 = 5,1867219917 кГц.
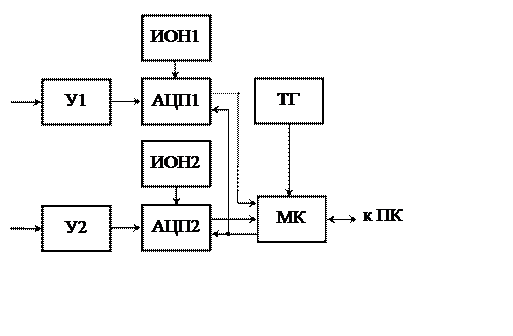
Рисунок 5 – Структурная схема БДС
Получение данных в ПК осуществляется при помощи интерфейсной программы, которая позволяет также передавать указанные параметры в микроконтроллеры БФС и БДС. В файлах с данными сохраняются условия эксперимента, количество отсчетов данных, время и дата начала эксперимента, а также примечание пользователя.
Программа для обработки полученных сигналов позволяет считать из файла данных частоты сигналов f1 и f2, частоту дискретизации fd, количество отсчетов N, а также последовательности x1[n] и x2[n] (n = 0, ..., N – 1).
Для улучшения соотношения сигнал/шум полученные последовательности перед обработкой пропускаются через цифровой полосовой фильтр с заданными частотами среза fmin и fmax. Импульсная характеристика h[m] (m = 0, ..., M – 1) КИХ-фильтра с линейной ФЧХ первого вида с нечетным Mрассчитывается методом взвешивания [12] с заданным временным окном w[m].
После фильтрации исходных последовательностей их обработка может производиться двумя способами. Первый предполагает оценивание разности фаз φ = φ1 – φ2 в соответствии с изложенным методом по всей имеющейся выборке данных, за исключением начального интервала [0, M – 1], соответствующего переходному процессу фильтра. Второй способ позволяет получить динамику разности фаз. Для этого задается длительность скользящего окна L, а оценки разности фаз вычисляются в рамках данного окна. Таким образом, получается последовательность φ[l], l = L + M – 1, ..., N – 1.
Результаты экспериментов
В ходе контрольного эксперимента к обоим входам БДС подключался прецизионный генератор сигналов Г3-122, формирующий гармонический сигнал с частотой 1 кГц. Длина выборок данных составляла N = 105 отсчетов, частота дискретизации БДС составляла fd = 5,1867219917 кГц, полоса пропускания цифрового фильтра Δf = fmax – fmin = 20 Гц. Обработка данных, результаты которой представлены на рисунках 6 и 7, производилась оконным методом при различной длине окна L.

Рисунок 6 – Динамика отклонения оценки разности фаз от среднего в эксперименте с Г3-122 при L = 1001

Рисунок 7 – Динамика отклонения оценки разности фаз от среднего в эксперименте с Г3-122 при L = 10001
Зависимость среднеквадратичного отклонения σΔφ, рассчитанного по всей выборке при тех же условиях эксперимента, от длины окна показана на рисунке 8.

Рисунок 8 – Зависимость СКО отклонения оценки разности фаз в эксперименте с Г3-122 от длины окна L
Приведенные результаты показывают, что увеличение размера скользящего окна данных приводит к улучшению точности восстановления разности фаз на идеальных сигналах, что позволяет достичь точности не хуже 10-6 рад.
В таблице 1 приведено сравнение оценок разности фаз сигналов с несущей частотой f0 = 1 кГц с амплитудной модуляцией и без нее, полученных с помощью БФС. Здесь K – число выборок по 105 отсчетов, учтенных в статистике, σΔφ – дисперсия значений фазы, рассчитанных по этим выборкам, σΔφ с – среднее дисперсий оценок разности фаз, полученных оконным методом с длиной окна L = 1001. Глубина амплитудной модуляции составляла порядка 20%.
Таблица 1 – Оценки разности фаз сигналов БФС
Δφзад, рад | Без амплитудной модуляции | С амплитудной модуляцией | ||||
K | σΔφ, 10-6 рад | σΔφ с,10-6 рад | K | σΔφ, 10-6 рад | σΔφ с,10-6 рад | |
0 | 4 | 4,17 | 7,45 | 5 | 37,9 | 83,7 |
0,26231071 | 22 | 6,05 | 10,6 | 17 | 26,7 | 79,4 |
0,78539816 | 19 | 7,84 | 20,8 | 16 | 27,9 | 79,2 |
Выводы
Разработанный метод позволяет измерять разность фаз сигналов с медленно меняющимися амплитудой и частотой по ограниченным выборкам с точностью не хуже 10-6, а при наличии амплитудной модуляции – не хуже 5∙10-5. Полученные результаты позволяют использовать данный метод в различных задачах радиотехники, в том числе прецизионной радиоинтерферометрии на базе навигационных систем GPS, ГЛОНАСС, ГАЛИЛЕО [13].
Предложенный параметрический метод целесообразно применять в системах реального времени, где точное значение фазового сдвига требуется получить за короткое время по ограниченному числу периодов сигнала и его отсчетов. В таких условиях рассматриваемый алгоритм может быть наиболее эффективным в сравнении с другими аналогичными цифровыми алгоритмами определения фазового сдвига [2, 5].
Работа выполнена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы, проекты № 14.В37.21.07284 и № 14.В37.21.0736.
Список литературы
1. Маковецкий П.В., Олянюк В.П. Фазовые методы измерения дальности. Л.: Ленинградский институт авиационного приборостроения, 1989. 44 с.
2. Чмых М.К. Цифровая фазометрия. М.: Радио и связь, 1993. 184 с.
3. Марпл-мл. С.Л. Цифровой спектральный анализ и его приложения. М.: Мир, 1990. 584 с.
4. Марченков С.С., Матросов В.Л. Сложность алгоритмов и вычислений // Итоги науки и техн. Сер. Теория вероятностей и математическая статистика. Теоретическая кибернетика. Т. 16. М.: ВИНИТИ, 1979. С. 103-149.
5. Смирнов В.Н., Кучеров М.В. Широкополосный цифровой фазометр // Вопросы радиоэлектроники. 2004. № 1. С. 33-41.
6. ГОСТ 8.567-99. Государственная система обеспечения единства измерений. Измерение времени и частоты. Термины и определения. Введ. 01.01.2001. М.: Изд-во стандартов, 2000. 11 с.
7. Игнатьев В.К., Никитин А.В., Юшанов С.В. Параметрический анализ колебаний с медленно меняющейся частотой // Известия вузов. Радиофизика. 2010. Т. 53, № 2. C. 145-159.
8. Игнатьев В.К., Никитин А.В. Метод медленно меняющейся частоты в радиоволновых измерениях // Журнал радиоэлектроники. 2011. № 11. Режим доступа: http://jre.cplire.ru/jre/nov11/17/text.pdf (дата обращения 01.06.2013).
9. Боровков В.И., Игнатьев В.К., Никитин А.В., Юшанов С.В. Однозначное определение огибающей и мгновенной частоты электромеханических колебаний // Известия вузов. Электромеханика. 2012. № 1. С. 16-20.
10. Техническая документация на микросхему AD9835 [50 MHz Direct Digital Synthesizer, Waveform Generator AD9835]. Режим доступа: http://www.analog.com/static/imported-files/data_sheets/AD9835.pdf (дата обращения 20.11.2012).
11. Техническая документация на микросхему AD7671 [16-Bit, 1 MSPS CMOS ADC. AD7671]. Режим доступа: http://www.analog.com/static/imported-files/data_sheets/AD7671.pdf (дата обращения 20.11.2012).
12. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов : пер. с англ. М.: Мир, 1978. 848 с.
13. ГЛОНАСС. Принципы построения и функционирования / Под ред. А.И. Перова, В.Н. Харисова. М.: Радиотехника, 2010. 800 с.
Публикации с ключевыми словами: аппаратно-программный комплекс, фазовые измерения, квазигармонический сигнал, измерения в реальном времени
Публикации со словами: аппаратно-программный комплекс, фазовые измерения, квазигармонический сигнал, измерения в реальном времени
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



