научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#8 август 2006
МЕТОДЫ ОПТИМИЗАЦИИ
А. Ю. Щеглов, д-р техн. наук, проф СПбГИТМО (ТУ)
Векторный метод решения задачи линейного программирования; с пошаговым усечением множества "нехудших решений"
Рассматривается интерпретация задачи линейного программирования как пошаговой задачи многокритериальной оптимизации. Приводится векторная интерпретация критерия оптимальности, гарантирующего поиск оптимального решения. Предлагается пошаговый метод усечения получаемого на каждом шаге решения задачи множества "нехудших решений" и метод решения задачи, гарантирующий нахождение оптимального решения при снижении сложности вычислений за счет усечений множеств "нехудших решений".
Задача линейного программирования в общем виде может быть представлена следующим образом. Найти xn, n = 1, ..., N такие, что

при условии, что

при хп ![]() . При необходимости дополняется условие целочисленности всех xn.
. При необходимости дополняется условие целочисленности всех xn.
Рассмотрим интерпретацию задачи линейного программирования как пошаговую задачу многокритериальной оптимизации. В общем случае задача многокритериальной оптимизации может быть сформулирована следующим образом. Задано N вариантов системы, с номерами n = 1, ..., N, каждый из которых характеризуется M параметрами (или частными критериями качества) qnm с номерами m = 1,..., M. Требуется выбрать вариант, превосходящий остальные варианты по совокупности параметров.
Задача линейного программирования может интерпретироваться как задача многокритериальной оптимизации в следующем смысле [1, 2]. Задано N вариантов, характеризуемых М параметрами qnm с номерами m = 1, ..., М. На каждом шаге требуется выбрать оптимальный вариант (план) из заданного множества (из N) вариантов. Оптимальность здесь понимается в смысле наилучшего достижения совокупности ограничений Qm, m = 1, ..., М, при использовании выбранного варианта. Если рассмотреть некоторый произвольный шаг оптимизации, то он отличается от предыдущего лишь тем, что требуется уже выполнить ограничения m-типов, задаваемых не параметрами Qm, а в общем случае меньшими значениями, с учетом полученных на предыдущих шагах результатов. Для рассматриваемого шага решаем многокритериальную задачу — выбрать оптимальный вариант по совокупности M параметров. Очевидно, что реализуемый метод нормирования параметров должен учитывать, в какой мере для каждого шага достигаются заданные ограничения Qm.
Таким образом, предлагается интерпретировать задачу линейного программирования как пошаговую задачу многокритериальной оптимизации (по M параметрам). Отличие выбора оптимального решения здесь состоит в том, что ограничения имеют единый физический смысл, что не требует нормирования однородных параметров в целях приведения их к безразмерному виду.
Для выбора на каждом
шаге оптимального варианта может быть использован рассмотренный в [3] подход для
выбора "нехудших решений" в векторном пространстве критериев. Этот подход состоит
в учете при оптимизации вариантов одновременно двух критериев оптимальности —
длину вектора качества варианта Xn и угол ![]() между векторами варианта и некоторым идеальным вектором (обозначим
его n = 0), представляющим собой, по существу, некоторое
идеальное качество:
между векторами варианта и некоторым идеальным вектором (обозначим
его n = 0), представляющим собой, по существу, некоторое
идеальное качество:

При выборе оптимального
варианта ![]() . Это имеет физический
смысл выбора не худших решений, качество которых в M-мерном
пространстве отображается векторами, имеющими максимальную длину и наилучшим образом
совпадающими по направлению с заданным идеальным вектором. Однозначное отображение
качества варианта вектором в пространстве критериев возможно, так как любой вариант
некоторой системы, вообще говоря, всегда может быть охарактеризован двумя критериями
— совокупным качеством (значениями отдельных параметров варианта) и соответствием
этого совокупного качества требованиям пользователя системы.
. Это имеет физический
смысл выбора не худших решений, качество которых в M-мерном
пространстве отображается векторами, имеющими максимальную длину и наилучшим образом
совпадающими по направлению с заданным идеальным вектором. Однозначное отображение
качества варианта вектором в пространстве критериев возможно, так как любой вариант
некоторой системы, вообще говоря, всегда может быть охарактеризован двумя критериями
— совокупным качеством (значениями отдельных параметров варианта) и соответствием
этого совокупного качества требованиям пользователя системы.
Если рассмотреть векторную интерпретацию сказанного, то совокупное качество системы отображается длиной вектора в пространстве критериев, а способность удовлетворения этим качеством требованиям пользователя системы, отображаемым в векторном пространстве некоторым идеальным вектором (направлением и длиной), можно учесть величиной угла между рассматриваемыми векторами — совокупного качества системы и идеального.
Замечание. В рассматриваемых
формулах используются нормированные (безразмерные) значения параметров q0m, qnm, где
![]() , что в задачах многокритериальной
оптимизации реализуется в целях учета значений параметров, имеющих различный физический
смысл. С учетом сказанного получаем:
, что в задачах многокритериальной
оптимизации реализуется в целях учета значений параметров, имеющих различный физический
смысл. С учетом сказанного получаем:
 (1)
(1)
Рассмотренный подход
в задачах многокритериальной оптимизации представляет теоретический интерес, так
как гарантирует, что в найденном множестве "нехудших решений" обязательно будет присутствовать
и оптимальный вариант. Однако на практике в задачах многокритериальной оптимизации
использование обоих критериев оптимальности существенно усложняет решение задачи,
поскольку, как правило, позволяет найти множество "нехудших решений", которое может
отличаться большой мощностью. Поэтому в [4—9] в качестве критерия оптимальности
нами предлагается использовать только один параметр Xn0
— длина проекции вектора качества варианта на идеальный вектор, который позволяет
одновременно учитывать оба параметра Xn и ![]() , т. е. свести задачу оптимизации к однокритериальной
, т. е. свести задачу оптимизации к однокритериальной
![]()
при условии выбора оптимального варианта
![]() . В [4] строго доказывается,
что в ортонормированном базисе вместо длины проекции на идеальный вектор может рассматриваться
аддитивная свертка нормированных значений параметров, представляющая собой сумму
нормированных параметров вариантов, использование которой существенно упрощает решение
задачи при векторной ее интерпретации. Однако использование данного критерия в общем
случае не гарантирует нахождения оптимального решения (в общем случае здесь может
быть осуществлен поиск решения, близкого к оптимальному, в кратчайшие сроки, что
делает данный подход весьма эффективным в задачах оперативного планирования работ
[1]).
. В [4] строго доказывается,
что в ортонормированном базисе вместо длины проекции на идеальный вектор может рассматриваться
аддитивная свертка нормированных значений параметров, представляющая собой сумму
нормированных параметров вариантов, использование которой существенно упрощает решение
задачи при векторной ее интерпретации. Однако использование данного критерия в общем
случае не гарантирует нахождения оптимального решения (в общем случае здесь может
быть осуществлен поиск решения, близкого к оптимальному, в кратчайшие сроки, что
делает данный подход весьма эффективным в задачах оперативного планирования работ
[1]).
В основу векторной интерпретации задачи линейного программирования, как пошаговой задачи синтеза плана, может быть положена рассмотренная векторная интерпретация задачи многокритериальной оптимизации. Векторная интерпретация задачи на плоскости (в пространстве RM=2) проиллюстрирована на рис. 1. Здесь по осям координат, где откладываются параметры для различных вариантов плана qm, отложены и ограничения Qm.
В приведенной системе координат получаем вектор <00'>, образующий идеальное направление "продвижения в пространстве критериев" для выполнения заданных ограничений (идеальность направления соответствует равенству Qm в исходной системе ограничений). Два возможных плана (N = 2) отображаются в рассматриваемом пространстве векторами, например <001> и <002>. Метод поэтапного получения оптимального плана (векторный метод планирования) состоит в выборе на каждом этапе оптимизации лучшего вектора по критериям — длина вектора и угол с идеальным вектором <00'>, с переносом системы координат в направлении и на длину выбранного на очередном этапе оптимизации вектора. В частности, на рис. 1 лучшим для рассматриваемого этапа составления плана (при наличии двух вариантов) будет вариант, отображаемый вектором <001>. Отложив этот вектор, получим новую систему координат и соответствующий ей новый идеальный вектор <0*0'>, который примем в качестве вектора, задающего идеальное направление для следующего этапа. Многошаговая процедура завершается при выполнении ограничений по всем видам задач. Набор последовательностей отложенных векторов на всех шагах оптимизации и соответствует оптимальному плану.
Замечание. При альтернативной постановке задачи линейного программирования — найти xn, x = 1,…, N, такие, что

при условии, что
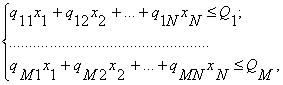
необходимо уже, наоборот, достигнуть
разрешенной области за максимальное число шагов. Здесь критерием оптимальности также
остаются параметры Xn и ![]() , но условием выбора оптимального плана уже будет
, но условием выбора оптимального плана уже будет
![]() и
и ![]() для каждого этапа оптимизации, причем оптимизация
будет заканчиваться выполнением предпоследнего шага — на последнем вектор пересечет
запретную область.
для каждого этапа оптимизации, причем оптимизация
будет заканчиваться выполнением предпоследнего шага — на последнем вектор пересечет
запретную область.
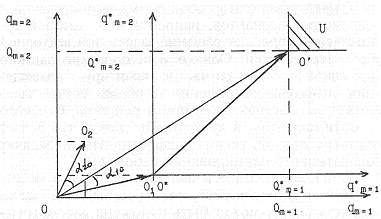
Рис. 1. Иллюстрация векторной интерпретации задачи линейного программирования на плоскости
Теперь остановимся на вопросах синтеза ортонормированного базиса. При объективном способе нормирования параметров [4, 9] в качестве идеальных выбираются лучшие значения параметров на сравниваемом множестве вариантов n = 1, ..., N, задаваемые в рассматриваемом случае формулой
![]()
причем на сравниваемом множестве вариантов N = 1,..., N корректируются значения параметров, качество которых превосходит задаваемое (или требуемое) идеальное, — приравниваются задаваемому идеальному. Нормированные значения параметров задаются формулами.
![]()
Задание весовых
коэффициентов ![]() может быть
интерпретировано следующим образом: изменение весовых коэффициентов рт изменяет направление
и длину гипотетически идеального вектора в пространстве критериев. При этом соответственно
изменяются и значения углов векторов вариантов с идеальным вектором, т. е. значения
одного из критериев оптимальности. Так как весовые коэффициенты
может быть
интерпретировано следующим образом: изменение весовых коэффициентов рт изменяет направление
и длину гипотетически идеального вектора в пространстве критериев. При этом соответственно
изменяются и значения углов векторов вариантов с идеальным вектором, т. е. значения
одного из критериев оптимальности. Так как весовые коэффициенты ![]() используются для того, чтобы учесть различие
ограничений Qm, они вычисляются по формуле
используются для того, чтобы учесть различие
ограничений Qm, они вычисляются по формуле
![]()
где
![]()
Именно такой подход к нормированию параметров нами предлагался для оперативного решения систем линейных уравнений большой размерности [2] и для приложений задач линейного программирования, используемых для решения задачи распределения работ в мультипроцессорных системах, решаемых в рамках теории расписаний [1].
При нормировании
параметров целевой функции необходимо учитывать, в какой мере по сравнению с вариантом,
характеризуемым ![]() , увеличит
значение целевой функции любой иной n-й вариант. С
учетом сказанного имеем:
, увеличит
значение целевой функции любой иной n-й вариант. С
учетом сказанного имеем:

Векторная интерпретация
использования коэффициента ![]() также
связана с изменением расположения области ограничений и, как следствие, идеального
вектора в пространстве критериев.
также
связана с изменением расположения области ограничений и, как следствие, идеального
вектора в пространстве критериев.
С учетом сказанного векторный пошаговый метод получения оптимального плана состоит в следующем. На каждом шаге оптимизации необходимо проверять условие выполнения заданных ограничений Qm. Если они не выполняются, осуществляется очередной шаг. При выполнении каждого шага оптимизации фиксируется выбранный оптимальный вектор, пересчитываются новые ограничения Qm (что эквивалентно отложению вектора в пространстве критериев), M = 1,..., М:
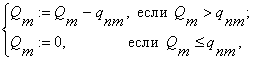
рассчитываются и сравниваются значения критериев оптимальности, оптимальный вариант (частный план) выбирается на каждом шаге на основании приведенных выше условий оптимальности. Формальным условием окончания пошаговой процедуры оптимизации будет выполнение условия Qm: = 0, m = 1,..., М. Решением задачи будет множество планов, составляющих множество "нехудших решений", соответствующих последовательности отложенных на всех шагах оптимальных векторов.
Утверждение. Вместо
критерия ![]() отличающегося
сложностью вычислений при многошаговой процедуре, может быть использован критерий
Yn вычисляемый по более простой формуле
отличающегося
сложностью вычислений при многошаговой процедуре, может быть использован критерий
Yn вычисляемый по более простой формуле
где Xn — другой критерий оптимальности (длина вектора варианта).
Доказательство.
Утверждение доказывается тем, что функция y = arccosx монотонно убывает на рассматриваемой области определения
(ее график — часть косинусоиды, зеркально отображенной относительно прямой
x - y
= 0), в качестве критерия оптимальности ![]() ,
задаваемого формулой (1), может быть использован более простой для расчетов критерий
,
задаваемого формулой (1), может быть использован более простой для расчетов критерий

откуда получаем
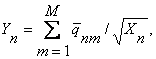
Таким образом,
при синтезе плана в ортонормированном базисе имеем два критерия оптимальности Xn и Yn
с использованием которых условие выбора оптимальных решений принимает вид ![]() и
и ![]() .
.
Теперь остановимся на рассмотрении проблемы пошаговых усечений определяемых множеств "нехудших решений". На рис. 1 по обоим критериям оптимальности был однозначно определен оптимальный вектор. Теперь рассмотрим случай, проиллюстрированный на рис. 2, когда по одному критерию лучшим оказывается один вектор качества (<001> по Xn), по другому критерию — другой вектор (<002> по Yn). Получается, что на первом шаге оптимизации оба варианта составляют множество нехудших решений , так как по совокупности двух критериев здесь не может быть однозначно выбрано оптимальное решение. Чтобы гарантировать нахождение оптимального плана, следующий шаг уже необходимо рассмотреть для обоих решений, получаемых на первом шаге (в общем случае — для всех вариантов, составляющих множество "нехудших решений"). На втором шаге также в общем случае находим ограниченное множество "нехудших решений" для каждого из векторов, отложенных на первом шаге и т. д. Это приводит к существенному увеличению сложности решения, что обусловливает актуальность постановки и решения задачи усечения получаемых множеств "нехудших решений".

Рис. 2. Иллюстрация поиска ограниченного множества "нехудших решений"
Естественно, что наиболее радикален в этом смысле предложенный нами метод сведения задачи к одно критериальной, однако данный подход не позволяет гарантировать нахождение оптимального плана [1].
В данной статье предлагается альтернативный метод пошаговых усечений множеств "нехудших решений", состоящий в следующем. Будем проводить усечение найденных множеств не для отдельного шага оптимизации, что делается при сведении задачи к однокритериальной, а на последовательности шагов. При этом реализуется следующая идея. Заменим на втором шаге получаемые последовательности отложенных на первых двух шагах векторов одним вектором. Для новых векторов вновь проведем сравнение с использованием критериев Xn и Yn, определяя "нехудшие решения" уже из вновь полученных векторов, которые и будут использоваться на третьем шаге, причем в качестве идеального вектора вновь рассматривается исходный идеальный вектор, который использовался на первом шаге оптимизации. На третьем шаге вновь приводим векторы и корректируем множество "нехудших решений".
Таким образом, идея метода пошаговых усечений множества "нехудших решений" состоит в том, чтобы на каждом (после первого) шаге отложенные последовательности векторов заменить одним вектором, исходящим из вершины исходной системы координат, с последующим анализом приведенных векторов. При этом в качестве идеального вектора на всех этапах усечения множества "нехудших решений" должен приниматься исходный идеальный вектор, так как на любом шаге приведенные векторы выходят из исходной системы координат.
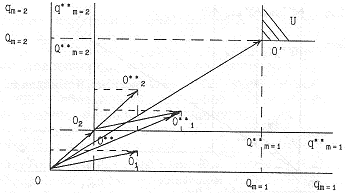
Рис. З. Иллюстрация метода пошаговых усечений множества "нехудших решений"
Идея данного метода проиллюстрирована на рис. 3, где на втором шаге для отложенного на первом шаге вектора <002> (на первом шаге оба вектора <001> и <002> составляют множество "нехудших решений") получаем приведенные векторы <001**> и <001**>, где вектор <001**> по совокупности обоих критериев оптимальности превосходит вектор <002**>, или план, отображаемый в пространстве параметров вектором <001**>, лучше плана, отображаемого вектором <002**>. Делаем вывод, что вектор <002>, откладываемый на втором этапе, не составляет множество "нехудших решений', так как он исключается нами из данного множества в результате реализации метода пошаговых усечений искомого множества решений.
Таким образом, особенностью предлагаемого подхода к уменьшению мощности получаемого множества "нехудших решений" является дополнительная оптимизация (кроме пошагового сравнения вариантов), состоящая в сравнении частей получаемых на каждом шаге планов, представляющих собой последовательности получаемых на всех предшествующих шагах (включая первый) "нехудших решений".
Таким образом, к достоинствам предлагаемого метода решения задачи линейного программирования, представляющего собой метод комбинаторного программирования (кстати говоря, как любой иной метод решения данной задачи, включая и симплекс-метод), в основу которого положена векторная интерпретация задачи линейного программирования и многокритериальной задачи оптимизации, интерпретация задачи линейного программирования как пошаговой многокритериальной задачи оптимизации, можно отнести следующее:
· на каждом шаге осуществляется направленный выбор решения, что обусловливает возможность решения задачи за минимальное число шагов;
· на каждом шаге гарантируется, что оптимальное решение войдет в найденное множество "нехудших решений";
· на каждом шаге реализуются простейшие вычисления критериев оптимальности Xn и Yn что обусловливает низкую вычислительную сложность метода;
· метод предполагает возможность пошаговых усечений искомых множеств "нехудших решений", что также уменьшает его вычислительную сложность.
К достоинствам метода можно также отнести его эффективность для решения наиболее сложных приложений задач линейного программирования — целочисленной задачи. Это означает, что векторы откладываются на каждом шаге, кроме последнего, полностью. Тогда все получаемые планы, составляющие усеченное множество "нехудших решений", определяемые на последнем шаге, не могут быть сравнены между собой, т. е. они эквивалентны.
Для решения задачи линейного программирования, не требующей целочисленности решения, может быть применен метод поэтапного приближения [2], который состоит в решении задачи в несколько этапов: на первом задача решается целочисленно, на втором задача оптимизации решается в противоположном квадранте, где "нехудшие векторы" откладываются не полностью, а лишь их k-я часть, k < 1. Окончанием выполнения этапа будет выход из допустимой области решений. После этого осуществляется возврат к решению задачи в исходном квадранте, к уменьшается. Задача (выполнение этапов, каждый из которых характеризуется уменьшением коэффициента к и сменой квадранта, в котором решается оптимизационная задача) завершается при точном ее решении, либо при ее решении с заданной точностью, при котором система ограничений принимает вид не менее Qm, но менее, чем Qm + Qm.
Список литературы
1. Щеглов А. Ю. Векторные интерпретация и метод решения задачи линейного программирования // Информационные технологии. 1998. № 8. С. 24—29.
2. Щеглов А. Ю. Векторная интерпретация и численный метод решения системы линейных уравнений // Изв. вузов. Приборостроение. 1993. № 9—10. С. 36—44.
3. Кузьмин Б. И., Русин Ю. С. Векторная оптимизация систем и аппаратуры радиосвязи // Электросвязь. 1986. № 5. С. 30-32.
4. Щеглов А. Ю. Методика векторной оптимизации сложных подсистем информационно-вычислительных сетей // Автоматика и вычислительная техника. 1988. № 5. С. 14—19.
5. Щеглов А. Ю. Дополнительный критерий для формального выбора оптимального варианта ЛВС из множества "нехудших решений" // Автоматика и вычислительная техника. 1991. № 4. С. 39-41.
6. Щеглов А. Ю. Метод многокритериальной оптимизации сложных систем с экспертным заданием гипотетически идеального вектора качества // Изв. вузов. Приборостроение. 1994. Т. 37. С. 21-23.
7. Щеглов А. Ю. Метод ограничений для оптимизации сложных систем // Радиотехника. [993. № 4. С. 9—13.
8. Щеглов А. Ю. Метод поинтервального учета неравнозначности разнородных параметров альтернативных вариантов сложных систем вычислительной техники // Автоматика и вычислительная техника. !990. № 6. С. 10—13.
9. Щеглов А. Ю. Статистический метод нормирования и учета относительной важности разнородных параметров для многокритериальной оптимизации сложных радиотехнических систем//Радиотехника. 1995. № 3. С. 7—9.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 7, 1999
МЕТОДЫ ОПТИМИЗАЦИИ
Публикации с ключевыми словами: Линейное программировани, многокритериальная оптимизация, пошаговые методы, усечение множества «нехудших решений»
Публикации со словами: Линейное программировани, многокритериальная оптимизация, пошаговые методы, усечение множества «нехудших решений»
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



