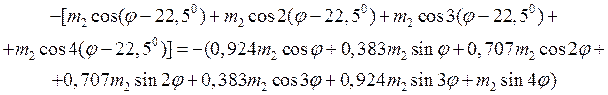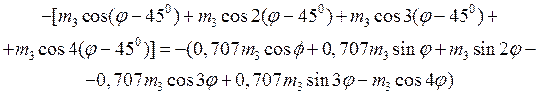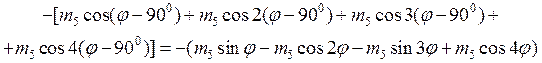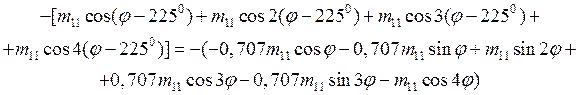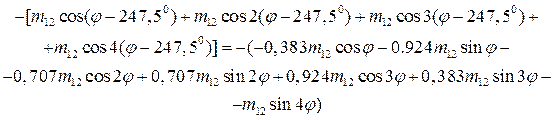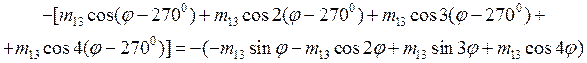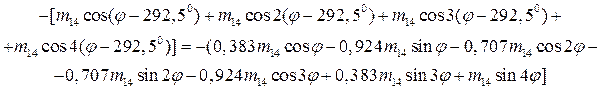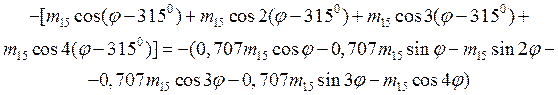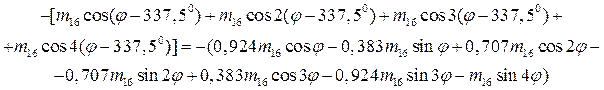научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 06, июнь 2013
DOI: 10.7463/0613.0579179
УДК 531.383
Россия, МГТУ им. Н.Э. Баумана
Россия, МГУ им. М.В. Ломоносова
Россия, ОАО Арзамасское НПО "Темп-Авиа"
Введение
Разработка недорогих волновых твердотельных гироскопов (ВТГ) с металлическими резонаторами началась в середине 1990-х гг. [1]. В настоящее время эквивалентная погрешность этих ВТГ составляет порядка 1 0/час, что позволяет строить на их основе бесплатформенные инерциальные навигационные системы (БИНС) низкой и средней точности широкого применения [2]. Погрешность ВТГ определяется рядом факторов, в том числе массовым дисбалансом резонатора, который вызван отклонением геометрии резонатора от идеальной осесимметричной формы и приводит к появлению дрейфа волновой картины в ВТГ, а также вибрационной чувствительности прибора [3]. Для устранения массового дисбаланса резонатор необходимо балансировать по четырем нижним формам массового дефекта. В литературе описаны различные технологии балансировки резонаторов из кварцевого стекла с использованием ионного травления [4] и лазерного испарения [5] для удаления неуравновешенной массы. Эти технологии позволяют решить данную задачу, но характеризуются большой трудоемкостью и сложностью применяемого оборудования.
Цель данной работы заключается в разработке простой и недорогой технологии балансировки металлических резонаторов, пригодной для использования в массовом производстве приборов.
1 Конструкция ВТГ
Конструктивно резонаторы ВТГ можно условно разбить на две группы: зубчатые и беззубцовые. Балансировка зубчатых резонаторов осуществляется путем удаления несбалансированной массы со специальных балансировочных зубцов [6]. Эта операция может проводиться, например, с помощью лазерного испарения. Хотя при этом структура материала зубца существенно нарушается, диссипативные характеристики резонатора не меняются, благодаря тому, что при колебаниях резонатора зубцы практически не деформируются. Трудоемкость балансировки зубчатых резонаторов может быть низкой, однако изготовление зубцов само по себе является достаточно сложной технологической операцией.
При балансировке беззубцовых резонаторов неуравновешенная масса удаляется непосредственно с рабочей поверхности. Очевидно, что этот подход требует использования методов обработки материала, не нарушающих существенно его структуры, в связи с чем удаление материала с поверхности оболочки резонатора идет с гораздо меньшей скоростью, чем с поверхности зубцов. Кроме того, удаление материала оболочки приводит не только к изменению распределения массы по окружному углу, но и изменению жесткости. Положительной стороной этого подхода является упрощение конструкции резонатора и технологии его изготовления благодаря отсутствию зубцов.
Так как обработка металла значительно проще обработки кварцевого стекла, металлические резонаторы ВТГ целесообразно изготавливать в зубчатом варианте, это позволяет существенно уменьшить трудоемкость балансировки. Для определения параметров массового дисбаланса можно использовать известные методы (см., например, [4]), в сочетании с использованием новых технологий удаления материала и алгоритмов балансировки. На рисунке 1 показана конструкция зубчатого резонатора, использованного в экспериментах.
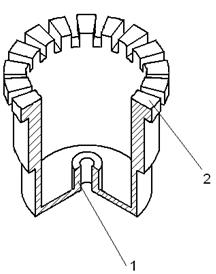
1 – крепежная ножка; 2 – балансировочный зубец
Рисунок 1 – Конструкция зубчатого металлического резонатора ВТГ
При использовании нержавеющей стали в качестве материала резонатора, частота колебаний по 2-й форме лежит в пределах 4,2–4,3 кГц.
2 Технология балансировки
Для удаления неуравновешенной массы использован электрохимический метод [7]. Резонатор 1 погружается в многоместную электрохимическую ванну, при этом каждый зубец погружен в электролит 2 отдельной электрохимической ячейке (рисунки 2, 3). Корпус ванны выполнен из фторопласта и имеет секции (по числу зубцов), отделенные друг от друга тонкими перегородками. В донную часть каждой секции ввернут электрод 3, подключенный к системе электропитания. Для электрохимического растворения металла на него подается постоянное напряжение от источника тока 4 через выключатель 5. Резонатор 1 электрически подключается отдельным проводом к общей шине.
Согласно закону Фарадея количество удаленного металла прямо пропорционально электрическому заряду, прошедшему через обрабатываемую поверхность. Для удаления массы mi с i-го балансировочного зубца через его поверхность надо пропустить заряд Qi , равный
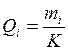 , (1)
, (1)
где K – постоянный коэффициент.

Рисунок 2 – Секционированная травильная ванна для электрохимической обработки резонатора

1 – резонатор; 2 – электролит; 3 – электрод; 4 – источник тока; 5 – выключатель
Рисунок 3 – Электрохимическое растворение металла с поверхности зубца
Коэффициент K определяют экспериментально по потере массы за единицу времени электрохимического растворения. Величину пропускаемого через поверхность зубца iэлектрического заряда Qi контролируют временем пропускания ti постоянного тока I:
 . (2)
. (2)
Величина тока I определяется по формуле:
![]() , (3)
, (3)
где S – площадь поверхности балансировочного зубца, 𝜌 – плотность тока, рекомендуемая для конкретного состава электролита и температуры электрохимического растворения [8].
В качестве электролита могут быть использованы любые электролиты, используемые для электрохимического растворения. Предпочтительны кислотные электролиты, обеспечивающие растворение продуктов, образующихся при электрохимическом растворении металла. После электрохимической обработки резонатор промывают дистиллированной водой и сушат.
Согласно (1)–(3), точность удаления массы с балансировочного зубца определяется нестабильностью тока I, проходящего через его поверхность и ошибкой во времени обработки ti. На практике погрешность этих величин не превышает 0,01-0.1%, что обеспечивает высокую точность удаления неуравновешенной массы. Достоинством разработанного метода является возможность удаления любого количества материала с любого зубца, при этом обработка всех зубцов может вестись одновременно, что позволяет значительно уменьшить общее время балансировки.
На рисунке 4 в качестве примера приведено изменение расщепления собственной частоты в ходе электрохимического удаления неуравновешенной массы.
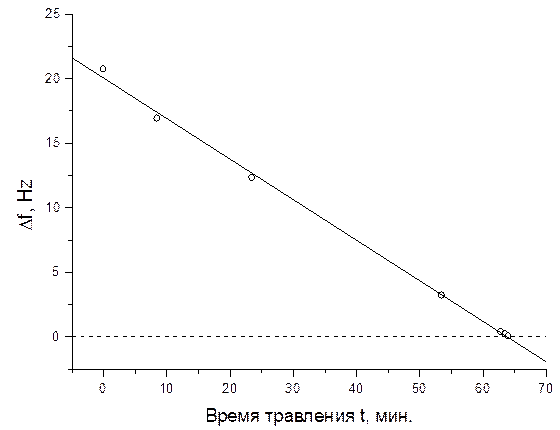
Рисунок 4 – Изменение расщепления собственной частоты резонатора из нержавеющей стали в ходе электрохимического удаления неуравновешенной массы
Первоначальное значение расщепления собственной частоты составляло 20,7 Гц, конечное – 0,03 Гц. Как показывает рисунок 4, удаленная масса зависит от времени обработки практически линейно. Электрохимическое удаление материала позволяет достаточно просто осуществить и балансировку первых трех форм массового дефекта.
3 Алгоритм балансировки ВТГ
Рассмотрим известный алгоритм балансировки резонатора путем удаления точечных масс [9]. Распределение массы оболочки резонатора вдоль окружного угла φ при удалении с нее точечной массы ∆m, расположенной в направлении φ=0, может быть описано разложением в ряд Фурье δ-функции [10]
 . (4)
. (4)
Рассмотрим проблемы, возникающие при балансировке резонатора этим методом. Пусть, например, необходимо устранить 1-ю форму массового дефекта величиной М1 (ее ориентацию относительно резонатора для простоты примем равной нулю). Удаление с кромки резонатора точечной массы  (в направлении φ = 0) устраняет ее, но одновременно создает такие же по величине 2-ю, 3-ю и 4-ю формы массового дефекта, которые необходимо устранять, причем их последующая балансировка также будет сопровождаться появлением кратных гармоник. Так, балансировка 2-й формы массового дефекта двумя точечными массами будет сопровождаться появлением 4-й формы, балансировка 3-й – появлением 6-й и т.д. То есть в этом случае устранение любой формы массового дефекта требует удаления строго определенного количества материала в нескольких точках. Например, устранение массового дефекта 1-й формы вида
(в направлении φ = 0) устраняет ее, но одновременно создает такие же по величине 2-ю, 3-ю и 4-ю формы массового дефекта, которые необходимо устранять, причем их последующая балансировка также будет сопровождаться появлением кратных гармоник. Так, балансировка 2-й формы массового дефекта двумя точечными массами будет сопровождаться появлением 4-й формы, балансировка 3-й – появлением 6-й и т.д. То есть в этом случае устранение любой формы массового дефекта требует удаления строго определенного количества материала в нескольких точках. Например, устранение массового дефекта 1-й формы вида ![]() требует удаления масс в 10-ти точках (рисунок 5) [9].
требует удаления масс в 10-ти точках (рисунок 5) [9].
Рассмотрим в качестве примера устранение 1-й формы массового дефекта резонатора вида ![]() . Пусть резонатор имеет 24 балансировочных зубца, причем положение центра зубца №1 соответствует направлению φ = 0. Примем также, что ширина зубца равна интервалу между ними. Учитывая, что ориентация массового дефекта в общем случае не совпадает с ориентацией зубцов, перепишем выражение массового дефекта резонатора в виде
. Пусть резонатор имеет 24 балансировочных зубца, причем положение центра зубца №1 соответствует направлению φ = 0. Примем также, что ширина зубца равна интервалу между ними. Учитывая, что ориентация массового дефекта в общем случае не совпадает с ориентацией зубцов, перепишем выражение массового дефекта резонатора в виде
![]() . (5)
. (5)
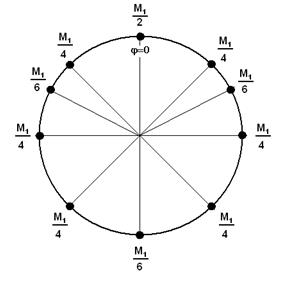
Рисунок 5 – Схема удаления точечных масс при балансировке 1-й формы массового дефекта
Из (5) следует, что для балансировки зубчатого резонатора по 1-й форме необходимо отдельно удалить его косинусную и синусную составляющие. Кроме того, необходимо учитывать, что представление (4) справедливо именно для точечного, в математическом смысле, удаления массы. Так как удаление массы с недеформируемого балансировочного зубца нельзя считать точечным, вместо (4) используем следующее выражение [11]
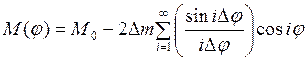 , (6)
, (6)
где ∆φ – угол, под которым зубец виден из центра окружности. В рассматриваемом примере ∆φ = 7,50 и (6) тогда имеет вид:
![]() . (7)
. (7)
Удаление с зубца №1 (его ориентация соответствует φ = 0) массы
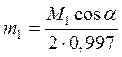
приводит к устранению косинусной составляющей выражения (5). Синусную часть можно представить в виде:
![]()
Максимум неуравновешенной массы при этом расположен под углом φ = 2700. Для устранения этой формы дефекта надо удалить массу с зубца № 19, равную
 .
.
В результате этих операций массовый дефект вида ![]() будет полностью устранен, но одновременно возникнут новые формы массового дефекта, а именно
будет полностью устранен, но одновременно возникнут новые формы массового дефекта, а именно
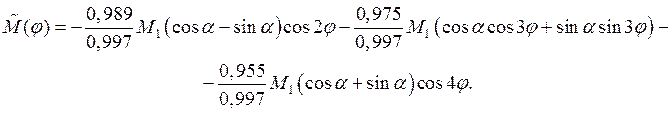
![]() (8)
(8)
Удалим две равные массы с зубцов №7 φ = 900) и № 19 (φ = 2700)
 . (9)
. (9)
Эта процедура устраняет массовый дефект 2-й формы (первое слагаемое в (8)), но образует дополнительный дефект 4-й формы:
–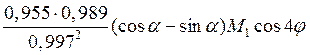 .
.
Суммарный массовый дефект 4-й формы тогда равен
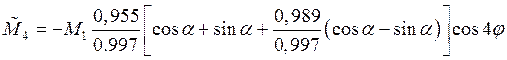 . (10)
. (10)
Этот дефект устраняют удалением четырех равных масс с зубцов № 4, 10, 16 и 22 (соответственно φ = 450, 1350, 2250 и 3150)
 . (11)
. (11)
Осталось удалить 3-ю форму дефекта (второе слагаемое (8)). Это достигают удалением трех одинаковых масс с зубцов № 5, 13, 21, равных
 , (12)
, (12)
а также удалением трех одинаковых масс с зубцов № 3, 11 и 19, равных
 . (13)
. (13)
В итоге получаем схему удаления массового дефекта ![]() , приведенную в таблице 1. Полученные результаты показывают, что процесс балансировки резонатора методом удаления точечных масс оказывается сложным. Основная проблема состоит в удалении строго определенной массы с каждого зубца, что представляет существенную сложность с технической точки зрения.
, приведенную в таблице 1. Полученные результаты показывают, что процесс балансировки резонатора методом удаления точечных масс оказывается сложным. Основная проблема состоит в удалении строго определенной массы с каждого зубца, что представляет существенную сложность с технической точки зрения.
Возможен и другой, более простой вариант балансировки зубчатого резонатора удалением точечных масс. Рассмотрим его также на примере устранения массового дефекта 1-й формы, который описывается (5). Будем удалять массу Мудi с зубцов по закону
![]() , (14)
, (14)
где φi – угловое положение i-го зубца, m – коэффициент.
Таблица 1 – Алгоритм удаления массового дефекта ![]()
Номер зубца | Удаляемая масса |
1 |
|
3 |
|
4 |
|
5 |
|
7 |
|
10 |
|
11 |
|
13 |
|
16 |
|
19 |
|
21 |
|
22 |
|
Очевидно, что при удалении масс с зубцов согласно (14), из начального распределения массы резонатора вычитается распределение
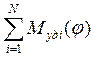 ,
,
где N – количество зубцов.
Чтобы его вычислить, определим массовое распределение Мудi (φ), возникающее при удалении массы Мудi для каждого зубца резонатора. В качестве примера в таблице 2 приведены выражения для Муд i (φ) для 16-зубцового резонатора (разложение ограничено первыми четырьмя членами).
Таблица 2 – Массовое распределение, возникающее при удалении масс с 16-зубцового резонатора
Номер зубца i | Удаляемая масса Мудi | Массовое распределение Мудi (φ) |
1 |
|
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
|
|
14 |
|
|
15 |
|
|
16 |
|
|
Для заданного значения α вычислим по (14) величину удаляемой массы для каждого зубца. В качестве примера в таблице 3 приведены результаты вычисления Мудi для α=1740.
Таблица 3 – Значения удаляемых масс для α = 1740
Номер зубца, i | Угловое положение зубца, φi , град. | Удаляемая масса Муд i = m[1+cos(φi+α)] |
1 | 0 | 0,0055m |
2 | 22,5 | 0,0412m |
3 | 45 | 0,2229m |
4 | 67,5 | 0,5228m |
5 | 90 | 0,8955m |
6 | 112,5 | 1,284m |
7 | 135 | 1,6293m |
8 | 157,5 | 1,8788m |
9 | 180 | 1,9945m |
10 | 202,5 | 1,9588m |
11 | 225 | 1,7771m |
12 | 247,5 | 1,4772m |
13 | 270 | 1,1045m |
14 | 292,5 | 0,716m |
15 | 315 | 0,3707m |
16 | 337,5 | 0,1212m |
Вычислим значения ![]() по формуле
по формуле ![]() , подставим полученные значения
, подставим полученные значения ![]() в распределения
в распределения ![]() , приведенные в таблице 2, и представим их сумму в виде:
, приведенные в таблице 2, и представим их сумму в виде:
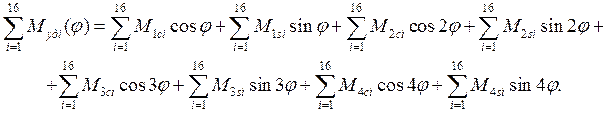 (15)
(15)
Значения множителей в этом выражении равны:
 (16)
(16)
Из (16) следует, что при заданном таблицей 3 алгоритме балансировки, 2-я, 3-я и 4-я формы массовых дефектов не образуются. Для устранения имеющейся 1-й формы массового дефекта надо выбрать m так, чтобы множители
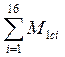 и
и 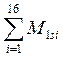
компенсировали соответствующие множители в (5), то есть
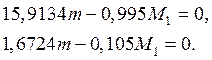 (17)
(17)
Для нахождения коэффициента mможно пользоваться любым из этих двух уравнений, получаем: m=0,0625M1. Подставляя это значение в правый столбец таблицы 3, вычисляем значения удаляемой массы для каждого зубца. Аналогичным образом могут быть удалены и другие формы массового дефекта. Общая формула для массы, удаляемой с каждого зубца резонатора, при балансировке k-формы массового дефекта предложенным алгоритмом имеет вид
![]() , (18)
, (18)
где Mk и φ0k– параметры массового дефекта k-й формы, φi– угловое положение i-го зубца.
На рисунке 6 приведены диаграммы, иллюстрирующие удаление одной и той же 1-й гармоники массового дефекта (в долях от М1) с 24-зубцового резонатора обоими алгоритмами.


а б
Рисунок 6 – Распределение удаляемой массы по зубцам при устранении 1-й формы массового дефекта (α=100) двумя балансировочными алгоритмами:
а – алгоритм [9]; б – предложенный алгоритм
Выводы
Сравнение результатов расчета показывает, что при использовании предложенного в работе алгоритма общая удаляемая масса гораздо меньше, чем при использовании алгоритма [9], причем максимальное значение удаляемой массы меньше почти в 6 раз. Поскольку при электрохимическом удалении неуравновешенная масса удаляется одновременно со всех зубцов, то общее время обработки определяется временем удаления максимальной массы. В результате время балансировочного процесса сокращается в разы, благодаря чему предложенный балансировочный алгоритм оказывается гораздо более удобным для практической реализации.
Данный алгоритм балансировки имеет и другие преимущества:
- может быть использован при любом числе зубцов на кромке резонатора;
- не требует выполнения сложных расчетов при определении масс, удаляемых с зубцов;
- не создает более высоких форм массового дефекта, поэтому может быть успешно использован как при одновременном удалении всех форм массового дефекта, так и при их поочередном удалении;
- удаляемая масса распределяется по зубцам более равномерно.
Разработанный электрохимический метод балансировки прост в технической реализации, не требует дорогостоящего оборудования и легко поддается автоматизации.
Список литературы
1. Leger P. QUAPASON – a New Low-cost Vibrating Gyroscope // Proc. 3rd International Conference on Integrated Navigation Systems. (St.-Petersburg, May 28-29 1996). Saint-Petersburg, 1996. Part I. P. 143‑150.
2. Chikovani V.V., Yatsenko Yu.A. Investigation of Azimuth Accuracy Measurement with Metallic Resonator Coriolis Vibratory Gyroscope // Proc. of XVII International Conference on Integrated Navigation Systems. (St.-Petersburg, 31 May - 2 June 2010). St.-Petersburg: "ElektroPribor", 2010. P. 25-30.
3. Lynch D.D. Vibration-induced drift in the hemispherical resonator gyro // Proc. Annual Meeting of the Institute of Navigation. 23-25 June, 1987. Dayton, Ohio, 1987. P. 34-37.
4. Бодунов Б.П., Лопатин В.М., Лунин Б.С. Способ балансировки полусферического резонатора волнового твердотельного гироскопа : пат. 2147117 РФ. 1998.
5. Белкин А.А. Разработка технологии и оборудования для балансировки полусферического резонатора волнового твердотельного гироскопа лазерным излучением : дис. … канд. техн. наук. М., 2000.
6. Loper E.J., Lynch D.D. Vibratory rotational sensor : пат. EU 0141621 A2. 1984.
7. Лунин Б.С., Торбин С.Н., Лещев В.Т., Чуманкин Е.А. Способ балансировки металлического зубчатого резонатора волнового твердотельного гироскопа : заявка на пат. 2013103755 РФ. 2013.
8. Розбери Ф. Справочник по вакуумной технике и технологии : пер. с англ. М.: Энергия, 1972. 456 с.
9. Жбанов Ю.К., Журавлев В.Ф. О балансировке волнового твердотельного гироскопа // Известия РАН. Сер. Механика твердого тела. 1998. № 4. С. 4‑16.
10. Матвеев В.А., Липатников В.И., Алехин А.В. Проектирование волнового твердотельного гироскопа. М.: Изд-во МГТУ им. Н.Э. Баумана, 1997. 168 с.
11. Никольский С.М. Курс математического анализа. Т. 2. М.: Наука, 1991. 543 с.
Публикации с ключевыми словами: балансировка, бесплатформенная инерциальная навигационная система, волновой твердотельный гироскоп, цилиндрический резонатор
Публикации со словами: балансировка, бесплатформенная инерциальная навигационная система, волновой твердотельный гироскоп, цилиндрический резонатор
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||

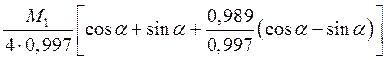


 +
+