научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 04, апрель 2013
DOI: 10.7463/0413.0574259
УДК: 629.7.05
ОАО «РКК «Энергия» им. С.П. Королева»
Введение
Дальнейшее развитие пилотируемой космонавтики, связанное с продолжением эксплуатации Международной космической станции (МКС) и межпланетными полетами подразумевает многократное выполнение операций сближения и стыковки космических аппаратов (КА), для осуществления которых необходимо решить задачу обнаружения и измерения координат пассивного КА бортовыми средствами активного КА.
Обнаружение и измерение координат пассивного КА производится посредством штатной радиотехнической аппаратуры (на КА «Союз» и «Прогресс») и лазерных локационных систем (ЛЛС), используемых на перспективных КА. К настоящему времени известен ряд ЛЛС, предназначенных для управления сближением и стыковкой КА[1-6], часть из которых прошла летные испытания на борту КА SpaceShuttle (NASA) [5], КА ATV (ESA) [6] и др. Однако образцы, прошедшие летные испытания имеют ограниченную дальность (0,3…3,0 км), и ряд других недостатков.
В связи с использованием более совершенной элементной базы, необходимостью увеличения дальности ЛЛС до 5 км и более, при снижении баллистических ограничений на положение небесных тел относительно пассивного КА, а также ужесточением требований лазерной безопасности, процесс разработки бортовых ЛЛС для перспективных КА усложняется. На практике оказывается, что использование уже известных и проверенных инженерных методов [7] оказывается весьма трудоемким и затратным, так как отсутствуют специализированные средства для разработки ЛЛС на основе современных информационных технологий (например, системы автоматизированного проектирования).
Научная новизна состоит в том, что в ходе оптимизации параметров ЛЛС найдено множество Парето-оптимальных решений по группе критериев максимальной дальности и безопасности излучения, из которых разработчик может выбирать наиболее приемлемые для технической реализации и обеспечения требуемых техническим заданием характеристик ЛЛС.
1 Особенности бортовых ЛЛС КА
Реализация бортовых ЛЛС КА может осуществляться в двух основных вариантах: лазерных дальномерах и лазерных локаторах, еще называемых лидарами (англ. lidar: lightdetectionandranging) или ладарами (англ. ladar: laserdetectionandranging), использующих узкие коллимированные пучки зондирующего излучения, для наведения которых обычно используется оптико-механический сканер.
Последнее десятилетие интенсивно развивается технология 3D Flash Ladar, позволяющая отказаться от сканирования (например, ЛЛС, описанная в [5]). Серьезным недостатком технологии 3DFlashLadar является падение плотности излучения в пучке подсветки с дальностью измерений, деление принятого сигнала на большое количество элементов матричного фотоприемника и ограниченное разрешение. Разработка бортовой ЛЛС на основе 3DFlashLadar, обеспечивающей измерения в диапазоне дальностей от единиц метров до нескольких километров требует нахождения нетривиальных конструкторских решений и дальнейшего усовершенствования элементной базы.
Для улучшения характеристик обнаружения пассивного КА на нем могут размещаться ответные оптические устройства. В настоящее время наиболее предпочтительным выглядит использование пассивных ответных устройств – уголковых отражателей (УО).
При использовании бортовых ЛЛС для управления сближением пилотируемых КА необходимо учитывать требования лазерной безопасности для защиты органов зрения экипажа. Источниками зондирующего излучения для указанных ЛЛС преимущественно являются твердотельные лазеры с полупроводниковой накачкой или волоконные лазеры, генерирующие излучение на длинах волн λ = 1,06 мкм и λ = 1,5 мкм, для которых безопасные величины энергии импульсов отличаются на три порядка.
2 Оценка характеристик ЛЛС
Для определения характеристик ЛЛС выполняются светотехнические расчеты, основанные на приближениях геометрической оптики, которые сводятся к «классическому» уравнению лазерной локации [7, 8, 9], изменяющему свою форму в зависимости от дальности до объекта и наличия на нем ответных устройств.
Основное допущение состоит в следующем. Диаграмма подсветки принимается в виде конуса с плоским углом γ при вершине
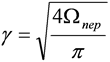 , (1)
, (1)
в котором равномерно распределено зондирующее излучение. Аналогично, отраженное излучение также считается равномерно распределенным в телесном угле Ωотр, внутри которого находится приемная апертура.
Лазерный источник с мощностью излучения Рл, излучающий через оптическую систему с пропусканием τпер, создает зондирующий пучок с энергетической силой света
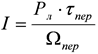 . (2)
. (2)
На расстоянии D будет создаваться энергетическая освещенность
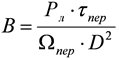 . (3)
. (3)
Объект с площадью Sоб и коэффициентом отражения ρоб, подсвечиваемый зондирующим пучком, будет иметь энергетическую силу света
 , (4)
, (4)
где Ωотр – телесный угол распространения отраженного объектом излучения, определяемый характеристиками его поверхности.
При работе по объекту, диффузно рассеивающему излучение подсветки, предполагается, что его поверхность отражает излучение по закону Ламберта
Р(ψ) = Р0 ∙cos (ψ), (5)
где Р0 – мощность пучка подсветки, падающего на отражающую поверхность; ψ – угол относительно нормали к отражающей поверхности.
Далее, при оценке работы ЛЛС по диффузно отражающей поверхности производится ее экстраполяция ламбертовской поверхностью.
В этом случае энергетическая сила света объекта будет равна
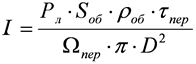 . (6)
. (6)
В плоскости ЛЛС отраженным от объекта излучением будет создаваться энергетическая освещенность
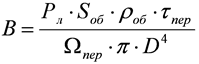 . (7)
. (7)
Приемный объектив диаметром dпр будет собирать мощность отраженного сигнала, равную
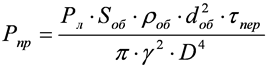 . (8)
. (8)
С учетом пропускания приемного тракта τпр на фотоприемное устройство (ФПУ) будет поступать мощность
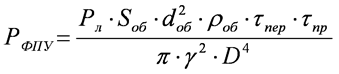 . (9)
. (9)
откуда дальность ЛЛС при работе по точечному диффузному объекту равна
 , (10)
, (10)
где: Рmin – минимальная мощность принимаемого сигнала, определяемая следующим соотношением:
Рmin = q∙Рпор, (11)
где: q – отношение сигнал шум; Рпор – пороговая мощность сигнала, регистрируемая ФПУ.
Пороговую мощность сигнала можно определить как наименьшую мощность излучения, которая может быть обнаружена данным ФПУ [10]. С учетом полосы частот ее также можно определить как среднеквадратическое значение действующего на ФПУ синусоидально-модулированного потока излучения, при котором среднеквадратическое значение принимаемого сигнала равно среднеквадратическому значению шума в заданной полосе частот [10].
Если диаметр зондирующего пучка равен или меньше площади объекта, то тогда
 , (12)
, (12)
и
 . (13)
. (13)
Если на объекте установлен УО с площадью SУО, коэффициентом отражения ρУО и телесным углом распространения отраженного пучка ΩУО, то дальность ЛЛС определяется выражением
 . (14)
. (14)
Выражение (14) позволяет выполнить оценки при ряде допущений:
- подразумевается, что УО полностью покрывается зондирующим пучком;
- не учитывается дифракционная расходимость;
- не учитывается зависимость SУО и ρУО от угла между нормалью к входной грани УО и направлением на него.
Однако точности выражения (14) вполне достаточно для инженерных расчетов характеристик ЛЛС. Соотношения (2)-(14) остаются справедливы и при замене мощности сигнала Р на энергию Е.
Применение ЛЛС для обнаружения космических объектов ограничивается внешними помехами (засветками). В оптическом диапазоне имеется мощнейший источник помех – Солнце. Однако, вероятность попадания в поле зрения ЛЛС солнечного диска очень низка (~ 10–5) из-за его малого углового размера.
В орбитальном полете более высока вероятность фоновой засветки ЛЛС от освещенной поверхности планеты. Часть излучения Солнца отражается от подстилающей поверхности, а еще одна часть рассеивается в атмосфере. Однако с точки зрения бортовой ЛЛС помеху создает только излучение, попадающее в приемную апертуру, в не зависимости, от того, отраженное оно от поверхности или рассеянное в атмосфере. На практике для оценки мощности фоновой засветки берется интегральное монохроматическое альбедо планеты, освещаемой Солнцем, при этом не учитывается, отражается излучение Солнца от подстилающей поверхности или рассеивается в атмосфере.
Излучение Солнца характеризуется спектральной плотностью потока энергии, проходящего через единицу поверхности в окрестности планеты, рассчитанным на единичный интервал длин волн Fλ. Для подавления засветки в ЛЛС применяется спектральная селекция, для чего используются интерференционные фильтры с шириной полосы пропускания Δλ (предполагается, что ее центральная длина волны совпадает с длиной волны генерации лазера).
Фоновую засветку создает некоторая часть подстилающей поверхности с альбедо ρп, имеющая площадь Sп, которая попадает в поле зрения ЛЛС. При аппроксимации подстилающей поверхности ламбертовским отражателем на приемном объективе ЛЛС будет создаваться энергетическая освещенность
 , (15)
, (15)
где h – дальность до подстилающей поверхности. Так как
 , (16)
, (16)
то мощность фонового сигнала, поступающего через объектив с площадью приемной оптики Sпр и пропусканием τпр составляет
 . (17)
. (17)
Для определения фоновой засветки среднее значение Fλ умножается на ширину полосы пропускания Δλ. При этом не учитываются отклонения Fλ по спектру от среднего значения, в результате чего в оценку засветки вносится погрешность, возрастающая с увеличением полосы пропускания. В [11,12] указаны значения Fλ для определенных длин волн (например, 0,8 мкм, 0,9 мкм, 1,0 мкм), которые не всегда совпадают с длиной волны генерации лазера, используемого в ЛЛС.
Распределение энергии в спектре Солнца в первом приближении соответствует распределению в спектре излучения абсолютно черного тела (АЧТ) с эффективной температурой Т = 6000 К [12]. Таким образом, спектральное распределение мощности излучения Солнца, испускаемой единицей поверхности, можно определить по закону Планка
 , (18)
, (18)
где h = 6,63∙10-34 Дж∙с – постоянная Планка; c = 3∙108 м/с – скорость света в вакууме; λ –длина волны излучения; k = 1,38∙10-23 Дж/К – постоянная Больцмана; T – абсолютная температура.
Плотность потока энергии излучения Солнца на 1 нм вычисляется по выражению
 , (19)
, (19)
где Ωс = 6,8∙10–5 ср – телесный угол, в котором наблюдается Солнце с Земли; Sc = 6,09∙1018 м2 – площадь поверхности Солнца.
Таким образом, выражение для оценки фоновой засветки будет иметь вид
 . (20)
. (20)
Для выполнения целевых задач мощность излучения ЛЛС не должна быть ниже порогового уровня, определяемого отношением сигнал/шум q (см. выражение (11)).
Основными источниками шума в ФПУ ЛЛС являются темновой шум и фоновый шум, а результирующая величина эквивалентной мощности шума тогда определяется выражением [9]
![]() . (21)
. (21)
Мощность темнового сигнала Рт зависит от типа и режима работы ФПУ. Если принять, что темновой сигнал РТ значительно меньше сигнала от фона Рфз, то
Рш ≈ Рфз.
Тогда, при наличии фоновой засветки минимальное значение принимаемой энергии составит
Emin = q∙Рфз∙tи, (22)
где tи – длительность зондирующего импульса.
Энергетика подсветки ЛЛС должна обеспечивать устойчивость к внешним помехам, но при этом ее максимальные значения ограничиваются требованиями лазерной безопасности.
Энергия излучения, проходящая через ограничивающую апертуру (зрачок наблюдателя)
 , (23)
, (23)
где Ез = Ел∙τпер – энергия зондирующего пучка; dз – диаметр зрачка наблюдателя.
Безопасная энергия импульсов зондирующего излучения рассчитывается по соотношению
 , (24)
, (24)
где ЕДПИ – допустимые пределы излучения (ДПИ) зондирующего импульса согласно нормативам лазерной безопасности.
Отсюда дальность безопасного наблюдения зондирующего пучка
 . (25)
. (25)
Авторами была разработана программа «МИТРА», предназначенная для оценки возможностей бортовых ЛЛС КА при работе по близкорасположенным или удаленным космическим объектам, имеющим диффузно рассеивающую поверхность, а также снабженными УО. Оценка параметров ЛЛС выполняется как при отсутствии световых помех, так и с учетом фоновой засветки от подстилающей поверхности. Для вычислений используется описанный выше математический аппарат. Программа также позволяет рассчитать параметры ЛЛС, обеспечивающие безопасность для органов зрения при случайном облучении в спектральном диапазоне 0,81…1,5 мкм согласно требованиям, устанавливаемым ГОСТ Р 50723-94. Программа зарегистрирована в реестре ФИПС (свидетельство о государственной регистрации № 2013610537).
Результаты выполненного с помощью программы «МИТРА» моделирования показывают, что применение УО позволяет обеспечить дальность измерений ЛЛС в диапазоне 20…55 км без превышения зондирующими импульсами ДПИ, заданных нормами лазерной безопасности. Работа по диффузно отраженному сигналу, с использованием длины волны зондирующего излучения λ = 1,06 мкм с низким значением ДПИ (ЕДПИ = 2·10–6 Дж, согласно ГОСТ Р 50723-94) является наиболее сложной задачей, требующей согласования параметров ЛЛС и требований безопасности.
Максимальной эффективности по одному критерию соответствует одни значения конструктивных параметров, по следующему критерию – другие, поэтому необходимо найти значения параметров ЛЛС, которые могут существенно отличаться при оценке по различным критериям. Следовательно, для реализации ЛЛС с характеристиками, одновременно удовлетворяющих требованиям по назначению и требованиям лазерной безопасности, необходимо решение задачи многокритериальной оптимизации.
3 Решение задачи оптимизации параметров ЛЛС
Максимальная дальность ЛЛС – одно из основных требований по назначению, которое задается в техническом задании на разработку. Дальность измерений определяется точностями предварительного наведения при сближении КА, обеспечиваемой баллистическими методами, инерциальной навигацией и внешним целеуказанием. При использовании ЛЛС для управления сближением пилотируемых КА также вводятся требования по безопасности зондирующего излучения.
Таким образом, при оценке характеристик ЛЛС эти два показателя играют наиболее существенную роль.
Цель оптимизации ЛЛС формулируется как достижение максимальной дальности локации пассивного КА по диффузно отраженному сигналу при минимальной дистанции безопасного наблюдения зондирующего пучка с длиной волны лазерного излучения λ = 1,06 мкм.
Для построения целевой функции в качестве показателей используются выражения (10) и (25)
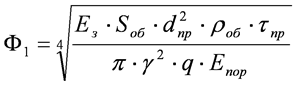 , (26)
, (26)
 . (27)
. (27)
Оптимизируемые параметры, с одной стороны должны принимать значения, отличающиеся не менее чем в несколько раз, что позволяет разработчику их варьировать, а с другой оказывать существенное влияние на показатели. Параметры бортовой ЛЛС КА в силу конструктивных ограничений находится в пределах, указанных в таблице 3.1.
Таблица 3.1 – Диапазон параметров бортовой ЛЛС
Параметр | Значение |
Ез, мДж | 0,4…30 |
dпр, см | 1…10 |
τпр | 0,1…0,9 |
γ, мрад | 0,6…6 |
q | 3…10 |
Соответствующие значения пороговой энергии ФПУ и ДПИ составляют: Епор = 6·10–16 Дж (ФУО-119-02.01 производства ФГУП «НПО «Орион»), ЕДПИ = 2·10–6 Дж при диаметре ограничивающей апертуры dА = 7 мм. Для оценки рассматривался объект с диффузно отражающим корпусом, имеющий следующие параметры: Sоб = 3,14 м2; ρоб = 0,5. Параметры ЛЛС: dпр = 5 см; τпр = 0,5; q = 10.
Дальность ЛЛС и дистанция безопасного наблюдения в первую очередь определяются энергией импульса и расходимостью зондирующего пучка. Если их принять в качестве оптимизируемых параметров, то задача сводится к поиску экстремума функции двух переменных: Ез и γ. Эти два параметра образуют замкнутое и ограниченное подмножество двумерного пространства, то есть компакт, на котором эти величины имеют только положительные значения.
При скалярной постановке задачи наиболее простой путь формирования целевой функции заключается в линейной свертке отдельных критериев в один, однако, исходя из противоречивого характера критериев для максимальной дальности ЛЛС и дистанции безопасного наблюдения, представляет проблему окончательный выбор весовых коэффициентов.
Практически применимым является метод комплексного критерия (отношение двух показателей, один из которых необходимо максимизировать, а второй – минимизировать).
 . (28)
. (28)
При использовании комплексного критерия целевая функция будет иметь вид
 . (29)
. (29)
Анализ выражения (29) показывает, что целевая функция непрерывна на рассматриваемом компакте (при данных значениях Ез и γ). Частные производные целевой функции равны
 , (30)
, (30)
 . (31)
. (31)
Как видно из выражений (30)-(31), частные производные не равны нулю в рассматриваемом диапазоне значений Ез и γ, то есть в данном компакте отсутствуют стационарные точки. Так как функция непрерывна на данном компакте, то она должна обязательно иметь в нем наибольшее и наименьшее значения, как следует из второй теоремы Вейерштрасса [13].
Для дальнейшего исследования целевой функции использовалось расширение Optimization Toolbox, входящее в состав математического пакета MATLAB Version 7.6.0.324 (R2008a). Для решения задачи оптимизации применялся алгоритм последовательного квадратичного программирования (SQP – англ. sequential quadratic programming), представляющий собой разновидность квазиньютоновского метода. На сегодняшний день методы SQP входят в число наиболее эффективных оптимизационных методов общего назначения [14].
Область поиска задавалась в виде прямоугольника путем указания минимального и максимального значений каждого параметра. Использовалась стандартная функция «fmincon», осуществляющая поиск максимума скалярной функции многих переменных при наличии ограничений.
Максимальное значение целевой функции соответствует значениям оптимизируемых параметров Ез = 0,4 мДж и γ = 6,0 мрад, находящихся на границе компакта. Поиск минимума целевой функции также дает значения параметров на границе компакта: Ез = 30,0 мДж и γ = 0,6 мрад.
В таблице 3.2 представлены значения оптимизируемых параметров, значения целевой функции в данных точках и соответствующие значения показателей.
Таблица 3.2 – Значения целевой функции R, показателей и оптимизируемых параметров ЛЛС
Величина целевой функции | Значение | Значения оптимизируемых параметров | Значения показателей | ||
Ел, мДж | γ, мрад | Ф1, км | Ф2, м | ||
Максимальная | 49,99 | 0,4 | 6,0 | 1,30 | 26,10 |
Минимальная | 6,75 | 30,0 | 0,6 | 9,65 | 1429,10 |
На рис. 3.1 представлен график целевой функции R.
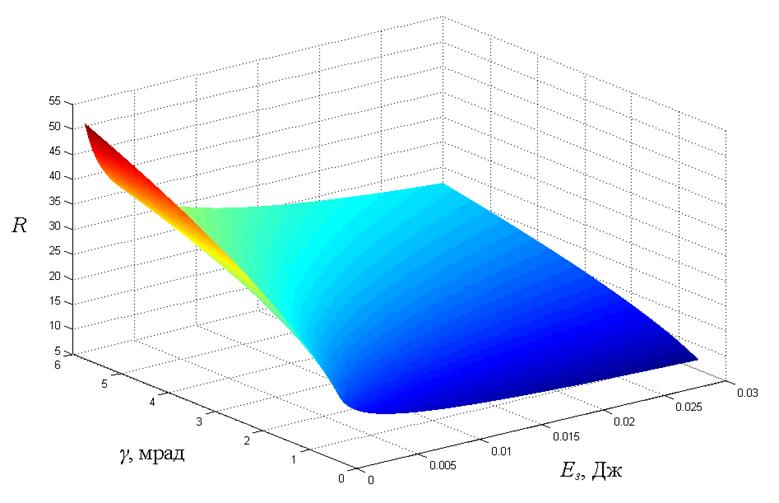
Рисунок 3.1 – График целевой функции R для ЛЛС, работающей по диффузно отраженному сигналу на длине волны λ = 1,06 мкм
Таким образом, максимальная величина отношения двух показателей достигается при минимальной энергии импульса и максимальной расходимости зондирующего пучка, а минимальной дистанции безопасного наблюдения соответствует минимальная дальность ЛЛС.
Из данных, полученных методами математического моделирования, следует, что не представляется возможным найти решение данной задачи оптимизации параметров ЛЛС в виде экстремума целевой функции. Использование комплексного критерия позволяет определить значения оптимизируемых параметров, соответствующие максимальной или минимальной величине целевой функции.
Результаты такой оптимизации не всегда применимы на практике, а их использование разработчиком затруднительно.
В ходе решения реальных задач разработчику нередко приходится идти на компромисс, отклоняясь от экстремальных значений показателей, чтобы удовлетворить требованиям по назначению, которые задаются в техническом задании на разработку. При этом на практике удобно рассматривать совокупность решений, для которых улучшение значения одного критерия приводит к увеличению значения второго.
На принципе компромисса основана векторная постановка задачи, когда может быть использован метод Парето, позволяющий выделить множество решений, где уменьшение значения одного критерия приводит к увеличению значений других критериев.
Если для некоторой пары возможных решений имеет место неравенство [15]
Фi (х**) ≥ Фi (х*), (32)
то первое решение будет предпочтительнее второго (если выполняется максимизация Фi), а второе решение ни при каких обстоятельствах не может оказаться выбранным и его можно исключить из последующего процесса принятия решений. Исключение всех подобного рода решений приводит к множеству Парето [15]
Р(Х) = {х″ ∈ Х| не существует такого х′ ∈ Х, что Фi (х′) ≥ Фi (х″)}. (33)
При необходимости выбора единственной альтернативы следует ввести новые критерии и ограничения, либо использовать экспертные оценки.
Роль множества Парето при решении задач многокритериальной оптимизации определяется следующей теоремой. Если для некоторых весовых коэффициентов μi, i ∈ [1, k] и вектора х* ∈ Dх имеет место равенство
 , (34)
, (34)
то вектор х* оптимален по Парето.
Теорема показывает, что выбор определенной точки из множества Парето эквивалентен указанию весов для каждого из частных критериев оптимальности, определение которых затрудняет использование на практике линейную свертку отдельных критериев в один (окончательный выбор коэффициентов μi).
Проверить неулучшаемость альтернатив множества Парето для непрерывной области критериев возможно геометрически [15]. На практике данный прием называют «обход конусом».
Использование метода Парето в отличие от скалярной постановки задачи позволяет избежать неопределенности при выборе значимости критериев оценки. Возможен сразу выбор наиболее приемлемого сочетания критериев исходя из имеющихся у разработчика ресурсов.
Для получения множества альтернативных решений используются зависимые друг от друга показатели. При оптимизации ЛЛС в показателях Ф1 и Ф2 присутствует отношение Ез/γ2, которое обеспечивает связь между дальностью ЛЛС и безопасной дистанцией наблюдения.
Множество Парето, определяемое показателями Ф1 и Ф2 для одинаковых значений Ез/γ2, представлено в виде кривой на рис. 3.2.
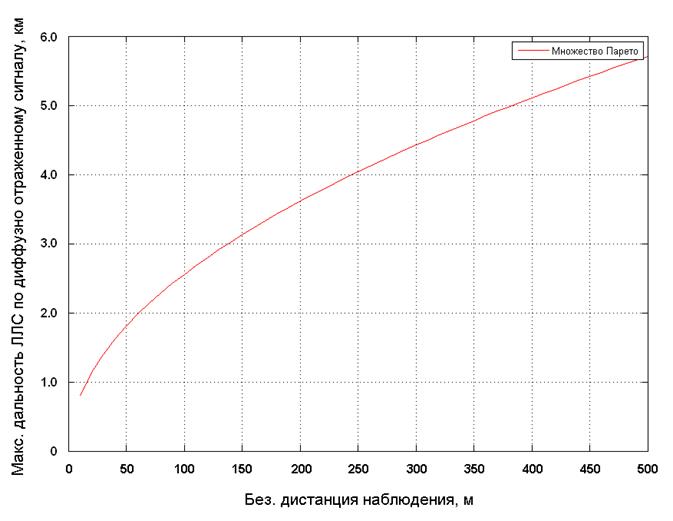
Рисунок 3.2 – Множество Парето для работы ЛЛС по диффузно отраженному сигналу на длине волны λ = 1,06 мкм
Обход конусом графика на рис. 3.2 указывает принадлежность полученной кривой к множеству Парето. Анализ полученной кривой показывает, что при дальности ЛЛС 5 км безопасная дистанция наблюдения составляет 390 м. Если безопасность излучения обеспечивается на дистанции 50 м, то дальность ЛЛС снижается до 1,61 км. Полученные значения подтверждаются данными моделирования с использованием программы «МИТРА».
Представленный на рис. 3.2 график позволяет разработчику выбрать наиболее приемлемое для конкретного случая соотношение между дальностью ЛЛС и дистанцией безопасного наблюдения.
Безопасность в полете может обеспечиваться ограничением диапазона дальностей работы ЛЛС (когда ЛЛС не используется ближе некоторой дистанции) с блокировкой излучения при уменьшении допустимого расстояния. Также в ЛЛС могут быть использованы несколько каналов с разной мощностью излучения для разных дистанций. Для обеспечения надежности измерений, дальности устойчивой работы разных каналов ЛЛС и других средств измерения координат пассивного КА должны обеспечивать как можно большее перекрытие. Здесь неоценимую помощь разработчику окажут подобные графики, позволяющие подобрать подходящее значение показателей, определяемое параметрами ЛЛС.
Заключение
Решена задача Парето-оптимизации параметров бортовых ЛЛС, используемых для управления сближением и стыковкой КА по критериям максимальной дальности и дистанции безопасного наблюдения. Использование множеств Парето позволяет разработчику аппаратуры выбирать наиболее приемлемые с точки зрения технической реализации решения, обеспечивающие требуемые техническим заданием характеристики ЛЛС.
В результате Парето-оптимизации получены дальности ЛЛС в диапазоне от 1,61 до 5 км и соответствующие им значения безопасной дистанции наблюдения в диапазоне от 50 м до 390 м, что позволяет решить задачу применения ЛЛС с длиной волны зондирующего излучения λ = 1,06 мкм для управления сближением КА в этом диапазоне расстояний при выполнении требований лазерной безопасности.
Авторы выражают свою благодарность д.т.н. Н.Е. Зубову за помощь при работе над материалом для данной статьи.
Список литературы
1. Lehr C.G. Laser Tracking Systems. Vol. 2. Laser Applications. Academic Press, 1974.
2. Lowrey D.O., Adelman S. A 10,6 micron radar for space rendezvous and docking // Wescon. Profess. Progr. 1975. Vol. 19. S-1. P. 9.1/1–9.1/7.
3. Flom T. Spaceborne laser radar // Appl. Opt. 1972. Vol. 11, no. 2. P. 291.
4. Федосеев В.И. Автоматическая лазерная система контроля параметров сближения кооперируемых космических аппаратов // Оптический журнал. 1996. № 7. С. 66-70.
5. Christian J.A., Hinkel H., D’Souza C.N., Mauire S., Patangan M. The Sensor Test for Orion RelNav Risk Mitigation (STORRM) Development Test Objective. Режим доступа: http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20110013437_2011014090.pdf (дата обращения 29.01.2012).
6. The GNG measurement system for the automated transfer vehicle. Режим доступа: http://www.issfd.org/ISSFD_2004/papers/P1010.pdf (дата обращения 14.01.2012).
7. Малашин М.С., Каминский Р.П., Борисов Ю.Б. Основы проектирования лазерных локационных систем. М.: Высшая школа, 1983. 207 с.
8. Лазерная дальнометрия / Л.А. Аспис, В.П. Васильев, В.Б. Волконский и др.; под ред. В.П. Васильева и Х.В. Хинрикус. М.: Радио и связь, 1995. 256 с.
9. Назаров В.Н., Балашов И.Ф. Энергетическая оценка импульсных лазерных дальномеров. СПбГУИТМО, 2002. 38 с. Режим доступа: http://de.ifmo.ru/bk_netra/start.php?bn=27 (дата обращения 19.01.2012).
10. Мирошников М.М. Теоретические основы оптико-электронных приборов. СПб.: Лань, 2010. 704 с.
11. Аллен К.У. Астрофизические величины : пер. с англ. М.: Мир, 1977. 448 с.
12. Основы импульсной лазерной локации: учеб. пособие для вузов / В.И. Козинцев, М.Л. Белов, В.М. Орлов и др.; под ред. В.Н. Рождествина. М.: Изд-во МГТУ им. Н.Э. Баумана, 2010. 571 с.
13. Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ: учеб. Ч. 1 / под ред. А.Н. Тихонова. 3-е изд., перераб. и доп. М.: ТК Велби, Изд-во Проспект, 2006. 672 с.
14. Измаилов А.Ф., Солодов М.В. Численные методы оптимизации: учеб. пособие. М.: ФИЗМАТЛИТ, 2005. 304 с.
15. Ногин В.Д. Принятие решений в многокритериальной среде: количественный подход. 2-е изд., испр. и доп. М.: ФИЗМАТЛИТ, 2004. 176 с.
Публикации с ключевыми словами: моделирование, разработка, оптимизация, космический аппарат, лазерная локационная система
Публикации со словами: моделирование, разработка, оптимизация, космический аппарат, лазерная локационная система
Смотри также:
- 77-48211/654681 Исторические аспекты развития и принципы построения бортовых лазерных локационных систем для сближения и стыковки космических аппаратов
- Автоматизированные экспертные системы. Применение в медицине
- 77-30569/345396 Исследование свойств квазиоптимального и оптимального алгоритмов переориентации космического аппарата
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



