научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#2 февраль 2006
А
А. Б. Барский, д-р техн. наук, проф., МГУПС;
В. В. Шилов, канд. техн. наук, проф., "МАТИ"—РГТУ им. К. Э. Циолковского
SPMD-архитектура и параллельная обработка структур данных
Обсуждается подход к параллельной обработке структур данных, основанных на ссылках. Приводятся примеры его программной реализации применительно к предложенной авторами архитектуре многопроцессорной локально-асинхронной вычислительной системы.
Введение
Одним из наиболее часто используемых способов организации информации в памяти ЭВМ является ее представление в виде списков. Списки позволяют достаточно просто отображать данные самой разнообразной природы: произвольные множества, деревья, графы, строки и т. д. Поэтому списки — весьма удобный для программиста способ решать проблемы представления и обработки данных с нестандартной или нерегулярной структурой. Особое значение представление в виде списков приобретает тогда, когда становятся неприменимыми простейшие методы использования памяти.
Основой обработки списков являются [1]:
· озможность оперировать не самими величинами, а их адресами. Это облегчает программирование, экономит память и сокращает затраты на пересылку информации;
· использование цепочки элементов, связанных между собой таким образом, что каждому элементу известен адрес следующего элемента цепочки;
· возможность в качестве значения элемента цепочки иметь как объект простой природы (например числовую или символьную константу), так и адрес начального элемента другой, произвольно сложной цепочки.
Основные операции над списками [2]:
· получение доступа к произвольному элементу списка для анализа и/или изменения содержимого его полей;
· включение нового элемента в заданное место списка или его исключение;
· объединение нескольких списков в один или разбиение списка на несколько;
· копирование списка;
· определение числа элементов в списке;
· сортировка элементов списка по содержимому некоторого поля;
· поиск в списке элемента с заданным значением в некотором поле.
Простота реализации этих операций является одним из наиболее привлекательных свойств списковой организации информации. Однако традиционное представление списков на основе последовательности ссылок предполагает и последовательную обработку их элементов. Все известные алгоритмы, реализующие операции над списками, являются последовательными и ориентированы на однопроцессорные ЭВМ фон-неймановской архитектуры.
Очевидно, что эффективная реализация операций над списками для ЭВМ с параллельной архитектурой представляет достаточно непростую задачу. Например, в работе [3] делается вывод о том, что для наиболее распространенных способов организации и обработки списков на векторно-конвейерных ЭВМ не удается эффективно векторизовать соответствующие алгоритмы выполнения основных операций над списками. Особый интерес представляла бы разработка таких алгоритмов для вычислительных систем (ВС) с большим числом процессорных элементов, например потоковых ВС или ВС с архитектурой "гиперкуб". Вероятно, одной из первых работ в этой области была [4], в которой рассмотрены параллельные алгоритмы реализации некоторых операций над списками и приведены оценки времени их выполнения.
В настоящей статье кратко описывается архитектура многопроцессорной локально-асинхронной ВС [5], обсуждается подход к параллельной обработке списков, предлагаются параллельные алгоритмы выполнения некоторых операций над списками и приводятся соответствующие программы.
Монопрограммная локально-асинхронная ВС
При выборе архитектуры высокопараллельной ВС, состоящей из большого числа одновременно и независимо работающих на общей памяти процессоров, следует учесть, что простота и универсальность многих алгоритмов обработки информации позволяют часто организовать вычислительный процесс таким образом, что каждый процессор может выполнять в целом совершенно идентичные алгоритмы. Это основано на преимущественной обработке больших массивов информации, что позволяет формировать для всех процессоров единственную программу — монопрограмму и выполнять на каждом процессоре ее копию. Разумеется, при этом должны быть предусмотрены механизмы обработки при необходимости на разных процессорах разных элементов однотипных данных, синхронизации обработки общих данных, взаимодействия реализуемых процессов (примеры монопрограмм, построенных с учетом этих требований, можно найти в [5]). Такие ВС будем называть локально-асинхронными. Структура локально-асинхронной ВС представлена на рис. 1.

Рис. 1. Структура локально-асинхронной ВС
Программа располагается в памяти команд, откуда фрагментами считывается в буферы команд БКi процессоров Пi, i = 0,1,…,N - 1. Процессор может представлять собой микропроцессор или процессор RISC-архитектуры. Каждый процессор обладает памятью для хранения стеков вычислительного процесса, модификаторов, дескрипторов массивов, локальных данных. Через коммутатор процессоры связаны с оперативной памятью данных. В состав системы входит синхронизатор, обеспечивающий одновременность начала действий всех процессоров по специальной команде. Отдельно выделенная память — семафоры — предназначена для хранения значений примитивов синхронизации — семафоров и операций над ними.
Алгоритмы параллельной обработки списков
Все дальнейшее изложение будем вести применительно к линейным однонаправленным спискам. Под списком L будем понимать совокупность объектов вида:
ln = (V, C),
где V — ссылка на данные; C — ссылка на некоторый (следующий) элемент этого же списка.
Считаем, что элементы каждой двойки (V, С) расположены в памяти так, что адрес любого элемента определяется прибавлением фиксированного смещения к некоторому базовому адресу. Таким образом, совокупность этих двоек можно рассматривать как массив R — образ списка, в котором места расположения всех элементов заранее известны или могут быть рассчитаны (отметим, что так определенный образ списка аналогичен вектору информации [1], используемому для обеспечения доступа к элементам списка в произвольном порядке). Последний элемент списка (и каждого подсписка) имеет значение C = nil, т. е. ссылается на пустой элемент.
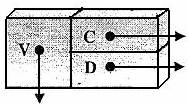
Рис. 2. Элемент образа списка
Интуиция подсказывает, что параллельная обработка списка, заданного в традиционной форме, невозможна. Ясно, как за время log2 N обработать массив длины N, но кажется, что список надо обрабатывать обязательно последовательно, поскольку в общем случае необходимо вычислить адреса к предыдущих элементов списка, прежде чем станет доступен (k + 1)-й элемент. Однако решение этой задачи становится возможным на основе использования образа R списка. При этом целесообразно модифицировать представление каждого элемента массива, отображающего элемент списка, введением дополнительного поля D, представляющего ссылку специального вида. При формировании списка L в поле D заносится ссылка на соответствующее поле того элемента списка, ссылка на который содержится в поле C. Таким образом, элемент образа списка превращается в тройку (V, С, D). На рис. 2 структура элемента образа списка представлена в графической форме.
На рис. 3, A изображен список, соответствующий следующей записи: L = (А В Е FG Н I) (для простоты изложения все примеры будем приводить для списков, не содержащих подсписков).
Пусть над элементами списка L последовательно, начиная с головы, проводится следующее действие: поле D текущего элемента принимает значение того поля D, на которое указывает содержащаяся в нем ссылка. Если в поле D содержится ссылка на пустой элемент, то его значение не изменяется. После выполнения указанного действия над всеми элементами список L примет вид, представленный на рис. 3, В. Вид списка L после второго прохода показан на рис. 3, С. И, наконец, после третьего прохода поле D головы списка будет содержать ссылку на последний элемент списка L, на чем выполнение алгоритма заканчивается (рис. 3, D).
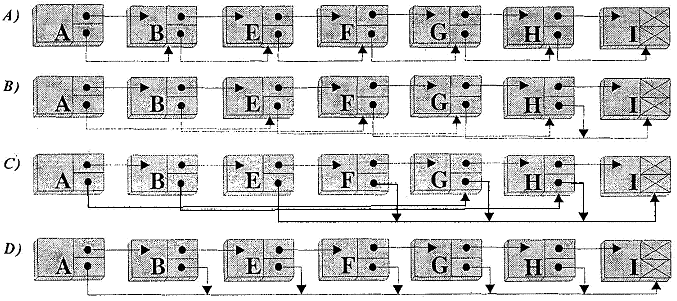
Рис. 3. Нахождение последнего элемента списка (последовательное расположение элементов в памяти)
Предположим теперь ситуацию, когда элементы списка расположены в памяти в произвольном порядке, например так, как показано на рис. 4, А.
На рис. 4, В—D представлен вид списка L соответственно после первого, второго и третьего проходов алгоритма. Как видим, порядок расположения элементов в памяти не влияет на правильность выполнения алгоритма. При этом важно, что преобразования, проводимые во время выполнения алгоритма, не изменяют структуру списка, поскольку действия осуществляются над "избыточной" информацией.

Рис. 4. Нахождение последнего элемента списка (поризвольное расположение элементов в памяти)
Теперь заметим, что все операции над образом списка R, проводимые во время одного прохода, могут быть выполнены параллельно и независимо друг от друга, т. е. при наличии достаточного вычислительного ресурса — за один временной шаг. Алгоритм в целом, таким образом, позволяет получить доступ к последнему элементу списка за Iog2 N временных шагов.
Аналогичные алгоритмы, использующие информационную избыточность, могут быть построены и для других операций над списками. Все они восходят к идеям, высказанным впервые в [6]. В их основе лежит прием распределения элементов списка между процессорами для независимой, а в определенных случаях — и для взаимосвязанной обработки. Некоторые из этих алгоритмов были реализованы на ВС ConnectionMachine (CM) [4].
Примеры
Использование идеи, изложенной в предыдущем разделе, позволяет построить алгоритмы, реализующие операции над списками, для локально-асинхронной ВС.
Решение многих задач обработки больших массивов однородной информации (а именно к ним относятся задачи обработки списков) хотя бы фрагментарно допускает использование принципа монопрограммирования. В этом разделе приводятся монопрограммы, реализующие операции над списками: нахождение последнего элемента списка, поиск и исключение элемента списка, а также прослеживается процесс их выполнения на локально-асинхронной ВС.
Отметим, что применение алгоритмов [4] предполагает обладание еще дополнительной информацией (в частности, о расположении головного элемента списка) и, если число элементов списка превосходит число процессорных элементов, может представлять некоторые трудности.
Как говорилось выше, для организации параллельной обработки целесообразно одновременно с формированием и изменением списка организовывать учет его структуры и структуры памяти в некотором дополнительном образе R списка. Этим образом может быть, например, массив информации об элементах списка, содержащий сведения о структуре списка и преемственности его элементов. Еще раз отметим, что упорядоченность элементов этого массива в памяти в общем случае может не совпадать с логической упорядоченностью элементов списка, задаваемой ссылками. Это позволяет достаточно просто интерпретировать выполнение операций над списками. Например, при добавлении новых элементов в список L нет необходимости вставлять новый элемент массива R в какую-либо конкретную позицию — можно просто добавить его в конец массива. Аналогично, при исключении элемента из L на освободившееся в массиве R место можно, например, записать последний элемент массива Rвместо того, чтобы уплотнять этот массив. Число элементов массива совпадает с числом элементов списка. Обработку списка, тем самым, мы можем попытаться свести к обработке массива, представляющего его образ.
Этот массив, в свою очередь, может описываться дескриптором, что значительно облегчит операции над ним и позволит использовать специальные команды в системе команд.
Многопроцессорная обработка массивов требует применения особых команд, обеспечивающих переадресацию для различных дисциплин выбора "своих" (для обрабатывающего процессора) элементов, анализа выхода за пределы массива, инвариантность программы относительно размера массива. Для выполнения таких операций используются дескрипторы массивов.
Тогда дескриптор DR массива ![]() в полной комплектации содержит восемь элементов DR = {DR0, ..., DR7}. Дескрипторный элемент DR0 содержит адрес a0 первого элемента массива, DR1 содержит шаг h = 3 переадресации, DR2 — число N элементов массива, в DR3 находится адрес последнего элемента массива. Элемент DR4 служит для переадресации при последовательном обращении к данному массиву. В нем хранится адреса0 + jh для выработки элемента массива при j-м (j = 0, 1,...) обращении к массиву. При каждом обращении к массиву по некоторым командам этот адрес увеличивается на шаг hт. е. выполняется операция j: = j + 1. Следующая группа дескрипторных элементов предназначена для организации распределения элементов массива между процессорами. В DR5 содержится значение адреса а0 + jh, i = 0, 1, ..., n- 1, т. е. каждый процессор Пi,- формирует и использует свое значение (DR5), располагая адресом регистра, содержащего значение номера i процессора, для начального обращения к "своему" элементу массива. В DR6 содержится значение nh, используемое для переадресации к следующему "своему" элементу массива с учетом числа процессоров в ВС. В DR7 содержится значение адреса a0 + ih + jnh = (DR5) + j(DR6), используемое для возможности переадресации при последовательном обращении к массиву (j = 0, 1, ...) с учетом начального обращения к "своему" элементу массива и последующего изменения адреса элемента на величину nh, хранимую в DR6.
в полной комплектации содержит восемь элементов DR = {DR0, ..., DR7}. Дескрипторный элемент DR0 содержит адрес a0 первого элемента массива, DR1 содержит шаг h = 3 переадресации, DR2 — число N элементов массива, в DR3 находится адрес последнего элемента массива. Элемент DR4 служит для переадресации при последовательном обращении к данному массиву. В нем хранится адреса0 + jh для выработки элемента массива при j-м (j = 0, 1,...) обращении к массиву. При каждом обращении к массиву по некоторым командам этот адрес увеличивается на шаг hт. е. выполняется операция j: = j + 1. Следующая группа дескрипторных элементов предназначена для организации распределения элементов массива между процессорами. В DR5 содержится значение адреса а0 + jh, i = 0, 1, ..., n- 1, т. е. каждый процессор Пi,- формирует и использует свое значение (DR5), располагая адресом регистра, содержащего значение номера i процессора, для начального обращения к "своему" элементу массива. В DR6 содержится значение nh, используемое для переадресации к следующему "своему" элементу массива с учетом числа процессоров в ВС. В DR7 содержится значение адреса a0 + ih + jnh = (DR5) + j(DR6), используемое для возможности переадресации при последовательном обращении к массиву (j = 0, 1, ...) с учетом начального обращения к "своему" элементу массива и последующего изменения адреса элемента на величину nh, хранимую в DR6.
При отсутствии необходимости могут формироваться не все дескрипторные элементы. В частности, не во всех случаях обработка элементов массива распределяется между процессорами. Для таких массивов формирование дескрипторных элементов DR5, DR6 и DR7 может не потребоваться.
Назначение дескрипторных элементов позволяет включить в состав системы команд ряд команд изменения содержимого дескрипторов и выполнения операций над определенными элементами массива.
В BC реализована трехадресная система команд (отраженная в ассемблере) вида:
![]() ,
,
где ![]() — код операции; I1; I2, I3 — адреса модификаторов, дескрипторов, дескрипторных элементов; A1, A2, A3, — смещения.
— код операции; I1; I2, I3 — адреса модификаторов, дескрипторов, дескрипторных элементов; A1, A2, A3, — смещения.
По этой команде формируются исполнительные адреса:
![]()
В заключение заметим, что посредством одного набора дескрипторов можно описывать несколько списков одновременно. Легко видеть, что в этом случае приведенный выше алгоритм позволяет найти последние элементы всех списков за один полный цикл своей работы.
Нахождение последнего элемента списка. Пусть список L размещен в оперативной памяти данных. Элементы его расположены не в порядке следования, а в соответствии с динамикой формирования, включения и исключения элементов и в зависимости от наличия свободных областей памяти необходимого объема.
В памяти также расположен образ списка, представленный массивом R. Кроме того, считаем, что уже сформирован дескриптор, описывающий этот массив (с учетом того, что некоторые дескрипторные элементы, в частности, DR5 и DR7, формируются для каждого процессора с использованием его номера).
Необходимо найти последний элемент списка, используя приведенный выше алгоритм.
Программа, реализующая этот алгоритм, представлена на рис. 5.
N |
| I1 | A1 | I2 | A2 | I3 | A3 |
0 | СИНХ |
|
|
|
|
|
|
1 | ЗАГ | K |
|
|
|
|
|
2 | ПРАД | DR7 |
|
|
|
| 012 |
3 | УП≠0 |
| K |
|
|
| 012 |
4 | ЗАПК | DR7 | 0003 |
|
|
| M |
5 | УП=0 |
| M |
|
|
| 01 |
6 | ЗАПК |
| M |
|
| DR7 | 0003 |
7 | ИЗМАД | DR7 |
|
|
|
| 009 |
8 | БП |
| 003 |
|
|
|
|
9 | ЗАГ | DR7 | DR5 |
|
|
|
|
10 | БП |
| 003 |
|
|
|
|
11 | ЗАП | DR7 | 0003 |
|
|
| K |
12 | В |
|
|
|
|
|
|
Рис. 5. Программа нахождения последнего элемента списка
Команда 0 (СИНХ) синхронизирует процессоры для одновременного начала выполнения ими программы. Отметим, что порядок начала выполнения программы на процессорах не влияет на правильность работы ВС, а лишь упрощает контроль выполнения монопрограммы. По этой команде каждый процессор посылает сигнал на устройство СИНХ. При поступлении таких сигналов от всех процессоров приходит обратный сигнал, по которому процессоры приступают к выполнению следующей команды.
Команда 1 ("ЗАГрузка модификатора") обнуляет модификатор K, в который впоследствии одним из процессоров будет записан адрес последнего элемента списка.
Команда 2 ("ПРоверка АДреса") сравнивает значение дескрипторного элемента DR7, которое первоначально предполагается равным a0 + 3i, с адресом последнего элемента массива, записанным в дескрипторном элементе DR3. Этим устанавливается возможность загрузки i-го процессора (возможен случай i > N). Если процессор не будет занят обработкой списка, управление передается команде 12 на "Выход из процедуры". В противном случае с команды 3 начинается цикл обработки элементов списка, а точнее — его последовательности ссылок.
Команда 3 осуществляет "Условный Переход" на выход из процедуры по отличному от нуля значению K.
Команда 4 — "ЗАПись по Косвенному адресу" — выполняется при нулевом значении K. По этой команде проводится косвенное считывание по первому адресу (DR7) + 0003, т. е. по адресу ((DR7) + 0003), и запись по адресу модификатора М (мы считаем, что система ссылок, отражаемая в полях D, организована по принципу косвенности, т. е. ссылка в элементе списка является адресом ссылки следующего элемента).
Команда 5 проверяет, пуста ли выбранная ссылка. Если пуста, то анализируемый элемент списка является последним; управление передается команде 11, по которой адрес этой ссылки записывается в K. Если ссылка не пуста, т. е. (М) ≠ 0, то выполняется команда 6, и ее значение записывается вместо значения текущей ссылки.
По команде 7 ("ИЗМенение АДреса") проводится операция (DR7): = (DR7) + (DR6) и, если полученное значение превышает (DR3), управление передается на выполнение команды 9. Таким образом, каждый процессор осуществляет переадресацию для последующей выборки "своего" адреса ссылки из массива таких адресов. Если при этом массив не исчерпан, команда 8 ("Быстрый Переход") передает управление на команду 3 — продолжение цикла подстановки ссылок. Если переадресация выводит из массива, то команда 9 восстанавливает дескрипторный элемент DR7 (выполняется операция (DR7): = (DR5) = a0 + 3i) и командой 10 управление передается на следующий цикл подстановки ссылок.
Команда 11 выполняется, если в процессе выполнения команды 5 обнаружилось, что найдена пустая ссылка, адрес которой записывается в К. После выполнения в последующем команды 3 всеми процессорами закончится и выполнение программы.
Рассмотрим процесс счета программы нахождения последнего элемента списка L, содержащего семь элементов (который изображен на рис. 3, А), на BC, имеющей в составе три процессора — П0, П1, П2. Каждый процессор выполняет свою копию программы, обладая при этом своим собственным набором дескрипторов (отличающихся друг от друга только значениями дескрипторных элементов DR5 и DR7). Согласно принятым нами представлению образа списка и порядку его обработки процессор П0 будет обрабатывать элементы списка A, Fи I, процессор П1 — B и G, и процессор П2 — элементы E и H.
Предположим для простоты, что каждая команда программы выполняется за одинаковое время — условный такт, и при обращении к памяти не возникает конфликтов (все элементы образа списка расположены в разных блоках памяти). На рис. 6 представлена диаграмма потактового выполнения программы на каждом из процессоров, полученная при справедливости этих предположений. Некоторое время все процессоры работают синхронно: такты 1—3 — начальные действия; такты 4—9 — первый цикл подстановки ссылок, во время которого изменяются ссылки (поле D) элементов A, B и E; такты 10—12 — начало второго цикла подстановки ссылок.

Рис.6. Временная диаграмма выполнения программы нахождения последнего элемента списка
Во время второго цикла подстановки ссылок процессор П2 обнаруживает ссылку на пустое значение, т. е. обнаруживает последний элемент списка (такт 12) и, осуществив запись его адреса в модификатор K(такт 13), заканчивает свою работу выполнением в следующем такте команды "Возврат".
Процессор П0 заканчивает второй цикл подстановки ссылок (такты 13—15), не обнаружив пустой ссылки, но завершает свою работу в тактах 16 и 17, поскольку модификатор K получил уже к этому времени ненулевое значение.
Процессор П1 в такте 14 изменяет значение дескрипторного элемента DR7 и, так как оно выходит за границы обрабатываемого массива, в такте 15 восстанавливает его исходное значение. Далее следует переход на начало третьего цикла обработки ссылок (такт 16), но после обнаружения ненулевого значения модификатора K (такт 17) в следующем такте процессор П1 также завершает свою работу.
Результатом совместной работы трех процессоров является, таким образом, адрес ссылки на последний элемент списка, записанный в модификаторе K.
Легко заметить, что детерминированный — при синхронной работе многих процессорных элементов — характер процесса выполнения алгоритма при реализации на локально-асинхронной BC может приобрести некоторую неопределенность.
Действительно, при реализации алгоритма на ConnectionMachine (СМ) все процессорные элементы (ПЭ) одновременно выбирают информацию из поля D своего преемника. При этом не возникает конфликтов ни при выборке (так как память ПЭ разделена), ни при передаче по коммуникационной сети (информация передается только одному соседнему ПЭ). При реализации же на локально-асинхронной BC мы не можем быть уверены в порядке выполнения процессорами операций замены значений ссылок (команда 6), поскольку в принципе не исключены обращения к одним и тем же модулям общей памяти. В результате возникает возможность того, что какой-либо процессор "подхватит" уже обновленную ссылку, однако очевидно, что ввиду однонаправленности ссылок это не может отсрочить окончание работы алгоритма, а только приблизить.
Алгоритм в этом случае как бы "перескакивает" через некоторые шаги. Например, элемент A, обрабатываемый процессором П0, после первого выполнения процессором команды 6 должен содержать ссылку на элемент E. Однако, если процессор П1 в силу каких-либо причин успел выполнить свою аналогичную операцию раньше, элемент A будет содержать ссылку на более "удаленный" от него элемент F. Поэтому появляется вероятность более раннего достижения условия окончания работы программы.
Отметим, что возможность нахождения последнего элемента списка является основой для реализации многих операций над списками. Например, для построения функции APPEND, объединяющей два списка L1 и L2, достаточно найти последний элемент списка L1 и заменить в его поле C пустую ссылку ссылкой на адрес первого элемента списка L2.
Поиск и исключение элемента списка. Пусть задано имя S некоторого элемента списка, являющееся первым словом в массиве его данных, на которое указывает одна из ссылок C в массиве R троек (K, С, D). Необходимо по заданному Sнайти соответствующий ему элемент списка, т. е. такой, данные которого начинаются с S, и исключить его из списка. Для этого достаточно заменить значение ссылки C в одной из троек в массиве R, указывающей на исключаемый элемент, на значение ссылки, указанное в тройке, соответствующей исключаемому элементу. При этом тройка, соответствующая исключаемому элементу, в свою очередь должна быть исключена из массива R.
Совместные действия процессоров можно организовать следующим образом.
Пусть все процессоры "смотрят" на соответствующие им по номеру (а затем — кратные их номеру) элементы массива R. Какой-то из них найдет элемент, ссылка в котором указывает на элемент списка, первое слово в котором совпадает с S. Эта ссылка заменяется тем же процессором на ссылку, указанную в исключаемом элементе, а сам элемент массива R, соответствующий исключенному элементу, исключается из R. После этого корректируется дескриптор, соответствующий массиву R.
Проанализируем работу программы, представленной на рис. 7.
N |
| I1 | A1 | I2 | A2 | I3 | A3 |
0 | СИНХ |
|
|
|
|
|
|
1 | ≠ | <i> |
|
|
|
| 003 |
2 | ЗАГ | K |
|
|
|
|
|
3 | ПРАД | DR7 |
|
|
|
| 010 |
4 | ЗАП | DR7 | 0002 |
|
|
| M1 |
5 | ЗАПК | M1 | 0001 |
|
|
| M2 |
6 | ≠ |
| M2 |
| S |
| 011 |
7 | ЗАГ | K | 001 |
|
|
|
|
8 | ЗАП | M1 | 0002 |
|
| DR7 | 0002 |
9 | ИСКЛ | DR |
| M1 |
|
|
|
10 | В |
|
|
|
|
|
|
11 | ≠ | K |
|
|
|
| 010 |
12 | ИЗМАД | DR7 |
|
|
|
| 010 |
13 | БП |
| 004 |
|
|
|
|
Рис. 7. Программа поиска и исключения элемента из списка
По команде 0 осуществляется синхронизация процессоров ВС.
По командам 1 и 2 нулевое значение присваивается модификатору K. Другие процессоры по команде 1, в которой номер i процессора сравнивается с нулем и выполняется Условный Переход по неравенству, перейдут к выполнению команды 3. Таким образом иллюстрируется возможность параллельной работы процессоров по разным ветвям монопрограммы.
По команде 3 осуществляется выход из программы, если значение текущего адреса в дескрипторном элементе DR7 превосходит значение адреса последнего элемента массива R, записанное в DR3. Если (DR7) ≤ (DR2), в регистр M заносится ссылка анализируемого элемента списка, записанная по адресу (DR7) + 2 — т. е. в поле C.
Пусть ссылка, записанная в поле C, указывает на первый адрес в тройке, составляющей некоторый элемент R. Тогда по адресу (М1) + 1 находится адрес начала "тела" соответствующего элемента списка. Команда 5 выполняет запись по косвенному адресу этого начала в регистр М2.
По команде б сравнивается начало тела анализируемого элемента списка с исключаемым элементом, указанным в S.
При положительном результате сравнения по команде 7 модификатору K присваивается отличное от нуля значение, служащее индикатором того, что исключаемый элемент списка некоторым процессором найден. Если (М2) ≠ (S), управление передается команде 11.
По команде 8 ссылка, записанная в элементе массива R и соответствующая исключаемому из списка элементу, присваивается тому элементу, который ранее указывал на исключаемый, т. е. значение ((M1) + 2) присваивается элементу (DR7) + 2.
Команда 9 — ИСКЛючение из массива, описываемого дескриптором DR, элемента, расположенного по адресу (М1). В соответствии с выполнением команды 4 по данному адресу находится элемент массива R, соответствующий исключаемому из списка элементу.
По команде 10 осуществляется выход из подпрограммы.
Команда 11 получает управление в случае, если ссылка в анализируемом элементе массива R не указывает на исключаемый из списка элемент. В этом случае проверяется наличие признака того, что некоторый процессор обнаружил искомый элемент и готов его исключить из списка, т. е. если (K) ≠ 0, осуществляется выход из подпрограммы по команде 10. Если (K) = 0, необходимо перейти к анализу следующего элемента массива R, предопределенного i-му процессору.
По команде 12 выполняется переадресация вида (DR7): = (DR7) + (DR6), где (DR6) = Nh. Если такая переадресация приводит к выходу за пределы массива, т. е. новое значение DR7 превышает значение последнего адреса массива R, указанное в DR3,, осуществляется выход из подпрограммы по команде 10.
В противном случае по команде 13 процессор приступает к анализу очередного элемента R.
В данном случае нам не пришлось в полной мере использовать существующие в системе средства синхронизации. Легко усложнить пример, рассмотрев случай, когда одновременно заданы несколько таких элементов. Тогда видно, что исключение каждого из них должно проводиться последовательно, так как процессор, обнаруживший исключаемый элемент, должен располагать вполне определенной информацией о текущем состоянии списка, изменяемом в процессе исключения из него элементов. Ведь после каждого исключения может измениться и порядок последующего назначения элементов массива R на обработку процессорами.
Это приводит к необходимости выделения одной или группы команд исключения из списка (см. команду 9 данной монопрограммы) в критический блок, не допускающий одновременного обращения к нему более одного процессора. Формирование критического блока достигается выполнением в его начале команды ЗАКРыть Семафор с указанием адреса некоторого семафора C. Если при выполнении этой команды данный семафор уже закрыт другим процессором при выполнении этого же фрагмента программы, то процессор переходит в режим ожидания — фактически, повторного выполнения этой команды до открытия семафора.
Критический блок заканчивается командой ОТКРыть Семафор с указанием адреса того же семафора.
* * *
Целью данной статьи является иллюстрация не всегда ясно осознаваемого факта, что принципы параллельной обработки информации могут быть использованы для нахождения самого общего решения задач, казалось бы, по своей природе нераспараллеливаемых. Эффективность параллельной обработки списков в нашем случае достигается двумя встречными путями: дополнением традиционного ограниченного подхода к методам обработки списков концепцией обработки массивов и использованием архитектурных особенностей предлагаемой ВС. Последние предполагают построение системы на основе совместной работы большого числа процессоров на общей памяти, возможность их синхронизации на уровне выполнения команд (без использования ОС), ориентацию системы команд на реализацию различных дисциплин обработки массивов, возможность выполнения копий единой для всех процессоров программы (см. также [7]).
Список литературы
1. Фостер Дж. Обработка списков. М.: Мир, 1974. 102 с.
2. Кнут Д. Искусство программирования для ЭВМ. Т. 1. Основные алгоритмы. М.: Мир, 1978. 734 с.
3. Шабанов Л.В. Организация временных списков на векторно-конвейерной ЭВМ // Вопросы кибернетики. Эффективное использование высокопроизводительных ЭВМ. НС по комплексной проблеме "Кибернетика" АН СССР, 1985. С. 110—124.
4. Hillis W., Stcele G. Data Parallel Algorithms // Communications of the ACM. 1986. V. 29, N 12. P. 1170-1183.
5. Барский А. Б. Монопрограммные высокопараллельные локально-асинхронные вычислительные структуры // Вопросы кибернетики. Эффективные вычисления на супер-ЭВМ. НС по комплексной проблеме "Кибернетика" АН СССР, 1988. С. 148-170.
6. Minsky M., Papert S. Perceptrons, 2 nd ed. MIT Press, Cambridge, Mass. 1979. 256 p.
7. Barsky А. В., Shilov V. V. Highly Parallel Asynchronous Computer Systems For The Large Data Arrays Processing // Proc. SMS TPE'94. M.: ISP RAS, 1994. P. 238-247.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 6, 1999
ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ И СЕТИ
Ключевые слова: Параллельные вычисления, SPMD-архитектура, списковые структуры, операции со списками, локально-асинхронные системы.
Публикации с ключевыми словами: параллельные вычисления, SPMD-архитектура, списковые структуры, операции со списками, локально-асинхронные системы
Публикации со словами: параллельные вычисления, SPMD-архитектура, списковые структуры, операции со списками, локально-асинхронные системы
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



