научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#2 февраль 2006
А. Ю. Щеглов, д-р техн. наук, проф., СПб ГИТМО (ТУ)
Задачи и методы статического оптимального кодирования относительных приоритетов заявок на обслуживание в мультипроцессорной вычислительной системе и ЛВС реального времени
Рассматриваются альтернативные методы оптимального кодирования относительных приоритетов заявок и методы их изменения по расписанию для обеспечения функционирования вычислительной системы в реальном времени. Обсуждаются задачи, критерии оптимальности и методы синтеза статистических кодов, неизменяемых во времени или в процессе функционирования системы.
Предложенная автором концепция обслуживания заявок на доступ к общим ресурсам в вычислительной системе или в ЛВС в реальном времени основана на реализации дисциплины обслуживания с относительными приоритетами, изменяемыми по расписанию (в том числе и по приоритетному). Данный подход позволяет получить оригинальные дисциплины обслуживания для рассматриваемой области приложений. Предлагаемый подход реализуется принципами кодового управления множественным доступом абонентов системы к ресурсам реального времени, обеспечивающими эффективную передачу полномочий в системе на занятие ресурса [1 — 12].
Целью работы является рассмотрение альтернативных методов оптимального кодирования относительных приоритетов заявок* (*Заявка — запрос на выполнение определенной работы, поступающий от абонента к общему ресурсу.) и методов их изменения по расписанию для обеспечения функционирования системы в реальном времени. Обсуждаются задачи, критерии оптимальности и методы синтеза статических кодов приоритетов, под которыми понимаются коды, не изменяемые во времени или в процессе функционирования системы.
Модель системы реального времени. Так как основными требованиями к качеству построения и функционирования вычислительной системы (ВС) реального времени является выполнение временных ограничений в обслуживании заявок, то рассредоточенную ВС реального времени можно описать детерминированной моделью. К временным параметрам обслуживания заявок относятся величины: Tpm — продолжительность занятия ресурса m-м, m = 1, ..., M, абонентом для информационного с ним взаимодействия; Tппm — продолжительность передачи прав m-му абоненту после освобождения ресурса в системе; Ki(m) — коэффициент частоты занятия ресурса i-м, i = 1,..., M, абонентом относительно m-го, i ≠ m.
Качество обслуживания заявок можно описать характеристиками: Tam — продолжительность арбитража требования m-го абонента (с момента появления заявки до момента предоставления абоненту права занять ресурс) или продолжительность ожидания заявкой обслуживания; Tom — продолжительность обслуживания заявки системой.
Для систем реального времени интерес представляют граничные (худшие для любой заявки) значения рассмотренных характеристик, которые соответственно обозначим: Trрm; Trппm; Kri(m); Tram; Trom; i, m = 1,…,M, i ≠ 1 параметры обслуживания заявок в системе реального времени: Tram, Trom.
С учетом сказанного получаем модель системы реального времени:
 (1)
(1)
Утверждение. Обслуживание заявки в реальном масштабе времени корректно, если для любого абонента системы m, m = 1, ..., M выполняются условия (1).
Доказательство. Если условие (1) хотя бы для одного абонента системы не выполняется, нельзя считать, что его заявки обслуживаются в реальном масштабе времени, так как его параметры обслуживания Tam и Tom в этом случае не могут быть ограничены сверху и, следовательно, всегда найдутся условия функционирования системы, при которых Tram < Tam и Trom < Tom или заявка будет обслужена не в реальном времени, т. е. для системы она потеряна.
С учетом сказанного под заявкой реального времени следует понимать заявку, которая будет потеряна, если не обслужится системой за некоторый фиксированный интервал времени с момента поступления.
Идея кодового управления множественным доступом. В основе предлагаемого подхода лежат следующие принципы кодового управления в реальном масштабе времени [1—12].
1. В любой момент времени функционирования системы матрице относительных приоритетов (ОП) абонентов системы (абонент — пользователь общего ресурса вычислительной системы или сети) ставится во взаимно однозначное соответствие матрица кодов относительных приоритетов (МКП). Строки МКП соответствуют строкам матрицы приоритетов (МП), а столбцы задают код ОП очереди заявки. Пример МКП в предположении, что "1" в разряде кодового слова приоритетнее "0" (по "1" права передаются, по "0" — нет) и что приоритет разряда кода убывает по мере возрастания его порядкового номера, приведен на рис. 1.
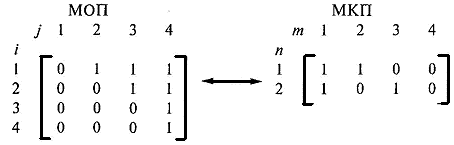
Рис. 1. Пример отображения МОП в МКП
2. В процессе функционирования системы при каждом занятии ресурса МКП изменяется в соответствии со сменой исходной МП (заменой МП на МКП во все моменты времени ts, задаваемые занятием ресурса системы), в результате чего получается граф смены МКП (чем и реализуется передача прав по расписанию). Пример графа МКП для случая бесприоритетного обслуживания (обслуживание в циклическом порядке) приведен на рис. 2.
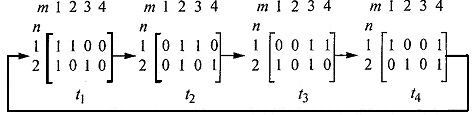
Рис. 2. Пример графа изменения МКП по бесприоритетному расписанию
3. При управлении доступом к ресурсу должно осуществляться поразрядное (начиная с более приоритетных разрядов) сравнение кодов ОП заявок, затребовавших к данному моменту времени ресурс, с "отключением" по каждому разряду менее приоритетных заявок; при однозначном кодировании заявок получаем бесконфликтное занятие ресурса.
Принципы оптимального кодирования ОП абонентов. Выше отмечалось, что при кодовом управлении множественным доступом осуществляется арбитраж заявок по каждому разряду кода ОП nm, nm = 1, ..., Nm (их число при равномерном коде составляет [logDM], где D — основание кода), на каждый из которых приходятся удельные затраты Tynm, откуда получаем, что затраты времени на передачу прав абоненту для занятия ресурса (арбитраж) составляют
![]() (2)
(2)
Выражение (2) определяет альтернативные пути уменьшения затрат времени Trппm на управление множественным доступом при кодовом
управлении, задаваемые изменением параметров Nm
и Tynm.
Первый из них может быть сформулирован в постановке задачи оптимального
кодирования: для заданного вероятностного ансамбля 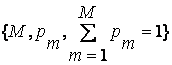 [13], где pm — распределение вероятностей заявок на
множестве M, найти множество кодов ОП длиной Nm, m = 1, ...,
M, обращающих в минимум среднюю скорость
кодирования
[13], где pm — распределение вероятностей заявок на
множестве M, найти множество кодов ОП длиной Nm, m = 1, ...,
M, обращающих в минимум среднюю скорость
кодирования
Для решения рассмотренной классической задачи теории информации может быть использован метод Хаффмена [13]. Альтернативный подход — снижение потерь Trппm за счет уменьшения Tynm связан с выбором механизма передачи прав на доступ к ресурсу между абонентами системы. Этот вопрос исследован в [4, 12].
Если рассмотреть зависимость

где Is — информативность смеси в канале данных; ![]() и
и ![]() —
соответственно длина (в байтах) кода приоритета абонента и информационного
кадра, то можно сделать вывод, что для равномерного и предельно неравномерного
кодов данный метод эффективен при малых
—
соответственно длина (в байтах) кода приоритета абонента и информационного
кадра, то можно сделать вывод, что для равномерного и предельно неравномерного
кодов данный метод эффективен при малых ![]() , т. е. в приложениях
вычислительных систем и ЛВС, связанных с построением управляющих вычислительных
систем реального времени.
, т. е. в приложениях
вычислительных систем и ЛВС, связанных с построением управляющих вычислительных
систем реального времени.
Особенностью иной постановки задачи оптимального кодирования ОП будет необходимость учета более высокого приоритета уровня "1" над уровнем "0" (пусть исходно так задано) в каждом разряде кода ОП, так как по значению "1" в разряде кода приоритета абоненту предоставляется право занять ресурс, по значению "0" — не предоставляется. Множество абонентов с заданной на нем вероятностью p требований общего ресурса, одинаковой для всех абонентов системы, представляет собой математическую модель равномерного поэтапного кодирования/декодирования (или просто поэтапного кодирования) пользователей общих ресурсов: {M, N, 0 ≤ р ≤ 1, m = 1, M, n = 1, N}. Величина p здесь является характеристикой интенсивности поступления в систему требований ресурса.
Под величиной Pn(p) будем понимать вероятность однозначного декодирования m-го абонента по n из N разрядам кода приоритета при вероятности р обращения абонентом к общему ресурсу системы. Рассмотрим изменение величины Pn(p) при n = 1; 2; 3, соответственно Pn=1, 2, 3(р) при изменении р. Зависимости Pn(р) = f(p) для случая M = 8 представлены на рис. 3, из которого следует, что при невысоких загрузках системы вероятность однозначного декодирования абонента с увеличением длины кодового слова изменяется не в сильной степени, откуда может быть сделан вывод, что способ кодирования по всем N разрядам кода приоритета (имеется в виду равномерный код) в общем случае избыточен, особенно при малых загрузках системы.
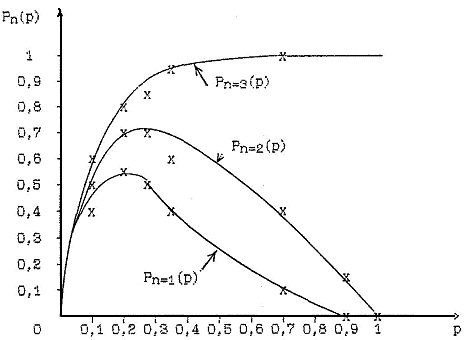
Рис. 3. Иллюстрация эффективности поэтапного кодирования
Другими словами, выше рассмотрен принцип поэтапного кодирования, состоящий в управлении множественным доступом поэтапно — по частям кода приоритета, с увеличением длины кода на каждом этапе и, как следствие, при возможности неоднозначного декодирования абонента по используемой части кода приоритета — на всех этапах, кроме последнего. Нетрудно показать, что скорость поэтапного кодирования максимальна при использовании всех TV разрядов в коде приоритета.
Замечание. Особенностью реализации принципа поэтапного кодирования является возможность предоставления права занять ресурс одновременно нескольким абонентам, что требует обнаружения конфликта информации в канале, что, в свою очередь, будет являться условием необходимости увеличения длины кода приоритета. Принцип поэтапного кодирования предполагает конфликтную передачу прав между абонентами системы на занятие ресурса, реализацию конфликтного метода управления множественным доступом.
Конфликты при поэтапном кодировании возможны потому, что по части кода приоритета абонента (по младшим разрядам) в общем случае не может быть однозначно идентифицирован абонент, например, код 101 по трем младшим разрядам имеют абоненты с кодами приоритета 1010 и 1011.
Влияние условия — ОП "1" над "0" при занятии ресурса, которое необходимо учитывать при кодировании приоритетов абонентов, рассмотрим на простом примере. Определим вероятность однозначного декодирования абонента по одному разряду кода приоритета (имеется в виду — только по первому разряду n = 1, естественно, в предположении, что здесь возможен конфликт), например для случая M = 4, т. е. рассмотрим следующие кодовые комбинации: ООП, 0001, 0111. Имеем: для комбинации ООП Pn – 1(p) = 2p(1 - p); для комбинации 0001 Pn=1(p) = p; для комбинации 0111 Pn – 1(p) = 3p(1 - p)2.
Зависимости Pn=1(p) = f(p) для рассматриваемых случаев представлены на рис. 4. На основании рисунка могут быть сделаны следующие выводы:
· эффективность способа кодирования зависит от изменения р;
· могут иметь место интервалы изменения величины р, когда неравномерное кодирование абонентов (неравное число единиц и нулей в кодовой комбинации) эффективнее равномерного кодирования (соответственно число нулей и единиц в кодовой комбинации совпадает).

Рис. 4. Иллюстрация влияния условия ОП "1" над "0" на эффективность занятия ресурсов
На рис. 4, в частности, видим, что на интервале изменения параметра 0 ≤ р ≤ р1 эффективнее код 0111, на интервале изменения p1 < р ≤ р3 — код 0011, на интервале изменения р2 < р < 1 — код 0001.
Предельными случаями неравномерных кодов являются соответственно предельно неравномерные по "0" и по "1" коды, примеры которых для случая M = 4 представлены соответственно на рис. 5, первый из которых эффективен при р → 1, второй при р → 0, причем предельно неравномерный по "0" код обеспечивает поэтапный бесконфликтный арбитраж (бесконфликтное кодирование). Особенностью этих кодов будет максимальная эффективность соответственно при низкой и высокой загрузках системы. Другими словами, предельно неравномерные коды, по существу, представляют собой предельные случаи кодирования, ориентированные соответственно на низкую и высокую загрузки системы, а любой применяемый на практике неравномерный код будет занимать промежуточное положение между равномерным кодом ОП и соответствующим предельно неравномерным по "О" или по "1" кодом.
Эффективность неравномерного поэтапного кодирования можно оценить по критерию "скорость однозначного поэтапного неравномерного кодирования по Nm разрядам"

где ![]() — вероятность
однозначного декодирования абонентов по разрядам nm
кода ОП.
— вероятность
однозначного декодирования абонентов по разрядам nm
кода ОП.
На простейшем примере (M = 4) покажем, что полученные нами выше результаты распространяются и на случай декодирования по всему коду приоритета (соответственно по Nm кодовым комбинациям).
Под полной математической моделью поэтапного кодирования приоритетов абонентов будем понимать математическую модель равномерного поэтапного кодирования, учитывающую параметр pm, или кодовую вероятностную модель, учитывающую параметр р. Особенностью полной математической модели будет наличие уже двух параметров р и pm, различно влияющих на выбор оптимального способа кодирования: р задает возможность эффективного поэтапного кодирования, в результате в качестве оптимального может быть получен неравномерный код; pm задает возможность эффективного полного кодирования, в результате также в качестве оптимального может быть получен неравномерный код, причем в общем случае эти оптимальные неравномерные коды могут не совпадать.

Рис. 5. Примеры предельно неравномерных кодов приоритетов:
а — предельно неравномерный код по "1"; б — предельно неравномерный код по "0"
В качестве критерия оптимальности так же, как и для модели поэтапного
кодирования, должен использоваться параметр ![]() — математическое ожидание
скорости однозначного декодирования пользователя. Условием оптимальности выбора
способа кодирования будет
— математическое ожидание
скорости однозначного декодирования пользователя. Условием оптимальности выбора
способа кодирования будет ![]() ; с учетом дискретности исходного
набора альтернативных вариантов кодирования имеем
; с учетом дискретности исходного
набора альтернативных вариантов кодирования имеем

где ![]() — параметр
— параметр ![]() для k-го способа кодирования из сравниваемого множества
вариантов K, где
для k-го способа кодирования из сравниваемого множества
вариантов K, где
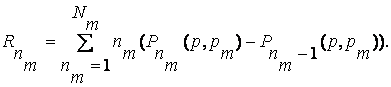
Заметим, что в отличие от соответствующих формул, приведенных ранее, здесь уже учитывается не только число единиц в кодовых комбинациях разряда кодов ОП абонентов, но и то, каким абонентам (соответственно, с какими значениями параметра pm) принадлежат значения единиц.
Утверждение. Всегда можно построить оптимальный код, который будет эффективнее случайного назначения кодов ОП.
Доказательство. Нетрудно показать, что метод случайного задания кодов ОП в среднем имеет характеристики обслуживания ниже, чем метод равномерного поэтапного кодирования, который неэффективен при низких и высоких загрузках системы. В области эффективного использования равномерного кода случайное задание кодов ОП неэффективно, так как не гарантирует однозначного декодирования абонента по Nm разрядам кода.
Данное утверждение приведено для того, чтобы показать, что в рамках концепции кодового управления (в частности, при оптимальном кодировании ОП абонентов) всегда можно получить конфликтный способ управления множественным доступом, который будет эффективнее для конкретных приложений, широко используемых в ЛВС случайных методов.
Принципы приоритетного кодирования ОП абонентов. Определяющим при реализации оптимального способа кодирования является эффективное использование общего ресурса абонентами ВС. Однако, как следует из (1), изменением значения Tппm можно задавать (изменять) приоритет абонента, влияя при этом на гарантированное время обслуживания заявки. Это актуально при небольшой величине информационного кадра. Выполнение данного условия характерно не только для управляющих, но и для информационных ВС и ЛВС. Например, при M = 256 в рамках сетевой технологии ATM [14] получаем, что затраты Tппm составляют 15 % затрат времени на передачу информационного кадра (8/53). Для управляющих ВС длина информационного кадра составляет единицы байтов, т. е. относительные затраты на управление множественным доступом еще выше.
В рамках кодирования ОП абонентов может быть реализован принцип приоритетного кодирования, который состоит в кодировании ОП более важного абонента более коротким кодовым словом в целях минимизации продолжительности доступа к ресурсу именно более приоритетного пользователя. Такой подход целесообразен, когда необходим учет важности абонентов, но в общем случае он не дает оптимального кода в смысле эффективного использования ресурса, так как при кодировании приоритетов здесь уже учитываются не параметры потока требований ресурса, а исключительно важность абонентов друг относительно друга. Таким образом, под приоритетным будем понимать такое кодирование приоритетов абонентов в системе с множественным их доступом к общим ресурсам, при котором целью кодирования является учет относительной важности абонентов.
Замечание. По существу, это также метод оптимального кодирования, но эффективность использования ресурса здесь уже определяется не характеристиками входного потока его требований, а возможностью назначения приоритетов реального времени абонентов в соответствии с ограничениями на время обслуживания их заявок на занятие ресурса в системе.
Постановка задачи приоритетного кодирования выглядит следующим образом.
Пусть задано множество абонентов системы {M, m = 1, ..., M},
характеризуемых различной важностью, которую требуется учитывать реализацией
заданных соотношений длин кодов ОП Nm,
m = 1, ..., M.
Требуется осуществить кодирование ОП — сопоставить множеству абонентов M множество кодов приоритетов ![]() , каждое из которых имеет
исходно заданную длину Nm,
обеспечивающее взаимно однозначное отображение множества абонентов во множество
кодовых слов и наоборот.
, каждое из которых имеет
исходно заданную длину Nm,
обеспечивающее взаимно однозначное отображение множества абонентов во множество
кодовых слов и наоборот.
Рассмотрим метод приоритетного кодирования или метод построения в ВС приоритетных кодов ОП абонентов. Очевидно, что прежде всего при решении рассматриваемой задачи кодирования необходимо определить допустимые соотношения длин кодов приоритетов в системе, что позволит проверить возможность построения кода приоритета с заданным соотношением длин кодов, а при невозможности — скорректировать задаваемое соотношение. Другими словами, имея исходно заданные соотношения длин кодов, необходимо определить возможность построения приоритетного кода в принципе.
Например, возможно ли осуществить приоритетное кодирование с основанием 2 семи абонентов системы кодами приоритетов с длинами (числом разрядов): 2, 2, 3, 3, 3, 3, 4? Имея положительный ответ на данный вопрос, уже можно приступать к решению собственно задачи кодирования.
Возможность построения приоритетного кода с заданными длинами кодов ОП абонентов (в общем случае неравномерного) в полной мере определяется свойствами однозначного кодирования. Поэтому здесь можно использовать неравенство Крафта для префиксных кодов [13], которое гласит, что для существования префиксного кода в алфавите объема D с длинами кодов Nm необходимо и достаточно, чтобы выполнялось условие
 (3)
(3)
С использованием этого неравенства может быть сформулировано условие допустимости соотношений длин кодов приоритетов абонентов при их приоритетном кодировании кодом с основанием D, а именно: может быть выбрано соотношение длин кодовых слов Nm, m = 1,..., M, при котором выполняется неравенство (3).
Вернемся к нашему примеру и проверим выполняемость неравенства Крафта. Имеем 2-2 + 2-2 + 2-3 + 2-3 + 2-3 + 2-3 + 2-4 > 1, т. е. префиксный код не может быть построен. Изменим условие, рассмотрим соотношение длин кодовых слов: 2, 2, 3, 3, 3, 4, 4; имеем 2-2 + 2-2 +2-3 + 2-3 + 2-4 + 2-4 = 1; неравенство Крафта выполняется, может быть построен префиксный код (равенство 1 означает, что данный код не может быть улучшен). Метод приоритетного кодирования, учитывающий задаваемое соотношение длин кодовых слов, отражающее приоритетность абонентов системы, основывается на следующих положениях:
· кодирование приоритетов абонентов начинается с младшего разряда с переходом к более старшему разряду кодового слова;
· анализируемому разряду кода приоритета с меньшей заданной длиной кодового слова присваивается значение 1 (более приоритетное значение для арбитража требований ресурса), с большей длиной кодового слова — значение 0;
· при кодировании учитывается, что Q абонентов с равной заданной длиной кода приоритетов при кодировании должны различаться в [logD Q] старших разрядах кодового слова, где [а] — большее целое числа а.
Применение метода для получения кода ОП абонентов для рассмотренного выше примера проиллюстрировано на рис. б.

Рис. 6. Пример приоритетного кода ОП абонентов
* * *
В заключение отметим, что в данной статье рассмотрены альтернативные подходы к построению статических кодов ОП абонентов. Однако предложенный подход позволяет обслуживать заявки в реальном времени при условии изменения приоритетов в процессе функционирования системы по расписанию. Поэтому говорить об оптимальном кодировании возможно только в том случае, если реализуются и оптимальные правила смены кодов приоритетов в процессе функционирования системы.
Список литературы
1. Щеглов А. Ю. Принципы обслуживания заявок в вычислительных системах с динамическими относительными приоритетами // Информационные технологии. 1997. № 8. С. 17—21.
2. Щеглов А. Ю. Принципы унификации методов кодового управления множественным доступом к ресурсам вычислительных систем и ЛВС // Информационные технологии. 1998. № 2. С. 20-26.
3. Щеглов А. Ю. Способы реализации работоспособного синхронного множественного доступа // Электронное моделирование. 1994. Т. 16, № 3. С. 32-38.
4. Щеглов А. Ю. Ускоренное зондирование канала данных — новый принцип случайного доступа в локальных вычислительных сетях // Изв. РАН. Техническая кибернетика. 1994. № 2. С. 129-136.
5. Щеглов А. Ю. Интервальный метод доступа с абсолютной синхронизацией абонентов системы // Электронное моделирование. 1993. Т. 15, № 5. С. 93—94.
6. Щеглов А. Ю. Элементы теории управления множественным доступом пользователей к общим ресурсам вычислительной системы // Вторая Международная конференция "Развитие и применение открытых систем". Тез. докл. М.: Совет РАН по автоматизации научных исследований, 1995. С. 74—76.
7. Щеглов А. Ю. Ускоренный метод децентрализованного кодового управления доступом к моноканалу в реальном времени // Электронное моделирование. 1993. Т. 15, № 3. С. 88—92.
8. Щеглов А. Ю. Высокопроизводительный интервальный метод множественного доступа с естественной синхронизацией абонентов системы // Электронное моделирование. 1993. Т. 15, № 2. С. 93-95.
9. Щеглов А. Ю. Высокопроизводительный метод децентрализованного кодового управления для неоднородной микропроцессорной системы // Кибернетика и системный анализ. 1994. № 2. С. 176-180.
10. Щеглов А. Ю. Счетно-интервальный способ множественного доступа для ЛВС реального времени // Автоматика и вычислительная техника. 1991. № 5. С. 74—77.
11. Щеглов А. Ю. Алгоритм динамического изменения приоритетов для высокопроизводительного метода ДКУ реального времени // Кибернетика и системный анализ. 1994. № 5. С. 179-181.
12. Щеглов А. Ю. Метод синтеза расписаний обслуживания заявок для распределенных вычислительных систем и ЛВС реального времени // Информационные технологии. 1997. № 10. С. 22-27.
13. Колесник В. Д., Полтырев Г. Ш. Курс теории информации. М.: Наука, 1982. 416 с.
14.Владимиров Н. А. Технология ATM: основные положения //Сети. 1996. № 2. С. 62-73.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 5, 1999
Ключевые слова: Вычислительная система, реальное время, относительные приоритеты, оптимальное кодирование, управление множественным доступом, параметрическая оптимизация.
Публикации с ключевыми словами: Вычислительная система, реальное время, относительные приоритеты, оптимальное кодирование, управление множественным доступом, параметрическая оптимизация
Публикации со словами: Вычислительная система, реальное время, относительные приоритеты, оптимальное кодирование, управление множественным доступом, параметрическая оптимизация
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



