научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2013
DOI: 10.7463/0513.0571127
УДК.519.6
Россия, Физический институт им. П.Н. Лебедева РАН (ФИАН). Астрокосмический центр
Россия, Институт машиноведения им. А.А. Благонравова РАН (ИМАШ РАН)
Введение
Работа является третьей в серии из четырех публикаций, посвященных синтезу механизмов ориентации космического телескопа «Миллиметрон» [1, 2].
В последние годы ведется большая работа по синтезу и анализу устройств параллельной структуры. Их первым применением были тренажеры для летчиков. В настоящее время эти устройства применяют в качестве технологических (рисунок 3.1а), манипулирующих, испытательных, измерительных, медицинских (рисунок 3.1б), а также в качестве устройств, для ориентации антенн (рисунок 3.1в). Имеются проекты использования данных устройств для космических применений (рисунок 3.2) [3].
На рисунке 3.2 представлены механизмы, предназначенные для использования в космосе и имеющие параллельно последовательную структуру. Это могут быть обычные (рисунок 3.2а) или сотовые (рисунок 3.2б) конструкции. Каждый модуль может иметь по шесть степеней свободы (рисунок 3.2в). Следует отметить, что в Институте машиноведения им. А.А. Благонравова РАН еще в 80-х годах был создан подобный механизм с 18 степенями свободы («Рука Колискора»)


а) б)

в)
Рисунок 3.1 – Примеры устройств параллельной структуры для технологических (а), манипулирующих, испытательных, измерительных и медицинских (б) применений, а также для ориентации антенн (в)

а)

б)

в)
Рисунок 3.2 – Примеры устройств параллельной структуры для космических применений
Механизмы параллельной структуры характеризуются высокими функциональными свойствами ввиду их высокой точности, грузоподъемности, наличия возможности установить приводы на основании [3, 4]. Эти свойства весьма важны для задачи разработки системы наведения космического радиотелескопа.
В Институте машиноведения ранее разработаны схемы механизмов параллельной структуры для решения широко круга технических задач [5-7], в частности, для манипулирования моделями аэрокосмических систем в аэродинамической трубе, для сверхточного манипулирования в вакууме (рисунок 3.3), для технологических и измерительных систем (рисунок 3.4).

Рисунок 3.3 – Механизм параллельной структуры для сверхточного манипулирования в вакууме

Рисунок 3.4 – Механизм параллельной структуры для технологических и измерительных систем
Важные аспекты анализа данных систем рассмотрены рядом авторов в работах [9-13].
3.1. Методика структурного синтеза параллельных механизмов
Приведем методику структурного синтеза параллельных механизмов на примере механизма с четырьмя степенями свободы (рисунок 3.5), а затем обобщим ее на механизмы с пятью и шестью степенями свободы.

Рисунок 3.5 – Структура механизма четырьмя степенями свободы
В рассматриваемом механизме вращательные кинематические пары, связывающие промежуточные звенья с выходным звеном (его центр обозначен ![]() ), дают статическую неопределимость механизму, превращая его в ферму. Поэтому они заменены на сферические
), дают статическую неопределимость механизму, превращая его в ферму. Поэтому они заменены на сферические ![]() . Кроме того, применены вращательные кинематические пары
. Кроме того, применены вращательные кинематические пары ![]() . Вращательные движения начальных звеньев данного механизма с угловыми скоростями
. Вращательные движения начальных звеньев данного механизма с угловыми скоростями ![]() обеспечиваются соответствующими двигателями. Определим число степеней свободы механизма по формуле Сомова-Малышева:
обеспечиваются соответствующими двигателями. Определим число степеней свободы механизма по формуле Сомова-Малышева:
![]()
![]()
Здесь ![]() ‑ числа одно-, двух-,…,.пяти-подвижных кинематических пар механизма, соответственно.
‑ числа одно-, двух-,…,.пяти-подвижных кинематических пар механизма, соответственно.
Таким образом, мы получили механизм с четырьмя степенями свободы, у которого при отсутствии избыточных связей имеется три вращательных движения и одно поступательное.
Для того, чтобы расположить все приводы механизма на основании (включая вращательные), мы вводим еще два элемента в каждую кинематическую цепь ‑ зубчатое зацепление и поступательную кинематическую пару, сопряженную с одним из зубчатых колес (рисунок 3.6).
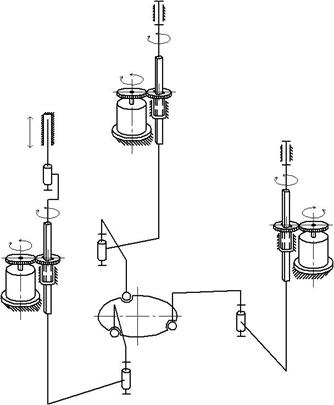
Рисунок 3.6 – Модификация механизма с четырьмя степенями свободы
При проектировании схем механизмов с пятью и шестью степенями свободы можно поступить аналогичным образом.
3.2. Поворот антенны телескопа с помощью механизма параллельной структуры
Рассмотрим задачу по осуществлению поворота антенны телескопа с обеспечением сохранения неизменным положения его центра масс. Для определенности этот поворот будем рассматривать против хода часовой стрелки.
Для поворота фокальной оси антенны телескопа из вертикального положения в горизонтальное, одно из звеньев механизма, жестко связанное с антенной, должно иметь возможность совершать плоское движение в вертикальной плоскости. Это означает, что данное выходное (функциональное) звено механизма должно обладать тремя степенями свободы. То есть, вполне достаточно, чтобы две концевые точки (два шарнира) функционального звена или один из его шарниров при постоянном положении другого шарнира, могли бы изменять свои координаты в плоскости. Таким образом, достаточно использовать плоский механизм с тремя степенями свободы. В соответствии со структурной формулой наиболее простым механизмом этого типа является плоский шестизвенный механизм с тремя степенями свободы (рисунок 3.7).
Рассмотрим задачу синтеза плоского шестизвенного механизма с тремя степенями свободы для осуществления поворота его выходного звена на заданный угол. Ограничимся механизмами с вращательными парами.
Традиционно синтез механизмов проводится в несколько этапов, первым из которых является структурный синтез [14], то есть определение всех возможных схем плоских рычажных шестизвенных механизмов с тремя степенями свободы, пригодных к использованию их по заданному функциональному назначению.

Рисунок 3.7 ‑ Плоский шестизвенный механизм с тремя степенями свободы: ЦМТ – цент масс телескопа; ![]() ‑ шарниры стоек
‑ шарниры стоек
Все плоские шестизвенные механизмы с тремя степенями свободы и одноподвижными вращательными парами можно получить из анализа всех шестизвенных замкнутых кинематических цепей. Ограничимся только двухопорными кинематическими цепями. Таких цепей, состоящих из пяти подвижных звеньев (![]() =5) и шести вращательных пар (
=5) и шести вращательных пар (![]()
![]() =6), можно образовать всего две [14]. Эти шестизвенные замкнутые кинематические цепи могут рассматриваться в качестве “кандидатов” для синтеза шестизвенных механизмов с тремя степенями свободы.
=6), можно образовать всего две [14]. Эти шестизвенные замкнутые кинематические цепи могут рассматриваться в качестве “кандидатов” для синтеза шестизвенных механизмов с тремя степенями свободы.
Шестизвенные механизмы с тремя степенями свободы могут быть построены либо на основе одного кривошип, одного коромысла и одного двойного маятника, либо на основе одного тройного маятника (рисунок 3.7). В первом случае к ведущему звену 1 и двойному маятнику с ведущими звеньями 5 и 4 присоединена структурная группа Ассура второго класса первого вида со звеньями 2 и 3. Во втором случае к тройному маятнику, состоящему из ведущих звеньев 5, 4 и 3, присоединена структурная группа Ассура со звеньями 2 и 1.
Как следует из рисунка 3.7, звено 3 представляет собой совокупность криоконтейнера, имеющего вид прямоугольника с основанием ![]() и высотой
и высотой ![]() , и антенны телескопа радиусом
, и антенны телескопа радиусом ![]() . На рисунке 3.7 также указан размер
. На рисунке 3.7 также указан размер ![]() , определяющий горизонтальное положение звена 3. Величина
, определяющий горизонтальное положение звена 3. Величина ![]() выбирается из конструктивных соображений.
выбирается из конструктивных соображений.
Для определения координат центров шарниров механизма введем систему координат ![]() с началом в центре шарнира
с началом в центре шарнира ![]() на левой опоре (рисунок 3.8).
на левой опоре (рисунок 3.8).

Рисунок 3.8 – Расчетная схема плоского шестизвенного механизма с тремя степенями свободы
На втором этапе синтеза необходимо по заданным условиям определить размеры звеньев механизма, предназначенного для поворота звена 3 из его верхнего крайнего (горизонтального) положения в крайнее нижнее (вертикальное).
Для выполнения основного назначения рассматриваемый механизм должен удовлетворять следующим условиям.
1) Для осуществления свободного поворота антенны телескопа, в крайнем вертикальном положении выходного звена 3 должен быть некоторый зазор ![]() между опорной линией
между опорной линией ![]() и точкой
и точкой ![]() (рисунки 3.7, 3.8). Другими словами, траектория точки
(рисунки 3.7, 3.8). Другими словами, траектория точки ![]() не должна пересекаться с опорной линией
не должна пересекаться с опорной линией ![]() .
.
2) Движения звеньев рассматриваемого механизма должны происходить выше опорной линии ![]() , то есть координаты центров шарниров
, то есть координаты центров шарниров ![]() и
и ![]() должны быть только положительными (
должны быть только положительными (![]() >0,
>0, ![]() >0).
>0).
Остановимся на схеме механизма, представленной на рисунке 3.8, для которой двигатели ведущих звеньев могут быть установлены на основании.
Из конструктивных соображений положение механизма определяется следующими величинами: координаты ![]() центров шарниров
центров шарниров ![]() ,
, ![]() ; расстояние между точками
; расстояние между точками ![]() , т.е. длина
, т.е. длина ![]() =
=![]() звена 6; расстояние между точками
звена 6; расстояние между точками ![]() , т.е. длина
, т.е. длина ![]() выходного звена 3; максимальный угол поворота звена 3, равный 90º; параметры
выходного звена 3; максимальный угол поворота звена 3, равный 90º; параметры ![]() ,
, ![]() .
.
Задача синтеза схемы механизма состоит в том, чтобы на основе исходного положения механизма, определяемого величинами
![]() ,
,
построить его некоторое другое допустимое положение при иных значениях ![]() . Назовем это положение «рабочим.
. Назовем это положение «рабочим.
Как для исходного, так и для рабочего положений механизма необходимо определить длины звеньев ![]() и углы их поворота
и углы их поворота ![]() ;
; ![]() . С этой целью структурную цепь механизма разбиваем на две части: цепь
. С этой целью структурную цепь механизма разбиваем на две части: цепь ![]() , представляющую собой механизм двойного маятника; цепь
, представляющую собой механизм двойного маятника; цепь ![]() , которая является двухкоромысловым механизмом.
, которая является двухкоромысловым механизмом.
3.2.1. Механизм двойного маятника
Рассмотрим рабочее положение механизма в тот момент, когда осуществлен поворот звена 3 на максимальный угол в 90º. Тогда для выполнения условия 1 координата центра шарнира ![]() определяется из соотношения
определяется из соотношения
![]() , (3.1)
, (3.1)
где ![]() =0,02 ‑ 0,05 м.
=0,02 ‑ 0,05 м.
С другой стороны, в этом же положении звена 3 координату ![]() можно представить в виде
можно представить в виде
![]()
![]() , (3.2)
, (3.2)
откуда следует, что
![]() . (3.2a)
. (3.2a)
Из (3.2) видно, что положение центра шарнира ![]() двойного маятника определяется длинами ведущих звеньев
двойного маятника определяется длинами ведущих звеньев ![]() и
и ![]() , а также обобщенными координатами
, а также обобщенными координатами ![]() ,
, ![]() . Для нахождения этих четырех неизвестных следует рассмотреть заданное положение двойного маятника при
. Для нахождения этих четырех неизвестных следует рассмотреть заданное положение двойного маятника при ![]() . Поскольку число неизвестных параметров превышает число уравнений, необходимо задаться некоторыми размерами. В нашем случае удобно задавать длину ведущего звена
. Поскольку число неизвестных параметров превышает число уравнений, необходимо задаться некоторыми размерами. В нашем случае удобно задавать длину ведущего звена ![]() и угол его поворота
и угол его поворота ![]() .
.
Для рационального выбора длин звеньев ![]() ,
, ![]() необходимо определить положение центра шарнира
необходимо определить положение центра шарнира ![]() с координатой, удовлетворяющей соотношению (3.1). С этой целью при различных значениях величины
с координатой, удовлетворяющей соотношению (3.1). С этой целью при различных значениях величины ![]() осуществляем построение траекторий точки
осуществляем построение траекторий точки ![]() . При этом величина
. При этом величина ![]() примет максимальное значение, определяемое равенством
примет максимальное значение, определяемое равенством
![]() , (3.3)
, (3.3)
при ![]() =0.
=0.
Траектория точки ![]() получается в виде дуги окружности радиуса
получается в виде дуги окружности радиуса ![]() с центром в точке
с центром в точке ![]() и располагается на максимальном удалении от точки
и располагается на максимальном удалении от точки ![]() , когда ведущее звено 5 занимает положение, соответствующее
, когда ведущее звено 5 занимает положение, соответствующее ![]() =90°. Серия из полученных таким образом траекторий точки
=90°. Серия из полученных таким образом траекторий точки ![]() для нескольких величин
для нескольких величин ![]() позволяет выбрать искомое положение точки
позволяет выбрать искомое положение точки ![]() . Тем самым удается определить значения длин звеньев
. Тем самым удается определить значения длин звеньев ![]() , а также соответствующие углы ведущих звеньев
, а также соответствующие углы ведущих звеньев ![]() =90,
=90, ![]() , при которых координата центра шарнира
, при которых координата центра шарнира ![]() для искомого рабочего положения механизма будет удовлетворять соотношению (3.1). Следует обратить внимание на то, что значение величины
для искомого рабочего положения механизма будет удовлетворять соотношению (3.1). Следует обратить внимание на то, что значение величины ![]() , полученное из графического построения, можно уточнить по формуле (3.2а).
, полученное из графического построения, можно уточнить по формуле (3.2а).
3.2.2. Двухкоромысловый механизм
Перейдем к рассмотрению двухкоромыслового механизма с двумя опорными точками ![]() и
и ![]() . В начальном рабочем положении коромысло 3 находится в горизонтальном положении и
. В начальном рабочем положении коромысло 3 находится в горизонтальном положении и ![]() . Кроме того, известны длина выходного звена
. Кроме того, известны длина выходного звена ![]() и максимальный угол его поворота в 90º. Из графического построения находим межосевые расстояния
и максимальный угол его поворота в 90º. Из графического построения находим межосевые расстояния ![]() ,
, ![]() . Необходимо определить длины звеньев
. Необходимо определить длины звеньев ![]() ,
, ![]() , а также значения углов поворота
, а также значения углов поворота ![]() ,
, ![]() ведущего звена 1 в начальном и конечном рабочих положениях, соответствующих горизонтальному и вертикальному положениям выходного звена 3.
ведущего звена 1 в начальном и конечном рабочих положениях, соответствующих горизонтальному и вертикальному положениям выходного звена 3.
Следует обратить внимание на то, что в двухкоромысловом механизме точка ![]() движется по дуге окружности радиуса
движется по дуге окружности радиуса ![]() с неподвижным центром в точке
с неподвижным центром в точке ![]() , причем точка
, причем точка ![]() перемещается по ее нисходящей ветви траектории, находящейся в пределах от 180º до 270º по углу поворота звена 3. При этом точка
перемещается по ее нисходящей ветви траектории, находящейся в пределах от 180º до 270º по углу поворота звена 3. При этом точка ![]() должна двигаться по дуге окружности радиуса
должна двигаться по дуге окружности радиуса ![]() с центром в точке
с центром в точке ![]() также по ее нисходящей ветви траектории, находящейся в пределах от 90º до 0º по углу поворота ведущего звена 1.
также по ее нисходящей ветви траектории, находящейся в пределах от 90º до 0º по углу поворота ведущего звена 1.
Для определения неизвестных величин длин звеньев ![]() и
и ![]() следует рассмотреть двухкоромысловый механизм в двух крайних положениях звена 3.
следует рассмотреть двухкоромысловый механизм в двух крайних положениях звена 3.
Сначала рассматриваем вертикальное положение звена 3, в котором координата ![]() очки
очки ![]() равна
равна
![]() . (3.4)
. (3.4)
Для удовлетворения указанному выше условию 2, по которому точка ![]() должна находиться выше опорной линии
должна находиться выше опорной линии ![]() , должно выполняться равенство
, должно выполняться равенство
![]() . (3.5)
. (3.5)
Из равенства (3.5) с учетом (3.4) определяем длину ![]() звена 2. При этом величину
звена 2. При этом величину ![]() принимаем равной 0,05 ‑ 0,10 м.
принимаем равной 0,05 ‑ 0,10 м.
Далее, рассматривая механизм при горизонтальном положении звена 3, можно определить длину ![]() ведущего звена 1 из соотношения
ведущего звена 1 из соотношения
![]() .
.![]() (3.6)
(3.6)
В выражении (3.6) величина ![]() выбирается в зависимости от значения абсциссы точки
выбирается в зависимости от значения абсциссы точки ![]() . Если ее значение находится в отрицательной области, то полагаем
. Если ее значение находится в отрицательной области, то полагаем ![]() =(0,05 ‑ 0,15) м; в противном случае полагаем
=(0,05 ‑ 0,15) м; в противном случае полагаем ![]() =0. В первом случае пересечение окружностей радиусов
=0. В первом случае пересечение окружностей радиусов ![]() ,
, ![]() , вычисленных по соотношениям (3.5) и (3.6), происходит в двух точках, и выбирается та из них, которая находится на нисходящей ветви траектории точки
, вычисленных по соотношениям (3.5) и (3.6), происходит в двух точках, и выбирается та из них, которая находится на нисходящей ветви траектории точки ![]() . Во втором случае указанные окружности имеют точку касания, принадлежащую нисходящей ветви траектории точки
. Во втором случае указанные окружности имеют точку касания, принадлежащую нисходящей ветви траектории точки ![]() .
.
Итак, определив длины звеньев ![]() ,
, ![]() и найдя точки пересечения окружностей радиусов
и найдя точки пересечения окружностей радиусов ![]() и
и ![]() в крайних положениях звена 3 двухкоромыслового механизма, получим на нисходящей ветви траектории точки
в крайних положениях звена 3 двухкоромыслового механизма, получим на нисходящей ветви траектории точки ![]() соответствующие положения ведущего звена 1 и углы его поворота
соответствующие положения ведущего звена 1 и углы его поворота ![]() и
и ![]() .
.
В качестве примера на рисунке 3.8 построены планы рассматриваемого шестизвенного механизма с тремя степенями свободы для начального положения механизма, а также для его конечного рабочего положения, соответствующего повороту выходного звена 3 на угол, равный 90º. При этом принято, что R=4,9 м, ![]() =3,7 м,
=3,7 м, ![]() =3 м,
=3 м, ![]() =0,7 м.
=0,7 м.
В результате синтеза плоского шестизвенного механизма с тремя степенями свободы были получены следующие значения неизвестных величин:
![]() =3,275 м,
=3,275 м, ![]() =3,35 м,
=3,35 м, ![]() =4,325 м,
=4,325 м, ![]() =2,25 м,
=2,25 м, ![]() =6,45 м,
=6,45 м,
![]() =88º,
=88º, ![]() =5,5º,
=5,5º, ![]() =101º,
=101º, ![]() =90º.
=90º.
3.3. Сохранение неподвижным центра масс
Как отмечалось выше, для поворота антенны телескопа относительно космического аппарата целесообразно использовать механизм параллельной структуры с тремя степенями свободы (рисунок 3.9а). Механизм состоит из основания, на котором расположены точки ![]() (точки
(точки ![]() совпадают), подвижной платформы, на которой расположены точки
совпадают), подвижной платформы, на которой расположены точки ![]() (точки
(точки ![]() совпадают), а также трех кинематических цепей
совпадают), а также трех кинематических цепей ![]() . После поворота механизм занимает иное положение (рисунок 3.9б).
. После поворота механизм занимает иное положение (рисунок 3.9б).
Конструкция должна позволять поворот антенный без соприкосновения с элементами механизма (рисунок 3.10). Использование такого механизма позволит осуществлять поворот антенны с сохранением положения центра масс всей системы.

a)
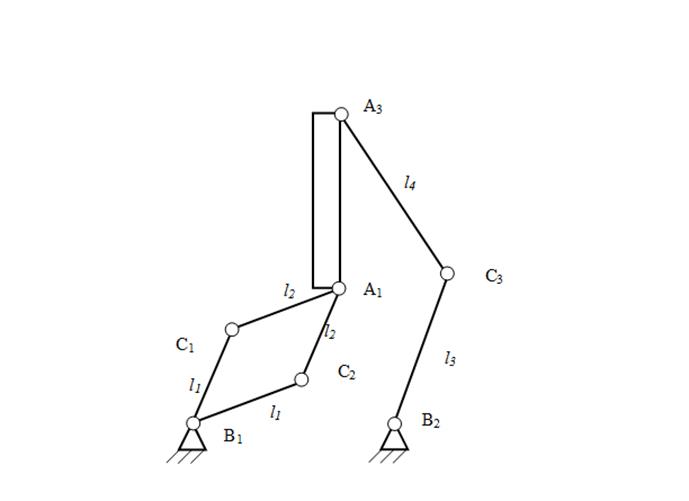
б)
Рисунок 3.9 – Структура параллельного механизма с тремя степенями свободы

Рисунок 3.10 – Механизм параллельной структуры тремя степенями свободы
Выразим координаты точек звеньев механизма при некотором положении выходного звена (платформы). Координаты точки ![]() находим с помощью произведения матриц
находим с помощью произведения матриц
 .
.
Здесь ![]() ‑ координаты центра платформы, φ – угол поворота платформы,
‑ координаты центра платформы, φ – угол поворота платформы, ![]() – координаты точки
– координаты точки ![]() в подвижной системе координат платформы.
в подвижной системе координат платформы.
Используя указанное произведение матриц, получим векторы ![]() , которые представляют собой координаты точки
, которые представляют собой координаты точки ![]() в неподвижной системе координат:
в неподвижной системе координат:
 .
.
Для решения задачи необходимо учесть положения входных звеньев, описываемых углами ![]() , а также координаты центра платформы
, а также координаты центра платформы ![]() и угол поворота платформы вокруг этого центра.
и угол поворота платформы вокруг этого центра.
Запишем координаты точки ![]() , выразив их через угол поворота входного звена:
, выразив их через угол поворота входного звена:
![]() ;
;
![]() .
.
Из этих выражений можно найти величины
![]() ,
, ![]() .
.
Здесь ![]() ‑ угол поворота входного звена (обобщенная координата).
‑ угол поворота входного звена (обобщенная координата).
Выразим длину звена
![]()
и координаты центра масс по оси Х и оси Y
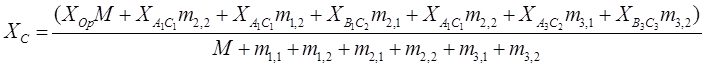 ,
,
 .
.
Здесь M - масса платформы; ![]() ,
, ![]() ‑ координаты центра звена AC;
‑ координаты центра звена AC; ![]() ,
, ![]() ‑ координаты центра звена BC;
‑ координаты центра звена BC; ![]() – масса звеньев.
– масса звеньев.
Пусть заданы координаты точки B, длины и массы звеньев, координаты центра масс антенны. Алгоритм определения координат центра масс антенны при ее повороте имеет следующий вид.
1) Находим координаты точек A1 и A2
![]() ,
,
![]() .
.
2) Определяем расстояние от точки А до точки В
 .
.
3) Вычисляем координаты звеньев АС и ВС
 ,
,  ,
,
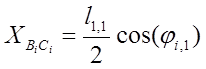 ,
,  .
.
4) По приведенным выше формулам находим координаты центра масс платформы.
Пример. Пусть параметры механизма имеют следующие значения: ![]() =3 м; l2,3=3 м;
=3 м; l2,3=3 м; ![]() =-1,5 м;
=-1,5 м; ![]() =0;
=0; ![]() =1,5 м;
=1,5 м; ![]() =0 м;
=0 м; ![]() =-1,5 м;
=-1,5 м; ![]() =0;
=0; ![]() =1,5 м;
=1,5 м; ![]() =0; M=100 кг; m1,1=5 кг; m1,2=5 кг; m2,1=5 кг; m2,2=5 кг; m3,1=10 кг; m3,2=10 кг; φ=π/6. Зададим координаты положения выходного звена X=0; Y=3 м.
=0; M=100 кг; m1,1=5 кг; m1,2=5 кг; m2,1=5 кг; m2,2=5 кг; m3,1=10 кг; m3,2=10 кг; φ=π/6. Зададим координаты положения выходного звена X=0; Y=3 м.
В ходе вычислений по приведенному выше алгоритму были получены координаты центра масс платформы ![]() =0,063 м;
=0,063 м; ![]() =2,83 м. Выполним коррекцию этих результатов по следующей схеме:
=2,83 м. Выполним коррекцию этих результатов по следующей схеме:
‑ полученное значение координаты ![]() вычитаем из заданного значения этой координаты;
вычитаем из заданного значения этой координаты;
‑ повторяем указанную процедуру до тех пор, пока не будет получена требуемая точность.
В случае, если эта точность составляет 10-6 м, коррекция дает значения координат центра масс ![]() =4,062*10-6 м;
=4,062*10-6 м; ![]() =2,83 м.
=2,83 м.
Заключение
В работе предложен метод синтеза плоских шестизвенных механизмов с тремя степенями свободы с учетом заданных условий, связанных с ориентацией антенны космического телескопа. Особенностью предлагаемого подхода при синтезе таких механизмов является возможность разложить их на два более простых механизма: механизм двойного маятника и двухкоромысловый механизм. Первый механизм с двумя степенями свободы служит для поддержания в постоянном положении точки ![]() , вокруг которой вторым механизмом осуществляется поворот выходного звена на необходимый угол. При этом определяются все неизвестные размеры звеньев и углы их поворота, а также передаточная функция, т.е. зависимость угла поворота выходного звена от угла поворота ведущего звена двухкоромыслового механизма.
, вокруг которой вторым механизмом осуществляется поворот выходного звена на необходимый угол. При этом определяются все неизвестные размеры звеньев и углы их поворота, а также передаточная функция, т.е. зависимость угла поворота выходного звена от угла поворота ведущего звена двухкоромыслового механизма.
Кроме того, рассмотрена задача сохранения неизменного положения центра масс антенны телескопа при изменении ее орентации.
Список литературы
1. Артеменко Ю.Н. Синтез механизмов ориентации космического телескопа «Миллиметрон». 1. Возможности механизмов параллельной структуры для ориентации космического телескопа «Миллиметрон» // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2013. № 1. DOI: 10.7463/0113.0534292
2. Артеменко Ю.Н., Карпенко А.П., Пащенко В.Н., Мартынюк В.А., Волкоморов С.В., Темерев К.А., Шарыгин А.В.. Синтез механизмов ориентации космического телескопа «Миллиметрон». 2. Синтез и оптимизация многосекционного манипулятора параллельной структуры для управления ориентацией космического телескопа «Миллиметрон» // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2013. № 3. DOI:10.7463/0413.0554360
3. Merlet J. P. Parallel robots. Kluwer Academic Publishers, 2000. 372 p.
4. Глазунов В.А., Колискор А.Ш., Крайнев А.Ф. Пространственные механизмы параллельной структуры. М.: Наука, 1991. 96 с.
5. Крайнев А.Ф., Глазунов В.А., Муницына Н.В. Механизмы перемещения заготовки и инструмента для станка нетрадиционной компоновки // СТИН Станки Инструмент. 1995. № 7. С. 10-13.
6. Крайнев А.Ф., Ковалев Л.К., Васецкий Б.Г., Глазунов В.А. Разработка установок для лазерной резки на основе механизмов параллельной структуры // Проблемы машиностроения и надежности машин. 1994. № 1. С. 84-93.
7. Глазунов В.А., Муницына Н.В. Оптимальное проектирование манипуляторов параллельной структуры для агрессивных сред текстильного производства // Известия ВУЗов. Технология текстильной промышленности. 1994. № 5. С. 85-89.
8. Крайнев А.Ф., Глазунов В.А., Муницына Н.В., Рашоян Г.В. Выбор формы упругих элементов кинематических пар механизмов параллельной структуры // Проблемы машиностроения и надежности машин. 1997. № 4. С. 26-35.
9. Ганиев Р.Ф., Кононенко В.О. Колебания твердых тел. М.: Наука, 1976. 432 с.
10. Акопян А.М., Винницкий Е.Я., Крейнин Г.В. К задаче динамического синтеза платформенного механизма с многокоординатным приводом // Проблемы машиностроения и надежности машин. 1990. № 6. С. 78-83.
11. Лунев В.В., Мисюрин С.Ю. Решение задач о положениях механизма методом многоугольников Ньютона // Проблемы машиностроения и надежности машин. 1994. № 2. С. 26-31.
12. Диментберг Ф.М. Движение твердого тела, осуществляемое действием на его точки тяг-толкателей // Машиноведение. 1988. № 5. С. 63-69.
13. Левитский Н.И. Теория механизмов и машин. М.: Наука, 1979. 576 с.
14. Добровольский В.В. Теория механизмов с двумя и более степенями свободы // Труды Станкоинструментального института. 1939. Т. 4. С. 41-76.
Публикации с ключевыми словами: радиотелескоп, космический телескоп «Миллиметрон», механизм параллельной структуры, многосекционный манипулятор
Публикации со словами: радиотелескоп, космический телескоп «Миллиметрон», механизм параллельной структуры, многосекционный манипулятор
Смотри также:
- Синтез механизмов ориентации космического телескопа «Миллиметрон». 2. Синтез и оптимизация многосекционного манипулятора параллельной структуры для управления ориентацией космического телескопа «Миллиметрон»
- Синтез механизмов ориентации космического телескопа «Миллиметрон». 4. Концепция построения интеллектуальной системы активной виброзащиты и высокоточного наведения космического телескопа «Миллиметрон»
- Синтез механизмов ориентации космического телескопа «Миллиметрон». 1. Возможности механизмов параллельной структуры для ориентации космического телескопа «Миллиметрон»
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



