научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#1 январь 2006
В. А. Богатырев, канд. техн. наук, Гос. НИИ "ТЕСТ"
Отказоустойчивость распределенных вычислительных систем динамического распределения запросов и размещение функциональных ресурсов
Рассмотрено динамическое распределение запросов на использование функциональных ресурсов, рассредоточенных по узлам вычислительной системы. Определены рациональные по отказоустойчивости и производительности варианты размещения этих ресурсов по узлам.
Введение. Основным требованием, предъявляемым к распределенным вычислительным системам (РВС), является их отказоустойчивость. Отказоустойчивость РВС обеспечивается как на уровне компьютеров, так и на уровне всей системы. На уровне компьютеров РВС в настоящее время широко внедряется технология избыточных массивов независимых дисков (RAID), а на уровне системы — кластеризация [1, 2]. Для РВС характерно рассредоточение по узлам (компьютерам) задач и функциональных ресурсов (ФР). В связи с ограниченной кратностью резервирования задач и функциональных ресурсов при обеспечении отказоустойчивости РВС должны решаться задачи распределения задач и ФР между компьютерами и их перераспределения в случае возникновения отказов [3—6].
Устойчивость вычислительных систем к отказам процессорных модулей (ПМ) узлов обеспечивается на основе статических и динамических методов перераспределения задач [3, 4], предполагающих после обнаружения отказов ПМ смену задач, возлагаемых на узлы. При реконфигурации возможно использование многовариантности алгоритмов решения задач [6]. Устойчивость РВК к отказам резервированных ФР, рассредоточенных по узлам, а также балансировка загрузки узлов может обеспечиваться в результате динамического распределения запросов через канал связи [7—12].
Отказоустойчивость и производительность РВС зависит от реализации протоколов динамического распределения запросов через канал связи и от варианта размещения ФР по узлам. Выбор рациональных вариантов размещения резервированных ФР по узлам при распределении запросов, каждый из которых требует доступ к одному ФР, рассмотрены в [13, 14]. Не решенной в настоящее время остается задача выбора рациональных вариантов размещения ФР при формировании запросов, каждый из которых требует использования ФР нескольких типов. Решение этой задачи сопряжено с разработкой протоколов динамического распределения, обеспечивающих предпочтительность обслуживания каждого запроса на использование ФР нескольких типов в одном узле, характеризующимся размещением всех затребованных ФР. Такое распределение позволит повысить производительность системы в результате снижения дополнительных издержек на межмашинный обмен. Решению указанной задачи с оценкой достигаемого уровня отказоустойчивости вариантов размещения ФР по узлам посвящена предлагаемая статья.
Постановка задачи. Рассмотрим многомашинную вычислительную систему с шинным каналом связи. Каждый из т узлов содержит ПМ и не более d ФР. Кратность резервирования каждого из n типов ФР будем считать одинаковой и равной r, причем r ≤ m/2. Все r ФР одного типа размещены в разных узлах. Будем считать, что каждый из m узлов содержит оборудование Ω, отказ которого приводит к выходу из строя всего узла (к этому оборудованию относятся, в частности, ПМ) и оборудование ФР, отказ которого связан с потерей только соответствующих функциональных возможностей узла. Условием работоспособности состояний системы является сохранение ФР каждого вида хотя бы в одном узле. Вероятности отказа оборудования Ω для всех узлов предположим одинаковыми и равными pΩ. Вероятности отказа ФР всех видов будем считать совпадающими и равными pf, причем pf ≤ pΩ. События отказа оборудования Ω и ФР как в одном, так и в разных узлах предположим независимыми. Требуется определить рациональные варианты размещения ФР по узлам, когда в процессе решения задачи могут формироваться запросы на доступ к нескольким ФР разного типа.
Динамическое распределение запросов. Рассмотрим реализацию динамического распределения запросов, каждый из которых требует использования ФР нескольких типов. Будем считать, что в каждом узле, формирующем перераспределяемые через канал запросы, отображается размещение по всем узлам работоспособных ФР. В этом случае при формировании запроса определяются узлы размещения затребованных ФР и среди них выбирается единственный узел, предназначенный для обслуживания распределяемого запроса. Если узел с размещением всех затребованных ФР не найден, то обслуживание запроса осуществляется несколькими узлами, содержащими в совокупности все запрашиваемые ФР. После назначения узлов для обслуживания запроса подготавливаются соответствующие протокольные блоки данных (кадры), содержащие информацию, необходимую для передачи и выполнения запроса. Передача адресатам подготовленных протокольных блоков данных запросов осуществляется после предоставления узлу полномочий доступа к каналу.
Выбор рациональных вариантов размещения ФР. В качестве критерия эффективности конфигурации (варианта размещения ФР) выберем:
· B(a) — вероятность обслуживания запроса на использование а ФР в одном узле;
· K — минимальное число отказов компонент, при котором возможен отказ системы. Эффективность конфигурации оценим по показателям [15]:
· P(K) — условная вероятность сохранения работоспособности системы при условии возникновения K отказов;
· Р0(k) — условная вероятность сохранения работоспособности системы при условии возникновения к отказов;
· P(k) — вероятность (безусловная) сохранения работоспособности системы при возникновении к отказов;
·
P — вероятность безотказной работы
системы. Размещение ФР по узлам и состояние РВС охарактеризуем матрицей ||sij||n x m, элемент которой sij
= 1, если j-м узле размещен и исправен ФР r-го типа, в противном случае sij
= 0. Для рассматриваемых вариантов размещения ФР 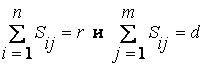 .
.
Рассмотрим два предельных варианта размещения ФР, представленных соответственно матрицами вида S1 и 2.
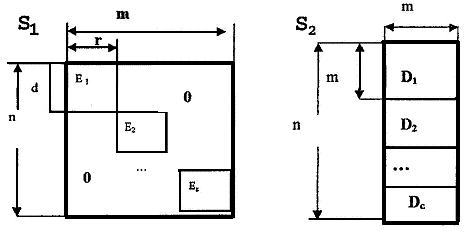
Подматрицы D1, D2,…, Dc имеют вид

Так, при n = m = 6 и r = 4 эти подматрицы имеют вид
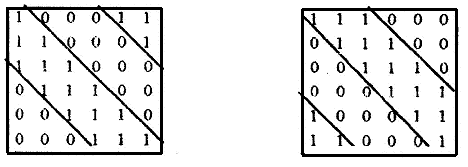
При первом варианте узлы можно разделить на непересекающиеся группы, каждую из которых составляют узлы с одинаковыми функциональными возможностями (с размещением одинаковых типов ФР). Для второго варианта любые два узла различимы по функциональным возможностям.
Следует отметить инвариантность рассматриваемых показателей качества конфигураций к всевозможным перестановкам столбцов и строк матриц S1 и S2 (в связи с чем и даны два эквивалентных варианта представления матриц вида S2). В матрице вида S1 через E1, E2,…, Ez обозначены диагонально расположенные подматрицы, содержащие все единичные элементы. Все элементы матрицы S1, не принадлежащие подматрицам E1, E2,…, Ez, равны нулю. В подматрицах вида D1 D2, ..., Dc через O обозначено подмножество элементов матрицы, равных нулю, а через E — равных единице. В подматрице вида D каждый столбец (или строка), содержащий r единиц, получается сдвигом на один разряд предыдущего столбца. Бинарные матрицы, формируемые подобным образом, называются циркулярными [16].
При заданных значениях d и r число узлов, необходимых для размещения резервированных ФР, находится как m = ent(n/d)r (оператор ent(n/d) означает ближайшее целое, не меньшее n/d). Число подматриц E равно z = ent(n/d), а число подматриц D находится как c = n/m — d/r. Будем считать, что n/d и d/r — целые.
Минимальное число отказов компонент, при котором возможен отказ системы, для сравниваемых конфигураций одинаково и равно r. Для конфигурации, представленной матрицей вида S1 (конфигурация S1), отказ происходит при неисправности r ПМ, соответствующих столбцам расположения подматриц E1, E2,…, Ez. Число комбинаций, удовлетворяющих этому условию при k = r, равно z = n/d = m/r. Для конфигурации вида S2 отказ системы происходит, когда неисправны r ПМ, соответствующие r следующим подряд столбцам. Число комбинаций, удовлетворяющих этому условию при k = r, равно m. Таким образом, условная вероятность сохранения работоспособности системы при возникновении K = r отказов ПМ для конфигураций S1 и S2 соответственно равна

Зависимость условной вероятности сохранения работоспособности системы P(K) от числа узлов m для конфигураций S1 и S2 приведена соответственно кривыми 1 и 2 на рис. 1. Расчет проведен при кратности резервирования ФР r = 4. На графике видна предпочтительность по надежности конфигурации S1, причем она существенна только при небольших m. По мере возрастания m увеличивается влияние на выбор конфигурации ее производительности. Заметим, что конфигурация вида S2 характеризуется большей вероятностью B(a) обслуживания запроса на использование а ФР в одном узле и, следовательно, обладает лучшей производительностью. Вероятность B(a) для конфигурации S1 и S2 определяется соответственно формулами
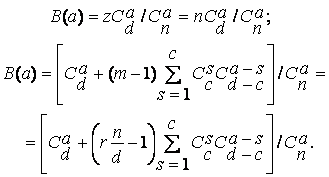
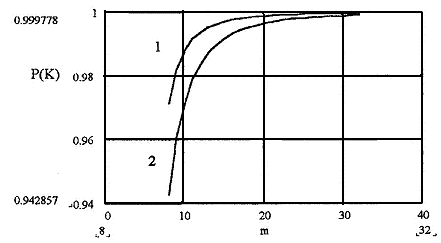
Рис. 1. Зависимость условной вероятности P(K) — сохранения работоспособности системы при условии возникновения K отказов от числа узлов m
В частности, при d = r выполняются соотношения m = n и c = 1,а поэтому для конфигураций, представляемых матрицами и S2, соответственно имеем:
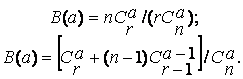
Зависимость вероятности B(a) от числа типов ФР n при d= r = 4 и a = 3,4 для конфигураций S1 и S2 представлена на рис. 2 кривыми 1—2 и 3— 4 соответственно. На рисунке видна предпочтительность по производительности конфигурации, представленной матрицей S2. Эффективность конфигурации, помимо проанализированных показателей производительности, определяется отказоустойчивостью.
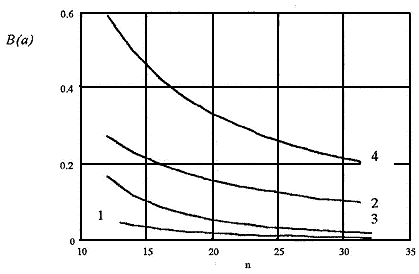
Рис. 2. Зависимость вероятности B(a) обслуживания запроса на использование a ФР в одном узле от числа типов ФР n
Отказоустойчивость конфигурации. Для конфигурации, представленной
матрицей S2, определим условную
вероятность сохранения работоспособности системы при условии возникновения k отказов. Предполагая безотказность ФР, число состояний,
при которых происходит отказ оборудования Ω. (ПМ)
в r и r + b следующих подряд узлах, найдем соответственно как ![]() .
.
Таким образом, используя комбинаторный метод включения—исключения [17],
число устойчивых к отказам к ПМ состояний находится как  . Условная
вероятность сохранения работоспособности системы при возникновении K отказов ПМ и безотказности ФР вычислим как
. Условная
вероятность сохранения работоспособности системы при возникновении K отказов ПМ и безотказности ФР вычислим как
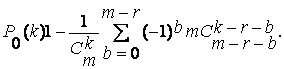
Условная вероятность сохранения работоспособности системы при возникновении k отказов ПМ с учетом ненадежности ФР оценим как
![]()
где Pf(k) — условная вероятность сохранения ФР каждого вида в (m - k) узлах с исправными ПМ при возникновении отказов к ПМ.
При отказе k ПМ число потерянных ФР равно kd, а суммарное число ФР в узлах с исправными ПМ равно (m - k)d, т. е. средняя кратность резервирования ФР узлов с исправным ПМ равна (m - k)d/n.
Таким образом,

где pf — вероятность безотказной работы одного ФР.
Определив условную вероятность P(k) сохранения работоспособности системы при возникновении к отказов ПМ вероятность безотказной работы системы вычисляем как
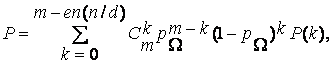
где m - ent(n/d) — максимально возможное число отказов ПМ, выдерживаемых системой.
Для учета ограничений на допустимое при деградации снижение производительности РВС условную вероятность P(k) сохранения работоспособности системы при возникновении к отказов ПМ определим как
![]()
где
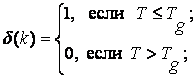
![]() —
предельно допустимое время пребывания в системе запросов на доступ к ФР;
—
предельно допустимое время пребывания в системе запросов на доступ к ФР;
T — среднее время пребывания в системе запросов на доступ к ФР при отказе к ПМ.
Модель, представляющая процесс обслуживания запросов, приведена на рис. 3, на котором система массового обслуживания C0 описывает процесс взаимосвязи (включая распределение запросов) через канал связи (первая фаза обслуживания), а система массового обслуживания С1, С2,.., Cm — процессы обслуживания в узлах размещения ФР (вторая фаза обслуживания). Запрос на использование ФР с вероятностью B(a) обслуживается одним узлом с размещением всех затребованных ФР, а с вероятностью 1 — B(a) — несколькими (a) узлами, содержащими в совокупности все требуемые ФР. При суммарной интенсивности λ0 запросов на использование ФР интенсивность поступления в каждый узел запросов, для выполнения которых достаточно ресурсов узла, Λ = B(a) λ0 /(m - k), а среднее время их обслуживания равно v. Интенсивность поступления в каждый узел запросов, требующих для своего обслуживания ресурсов еще a - 1 узлов, составляет Λ1 = a(1 - B(a)) λ0 /(m - k). Каждый из а задействованных в обслуживании запроса узлов затрачивает на это в среднем время, равное v/a. При обслуживании запроса несколькими узлами следует учитывать дополнительные задержки, связанные с ожиданием доступа к каналу и с обменом информацией между узлами, выполняющими запрос, который требует в среднем время v3.
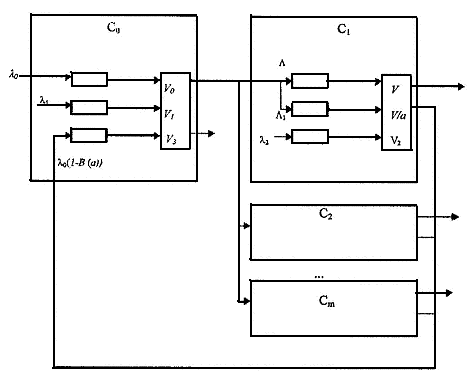
Рис. 3. Модель, представляющая процесс обслуживания запросов на использование ФР
При анализе процесса распределения и обслуживания запросов к ФР следует учитывать фоновую (по отношению к этому процессу) нагрузку канала (C0) и узлов (С1, С2,.., Cm). Будем считать, что интенсивности запросов, составляющих фоновую загрузку канала и каждого узла, равны λ1 и λ2, а среднее время их выполнения равно v1 и v2.
Среднее время пребывания в системе запросов, каждый из которых обслуживается одним узлом, составляет T = W1 + W2 + v0 + v, а несколькими (а) узлами соответственно T = W1 + W2 + v0 + v/a + s, где v0 — среднее время передачи запроса через канал связи; W1 W2 — среднее время ожидания в C0 ив С1, С2,.., Cm; s = W1 + v3 — задержка, связанная с межмашинным обменом при совместном выполнении запроса несколькими узлами.
В простейшем случае, предполагая, что все потоки пуассоновские, время выполнения всех запросов экспоненциально, длины всех очередей неограниченны, а дисциплина их обслуживания бесприоритетна, получим [18]:
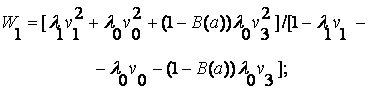
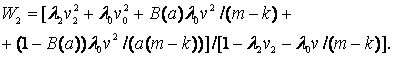
Во время ожидания в очереди системы массового обслуживания С1, С2,.., Cm в принципе возможен отказ затребованных ресурсов, но вероятность этого события мала, а его влияние на среднее время пребывания запросов в системе пренебрежимо. Рассматриваемая модель не учитывает также издержки на диспетчеризацию и, в частности, на реализацию множественного доступа к каналу (включая приоритетный множественный доступ при обслуживании запроса несколькими узлами).
* * *
Таким образом, определены рациональные по производительности и надежности варианты размещения ФР по узлам. Проведена оценка отказоустойчивости и производительности сравниваемых конфигураций при реализации динамического распределения запросов через канал РВС, когда в процессе решения задачи могут формироваться запросы, каждый из которых требует доступ к нескольким ФР разного типа. Полученные результаты могут использоваться при решении задачи размещения ФР по узлам РВС.
Список литературы
1. Росляков Д. И., Терехов И. Ф. Новые технологические решения в построении отказоустойчивых систем // Информационные технологии. 1998, № 1. С. 30—36.
2. Гурвиц М. Безотказные сети и системы // LAN. I998. № 3. С. 121-127.
3. Соловьев А. В., Турута Е. Н. Метод обеспечения отказоустойчивости распределенных систем управления со случайным потоком заявок и статическим распределением задач // Управление ресурсами в интегральных сетях. М.: Наука. 1991. С. 109—116.
4. Турута Е. Н. Организация распределения задач в вычислительных системах, обеспечивающая их отказоустойчивость // Автоматика и вычислительная техника. 1985. № 1. С. 5—14.
5. Киселев В. Д. Метод распределения программ в вычислительных системах с отказами // Электронное моделирование. 1993. Т. 15. № 3. С. 34—37.
6. Харченко В. С, Ильина О. А. Выбор дефектоустойчивой архитектуры вычислительной системы с параллельно-последовательным выполнением задач // Электронное моделирование. 1998. Т. 15. № 2. С. 77-90.
7. Богатырев В. А. К повышению надежности вычислительных систем на основе динамического распределения функций // Изв. вузов. Приборостроение. 1981. С. 62—65.
8. Богатырев В. А. Мультипроцессорные системы с динамическим перераспределением запросов через общую магистраль // Изв. вузов. Приборостроение. 1985. № 3. С. 33—38.
9. Богатырев В. А. Отказоустойчивые многомашинные вычислительные системы динамического распределения запросов при дублировании функциональных ресурсов // Изв. вузов. Приборостроение. 1996. № 4. С. 81—84.
10. Богатырев В. А. Счетно-эстафетный децентрализованный метод динамического распределения запросов в многомашинных вычислительных системах // Автоматика и вычислительная техника. 1993. № 1. С. 10—13.
11. Богатырев В. А. Децентрализованный метод динамического распределения запросов в отказоустойчивых многомашинных вычислительных системах // Автоматика и вычислительная техника. 1993. № 3. С. 73—75.
12. Богатырев В. А. Протоколы динамического перераспределения запросов в распределенных вычислительных системах // Электронное моделирование. 1996. № 3. С. 24—27.
13 .Богатырев В. А. Децентрализованное динамическое распределение запросов в многомашинных вычислительных системах // Электронное моделирование. 1994. Т. 16. № 3. С. 38—43.
14. Богатырев В. А. Надежность вариантов размещения функциональных ресурсов в однородных вычислительных сетях // Электронное моделирование. 1997. № 3. С. 21—29.
15. Черкесов Г. Н. Методы и модели оценки живучести сложных систем. М.: Знание. 1987. 56 с.
16. Тараканов В. Е. Комбинаторные задачи и (0, 1)-матрицы. М.: Наука. 1985. 190 с.
17. Кофман А. Введение в прикладную комбинаторику. М.: Наука. 1975. 480 с.
18. Основы теории вычислительных систем / Под ред. С. А. Майорова. М.: Высш. школа. 1978. 408 с.
ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ, № 5, 1999
ВЫЧИСЛИТЕЛЬНЫЕ СИСТЕМЫ И СЕТИ
Ключевые слова: Распределение работ, размещение ресурсов, отказоустойчивость, реконфигурация трафика, матрица конфигурации.
Публикации с ключевыми словами: Распределение работ, размещение ресурсов, отказоустойчивость, реконфигурация трафика, матрица конфигурации
Публикации со словами: Распределение работ, размещение ресурсов, отказоустойчивость, реконфигурация трафика, матрица конфигурации
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



